Python в анализе данных

Принимать решения без данных это как играть в русскую рулетку: повезет – не повезет. Поэтому данные нужно копить с первого дня жизни бизнеса. Данные это сырье для бизнеса, и по началу они будут помогать принимать решения без особых затрат. Но когда количество данных перевалит за 1 Tb, бизнесу станет сложнее быстро выжимать фичи по векторам на регулярной основе. Помочь может визуализация данных. Имея в багаже математическую базу и возможности Python при использовании библиотек matplotlib, seaborn и plotly, можно покрыть большинство потребностей по визуализации графиков для руководства и для принятия решений.

Существует множество инструментов для визуализации данных: R, Python, JS, Matlab, Scala и Java. R это больше язык для исследователей и студентов, поэтому у него на данный момент больше полезных библиотек для визуализации, чем у Python. Но Python лучше для дальнейшей интеграции разработки.

На больших проектах, где положительные изменения дают 1%<, аналитика необходима. Как минимум, нужно не только проверить результаты a/b теста, но и как эти две группы пользователей вели себя до эксперимента. И отсечь влияние других экспериментов, прошлых и нынешних.

Примерный пайплайн такой:
— проверяем данные на нормальность;
— проверяем отличия с помощью статистического теста;
— доверительным интервалом оцениваем масштаб (среднее при нормальности или медиана для ненормальности данных);
— сравниваем с прошлым поведением групп пользователей;

Данных для визуализации на Python должно быть много, иначе нет смысла в распределенном анализе. Если данных много, то вы почти всегда получите маленькое p-value, и вам останется только проработать нормальность данных, их независимость и т.п. Для расчёт размера выборки нужны тесты для анализа мощности (power tests). На маленьких выборках статистические тесты могут быть менее эффективны, чем экспертная оценка, а на больших данных будут видны даже минимальные отклонение от нормальности. Также, при малой выборке мы не можем использовать центральную предельную теорему.

Основная библиотека для визуализации это Matplotlib. Отмечу, что Matplotlib пусть и очень популярная, но достаточно старая и сложная библиотека, и для комфортной работы лучше использовать API поверх Matplotlib, такие как Seaborn, у которого много своих способов построения графиков. При том, достаточно эстетичных. Достаточно добавить sns.set(), посмотрим на примере:

import matplotlib matplotlib.use('TkAgg') import numpy as np   from matplotlib import pyplot as plt import seaborn as sns; sns.set() norm_data = np.random.normal(size = 1000, loc = 0, scale = 1) plt.hist(norm_data) plt.show()

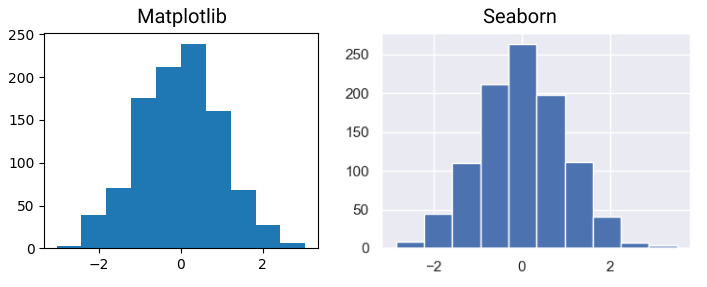
Мы построили наш первый график, используя Python. Конечно, хочется быстрее перейти от работы со списками к работе с массивами значений. Но для начала немного освежим теорию математической статистики:

Нулевая гипотеза всегда консервативна (проще проверяется), а альтернативная гипотеза это ненормальное распределение. В первую очередь проверяется нормальность данных, так как для среднего и стандартного отклонения нормальное распределение может быть лишь одно, ненормальных распределений возможно бесконечное количество. Проверка нормальности возможна тестом Shapiro-Wilk, который проверяет нулевую гипотезу о происхождении данных из нормального распределения.

Стандартное отклонение это квадратный корень дисперсии. Другими словами, это среднее значение квадрата разности значений в наборе данных от среднего значения. Если данные нормально распределены, то нужны среднее и дисперсия. На графиках выше и ниже вы можете видеть примеры визуализации нормального распределения.

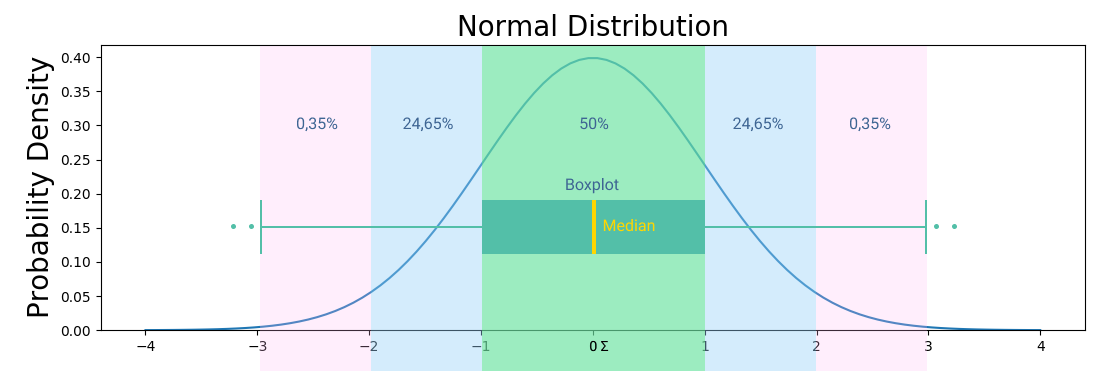
Если не хотим разбираться с нормальным распределением, то используем статистический метод бустрэппинг.

На картинке вы можете видеть центральную линию, это медиана. Помимо удаления выбросов из данных, подсчета размера выборки, кластеризации группы пользователей, обычно всех интересует адекватная мера центральной тенденции, которая может быть представлена следующими понятиями:

• Среднее арифметическое значение в данных. Идея в том, что если взять любое типичное значение из набора данных, оно будет похоже на среднее значение. Не самый надежный способ.
• Медиана. В отличии от среднего арифметического, все значения сортируются в порядке возрастания и в качестве среднего значения берется то, что окажется в середине списка. Считается более надежным подходом. Если в списке четное количество значений, то высчитывается среднее между двумя значениями из центра отсортированного набора данных.
• Мода. Значение, которое можно встретить в данных чаще остальных. Это менее среднее значение, чем два предыдущих. Скорее, это наиболее тяжеловесный фактор, который влияет на среднее значение в данных.

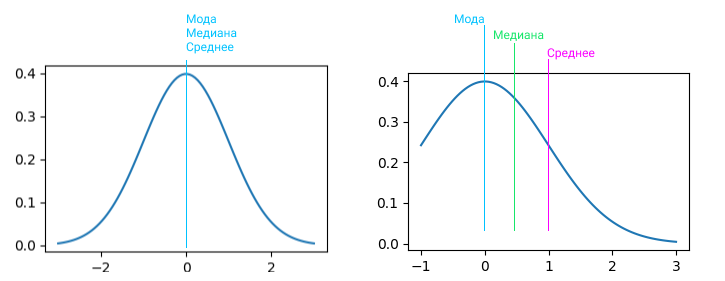
Перейдем к проверке статистической значимости. Допустим, мы выгрузили данные по транзакциям за месяц и хотим понять, были ли отклонения от нормального поведения:

import matplotlib matplotlib.use('TkAgg') import scipy.stats as stats from matplotlib import pyplot   x = stats.norm.rvs(loc=5, scale=3, size=543) print (stats.shapiro(x)) pyplot.hist(x) pyplot.show()

Я осознанно не использую seed, так как чем больше вариативность полученных вами результатов, тем лучше. У меня возвращено 2 значения: значение статистики теста, и связанное с ним значение p-value, в моем случае получилось 0.011658577248454094. А так как 0.0116 < 0.05, и для отклонения нулевой гипотезы p-value должно быть не выше альфы 0,05, то у нас есть веские доказательства того, что мы отвергаем нулевую гипотезу на уровне значимости 0,05.

Но перед тем, как делать вывод об отсутствии различий, мы еще должны выяснить, была ли мощность использованного статистического критерия достаточной для их обнаружения. А мощность упирается в размер выборки. Нельзя сравнивать близкие законы при малых объёмах выборок.

Меняем Критерий Шапиро-Уилка на тест Андерсона, print (stats.anderson(x)), проверяем еще раз, что данные в выборке более менее нормально распределены. За тестом Андерсона Дарлинга часто используют w^2 Мизеса. Результат можно проверить даже визуально:

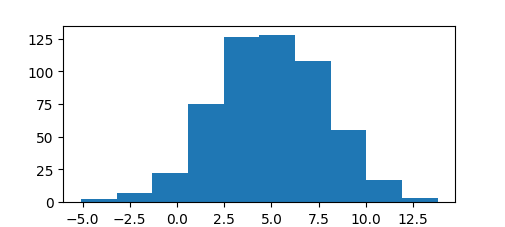
Давайте проведем F-тест, так как настало время проверки статистической значимости различий. Допустим, нужно сравнить работу продажников из двух городов.

Используем для этого ANOVA (дисперсионный анализ) из библиотеки Scipy, командой stats.f_oneway. Нулевая гипотеза ANOVA предполагает, что мат. ожидания совпадают. Если t-критерий Стьюдента используется для сравнения среднего значения в двух независимых группах, то f-критерий проверяет, есть ли вообще разница. Можно использовать для большего количества выборок, чем 2. Разумеется, ANOVA не является f-тестом в полной мере, это модель регрессии и считается обобщенной линейной моделью (GLM). ANOVA используется для сравнения среднего значения какого-то признака в независимых группах.

import matplotlib matplotlib.use('TkAgg') import scipy.stats as stats   a = [2,3,1,4,3,4,2,4,-1,32,12,53,2,2,3,2.3,2,4.2,3,32,1] b = [3,4,-1,3,4,43,4,14,2.3,1,3,2.3,12,42,2.4,3,4,1,4,1,2] print (stats.f_oneway(a,b))

Получаем F-статистику F_onewayResult(statistic=0.0386380063725391, pvalue=0.8451628704190369), что говорит нам, больше ли дисперсия между группами, чем дисперсия внутри групп, и вычисляет вероятность наблюдения этого коэффициента дисперсии, используя F-распределение. Конечно, для научных публикаций данных недостаточно, нет степеней свободы. Но заветный P-value мы получили и теперь знаем, что раз 0.8451628704190369 > 0.05, то работа продажников явно завязана не только на тех данных, что у нас имеются. У нас отказ от нулевой гипотезы, так как данные не выглядят нормально. Нулевая гипотеза a = b, альтернативная a ? b.

Сравним средние двух выборок с помощью T-test. Мы хотим узнать, есть ли различия в двух группах данных, пусть это будут результаты A/B теста для туториалов в мобильном приложении. Для этого нужно интерпретировать статистическое значение в двустороннем тесте с примерно нормальным распределением, что означает, что нулевая гипотеза может быть отвергнута, когда средние значения двух выборок слишком отличаются. В R мы использовали функцию t.test() для простого t-теста Стьюдента, в Python у нас больше возможностей. Можно выполнить как односторонний, так и двусторонний t-test в Python. Если у вас много шума в данных, не забудьте сделать дисперсию. Стьюдента для независимых выборок считают с равными дисперсиями.

У двустороннего теста и p-value получится в два раза больше, чем у одностороннего, поэтому двусторонний тест имеет более строгие критерии для отклонения нулевой гипотезы. Гипотетически, из двустороннего p-value можно получить одностороннее, но при правильно проведенном тесте не должно возникнуть такой необходимости. При двустороннем тесте мы делим p-value 0.05 на два, и отдаем по 0.025 на положительный и отрицательный концы распределения. При одностороннем тесте весь p-value 0.05 располагается в одном конце распределения. Так как второй конец распределения игнорируется, то есть вероятность ошибки: создав новый туториал, можно протестировать односторонним тестом, лучше ли новый туториал предыдущего. Но информация о том, хуже ли новый туториал предыдущего, будет проигнорирована. Но если новый туториал рассчитан на другую аудиторию и мы точно знаем, что он не может быть хуже, то односторонний тест вам подходит и даст бОльшую точность.

Вводные для следующего примера: нулевая гипотеза что мат. ожидания для двух групп равны, дисперсии равны. Данные представляют финансовые результаты двух разных интернет-магазинов схожей тематики.

import matplotlib matplotlib.use('TkAgg') from scipy import stats   a = [742,148,423,424,122,432,-1,232,243,332,213] b = [-1,3,4,2,1,3,2,4,1,2] print (stats.ttest_ind(a,b))

Результаты завязаны на проблеме Беренса-Фишера, так как точного решения не существует, но вероятность позволяет нам сделать вывод. Если сделать поправку на то, что при маленькой выборке никак не сгруппированных данных у нас большая дисперсия (проверяем дисперсию командой print(np.var(a)) ), то качество данных можно поставить под сомнение. Если данные не распределены нормально, нужен критерий Манна-Уитни, также известный как Критерий Уилкоксона. Выборка у нас небольшая, поэтому Манна-Уитни вполне подойдет, ранги не будут сильно пересекаться.

import matplotlib matplotlib.use('TkAgg') from scipy import stats   a = [742, 148, 423, 424, 122, 432, -1, 232, 243, 332, 213] b = [-1, 3, 4, 2, 1, 3, 2, 4, 1, 2]   u, p_value = stats.mannwhitneyu(a, b) print("two-sample wilcoxon-test", p_value)

P-value стал 0.0007438622219910575. Сравнивать выборки можно и визуально:

import matplotlib matplotlib.use('TkAgg') import numpy as np from scipy.stats import ttest_ind import matplotlib.pyplot as plt a = np.random.normal(loc=0,scale=24,size=4454) b = np.random.normal(loc=-1,scale=1,size=7643)   print(ttest_ind(a,b))   plt.hist(a, bins=24, color='g', alpha=0.75) plt.hist(b, bins=24, color='y', alpha=0.55) plt.show()

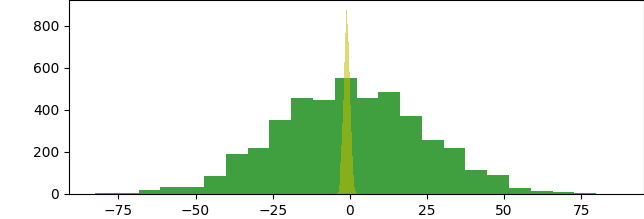
Теперь рассмотрим двусторонний тест для нулевой гипотезы о том, что ожидаемое среднее значение одной выборки независимых наблюдений равно среднему значению другой. Аспект «двусторонний» означает, что мы рассматриваем верхнюю и нижнюю границы распределения совокупности данных. Стандартные отклонения должны быть одинаковыми.

import matplotlib matplotlib.use('TkAgg') from scipy import stats   from scipy import stats a = stats.norm.rvs(loc = 5,scale = 10,size = 23000) b = stats.norm.rvs(loc = 5,scale = 10,size = 23425) print stats.ttest_ind(a,b)

Получаем statistic=-0.7043486133916781, pvalue=0.4812192321148787, что намного больше 0,05. А так как р > 0.05 мы считаем маловероятной ошибкой, а р <= 0.05 высоковероятной, то две выборки можно считать равными. Также, для проверки равенства средних подходят Критерий Манна-Уитни, Уилкоксона, Краскера-Уолласа.

Визуализация

import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np   sns.set() data = np.random.multivariate_normal([0, 0], [[43, 2], [5, 1.2]],size=25000) data = pd.DataFrame(data, columns=['x', 'y'])   for col in 'xy':     sns.kdeplot(data[col], bw=.2, shade=False, label="MAU"), plt.show()

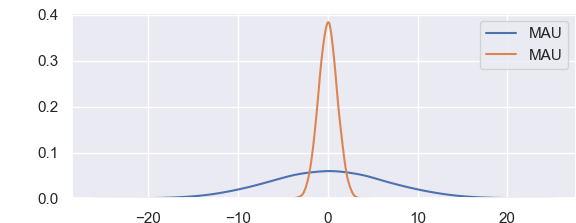
График выше прекрасно подходит для визуального сравнения двух выборок. Доверительный интервал находится между 5 и 95 процентым квантилем, 90% доверительный интервал это двусторонний критерий между 5 и 95.

import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np   plt.style.use('classic') plt.style.use('seaborn-whitegrid') data = np.random.multivariate_normal([0, 0], [[3.4, 1.87], [2.8, 1.44]],size=25000) data = pd.DataFrame(data, columns=['x', 'y']) sns.distplot(data['x']) sns.distplot(data['y']);   plt.show()

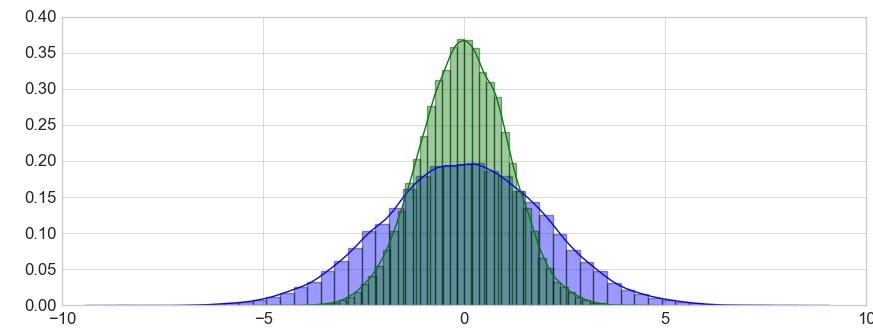
Представленные выше графики достаточно стандартны и вы неоднократно их строили или, по крайней мере, видели. А вот следующий график, Jointplot, уже куда интереснее. Он совмещает в себе гистограммы по x и y, и включает типичный график рассеяния. Получается своеобразный куб из гистограмм.

import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd import numpy as np   plt.style.use('classic') plt.style.use('seaborn-whitegrid') data = np.random.multivariate_normal([0, 0], [[43, 2], [5, 1.2]],size=25000) data = pd.DataFrame(data, columns=['x', 'y']) with sns.axes_style('white'):     sns.jointplot("x", "y", data, kind='kde');   plt.show()

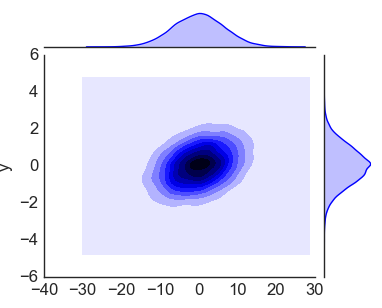
Получилось! Далее построим диаграмму рассеивания.

import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import numpy as np a = np.random.rand(20) b = [3, 4, 3.4, 6, 7, 8, 9, 10, 4, 0.3, 4.2, 4, 23, 3, 33, 3, 1, 4, 0.1, 4.2] colors = np.random.rand(20) plt.scatter(a, b, c=colors, s=100, alpha=0.65, marker=(5, 0)) plt.show()

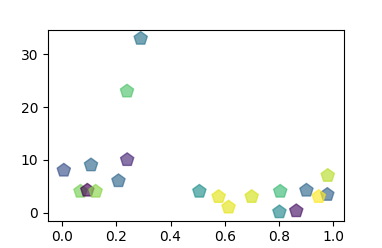
График интересен тем, что полученные рассеивающиеся паттерны позволяют увидеть разные типы корреляции. Стремится с правый верхний угол — хорошая тенденция, расположилось горизонтально — нейтральная тенденция, стремится в левый верхний угол — негативная тенденция.

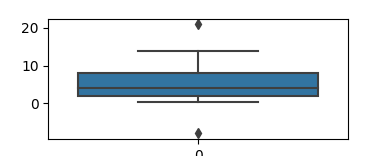
И Box Plot, куда же без него. Работает с группой из минимум пяти чисел: минимум, первый квартиль, медиана, третий квартиль и максимум. Усы идут от каждого квартиля до минимума или максимума.

import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import seaborn as sns import pandas as pd   b = [1, 2, 3, 4, 3.4, 6, 7, 8, 9, 8, 4, 0.3, 4.2, 14, 21, 1, -8] df = pd.DataFrame(b) sns.boxplot(data=df) plt.show()

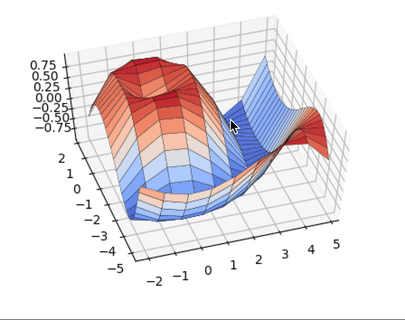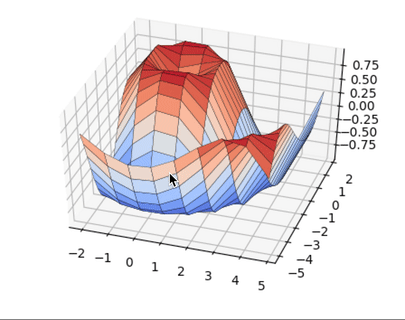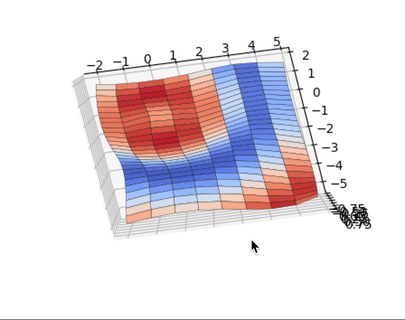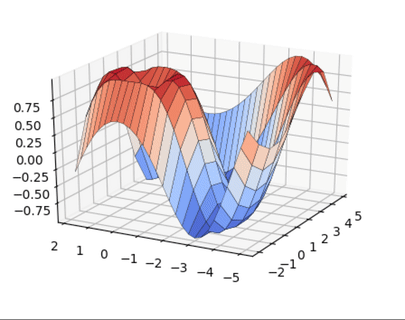
 А теперь немного 3D, бизнес такое любит:

import matplotlib matplotlib.use('TkAgg') import matplotlib.pyplot as plt import numpy as np from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D   x = np.arange(-2, 5, 0.85) xlen = len(x) y = np.arange(-5, 2, 0.25) ylen = len(y) x, y = np.meshgrid(x, y) r = np.sqrt(x**2 + y**2) z = np.sin(r * 1.3)   ax = plt.figure(figsize=(8,6)) ax = ax.add_subplot(1,1,1, projection='3d') ax.plot_surface(x, y, z, cmap=cm.coolwarm, edgecolor='black', linewidth=0.23, antialiased=True)   plt.show()

Python Seaborn это лучшее решение для визуализации привлекательных статистических диаграмм. Если же ваша цель это интерактивные графики в вебе, то Python Bokeh, Pygal, Plotly это ваш выбор. Изучайте Python и мат. стат, и ваш продуктовый дизайн сильно вырастет.

Источник: your-scorpion.ru

Комментарии: