Построение Гистограммы Питона: NumPy, Matplotlib, Pandas & Seaborn
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2019-06-30 16:00

В этом учебном пособии вы будете оснащены, чтобы сделать графики гистограммы Python с качеством производства и готовыми к презентации с различными вариантами и функциями.
Если у вас есть введение в промежуточные знания в Python и статистику, вы можете использовать эту статью как универсальный магазин для создания и построения гистограмм в Python с использованием библиотек из своего научного стека, включая NumPy, Matplotlib, Pandas и Seaborn.
Гистограмма-отличный инструмент для быстрой оценки распределения вероятностей, интуитивно понятного практически любой аудитории. Python предлагает несколько различных вариантов построения и построения гистограмм. Большинство людей знают гистограмму по ее графическому представлению, которое похоже на гистограмму:
Эта статья проведет вас через создание графиков, как выше, а также более сложных. Вот то, что вы будете покрывать:
- Построение гистограмм в чистом Python, без использования сторонних библиотек
- Построение гистограмм с помощью NumPy для суммирования базовых данных
- Построение результирующей гистограммы с помощью Matplotlib, Pandas и Seaborn
Бесплатный бонус: мало времени? Нажмите здесь, чтобы получить доступ к бесплатному двухстраничному чит-листу Python histograms, который суммирует методы, описанные в этом руководстве.
Гистограммы в чистом Python
Когда вы готовитесь к построению гистограммы, проще всего не думать в терминах бункеров, а сообщать, сколько раз появляется каждое значение (таблица частот). Словарь Python хорошо подходит для этой задачи:
>>> # Не должны быть отсортированы, обязательно >>> а = (0, 1, 1, 1, 2, 3, 7, 7, 23) >>> деф count_elements(сл) -> словарь: ... """Элементы подсчета из 'seq'.""- нет ... hist = {} ... ибо я в seq: ... hist [ i] = hist .получаем (i , 0 ) + 1 ... return hist >>>>>> >>> counted = count_elements (a ) >>>>>> >>> подсчитано {0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1} count_elements() возвращает словарь с уникальными элементами из последовательности в качестве ключей и их частотами (счетчиками) в качестве значений. В цикле over seqhist[i] = hist.get(i, 0) + 1говорится: "для каждого элемента последовательности увеличьте его соответствующее значение на hist1.”
Фактически, это именно то, что делает collections.Counterкласс из стандартной библиотеки Python, который подклассы словаря Python и переопределяет его .update()метод:
>>> из коллекции импорт счетчиков >>> пересказала = счетчик(с) >>> рассказал счетчика({0: 1, 1: 3, 3: 1, 2: 1, 7: 2, 23: 1}) Вы можете подтвердить, что ваша функция ручной работы делает практически то же самое, collections.Counterчто и при тестировании на равенство между ними:
>>>>>> >>> пересчитал .items () = = подсчитано .items() True
Техническая деталь: отображение count_elements()сверху по умолчанию для более оптимизированной функции C, если она доступна. В функции Python count_elements()одна микро-оптимизация, которую вы могли бы сделать,-объявить get = hist.getперед циклом for. Это будет привязывать метод к переменной для более быстрых вызовов в цикле.
Это может быть полезно для создания упрощенных функций с нуля в качестве первого шага к пониманию более сложных. Давайте еще немного изобретем колесо с гистограммой ASCII, которая использует преимущества форматирования вывода Python:
def ascii_histogram (seq ) ->> None : """горизонтальный график частотной таблицы/гистограммы.""" counted = count_elements ( seq ) for k in sorted (counted ): print ('{0:5d} {1} ' .формат (k, ' + ' * подсчитано [ k])) Эта функция создает отсортированную частотную диаграмму, где подсчеты представлены как суммы символов plus (+). Вызов sorted()словаря возвращает отсортированный список его ключей, а затем вы получаете доступ к соответствующему значению для каждого counted[k]из них . Чтобы увидеть это в действии, вы можете создать немного больший набор данных с randomмодулем Python:
>>>>>> >>> # Никакого Онемения ... и все же ... >>>>>> >>> импорт случайный >>>>>> >>> Рэндом .семя ( 1 ) >>>>>> >>> vals = [ 1 , 3 , 4 , 6 , 8 , 9 , 10 ] >>>>>> >>> # каждое число в 'vals' будет происходить от 5 до 15 раз. >>>>>> >>> freq = (случайный .randint (5 , 15 ) for _ in vals ) >>>>>> >>> данные = [] >>>>>> >>> для F, v в zip (freq, vals ): ... Дейта .продлить([в] * Ф) >>> ascii_histogram(сведения) 1 +++++++ 3 ++++++++++++++ 4 ++++++ 6 +++++++++ 8 ++++++ 9 ++++++++++++ 10 ++++++++++++
Здесь вы имитируете выщипывание valsс частотами, заданными freq(выражение генератора). Полученная выборка данных повторяет каждое значение от valsопределенного числа раз от 5 до 15.
Примечание: random.seed()используется для заполнения или инициализации базового генератора псевдослучайных чисел (PRNG), используемого random. Это может звучать как оксюморон, но это способ сделать случайные данные воспроизводимыми и детерминированными. То есть, если вы скопируете код здесь как есть, вы должны получить точно такую же гистограмму, потому что первый вызов random.randint()после посева генератора будет производить идентичные “случайные” данные, используя Твистер Мерсенна .
Построение из базы: расчеты гистограммы в NumPy
До сих пор вы работали с так называемыми “частотными таблицами"."Но математически гистограмма-это отображение бункеров (интервалов) на частоты. Более технически, его можно использовать для аппроксимации функции плотности вероятности ( PDF ) базовой переменной.
Переходя от” частотной таблицы “выше, истинная гистограмма сначала” закапывает " диапазон значений, а затем подсчитывает количество значений, которые попадают в каждую ячейку. Это то, что histogram()делает функция NumPy, и это основа для других функций, которые вы увидите здесь позже в библиотеках Python, таких как Matplotlib и Pandas.
Рассмотрим пример поплавков, взятых из распределения Лапласа . Это распределение имеет более толстые хвосты, чем нормальное распределение и имеет два описательных параметра (местоположение и масштаб):
>>>>>> >>> импорт numpy как np >>>>>> >>> # `тупой.random ' использует свой собственный PRNG. >>> np.Рэндом .семя ( 444 ) >>>>>> >>> np .set_printoptions (точность = 3 ) >>>>>> >>> d = np .Рэндом .laplace (loc = 15, масштаб = 3, размер = 500 ) >>>>>> >>> D [: 5 ] массив([18.406, 18.087, 16.004, 16.221, 7.358])
В этом случае вы работаете с непрерывным распределением, и было бы не очень полезно подсчитывать каждый поплавок независимо, вплоть до десятичного знака после запятой. Вместо этого, вы можете bin или “ведро” данные и подсчитать наблюдения, которые попадают в каждую ячейку. Гистограмма-это результирующее количество значений в каждом Бине:
>>>>>> >>> hist, bin_edges = np .гистограмма(д) >>> Хист массива([ 1, 0, 3, 4, 4, 10, 13, 9, 2, 4]) >>> bin_edges массива([ 3.217, 5.199, 7.181, 9.163, 11.145, 13.127, 15.109, 17.091, 19.073, 21.055, 23.037])
Этот результат может быть не сразу интуитивным. np.histogram()по умолчанию используется 10 ячеек одинакового размера и возвращает кортеж счетчиков частоты и соответствующие ребра ячейки. Они являются ребрами в том смысле, что будет еще одно ребро ячейки, чем есть члены гистограммы:
>>>>>> >>> Хист .размер, bin_edges .размер (10, 11)
Техническая деталь: все, кроме последнего (правого) бункера, наполовину открыты. То есть все бункеры, кроме последнего, являются [включающими, исключительными), а последний бункер является [включающим, включающим].
Очень сжатая разбивка того, как бункеры построены NumPy, выглядит так:
>>>>>> >>> # Крайний левый и правый края бункера >>>>>> >>> first_edge, last_edge = a .min(), a.max () >>>>>> >>> n_equal_bins = 10 # NumPy по умолчанию >>>>>> >>> bin_edges = np .linspace (start = first_edge , stop = last_edge , ... num = n_equal_bins + 1, endpoint = True ) ... >>>>>> >>> массив bin_edges ([ 0. , 2.3, 4.6, 6.9, 9.2, 11.5, 13.8, 16.1, 18.4, 20.7, 23. ])
Приведенный выше случай имеет большой смысл: 10 равномерно расположенных бункеров в диапазоне от пика до пика 23 означают интервалы ширины 2.3.
Оттуда функция делегирует либо np.bincount()or np.searchsorted(). bincount()сам по себе может использоваться для эффективного построения "частотной таблицы", с которой вы начали здесь, с отличием, что включены значения с нулевыми вхождениями:
>>> bcounts = np.bincount ( a ) >>>>>> >>> hist, _ = np .гистограмма (a, range = (0, a .max()), bins=a.max() + 1) >>> np.array_equal (hist , bcounts ) True >>>>>> >>> # воспроизведение коллекций.Счетчик` >>>>>> >>> dict (zip (np .уникальный (a ), bcounts [ bcounts .ненулевое значение ()])) {0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1} Примечание: histздесь действительно используются бункеры ширины 1.0, а не” дискретные " отсчеты. Следовательно, это работает только для подсчета целых чисел, а не плавает, например [3.9, 4.1, 4.15].
Визуализация гистограмм с Matplotlib и пандами
Теперь, когда вы увидели, как построить гистограмму в Python с нуля, давайте посмотрим, как другие пакеты Python могут выполнить эту работу за вас. Matplotlib предоставляет функциональные возможности для визуализации гистограмм Python из коробки с универсальной оберткой вокруг Numpy's histogram():
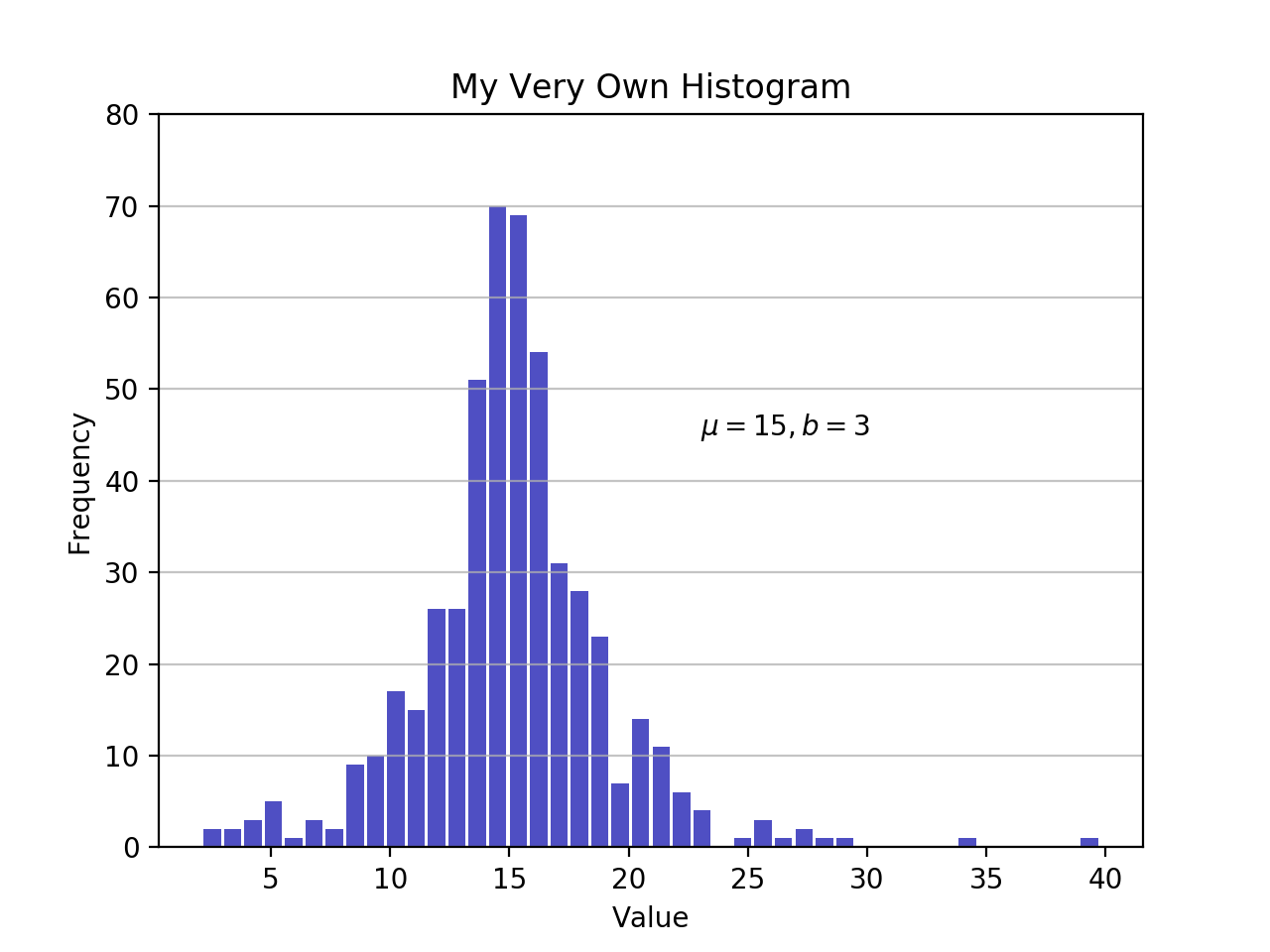
импорт matplotlib.pyplot как plt # an "интерфейс" к matplotlib.ось.Ось.hist () метод n, bins, patches = plt .hist (x = d , bins = 'auto' , color = '#0504aa' , alpha = 0.7 , rwidth = 0.85 ) plt .сетка (ось = 'y' , Альфа = 0.75 ) plt .xlabel ('значение') plt .ylabel ('частота') plt .название ('Моя собственная гистограмма') plt .текст (23, 45, r '$mu=15, b=3$' ) maxfreq = n .max () # установите чистый верхний предел по оси Y. plt.ylim (ymax = np .ceil (maxfreq / 10) * 10 если maxfreq % 10 еще maxfreq + 10) Как определено ранее, график гистограммы использует ребра ячеек на оси x и соответствующие частоты на оси Y. В приведенной выше диаграмме передача bins='auto'выбирает между двумя алгоритмами для оценки "идеального" количества ячеек. На высоком уровне целью алгоритма является выбор ширины ячейки, которая генерирует наиболее точное представление данных. Для получения дополнительной информации по этому вопросу, который может стать довольно техническим, проверьте выбор бункеров гистограммы из документов Astropy.
Оставаясь в научном стеке Python, Pandas Series.histogram() использует matplotlib.pyplot.hist()для рисования гистограммы Matplotlib входного ряда:
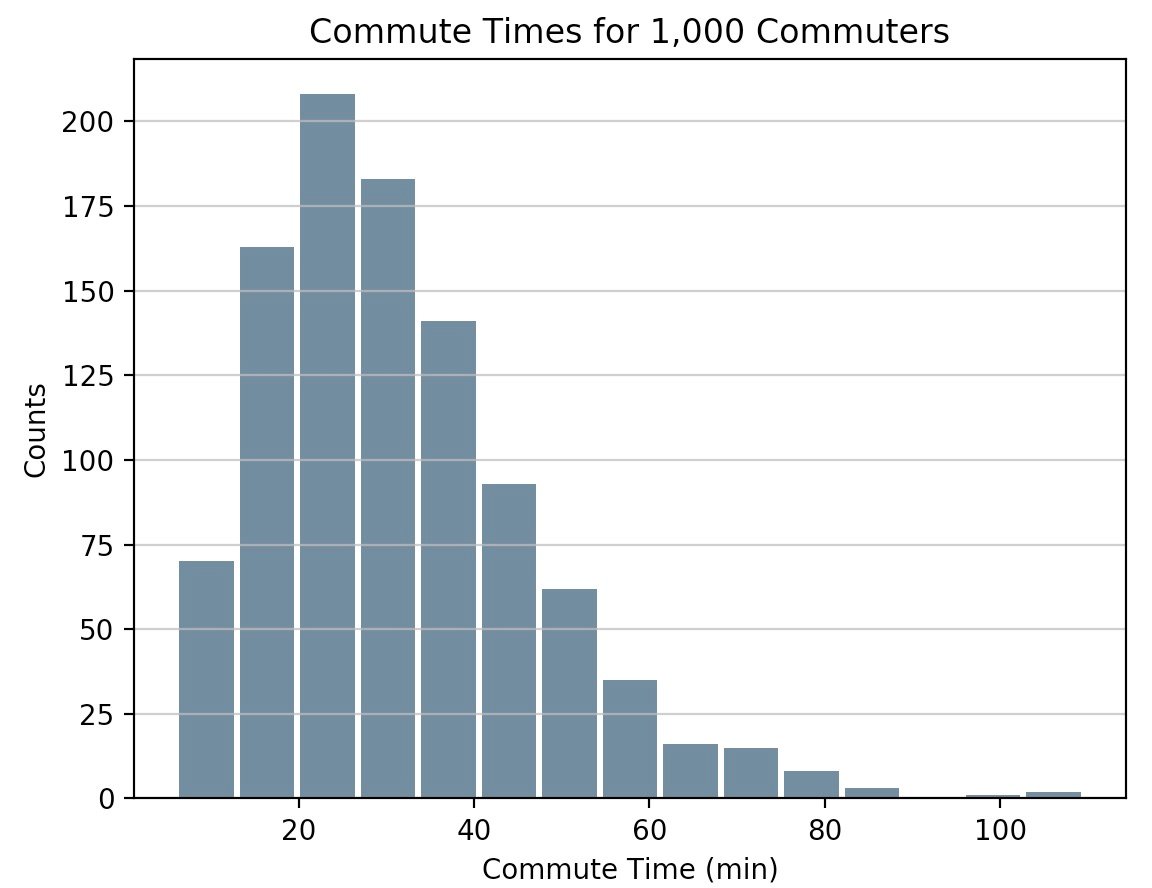
импорт панды как pd # генерировать данные на коммутируют раз. размер, масштаб = 1000, 10 коммутирует = pd .Серия (np .Рэндом .гамма (масштаб , размер = размер) * * 1.5 ) коммутирует .заговор .hist (grid = True , bins = 20 , rwidth = 0.9 , color = '#607c8e' ) plt .название ('коммутируют раз для 1000 пассажиров') plt .xlabel ('графы') plt .ylabel ('коммутируют время') plt .сетка (ось = 'y', Альфа = 0.75) pandas.DataFrame.histogram() аналогично, но создает гистограмму для каждого столбца данных в фрейме данных.
Построение оценки плотности ядра (KDE)
В этом уроке вы работали с образцами, статистически говоря. Независимо от того, являются ли данные дискретными или непрерывными, предполагается, что они получены из совокупности, которая имеет истинное точное распределение, описанное всего несколькими параметрами.
Оценка плотности ядра (KDE) - это способ оценки функции плотности вероятности (PDF) случайной величины, которая “лежит в основе” нашей выборки. KDE - это средство сглаживания данных.
Придерживаясь библиотеки Pandas, вы можете создавать и накладывать графики плотности , используяplot.kde(), который доступен как для объектов, так Seriesи DataFrameдля объектов. Но сначала давайте создадим два различных образца данных для сравнения:
>>>>>> >>> # Пример из двух различных нормальных распределений >>>>>> >>> средство = 10 , 20 >>>>>> >>> stdevs = 4 , 2 >>>>>> >>> dist = pd .DataFrame( ... np.Рэндом .normal ( loc = означает , scale = stdevs , size = (1000 , 2 )), ... columns = ['a', 'b' ]) >>>>>> >>> dist .agg (['min' , 'max' , 'mean', 'std']).круглый (десятичные = 2) A B мин -1.57 12.46 Макс 25.32 26.44 означает 10.12 19.94 std 3.94 1.94
Теперь, чтобы построить каждую гистограмму на одной оси Matplotlib:
рис, ax = plt .subplots() dist.заговор .kde (ax = ax , legend = False , title = 'Histogram: A vs .B' ) dist.заговор .hist (плотность = True , ax = ax ) ax .set_ylabel ('вероятность') ax .сетка (axis = 'y' ) ax .set_facecolor ('#d8dcd6') Эти методы используют Scipy'sgaussian_kde(), что приводит к более плавному PDF-файлу.
Если вы внимательно посмотрите на эту функцию, вы увидите, насколько хорошо она приближается к “истинному” PDF для относительно небольшой выборки из 1000 точек данных. Ниже вы можете сначала построить” аналитическое " распределение scipy.stats.norm(). Это экземпляр класса, который инкапсулирует статистический стандарт нормального распределения, его моменты и описательные функции. Его PDF является “точным” в том смысле, что он точно определен как norm.pdf(x) = exp(-x**2/2) / sqrt(2*pi).
Построив оттуда, вы можете взять случайную выборку из 1000 точек данных из этого дистрибутива, а затем попытаться вернуться к оценке PDF с помощью scipy.stats.gaussian_kde():
из scipy import stats # объект, представляющий" замороженное " аналитическое распределение # по умолчанию соответствует стандартному нормальному распределению, n~(0, 1) dist = stats .norm () # нарисуйте случайные выборки из населения, которое вы построили выше. # Это просто образец, так что среднее и ЗППП. отклонение должно быть близко к (1, 0). samp = dist.rvs (size = 1000 ) # `ppf ()`: функция процентных точек (инверсия cdf — процентилей). x = np.linspace (start = статистика .норм .ppf (0.01), stop = статистика .норм .ppf (0.99), num = 250) gkde = статистика .gaussian_kde (dataset = samp ) # `gkde.evaluate`) ' оценивает сам PDF. рис, ax = plt .subplots() ax.участок (x, dist .pdf (x), linestyle ='solid', c = 'red', lw = 3 , alpha = 0.8, label = 'Analytical (True) PDF') ax .участок (x, gkde .evaluate (x ), linestyle = 'dashed' , c = 'black' , LW = 2 , label = 'PDF оценивается через KDE' ) ax .легенда (loc = 'best' , frameon = False ) ax .set_title ('аналитический против оценки PDF') ax .set_ylabel ('вероятность') ax .текст ( - 2., 0.35, r ' $f (x) = frac{exp (- x^2/2)}{sqrt{2*pi}}$', fontsize = 12) Это больший кусок кода, так что давайте возьмем секунду, чтобы коснуться нескольких ключевых строк:
statsПодпакет SciPy позволяет создавать объекты Python, которые представляют собой аналитические распределения, из которых можно сделать выборку для создания фактических данных. Такимdist = stats.norm()образом, представляет собой нормальную непрерывную случайную величину, и вы генерируете из нее случайные числаdist.rvs().- Чтобы оценить как аналитический PDF, так и гауссовский KDE, вам нужен массив
xквантилей (стандартные отклонения выше/ниже среднего для нормального распределения).stats.gaussian_kde()представляет оценочный PDF-файл, который необходимо оценить в массиве, чтобы создать что-то визуально значимое в этом случае. - Последняя строка содержит латекс, который хорошо интегрируется с Matplotlib.
Причудливая альтернатива с Seaborn
Давайте внесем еще один пакет Python в микс. Seaborn имеет displot()функцию, которая строит гистограмму и KDE для одномерного распределения за один шаг. Использование массива NumPy dиз ealier:
импортируйте seaborn как sns sns .set_style ('darkgrid') sns .distplot(d) Вызов выше производит KDE. Существует также возможность подгонки под конкретное распределение данных. Это отличается от KDE и состоит из оценки параметров для универсальных данных и указанного имени распространения:
СНС .distplot (d , fit = статистика .laplace, KDE = False)
Опять же, обратите внимание на небольшое различие. В первом случае вы оцениваете какой-то неизвестный PDF; во втором вы берете известное распределение и находите, какие параметры лучше всего описывают его, учитывая эмпирические данные.
Другие инструменты в Pandas
В дополнение к инструментам построения графиков, Pandas также предлагает удобный .value_counts()метод, который вычисляет гистограмму ненулевых значений для Pandas Series:
>>>>>> >>> импорт панд как pd >>>>>> >>> data = np .Рэндом .выбор ( np .arange (10), size = 10000, ... p=np.linspace(1, 11, 10) / 60) >>> s = pd.Серия (данные ) >>>>>> >>> с.value_counts () 9 1831 8 1624 7 1423 6 1323 5 1089 4 888 3 770 2 535 1 347 0 170 dtype: int64 >>>>>> >>> С.value_counts (normalize = True).головка () 9 0.1831 8 0.1624 7 0.1423 6 0.1323 5 0.1089 dtype: float64
В другом месте, pandas.cut()это удобный способ бин значения в произвольные интервалы. Допустим, у вас есть некоторые данные о возрасте людей и вы хотите, чтобы ведро их разумно:
>>> ages = pd.Series( ... [1, 1, 3, 5, 8, 10, 12, 15, 18, 18, 19, 20, 25, 30, 40, 51, 52]) >>> bins = (0, 10, 13, 18, 21, np.inf) # The edges >>> labels = ('child', 'preteen', 'teen', 'military_age', 'adult') >>> groups = pd.cut(ages, bins=bins, labels=labels) >>> groups.value_counts() child 6 adult 5 teen 3 military_age 2 preteen 1 dtype: int64 >>> pd.concat((ages, groups), axis=1).rename(columns={0: 'age', 1: 'group'}) age group 0 1 child 1 1 child 2 3 child 3 5 child 4 8 child 5 10 child 6 12 preteen 7 15 teen 8 18 teen 9 18 teen 10 19 military_age 11 20 military_age 12 25 adult 13 30 adult 14 40 adult 15 51 adult 16 52 adult Приятно то, что обе эти операции в конечном итоге используют код Cython, который делает их конкурентоспособными по скорости, сохраняя при этом их гибкость.
Хорошо, Так Что Я Должен Использовать?
На данный момент Вы видели больше, чем несколько функций и методов на выбор для построения гистограммы Python. Как они сравниваются? Короче говоря, нет “одного размера для всех"."Вот краткое описание функций и методов, которые вы рассмотрели до сих пор, все из которых относятся к разбивке и представлению дистрибутивов в Python:
| У Вас Есть / Хотите | Рассмотрите Возможность Использования | Примечание(s) |
|---|---|---|
| Чистые целочисленные данные, размещенные в структуре данных, такой как список, кортеж или набор, и вы хотите создать гистограмму Python без импорта сторонних библиотек. | collections.Counter() из стандартной библиотеки Python предлагает быстрый и простой способ получить количество частот из контейнера данных. | Это частотная таблица, поэтому она не использует концепцию биннинга как “истинную” гистограмму. |
| Большой массив данных, и вы хотите вычислить” математическую " гистограмму, которая представляет бункеры и соответствующие частоты. | Numpy's np.histogram()и np.bincount()полезны для вычислять значения гистограммы численно и соответствуя края ящика. | Более того, проверьте np.digitize(). |
Табличные данные в панд Seriesили DataFrameобъекта. | Панды методы, такие какSeries.plot.hist(),DataFrame.plot.hist(),Series.value_counts(), иcut(), а также Series.plot.kde()и DataFrame.plot.kde(). | Ознакомьтесь с документами визуализации панды для вдохновения. |
| Создайте настраиваемый, точно настроенный график из любой структуры данных. | pyplot.hist() является широко используемой функцией построения гистограммы, которая использует np.histogram()и является основой для функций построения панд. | Matplotlib , и особенно его объектно-ориентированная структура, отлично подходит для тонкой настройки деталей гистограммы. Этот интерфейс может занять немного времени, чтобы освоить, но в конечном счете позволяет быть очень точным в том, как любая визуализация выложена. |
| Пре-законсервированные дизайн и интеграция. | Seaborn'sdistplot(), для комбинирования гистограммы и графика KDE или построения распределения. | По сути, "обертка вокруг обертки", которая использует гистограмму Matplotlib внутри, что, в свою очередь, использует NumPy. |
Бесплатный бонус: мало времени? Нажмите здесь, чтобы получить доступ к бесплатному двухстраничному чит-листу Python histograms, который суммирует методы, описанные в этом руководстве.
Вы также можете найти фрагменты кода из этой статьи вместе в одном скрипте на странице Real Python materials.
С этим, удачи создания гистограмм в дикой природе. Надеюсь, один из вышеперечисленных инструментов удовлетворит ваши потребности. Что бы вы ни делали, просто не используйте круговую диаграмму .
Источник: realpython.com