Персистетные гомологии и анализ текстовой информации

В сегодняшнем посте по мотивам статьи «Persistent homology: An introduction and a new text representation for natural language processing» мы будем анализировать (гомологически!) общее течение сюжета в художественных текстах. Повторы и отсылки к предыдущим событиям будут представляться элементами первых гомологий построенного по тексту комплекса Виеториса-Рипса с дополнительной структурой, отражающей основную последовательность событий текста.

В целом, выявление глобальных структур в текстовых документах звучит как что-то, где может помочь топологический анализ данных, распознающий паттерны в данных. Чтобы использовать методы TDA, сначала необходимо представить исходный текст как такие данные, а именно, как конечное подмножество в R^n. Один из простейших способов сделать это следующий. Разобьем текст на содержательные единицы x_1, … , x_m, — это могут быть абзацы, строчки или предложения, — каждая такая единица будет точкой в R^n. В качестве n возьмем количество различных слов, встречающихся во всем документе, тогда каждый элемент x_k представляется вектором (a_1, …, a_n), где a_i — количество повторений i-ого слова в x_k. Такое представление текстовой информации называется моделью «мешок слов».

Несомненным преимуществом такой модели является ее простота, однако вся грамматика и даже порядок слов внутри x_i никак не отражаются в данном представлении. Другой недостаток может возникнуть при обработке предлогов и артиклей — в текстовых документах они могут встречаться непропорционально чаще других слов. Методы «взвешенного» перечисления слов, такие как tf-idf позволяют справиться с этим недостатком. Также чаще всего перед переводом документа в облако данных, нужно провести его токенизацию : перевести все символы в нижний регистр, убрать знаки препинания и т.д. В русском языке, к примеру, может потребоваться обработка падежей.

Теперь, имея облако данных X, мы строим фильтрованный комплекс Виеториса-Рипса VR(X). В качестве напоминания: VR(X) состоит из последовательности вложенных симплициальных комплексов VR(X,r) для каждого положительного r. 0-симплексами служат точки X и комплекс VR(X,r) содержит симплекс с вершинами v_1,...,v_m, если попарные расстояния между вершинами не больше r. Если мы интересуемся вопросом схожести различных участков текстового документа, то функцию расстояния важно подобрать так, чтобы расстояние межу похожими участками текста было меньше, чем расстояние между непохожими. Обычное расстояние в R^n подойдет, также в обработке текстов часто используется угловое расстояние :

В полученном фильтрованном комплексе VR(X) не отражен тот факт, что точки X (элементы текста) имеют определенный порядок в документе. Простейший способ учесть порядок— это добавить 1-симплексы между точками x_i и x_{i+1} во все комплексы VR(X,r). Такое добавление, во-первых, сделает все VR(X,r) связными, а во-вторых, позволит детектировать отсылки между удаленными местами в документе, как петли в VR(X,r). Посмотрим на пример комплекса из четырех точек в R^2:

Можно представить, что эти точки получены из четырех параграфов некоего документа, в котором x_1 — это введение, x_2, x_3 — основная часть, а x_4 — заключение. Соответствующий комплекс VR(X,0.5) содержит 1-симплекс [x_1,x_4], его наличие отражает тот факт, что введение и заключение схожи в смысле модели мешка слов. Однако на уровне первых гомологий этот симплекс не считывается. Если теперь мы добавим 1-скелет, соответствующий порядку следования точек в документе, то этот же симплекс замкнет с ним петлю, давая нетривиальный вклад в первые гомологии:

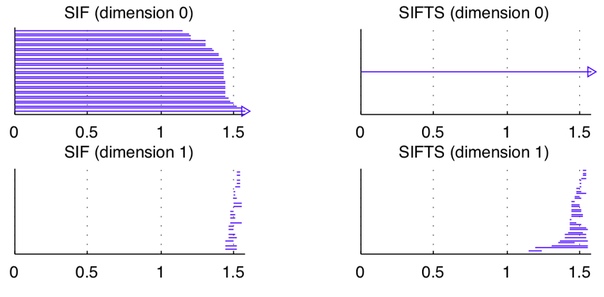
Соответствующие штрих-коды для H_0 и H_1 выглядят следующим образом:

Схожесть содержания введения и заключения, таким образом, становится видна на уровне H_1 (нижняя правая диаграмма). Без введения дополнительных 1-симплексов в этом примере ту же схожесть можно считать через слияние компонент связности, соответствующих x_1 и x_4 на верхней левой штрих-код диаграмме.

Перейдем к приложениям. В статье автор рассматривает детские стишки, читает «Алису» и «Красную Шапочку», сравнивает сочинения, написанные детьми и подростками.

Английская песенка Itsy Bitsy Spider:

The itsy bitsy spider went up the water spout.

Down came the rain, and washed the spider out.

Out came the sun, and dried up all the rain

And the itsy bitsy spider went up the spout again.

имеет ту же штрих-код диаграмму (в качестве точек взяты строчки песенки), что и комплекс, изображенный выше, последняя строчка замыкает повествование через отсылку к первой. А в «Красной Шапочке» (с разбиением на параграфы и угловым расстоянием между ними) первый возникающий 1-цикл образован фразами «Чтобы лучше тебя видеть, дорогая» и «Чтобы тебя съесть!», в английском оригинале, конечно:

Сравнивая сочинения детей и подростков, автор изучает, насколько сложнее со структурной точки зрения становятся тексты детей в процессе взросления, в частности, насколько увеличивается количество взаимосвязей между различными частями текста. Результаты приведены в следующей таблице:

В третьем столбце приведены результаты анализа тех же сочинений подростков, но обрезанных до одиннадцати предложений, — это сделано для того, чтобы длина сравниваемых сочинений детей и подростков была примерно одинакова (в среднем сочинения подростков вдвое длиннее).

Саму статью прикрепляю к посту, в ней упомянуты конкретные токенизации, используемые в каждому из примеров выше, а так же дано краткое введение в персистентные гомологии в целом.

Источник: m.vk.com

Комментарии: