Математика на страже либертарианства: теория игр, агентские модели и конкуренция по Тьебу

Чуть меньше двух лет назад один малоизвестный паблик с мемами решил привнести в российский либертарианский дискурс идею контрактных юрисдикций. И тогда эта идея прозвучала неоднозначно.

Во-первых, система юрисдикций утверждала, что с её появлением отпадет необходимость в таких базовых вещах для либертарианской этики, как принцип неагрессии (NAP) и естественные права. Эта идея звучала дико для тех, кто пришёл в анкап через Ротбарда и юснатурализм. Но её проще восприняли те люди, которые успели дорасти хотя бы до Дэвида Фридмана и его утилитаризма.

Во-вторых, обоснование юрисдикций зачастую сводилось к математическим выкладкам. Это не только увеличивало порог вхождения в тему, но и отсеивало многих ортодоксов, которые вслед за старыми австрийцами крайне скептически относились к математике в общественных науках. И относились совершенно напрасно.

О том, что современная экономическая математика в корне отличается от той, что была во времена Ротбарда и Мизеса мы уже писали. Пришло время поговорить о том, как должно выглядеть современное обоснование либертарианства через эту математику. О том, как можно запустить на своем компьютере 300-строчный код на Питоне и увидеть работоспособность юрисдикций своими глазами. Больше не требуется верить идеям либертарианства на слово, потому что вы можете проверить их сами.

ЧАРЛЬЗ ТЬЕБУ И ЕГО ОБЩЕСТВЕННЫЕ БАССЕЙНЫ

Как это обычно бывает, самое убедительное обоснование анкапа подъехало от человека, который анкапом никогда не являлся. Который умер до того, как либертарианство стало "вируситься" в Америке и расходиться по всему миру. Этим человеком был американский экономист-географ Чарльз Тьебу (1924-1968). И однажды его заинтересовала проблема безбилетника на уровне локальных общественных благ. Что это такое?

Представьте себе муниципалитет, который решил проспонсировать постройку общественного бассейна. По умолчанию принято считать, что бассейн в этой модели считается неделимым благом, его потребление неконкурентно и неисключаемо.

Неделимость означает, что посещение бассейна — это услуга. Она не может быть расфасована по пакетам и продана индивидуально, как товар.

Неконкурентность означает, что если бассейном пользуется n человек, то своим появлением n+1 посетитель не создаст помех всем остальным.

Неисключаемость означает, что вы не сможете отстранять от посещения бассейна каких-то отдельных лиц. Или сможете, но с очень высокими издержками.

У потенциальных посетителей бассейна есть две конкурирующие мотивации. Во-первых, хотелось бы, чтобы на этот общественный бассейн скинулось как можно больше народу. Всё-таки в одиночку содержать целый бассейн это накладно. Во-вторых, путешествовать на другой конец страны в свой бассейн – не самое разумное использование ресурсов. Поэтому, предположил Тьебу, в этой ситуации возникнет спонтанное разбиение всего общества на множество центров местной власти. Эти райцентры будут предоставлять своим резидентам локальные общественные блага. Условно говоря, десять тысяч человек скидываются на содержание публичной библиотеки и строят её в райцентре. Рабочий компромисс между двумя мотивами агентов найден.

На первый взгляд все выглядит незамысловато, даже тривиально. Когда Тьебу описал этот концепт в своей статье 1956 года «Чистая теория местных бюджетов» (A pure theory of local expenditures), он не предоставил никаких серьёзных математических выкладок. В конце концов, он был географом, а не математиком. Но зато он выстроил очень плодотворный toolbox и породил абсолютно новый способ думать о разделении властей и о логике местного самоуправления. Именно поэтому статья Тьебу накопила более 18 тысяч цитирований и во многом стала предтечей Вирджинской школы общественного выбора (Public choice), доказав возможность говорить о политике на экономическом языке.

До сих пор с переменным успехом и то затухающей, то расходящейся вновь интенсивностью, на страницах экономических журналов JPE и Public Choice, идет дискуссия между идейными последователями Тьебу и теми, кого его аргумент не убедил. Первые считают, что такое разделение общества на локальные юрисдикции решает проблему безбилетника и приводит ситуацию к эффективному равновесию. Вторые называют себя "неоконсолидационистами" и считают модель Тьебу недоработанной и неуниверсальной. Применимой только в условиях крупных мегаполисов.

А дальше началась математизация работ Тьебу, которую проводили неоклассики, институционалисты и выходцы из Вирджинской школы общественного выбора.

КАК МАТЕМАТИКА ПРИШЛА НА ВЫРУЧКУ К ЛИБЕРТАРИАНСТВУ

Математики — это потрясающие люди. Их метод решения проблем буквально вывернут наизнанку. Если обычный человек сначала сталкивается с проблемой, а затем ищет пути её решения, то математик поступает в обратной последовательности. Сначала изобретает пути выхода из какой-то проблемы. И только потом идет на поиски какой-то проблемной отрасли знания, где его модели и выкладки помогут выйти из логического тупика.

Поскольку изобретать модели приходится в пространстве голой математики, а находить им применение уже в чем-то более прикладном, то все математики невольно являются междисциплинарными исследователями. Поэтому неудивительно, что идее контрактных юрисдикций в их современном понимании насчитывается меньше 10 лет, а моделям, свидетельствующим в пользу КЮ исполняется уже по 30-40 лет.

Серьёзные математические выкладки в модели Тьебу появились не раньше 1980-х, когда проблемой глубоко заинтересовались исследователи Теории игр. Они выяснили, что несмотря на крайне простую формулировку, закрытая форма решения для состояний в модели Тьебу почти никогда не бывает достижима. Другими словами, Тьебу удалось простым описательным языком поднять и сформировать огромный пласт проблем, который математики ещё не успели систематизировать. В дальнейшем на модели Тьебу были отработаны многие инновационные теоретико-игровые техники вроде сильного равновесия Нэша и коалиционной устойчивости.

Сильное равновесие Нэша. Значит бывает ещё и слабое? По умолчанию принято считать, что слабое равновесие Нэша и обычное равновесие Нэша это равнозначные термины. Проще всего рассмотреть эту концепцию на примере уже приевшейся всем дилеммы заключенного.

Обычное равновесие Нэша в доминирующих стратегиях выглядит так: оба игрока всегда доносят друг на друга. Почему? Ну хотя бы потому, что ни у одного из игроков нет стимула отклониться от равновесного поведения В ОДНОСТОРОННЕМ ПОРЯДКЕ.

Сильное равновесие Нэша предъявляет к равновесиям гораздо более строгие требования: в равновесии не только ни один агент не должен хотеть отклоняться от выбранной стратегии, но НИ ОДНО ПОДМНОЖЕСТВО агентов не должно иметь такого соблазна. Эта конструкция позволяет учесть в модели возможность сговора: действительно, если подозреваемые содержатся в смежных камерах и имеют возможность переговариваться через стенку, вероятность «кооперации» значительно возрастает. Иными словами, сильное равновесие Нэша – это мостик, натянутый над бездной между некооперативными и кооперативными играми.

Требование, чтобы в игре было сильное равновесие Нэша в последнее время стало хорошим тоном в дизайне механизмов. Так агенты с гораздо меньшей вероятностью будут отклоняться от эффективного равновесия, заложенного механизм-дизайнером.

В модели Тьебу до сих пор неочевидно, какие действия агентам необходимо разрешить, а какие можно запретить, не умаляя общности. Понятно, что система в некоторой степени должна быть коалиционно устойчивой, то есть равновесие должно предполагать не только отсутствие стимулов отклониться от равновесной стратегии (здесь – юрисдикции, к которой агент присоединяется), но и некоторую защиту от широкого класса коалиционных отклонений (coalition proof). Под этими отклонениями понимают ситуацию, при которой несколько агентов встречаются и пытаются сформировать свою собственную юрисдикцию, в которой каждый из агентов улучшит свое положение по сравнению со статус-кво. Но в то же самое время очевидно, что требовать абсолютной коалиционной устойчивости от равновесия глупо, так как в системе не все агенты лично знают друг друга, чтобы успешно планировать подобные отклонения.

В начале нулевых годов произошло сразу несколько качественных прорывов. Сначала появилась концепция «миграционной устойчивости» (migration proof), которая предотвращает не все отклонения, а только те, которые являются устойчивыми сами по себе. Метким языком авторов статьи, «уезжать в другой город от надоедливой тещи бессмысленно, если вы знаете, что она может тут же последовать за вами». Было показано, что равновесия с миграционной устойчивостью во-первых, более реалистичны, а во-вторых, Парето-эффективны, что было ощутимым прорывом для модели.

Также в нулевых годах в этой дискуссии был замечен экономист Брайан Каплан, известный как анкап-неоклассик, самый последовательный сторонник политики открытых границ и автор двух отличных книжек «Мифа о рациональном избирателе» и «The case against education». Каплан доказал, что конкуренция по Тьебу возможна только тогда, когда юрисдикции не могут заниматься налогообложением имущества. Потому что в противном случае налог тут же капитализируется в цене, и голосование ногами становится неэффективно. В итоге мы наблюдаем не конкуренцию юрисдикций и не расцвет анкапа, а откат к государствам и бюрократизацию муниципальных органов. Иными словами, даже на переходном периоде к контрактным юрисдикциям не должно существовать никакого налога на имущество ни в какой его форме.

ОБОСНОВЫВАЕМ ЛИБЕРТАРИАНСТВО С ПОМОЩЬЮ ПИТОНА

На протяжении десятилетий, пока модель Тьебу оставалась на ближайшей периферии академического дискурса в public choice, её применяли для двух случаев.

Первый — сугубо пространственный экономический анализ. Двухмерный случай, где «центры», к которым присоединяются агенты – это локальные общественные блага (бассейны или публичные библиотеки), финансируемые из местных бюджетов.

Второй —анализ формирования партий в идеологическом пространстве политических взглядов. Метод главных компонент показал, что в большинстве стран и культур этих измерений два, поэтому в следующий раз, когда будете делать мемы о политических координатах, знайте, что этот ваш выбор научно обоснован.

В какой-то момент времени дискурсу понадобился сумасшедший либертарианец, который взглянул на модель Тьебу и сказал – «А что если соединить пространственные и идеологические размерности и сделать наши центры предоставления локальных общественных благ центрами предоставления ВСЕХ общественных благ, включая законотворчество и обеспечение правопорядка? Тогда у нас получится система, очень похожая на то, что мы называем контрактными юрисдикциями.»

Предположим, что у есть четыре измерения (два географических и два идеологических), нормирующихся к единичному отрезку. И есть две контрактные юрисдикции, обе базирующиеся в географических координатах (0,5; 0,5), только первая имеет координаты (0;0), а вторая – (1;1). Грубо говоря, первая – это авторитарный левый гулаг, а вторая – капиталистический рай, но конторы зарегистрированы через дорогу. И жители окрестностей смогут подписываться как к первой, так и ко второй, в зависимости от своих предпочтений и движимые мотивом минимизации общих издержек. Транспортные издержки, таким образом, переопределяются как преференциальные и суммируются из географических и идеологических издержек. Это выражается в желании потребителей ходить в общественный бассейн поближе к дому, но при этом потребитель готов пройти пару кварталов, только чтобы не плавать в одной луже с коммунистами.

В чем же смысл системы контрактных юрисдикций с точки зрения модели Тьебу? В чем ее потенциал с точки зрения увеличения потребительской полезности по сравнению с альтернативами? Все очень просто: в текущих реалиях, система «территориальных юрисдикций» присоединяет агентов к себе, по дефолту учитывая лишь два измерения – пространственные. Экстерриториальные контрактные юрисдикции позволят принимать во внимание не только «географические», но и «идеологические» преференцинальные издержки, приводя к более эффективному равновесию, с точки зрения минимизации издержек её агентов.

Для иллюстрации модели и для свидетельства тому, что авторы – не простые пустозвоны, я написал несколько программ на Питоне, которые по сути являются агентскими моделями контрактных юрисдикций в духе Тьебу. Для более чёткой формализации код написан для ряда систем изначальных допущений, и файлы в формате .ipynb выложены в открытый доступ с подробнейшими комментариями, чтобы каждый мог в своем Джупитере поиграться с переменными и полюбоваться своими собственными графиками территориального разбиения агентов на контрактные юрисдикции. Всего создано несколько моделей:

1) Детерминистичная модель. Локации контрактных юрисдикций в n-мерном пространстве считаются определенными заранее, и агенты никак не могут повлиять на их расположение. Им разрешается отсоединяться от текущих юрисдикций в одностороннем порядке и присоединяться к любым другим, если это будет выгоднее.

2) Модель медианного избирателя. То же самое, что 1), но агенты могут проголосовать о том, где в n-мерном пространстве будет располагаться центр их юрисдикции. Поэтому его расположение по каждой координате будет медианой координат резидентов. Это относительно простое и реалистичное моделирование процесса голосования.

3) Модель мизесианской сецессии. Мизес в «Либерализме» озвучил интересное предложение, по сути являющееся доведением права наций на самоопределение до логического конца. Он сформулировал принцип индивидуалистической сецессии, когда каждый индивид может в одностороннем порядке выйти из «общественного договора». Эта концепция «мизесианской сецессии» легко реализуема в этой модели: агенты просто могут проверить, выгоднее ли им быть резидентами каждой из существующих юрисдикций либо не быть резидентами ни одной из них, самостоятельно обеспечивая необходимый уровень общественных благ для себя в одиночку.

4) Модель мизесианской сецессии с медианным избирателем. Совмещение 2) и 3). Агенты вольны как выходить из юрисдикций в одностороннем порядке, так и определять локацию своих юрисдикций с помощью голосования.

5) Модель коалиционной устойчивости. То же, что и 4), однако с добавлением возможности коалиционного отклонения от равновесия. Каждую итерацию агенты случайным образом отбираются в группу «потенциальных девиантов» и проверяют, будет ли им выгоднее, если они сформируют свою собственную контрактную юрисдикцию. Если да, то они откалываются от текущих юрисдикций и создают свою. Если нет, то они расходятся по своим делам и действуют согласно вышеупомянутым алгоритмам. Нетривиальным является вопрос, как именно отбирать агентов для наиболее реалистичного учета процесса коалиционных отклонений. Я рассматриваю две возможности:

а) Выбор по Кальво, когда у каждого агента есть фиксированная и экзогенно заданная вероятность быть отобранным в эту потенциальную коалицию в каждой итерации.

б) Когда эта вероятность положительно зависит от текущего уровня общих издержек, которые агент несет в своей текущей юрисдикции (то есть, самые «неудовлетворенные» агенты имеют большую вероятность задумываться о коалиционном отклонении.

ВЫВОДЫ АГЕНТСКОЙ МОДЕЛИ

1) По сравнению со случайным изначальным разделением на юрисдикции, и даже по сравнению с разделением на юрисдикции согласно изначальному территориальному местоположению (когда агенты автоматически присоединяются к той юрисдикции, к которой они ближе всего географически, сильно напоминает текущее положение вещей, не правда ли?), ЛЮБАЯ модель, разрешающая добровольные отклонения, приводит к значительной, просто монументальной, экономии издержек. Обратим ваше внимание на то, что агенты здесь учитывают сугубо свои личные интересы, а в итоге ощутимо снижаются издержки общественные. Говоря языком мемов, рыночек решает. Оказывается, невидимая рука может действовать не только на привычных нам рынках, но и на таком вот оригинальном квазирынке общественных благ.

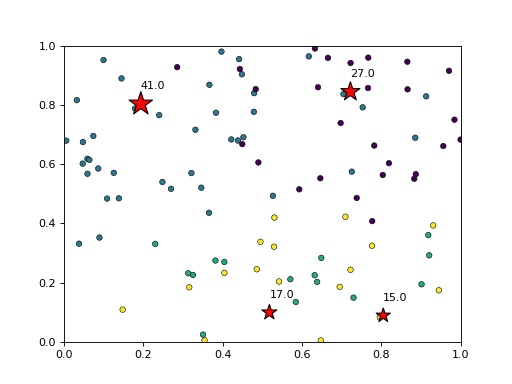
2) Демократия, то есть возможность агентов влиять на местоположение, как географическое, так и идеологическое, юрисдикции, резидентами которой они являются, сильно переоценена. Экономия на издержках в демократических сценариях лишь незначительно выше, чем в недемократических сценариях. Вот вам и математическое подтверждение того, что самое эффективное голосование – это голосование ногами, а голосование политическое – в лучшем случае лишь приятное к нему дополнение.

3) Мизесианская сецессия (то есть возврат агентов в естественное состояние, то, что можно назвать базовым сценарием анкапа без надстроек) очень эффективна, когда издержки финансирования общественных благ относительно низки. Действительно, если каждый индивид может защитить себя сам, перспективы какой-то эффективной кооперации на этом фронте весьма сомнительны, и в этом сценарии лучше никому друг друга просто не трогать. В то же самое время, когда издержки относительно высоки, модели мизесианской сецессии как с демократией, так и без неё, показывают себя куда хуже аналогов.

4) Даже на горизонте тысяч итераций система контрактных юрисдикций коалиционно устойчива. Если изначальное положение из рук вон плохо, то в первые несколько итераций агенты закопошатся и сформируют одну-две юрисдикции. Впоследствии, так как юрисдикции становятся открытыми для добровольного присоединения к ним других агентов, система очень быстро сходится к равновесию, из которого ее потом почти невозможно вывести. Агентские модели показывают, что беспокойства о коалиционной неустойчивости контрактных юрисдикций сильно преувеличены.

И что мы имеем в сухом остатке? Рынки гораздо более многообразны и куда более адаптивны, чем вы можете себе представить. Если обратиться к монументальному пласту матэкономической литературы, сформировавшейся в последние несколько десятилетий, можно найти множество эффективных инструментов для моделирования практически любой системы общественного устройства, а если вы умеете немножко кодить на Питоне, то вы сможете собственноручно посмотреть, как ваши доморощенные агенты будут прыгать из юрисдикции в юрисдикцию. Сегодня, когда экономическая наука движется вперед семимильными шагами, будущее человеческой самоорганизации кажется как никогда многообещающим.

Голосуйте ногами во всех случаях, когда вам это доступно и выгодно. Как видите, в пользу эффективности этого вида голосования куда больше свидетельств.

Ссылки на исследования:

1) Tiebout, C. (1956). A pure theory of local expenditures. Journal of political economy, 64(5), 416-424.
https://www.journals.uchicago.edu/doi/pdfplus/10.1086..2) Caplan, B. (2001). Standing Tiebout on his head: Tax capitalization and the monopoly power of local governments. Public Choice, 108(1-2), 101-122.https://pdfs.semanticscholar.org/af53/e8e3a47d75d20ec..3) Boettke, P., Coyne, C., & Leeson, P. (2011). Quasimarket failure. Public Choice, 149(1-2), 209.https://mpra.ub.uni-muenchen.de/33068/1/MPRA_paper_33..4) Conley, J., & Konishi, H. (2002). Migration-proof Tiebout equilibrium: existence and asymptotic efficiency. Journal of Public Economics, 86(2), 243-262.http://citeseerx.ist.psu.edu/viewdoc/download?doi=10...5) Greenberg, J., & Weber, S. (1986). Strong Tiebout equilibrium under restricted preferences domain. Journal of Economic Theory, 38(1), 101-117.https://www.sciencedirect.com/science/article/pii/002..6) Savvateev, A., Sorokin, C., & Weber, S. (2018). Multidimensional free-mobility equilibrium: Tiebout revisited. arXiv preprint arXiv:1805.11871.https://arxiv.org/pdf/1805.11871

Источник: m.vk.com

Комментарии: