«Perceptron Learning Algorithm» — прикладные задачи ML & Data Science

В прошлой статье я рассказывал Вам о том, что такое градиентный спуск, приводил как математическое обоснование этой модели так и ее реализацию путем написания кода на ЯП Python 3.0. Но на этом модели и прикладные математические методы которые активно используются в машинном обучение не заканчиваются. Сразу стоит понимать то, что самые первые методы и модели начали появляться еще в 50 — 60 годах прошлого века, на сегодняшний день их слишком много, чтобы перечислить все, а так же разрабатываются все новые. На этот раз в нашем рассмотрение будет одна из самых первых моделей, теоретические обоснования которой смогли описать еще в 60 годах — «Перцептрон».

Как всегда, сначала небольшой introduction и описание того, что же это за модель. Перцептрон — это модель (компьютерная или математическая) описания того, как наши нейроны в головном мозге человека, воспринимают информацию, обрабатывают ее и делают дальнейшие операции с ней. Модель была предложена в 1957 году Фрэнком Розенблаттом (ученый в области психологии и искусственного интеллекта) а затем была произведена реализация на первый в мире нейрокомпьютер — «Mark I». Таким образом эта модель стала первой в мире искусственной нейронной сетью.

Далее рассмотрим принцип работы этой модели. Отсюда должно быть очевидно то, что модель первая в мире, а значит что то глобальное от нее не стоит ожидать, поэтому она имеет достаточно простой математический аппарат и саму архитектуру построения.

Итак, что мы имеем: входные точки обозначенные как x1, x2, x3 … xN, окружность посередине которая работает в качестве функции, которая обработает входные данные, ну и соответсвенно выход уже готовых данных. Все просто. Стоит понимать что выход является бинарным — либо 1, либо 0.

Розенблатт предложил в свое время простой принцип вычисления, а именно — добавления весовых коэффициентов — w1, w2, w3 … wN. Эти весовые коэффициенты имеют только одно предназначение — они определяют вещественные числа, которые выражают важность входов по отношению к выходу в модели. С первого раза может быть не совсем понятно и запутанно, но это лучше описать математической формулой для наглядности.

Эта одна простая формула определяют всю математическую модель перцептрона. Теперь подробно опишем ее: имеется выход модели и он определяется следующими показателям — логический 0 или 1. Бинарные показатели на выходе определяются по двум условиям: на выходе будет 0 если сумма весовых коэффициентов и сумма входов будет меньше либо равна порогу. И следующее условие: на выходе будет 1 если сумма весовых коэффициентов и сумма входов будет больше чем порог. Как видим, все достаточно просто. В нашем случае значение порога может являться какой либо константой, либо динамическим значением, которое мы сами, отталкиваясь от задачи, можем изменить.

По началу может показаться, что это аналогия алгоритма принятия решений и решающих деревьев, но стоит углубиться и Вы поймете что различия все таки имеются.

В решающих деревьях мы ставим условие по которому двигаемся по дереву дальше, попадая на другие условия, а затем приходя к результату. Какие различия у нас имеются тут? Приводим простую аналогию из реальной жизни:

— Вы узнаете о том, что в вашем городе будет проходить крутая конференция по программированию, на которую вы были бы не против сходить. Какими же факторами будет определяться то, что пойдете ли вы туда?

1. Какая погода на улице? — Хорошая или плохая
2. В удобное ли для вас время будет мероприятие?
3. Пойдете ли вы одни туда или с вами согласятся пойти ваши друзья?

Эти три фактора предостаточно, чтобы полностью описать поведение модели и определить, пойдете ли Вы все таки на конференцию или нет.

Следующее что мы делаем, переводим все наши факторы в бинарный вид:

x1 = Хорошая погода — 1, плохая — 0.

x2 = Удобное время — 1, не удобное — 0.

x3 = Пойдете с друзьями — 1, без друзей — 0.

Модель выглядит слишком простой без наших весовых коэффициентов. Пришло время их задействовать :)

Представьте что очень ждете эту конференцию или программируете на том языке, который там активно будет обсуждаться, вы готовы пойти туда даже если на улице будет плохая погода, или друзья не смогут составить Вам компанию. Но помните то, что вы не будете рисковать ради этого мероприятия своим временем. Отсюда можно сделать следующее: установим значение w1 = 7 для времени (удобно или не удобно), w2 = 3 и w3 = 2 для остальных факторов.

Далее путем нехитрых математических действий понятно то, что w1 > w2 и w3. Это значит только одно — ваше время для Вас является очень ценным и вы не пойдете на конференцию даже тогда, когда будет хорошая погода и друзья смогут составить вам компанию, но Вам не позволяет время — весовой коэффициент w1.

Мы описали простую модель перцептрона, которая полностью не охватывает те решения, которые использует человек повседневно. Но стоит понимать то, что такие одиночные модели можно объединять во множество перцептронов, соответсвенно и модель будет сложнее и принятие решений она может анализировать лучше.

Как видим, входов может быть столько, сколько потребуется в задачи, но на выходе мы получаем все тот же единый перцептрон, который в конце так же произведет вычисления и даст данные на выходе. Немаловажный фактор того, что с помощью этой модели можно построить все базовые логические элементы: И, ИЛИ, И-НЕ и затем задействовать их в своей модели для принятия и анализа какого либо решения.

Реализуем модель перцептрона с помощью Python и библиотеки Sklearn:

Изначально импортируем метод load digits — позволяет нам загрузить цифровые данные и вернуть их (с помощью метода print (X, y) будут предоставлены в виде матрицы).

Затем из линейных моделей — импортируем Перцептрон (Да, стоит понимать и то, что однослойный перцептрон — это линейный алгоритм)

Далее обозначим что X и Y = наши загружаемые данные, которые возвращаются с помощью логического значения True.

Затем определяем что clf (классификатор оценки) в модели перцептрона, в нее мы передаем tol (критерий остановки) который равен 1 * 10^-3 = 0.003, а так же значение random_state = 0 (генерацию случайных числовых значений).

Далее к нашему классификатору оценки применим метод .fit — этот метод позволит нашему классификатору обучиться (за счет прогона через нашу выборку)

Далее рассмотрим саму модель перцептрона, которая в нашем случае является массивом: alpha — константа для умножения значения регуляризации (по дефолту = 0.0001)

Регуляризация в статистике, машинном обучении, теории обратных задач — метод добавления некоторых дополнительных ограничений к условию с целью решить некорректно поставленную задачу или предотвратить переобучение. Эта информация часто имеет вид штрафа за сложность модели.

Class_weight = None — к весу присваиваем тип None — нейтральное значение.

Early_stopping = None — раняя остановка, которая сделает прерывания обучения. Проверка пройдет по условию: выдаются данные, если не происходит улучшения — остановка, иначе — продолжить обучение.

Eta0 = 1.0 — константа, на которую умножается коэффициент alpha (по дефолту = 1)

Fit_intercept = True — метод который рассчитывает, производить ли перехват задействованной модели (если True) или данные уже являются центрированы (Другой пример — линейная регрессия)

Max_iter = None — максимальное колл-во итераций. N_iter = None — колл-во итераций по данным выборки для обучения модели. n_iter_no_change = 5 — колл-во итераций для ранней остановки, если не будет прогресса в обучении модели (по дефолту = 5) n_jobs = None — колл-во процессов используемых для OVA (One versus all — один против всех) — метод который применяется в так называемой мульти-классовойстратегии.

penalty=None — штраф (она же — регуляризация)

shuffle=True — перетасовка и перебор всей выборки после каждой эпохи.(Эпоха — когда вся наша выборка или датасет проходит через нейронную сеть прямо и обратно за один раз)

tol = 0.001 — Критерий остановки. Если это не None, итерации остановятся, когда (loss > previous_loss-tol). По умолчанию нет. По умолчанию 1 * 10 ^-3 от 0.21.

validation_fraction=0.1 = критерий валидационной выборки из наших данных, которая отвечает за то, на сколько модель обучается правильно. Задействует бинарные значения добавляя плавающую точку от 0.0 до 9.9 ? 1. Используется только тогда, когда значение Early_stopping = True.

verbose = 0 — уровень детализации, который будет задействован в процессе вывода в стандартный поток (как пример — изображения для распознавания объекта на нем)

warm_start = False — Если флаг = True, повторно будет использовано решение предыдущего вызова в качестве инициализации. Если стоит флаг False — прошлое решение удаляется .

Итог вызова нашего классификатора, с помощью метода score:

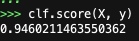
Как видим, наша модель классификации достаточно точно дала на выходе единицу, что уже довольно не плохо.

На этом все, надеюсь что вы остались со мной до конца. Стоит понимать самое главное — Machine Learning & Data Science на сегодняшний день является одной из самых сложных инженерных отраслей науки и индустрии, на стыке математики и компьютерных наук. Это не тот момент, когда можно с легкостью влиться в область — порог вхождения достаточно высок. Но на этом не стоит останавливаться. Желаю Вам удачи. Учиться, учиться и еще раз учиться :)

Источник: m.vk.com

Комментарии: