Логистическая функция ошибки

Эту функцию называют также «логлосс» (logloss / log_loss), перекрёстной / кросс-энтропией (Cross Entropy) и часто используют в задачах классификации. Разберёмся, почему её используют и какой смысл она имеет. Для чтения поста нужна неплохая ML-математическая подготовка, но даже новичкам я бы рекомендовал почитать (хотя я не очень заботился, чтобы «всё объяснялось на пальцах»).

Начнём издалека…

Вспомним, как решается задача линейной регрессии. Итак, мы хотим получить линейную функцию (т.е. веса w), которая приближает целевое значение с точностью до ошибки:

Здесь мы предположили, что ошибка нормально распределена, x – признаковое описание объекта (возможно, в нём есть и фиктивный константный признак, чтобы в линейной функции был свободный член). Тогда мы знаем как распределены ответы нашей функции и можем записать функцию правдоподобия выборки (т.е. произведение плотностей, в которые подставлены значения из обучающей выборки) и воспользоваться методом максимального правдоподобия (в котором для определения значений параметров берётся максимум правдоподобия, а чаще – его логарифма):

В итоге оказывается, что максимизация правдоподобия эквивалентна минимизации среднеквадратичной ошибки (MSE), т.е. эта функция ошибки не зря широко используется в задачах регрессии. Кроме того, что она вполне логична, легко дифференцируема по параметрам и легко минимизируется, она ещё и теоретически обосновывается с помощью метода максимального правдоподобия в случае, если линейная модель соответствует данным с точностью до нормального шума.

Давайте ещё посмотрим, как реализуется метод стохастического градиента (SGD) для минимизации MSE: надо взять производную функции ошибки для конкретного объекта и записать формулу коррекции весов в виде «шага в сторону антиградиента»:

Получили, что веса линейной модели при её обучении методом SGD корректируются с помощью добавки вектора признаков. Коэффициент, с которым добавляют, зависит от «агрессивности алгоритма» (параметр альфа, который называют темпом обучения) и разности «ответ алгоритма – правильный ответ». Кстати, если разница нулевая (т.е. на данном объекте алгоритм выдаёт точный ответ), то коррекция весов не производится.

Log Loss

Теперь давайте, наконец, поговорим о «логлоссе». Рассматриваем задачу классификации с двумя классами: 0 и 1. Обучающую выборку можно рассматривать, как реализацию обобщённой схемы Бернулли: для каждого объекта генерируется случайная величина, которая с вероятностью p (своей для каждого объекта) принимает значение 1 и с вероятностью (1–p) – 0. Предположим, что мы как раз и строим нашу модель так, чтобы она генерировала правильные вероятности, но тогда можно записать функцию правдоподобия:

После логарифмирования правдоподобия получили, что его максимизация эквивалентна минимизации последнего записанного выражения. Именно его и называют «логистической функции ошибки». Для задачи бинарной классификации, в которой алгоритм должен выдать вероятность принадлежности классу 1, она логична ровно настолько, насколько логична MSE в задаче линейной регрессии с нормальным шумом (поскольку обе функции ошибки выводятся из метода максимального правдоподобия).

Часто гораздо более понятна такая запись logloss-ошибки на одном объекте:

Отметим неприятное свойство логосса: если для объекта 1го класса мы предсказываем нулевую вероятность принадлежности к этому классу или, наоборот, для объекта 0го – единичную вероятность принадлежности к классу 1, то ошибка равна бесконечности! Таким образом, грубая ошибка на одном объекте сразу делает алгоритм бесполезным.На практике часто логлосс ограничивают каким-то большим числом (чтобы не связываться с бесконечностями).

Если задаться вопросом, какой константный алгоритм оптимален для выборки из q_1 представителей класса 1 и q_0 представителей класса 0, q_1+ q_0 = q , то получим

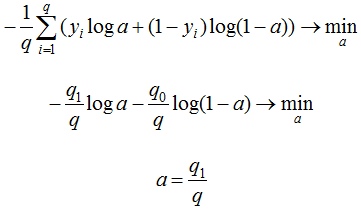
Последний ответ получается взятием производной и приравниванием её к нулю. Описанную задачу приходится решать, например, при построении решающих деревьев (какую метку приписывать листу, если в него попали представители разных классов). На рис. 2 изображён график log_loss-ошибки константного алгоритма для выборки из четырёх объектов класса 0 и 6 объектов класса 1.

Представим теперь, что мы знаем, что объект принадлежит к классу 1 вероятностью p, посмотрим, какой ответ оптимален на этом объекте с точки зрения log_loss: матожидание нашей ошибки

Для минимизации ошибки мы опять взяли производную и приравняли к нулю. Мы получили, что оптимально для каждого объекта выдавать его вероятность принадлежности к классу 1! Таким образом, для минимизации log_loss надо уметь вычислять (оценивать) вероятности принадлежности классам!

Если подставить полученное оптимальное решение в минимизируемый функционал, то получим энтропию:

Это объясняет, почему при построении решающих деревьев в задачах классификации (а также случайных лесов и деревьях в бустингах) применяют энтропийный критерий расщепления (ветвления). Дело в том, что оценка принадлежности к классу 1 часто производится с помощью среднего арифметического меток в листе. В любом случае, для конкретного дерева эта вероятность будет одинакова для всех объектов в листе, т.е. константой. Таким образом, энтропия в листе примерно равна логлосс-ошибке константного решения. Используя энтропийный критерий мы неявно оптимизируем логлосс!

В каких пределах может варьироваться logloss? Ясно, что минимальное значение 0, максимальное – +?, но эффективным максимальным можно считать ошибку при использовании константного алгоритма (вряд же мы в итоге решения задачи придумаем алгоритм хуже константы?!), т.е.

Интересно, что если брать логарифм по основанию 2, то на сбалансированной выборке это отрезок [0, 1].

Связь с логистической регрессией

Слово «логистическая» в названии ошибки намекает на связь с логистической регрессией – это как раз метод для решения задачи бинарной классификации, который получает вероятность принадлежности к классу 1. Но пока мы исходили из общих предположений, что наш алгоритм генерирует эту вероятность (алгоритмом может быть, например, случайный лес или бустинг над деревьями). Покажем, что тесная связь с логистической регрессией всё-таки есть… посмотрим, как настраивается логистическая регрессия (т.е. сигмоида от линейной комбинации) на эту функцию ошибки методом SGD.

Как видим, корректировка весов точно такая же, как и при настройке линейной регрессии! На самом деле, это говорит о родстве разных регрессий: линейной и логистической, а точнее, о родстве распределений: нормального и Бернулли. Желающие могут внимательно почитать лекцию Эндрю Ына.

Во многих книгах логистической функцией ошибки (т.е. именно «logistic loss») называется другое выражение, которое мы сейчас получим, подставив выражение для сигмоиды в logloss и сделав переобозначение: считаем, что метки классов теперь –1 и +1, тогда

Полезно посмотреть на график функции, центральной в этом представлении:

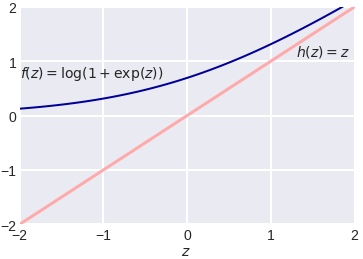
Как видно, это сглаженный (всюду дифференцируемый) аналог функции max(0, x), которую в глубоком обучении принято называть ReLu (Rectified Linear Unit). Если при настройке весов минимизировать logloss, то таким образом мы настраиваем классическую логистическую регрессию, если же использовать ReLu, чуть-чуть подправить аргумент и добавить регуляризацию, то получаем классическую настройку SVM:

выражение под знаком суммы принято называть Hinge loss. Как видим, часто с виду совсем разные методы можно получать «немного подправив» оптимизируемые функции на похожие. Между прочим, при обучении RVM(Relevance vector machine) используется тоже очень похожий функционал:

Связь с расхождением Кульбака-Лейблера

Расхождение (дивергенцию) Кульбака-Лейблера (KL, Kullback–Leibler divergence) часто используют (особенно в машинном обучении, байесовском подходе и теории информации) для вычисления непохожести двух распределений. Оно определяется по следующей формуле:

где P и Q – распределения (первое обычно «истинное», а второе – то, про которое нам интересно, насколько оно похоже на истинное), p и q – плотности этих распределений. Часто KL-расхождение называют расстоянием, хотя оно не является симметричным и не удовлетворяет неравенству треугольника. Для дискретных распределений формулу записывают так:

что в точности совпадает с logloss.

Настройка на logloss

Один из методов «подгонки» ответов алгоритма под logloss – калибровка Платта (Platt calibration). Идея очень простая. Пусть алгоритм порождает некоторые оценки принадлежности к 1му классу – a. Метод изначально разрабатывался для калибровки ответов алгоритма опорных векторов(SVM), этот алгоритм в простейшей реализации разделяет объекты гиперплоскостью и просто выдаёт номер класса 0 или 1, в зависимости от того, с какой стороны гиперплоскости объект расположен. Но если мы построили гиперплоскость, то для любого объекта можем вычислить расстояние до неё (со знаком минус, если объект лежит в полуплоскости нулевого класса). Именно эти расстояния со знаком r мы будем превращать в вероятности по следующей формуле:

неизвестные параметры ?, ? обычно определяются методом максимального правдоподобия на отложенной выборке (calibration set).

Проиллюстрируем применение метода на реальной задаче, которую автор решал недавно. На рис. показаны ответы (в виде вероятностей) двух алгоритмов: градиентного бустинга (lightgbm) и случайного леса (random forest).

Видно, что качество леса намного ниже и он довольно осторожен: занижает вероятности у объектов класса 1 и завышает у объектов класса 0. Упорядочим все объекты по возрастанию вероятностей (RF), разобьем на kравных частей и для каждой части вычислим среднее всех ответов алгоритма и среднее всех правильных ответов. Результат показан на рис. 5 – точки изображены как раз в этих двух координатах.

Нетрудно видеть, что точки располагаются на линии, похожей на сигмоиду – можно оценить параметр сжатия-растяжения в ней, см. рис. 6. Оптимальная сигмоида показана розовым цветом на рис. 5. Если подвергать ответы такой сигмоидной деформации, то логлосс-ошибка случайного леса снижается с 0.37 до 0.33.

Обратите внимание, что здесь мы деформировали ответы случайного леса (это были оценки вероятности – и все они лежали на отрезке [0, 1]), но из рис. 5 видно, что для деформации нужна именно сигмоида. Практика показывает, что в 80% ситуаций для улучшения logloss-ошибки надо деформировать ответы именно с помощью сигмоиды (для меня это также часть объяснения, почему именно такие функции успешно используются в качестве функций активаций в нейронных сетях).

Ещё один вариант калибровки – монотонная регрессия (Isotonic regression).

Многоклассовый logloss

Для полноты картины отметим, что logloss обобщается и на случай нескольких классов естественным образом:

здесь q – число элементов в выборке, l – число классов, a_ij – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности его к j-му классу, y_ij=1 если i-й объект принадлежит j-му классу, в противном случае y_ij=0.

Источник: m.vk.com

Комментарии: