Линейная регрессия на Python: объясняем на пальцах

2019-04-25 22:00

разработка по, алгоритмы машинного обучения

Линейная регрессия применяется для анализа данных и в машинном обучении. Постройте свою модель на Python и получите первые результаты!

Линейная регрессия на Python: объясняем на пальцах

Регрессия ищет отношения между переменными.

Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.

Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.

Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.

Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.

Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.

Зависимые данные называются зависимыми переменными, выходами или ответами.

Независимые данные называются независимыми переменными, входами или предсказателями.

Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.

Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (??, …, ??), где ? – количество входных переменных.

Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.

Где она вообще нужна?

Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.

Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.

Постановка проблемы

Линейная регрессия некоторой зависимой переменной ? на набор независимых переменных ? = (??, …, ??), где ? – это число предсказателей, предполагает, что линейное отношение между ? и ?: ? = ?? + ???? + ? + ???? + ?. Это уравнение регрессии. ??, ??, …, ?? – коэффициенты регрессии, и ? – случайная ошибка.

Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как ??, ??, …, ??. Они определяют оценочную функцию регрессии ?(?) = ?? + ???? + ? + ????. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.

Для каждого результата наблюдения ? = 1, …, ?, оценочный или предсказанный ответ ?(??) должен быть как можно ближе к соответствующему фактическому ответу ??. Разницы от ?? ? ?(??) для всех результатов наблюдений ? = 1, …, ? называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.

Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений ? = 1, …, ?: SSR = ??(?? ? ?(??))?. Этот подход называется методом наименьших квадратов.

Простая линейная регрессия

Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной ? = ?.

А вот и она:

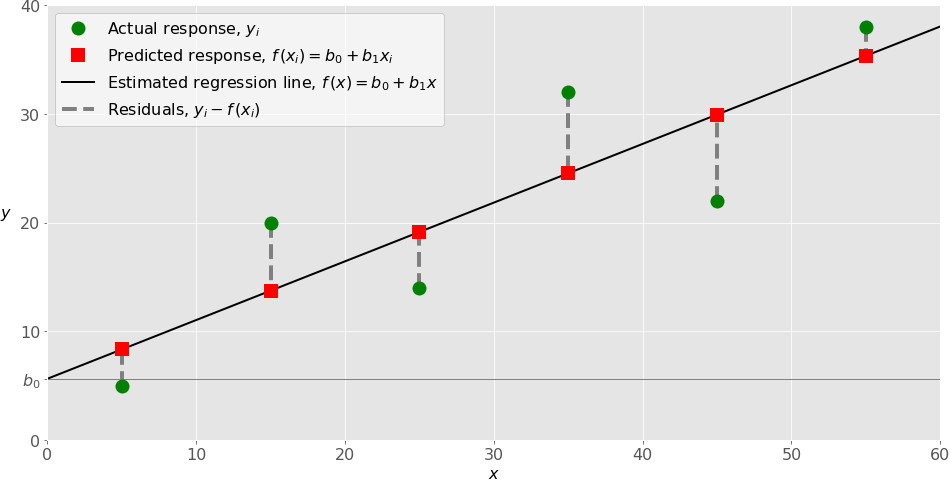
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (?-?). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе ? = 5 и соответствующий выход (ответ) ? = 5. Следующее наблюдение имеет ? = 15 и ? = 20, и так далее.

Оценочная функция регрессии (чёрная линия) выражается уравнением ?(?) = ?? + ???. Нужно рассчитать оптимальные значения спрогнозированных весов ?? и ?? для минимизации SSR и определить оценочную функцию регрессии. Величина ??, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось ?. Это значение расчётного ответа ?(?) для ? = 0. Величина ?? определяет наклон расчетной линии регрессии.

Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа ? = 5 предсказанный ответ равен ?(5) = 8.33 (представленный крайним левыми квадратом).

Остатки (вертикальные пунктирные серые линии) могут быть вычислены как ?? ? ?(??) = ?? ? ?? ? ???? для ? = 1, …, ?. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.

Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.

Пакеты Python для линейной регрессии

NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.

Незнакомы с NumPy? Начните с официального гайда.

Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.

Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.

Простая линейная регрессия со scikit-learn

Начнём с простейшего случая линейной регрессии.

Следуйте пяти шагам реализации линейной регрессии:

Импортируйте необходимые пакеты и классы.
Предоставьте данные для работы и преобразования.
Создайте модель регрессии и приспособьте к существующим данным.
Проверьте результаты совмещения и удовлетворительность модели.
Примените модель для прогнозов.

Это общие шаги для большинства подходов и реализаций регрессии.

Шаг 1: Импортируйте пакеты и классы

Первым шагом импортируем пакет NumPy и класс LinearRegressionиз sklearn.linear_model:

Python

1 2	importnumpy asnp fromsklearn.linear_model importLinearRegression

Теперь у вас есть весь функционал для реализации линейной регрессии.

Фундаментальный тип данных NumPy – это тип массива numpy.ndarray. Далее под массивом подразумеваются все экземпляры типа numpy.ndarray.

Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.

Шаг 2 : Предоставьте данные

Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, ?) и выход (предсказатель, ?) должны быть массивами (экземпляры класса numpy.ndarray) или похожими объектами. Вот простейший способ предоставления данных регрессии:

Python

1 2	x=np.array([5,15,25,35,45,55]).reshape((-1,1)) y=np.array([5,20,14,32,22,38])

Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape()на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).

Вот как x и y выглядят теперь:

Python

>>>print(x)

[[5]

[15]

[25]

[35]

[45]

[55]]

>>>print(y)

[52014322238]

Шаг 3: Создайте модель

На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.

Давайте сделаем экземпляр класса LinearRegression, который представит модель регрессии:

Python

1	model=LinearRegression()

Эта операция создаёт переменную model в качестве экземпляра LinearRegression. Вы можете предоставить несколько опциональных параметров классу LinearRegression:

fit_intercept – логический (True по умолчанию) параметр, который решает, вычислять отрезок ?? (True) или рассматривать его как равный нулю (False).
normalize – логический (False по умолчанию) параметр, который решает, нормализовать входные переменные (True) или нет (False).
copy_X – логический (True по умолчанию) параметр, который решает, копировать (True) или перезаписывать входные переменные (False).
n_jobs – целое или None (по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях. None означает отсутствие процессов, при -1 используются все доступные процессоры.

Наш пример использует состояния параметров по умолчанию.

Пришло время задействовать model. Сначала вызовите .fit() на model:

Python

1	model.fit(x,y)

С помощью .fit() вычисляются оптимальные значение весов ?? и ??, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self — переменную model. Поэтому можно заменить две последние операции на:

Python

1	model=LinearRegression().fit(x,y)

Эта операция короче и делает то же, что и две предыдущие.

Шаг 4: Получите результаты

После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.

Вы можете получить определения (??) с помощью .score(), вызванной на model:

Python

>>>r_sq=model.score(x,y)

>>>print('coefficient of determination:',r_sq)

coefficient of determination:0.715875613747954

.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение ??.

model содержит атрибуты .intercept_, который представляет собой коэффициент, и ?? с .coef_, которые представляют ??:

Python

>>>print('intercept:',model.intercept_)

intercept:5.633333333333329

>>>print('slope:',model.coef_)

slope:[0.54]

Код выше показывает, как получить ?? и ??. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.

Примерное значение ?? = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при ?, равным нулю. Равенство ?? = 0.54 означает, что предсказанный ответ возрастает до 0.54 при ?, увеличенным на единицу.

Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:

Python

>>>new_model=LinearRegression().fit(x,y.reshape((-1,1)))

>>>print('intercept:',new_model.intercept_)

intercept:[5.63333333]

>>>print('slope:',new_model.coef_)

slope:[[0.54]]

Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом ??, и .coef_ – двумерный массив с единственным элементом ??.

Шаг 5: Предскажите ответ

Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.

Получите предсказанный ответ, используя .predict():

Python

>>>y_pred=model.predict(x)

>>>print('predicted response:',y_pred,sep=' ')

predicted response:

[8.3333333313.7333333319.1333333324.5333333329.9333333335.33333333]

Применяя .predict(), вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.

Вот почти идентичный способ предсказать ответ:

Python

>>>y_pred=model.intercept_+model.coef_*x

>>>print('predicted response:',y_pred,sep=' ')

predicted response:

[[8.33333333]

[13.73333333]

[19.13333333]

[24.53333333]

[29.93333333]

[35.33333333]]

В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.

Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.

Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1), x.flatten() или x.ravel() при умножении с помощью model.coef_.

На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:

Python

>>>x_new=np.arange(5).reshape((-1,1))

>>>print(x_new)

[[0]

[1]

[2]

[3]

[4]]

>>>y_new=model.predict(x_new)

>>>print(y_new)

[5.633333336.173333336.713333337.253333337.79333333]

Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new. Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.

О LinearRegression вы узнаете больше из официальной документации.

Теперь у вас есть своя модель линейной регрессии!

Источник: proglib.io

Линейная регрессия на Python: объясняем на пальцах

Комментарии: