Венгерский алгоритм, или о том, как математика помогает в распределении назначений

В этой статье хотел бы рассказать про интересный алгоритм из дисциплины «Исследование операций» а именно про Венгерский метод и как с его помощью решать задачи о назначениях. Немного затрону теории про то, в каких случаях и для каких задач применим данный алгоритм, поэтапно разберу его на мною выдуманном примере, и поделюсь своим скромным наброском кода его реализации на языке R. Приступим!

Пару слов о методе

Для того чтобы не расписывать много теории с математическими терминами и определениями, предлагаю рассмотреть пару вариантов построения задачи о назначениях, и я думаю Вы сразу поймете в каких случаях применим Венгерский метод:

• Задача о назначении работников на должности. Необходимо распределить работников на должности так, чтобы достигалась максимальная эффективность, или были минимальные затраты на работу.
• Назначение машин на производственные секции. Распределение машин так, чтобы при их работе производство было максимально прибыльным, или затраты на их содержание минимальны.
• Выбор кандидатов на разные вакансии по оценкам. Этот пример разберем ниже.

Как Вы видите, вариантов для которых применим Венгерский метод много, при этом подобные задачи возникают во многих сферах деятельности.

В итоге задача должна быть решена так, чтобы один исполнитель (человек, машина, орудие, …) мог выполнять только одну работу, и каждая работа выполнялась только одним исполнителем.

Необходимое и достаточное условие решения задачи – это ее закрытый тип. Т.е. когда количество исполнителей = количеству работ (N=M). Если же это условие не выполняется, то можно добавить вымышленных исполнителей, или вымышленные работы, для которых значения в матрице будут нулевыми. На решение задачи это никак не повлияет, лишь придаст ей тот необходимый закрытый тип.

Step-by-step алгоритм на примере

Постановка задачи: Пусть намечается важная научная конференция. Для ее проведения необходимо настроить звук, свет, изображения, зарегистрировать гостей и подготовиться к перерывам между выступлениями. Для этой задачи есть 5 организаторов. Каждый из них имеет определенные оценки выполнения той, или иной работы (предположим, что эти оценки выставлены как среднее арифметическое по отзывам их сотрудников). Необходимо распределить организаторов так, чтобы суммарная их оценка была максимальной. Задача имеет следующий вид:

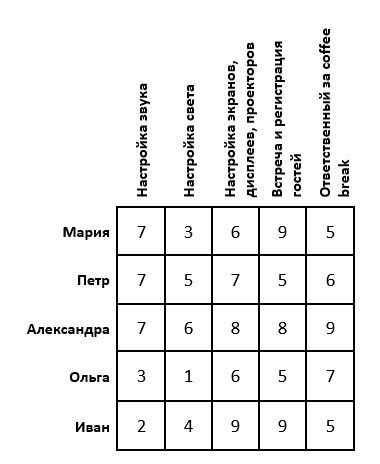
Если задача решается на максимум (как в нашем случае), то в каждой строке матрицы необходимо найти максимальный элемент, его же вычесть из каждого элемента соответствующей строки и умножить всю матрицу на -1. Если задача решается на минимум, то этот шаг необходимо пропустить.

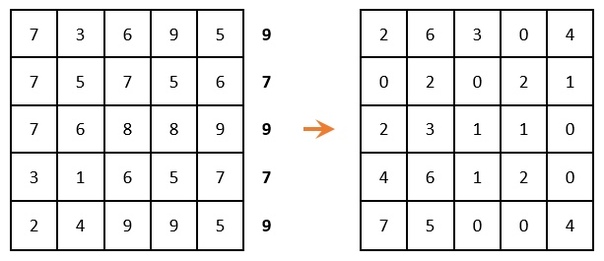
В каждой строке и в каждом столбце должен быть только один выбранный ноль. (т.е. когда выбрали ноль, то остальные нули в этой строке или в этом столбце уже не берем в расчет). В этом случае это сделать невозможно:

(Если задача решается на минимум, то необходимо начинать с этого шага). Продолжаем решение далее. Редукция матрицы по строкам (ищем минимальный элемент в каждой строке и вычитаем его из каждого элемента соответственно):

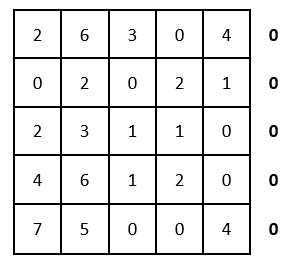
Т.к. все минимальные элементы – нулевые, то матрица не изменилась. Проводим редукцию по столбцам:

Опять же смотрим чтобы в каждом столбце и в каждой строке был только один выбранный ноль. Как видно ниже, в данном случае это сделать невозможно. Представил два варианта как можно выбрать нули, но ни один из них не дал нужный результат:

Продолжаем решение дальше. Вычеркиваем строки и столбцы, которые содержат нулевые элементы (ВАЖНО! Количество вычеркиваний должно быть минимальным). Среди оставшихся элементов ищем минимальный, вычитаем его из оставшихся элементов (которые не зачеркнуты) и прибавляем к элементам, которые расположены на пересечении вычеркнутых строк и столбцов (то, что отмечено зеленым – там вычитаем; то, что отмечено золотистым – там суммируем; то, что не закрашено – не трогаем):

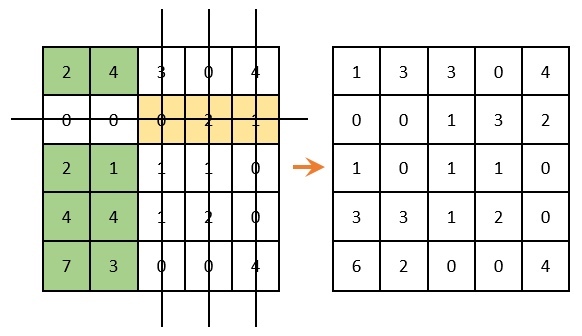
Как теперь видно, в каждом столбце и строке есть только один выбранный ноль. Решение задачи завершаем!

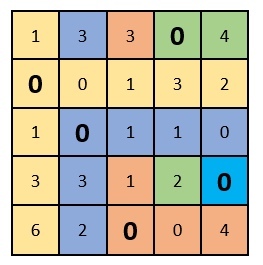
Подставляем в начальную таблицу месторасположения выбранных нулей. Таким образом мы получаем оптимум, или оптимальный план, при котором организаторы распределены по работам и сумма оценок получилась максимальной:

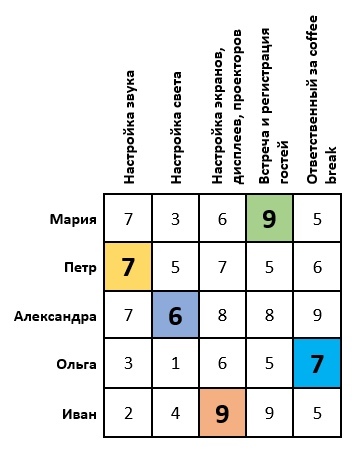
Если же вы решаете задачу и у вас до сих пор невозможно выбрать нули так, чтобы в каждом столбце и строке был только один, тогда повторяем алгоритм с того места где проводилась редукция по строкам (минимальный элемент в каждой строке).

Реализация на языке программирования R

Венгерский алгоритм реализовал с помощью рекурсий. Буду надеяться что мой код не будет вызывать трудностей. Для начала необходимо скомпилировать три функции, а затем начинать расчеты.

Данные для решения задачи берутся из файла example.csv который имеет вид:

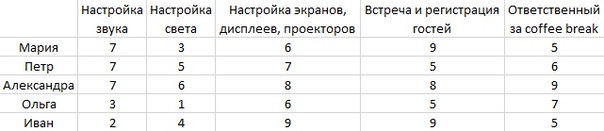
Код:

#Подключаем библиотеку для удобства расчетов library(dplyr)  #Считываем csv фаил (первый столбик - названия строк; первая строка - названия столбцов) table <- read.csv("example.csv",header=TRUE,row.names=1,sep=";")  #Проводим расчеты unique_index <- hungarian_algorithm(table,T)  #Выводим cat(paste(row.names(table[as.vector(unique_index$row),])," - ",names(table[as.vector(unique_index$col)])),sep = " ")  #Считаем оптимальный план cat("Оптимальное значение -",sum(mapply(function(i, j) table[i, j], unique_index$row, unique_index$col, SIMPLIFY = TRUE)))    #____________________Алгоритм венгерского метода__________________________________  hungarian_algorithm <- function(data,optim=F){    #Если optim = T, то будет искаться максимальное оптимальное значение   if(optim==T)   {     data <- data %>%        apply(1,function(x) (x-max(x))*(-1)) %>%        t() %>%        as.data.frame()     optim <- F   }    #Редукция матрицы по строкам   data <- data %>%     apply(1,function(x) x-min(x)) %>%      t() %>%      as.data.frame()    #Нахождение индексов всех нулей   zero_index <- which(data==0, arr.ind = T)    #Нахождение всех "неповторяющихся" нулей слева-направо   unique_index <- from_the_beginning(zero_index)    #Если количество "неповторяющихся" нулей не равняется количеству строк в исходной таблице, то..   if(nrow(unique_index)!=nrow(data)) #..Ищем "неповторяющиеся" нули справа-налево     unique_index <- from_the_end(zero_index)    #Если все еще не равняется, то продолжаем алгоритм дальше   if(nrow(unique_index)!=nrow(data))   {      #Редукция матрицы по столбцам     data <- data %>%       apply(2,function(x) x-min(x)) %>%        as.data.frame()          zero_index <- which(data==0, arr.ind = T)     unique_index <- from_the_beginning(zero_index)          if(nrow(unique_index)!=nrow(data))       unique_index <- from_the_end(zero_index)          if(nrow(unique_index)!=nrow(data))     {        #"Вычеркиваем" строки и столбцы которые содержат нулевые элементы (ВАЖНО! количество вычеркиваний должно быть минимальным)       index <- which(apply(data,1,function(x) length(x[x==0])>1))       index2 <- which(apply(data[-index,],2,function(x) length(x[x==0])>0))        #Среди оставшихся элементов ищем минимальный       min_from_table <- min(data[-index,-index2])        #Вычитаем минимальный из оставшихся элементов       data[-index,-index2] <- data[-index,-index2]-min_from_table        #Прибавляем к элементам, расположенным на пересечении вычеркнутых строк и столбцов       data[index,index2] <- data[index,index2]+min_from_table              zero_index <- which(data==0, arr.ind = T)       unique_index <- from_the_beginning(zero_index)              if(nrow(unique_index)!=nrow(data))         unique_index <- from_the_end(zero_index)        #Если все еще количество "неповторяющихся" нулей не равняется количеству строк в исходной таблице, то..       if(nrow(unique_index)!=nrow(data)) #..Повторяем весь алгоритм заново         hungarian_algorithm(data,optim)              else #Выводим индексы "неповторяющихся" нулей         unique_index     }     else #Выводим индексы "неповторяющихся" нулей       unique_index   }   else #Выводим индексы "неповторяющихся" нулей     unique_index } #_________________________________________________________________________________   #__________Функция для нахождения "неповторяющихся" нулей слева-направо___________  from_the_beginning <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){    #Выбор индексов нулей, которые не лежат на строках i, и столбцах j   find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),]      if(length(find_zero)>2){      #Записываем индекс строки в вектор     i <- c(i,as.vector(find_zero[1,1]))    #Записываем индекс столбца в вектор     j <- c(j,as.vector(find_zero[1,2]))      #Записываем индексы в data frame (это и есть индексы уникальных нулей)     index <- rbind(index,setNames(as.list(find_zero[1,]), names(index)))      #Повторяем пока не пройдем по всем строкам и столбцам     from_the_beginning(find_zero,i,j,index)}   else     rbind(index,find_zero) } #_________________________________________________________________________________  #__________Функция для нахождения "неповторяющихся" нулей справа-налево___________  from_the_end <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){   find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),]   if(length(find_zero)>2){     i <- c(i,as.vector(find_zero[nrow(find_zero),1]))     j <- c(j,as.vector(find_zero[nrow(find_zero),2]))     index <- rbind(index,setNames(as.list(find_zero[nrow(find_zero),]), names(index)))     from_the_end(find_zero,i,j,index)}   else     rbind(index,find_zero) } #_________________________________________________________________________________  

Результат выполнения программы:

Источник: habr.com

Комментарии: