Пишем XGBoost с нуля — часть 2: градиентный бустинг

В прошлой статье мы разбирались, как устроены решающие деревья, и с нуля реализовали алгоритм построения, попутно оптимизируя и улучшая его. В этой статье мы реализуем алгоритм градиентного бустинга и в конце создадим свой собственный XGBoost. Повествование будет идти по той же схеме: пишем алгоритм, описываем его, в заверешение подводим итоги, сравнивая результаты работы с аналогами из Sklearn'а. В этой статье упор тоже будет сделан на реализацию в коде, поэтому всю теорию лучше почитать в другом вместе (например, в курсе ODS), и уже со знанием теории можно переходить к этой статье, так как тема достаточно сложная.

Что такое градиентный бустинг? Картинка с гольфистом как нельзя лучше описывает основную идею. Для того, что загнать мяч в лунку, гольфист делает каждый следующий удар с учётом опыта предыдущих ударов — для него это необходимое условие, чтобы загнать мяч в лунку. Еслиочень грубо (я не мастер игры в гольф :)), то при каждом новом ударе первое, на что смотрит гольфист, это на расстояние между мячом и лункой после предыдущего удара. И основная задача — следующим ударом уменьшить это расстояние. Бустинг строится очень похожим способом. Во-первых, нам нужно ввести определение «лунки», то есть цели, к которой мы будем стремиться. Во-вторых, нам нужно научится понимать, в какую сторону нужно бить клюшкой, чтобы попасть ближе к цели. В-третьих, с учётом всех этих правил нужно придумать правильную последовательность ударов, чтобы каждый последующий сокращал расстояние между мячом и лункой.

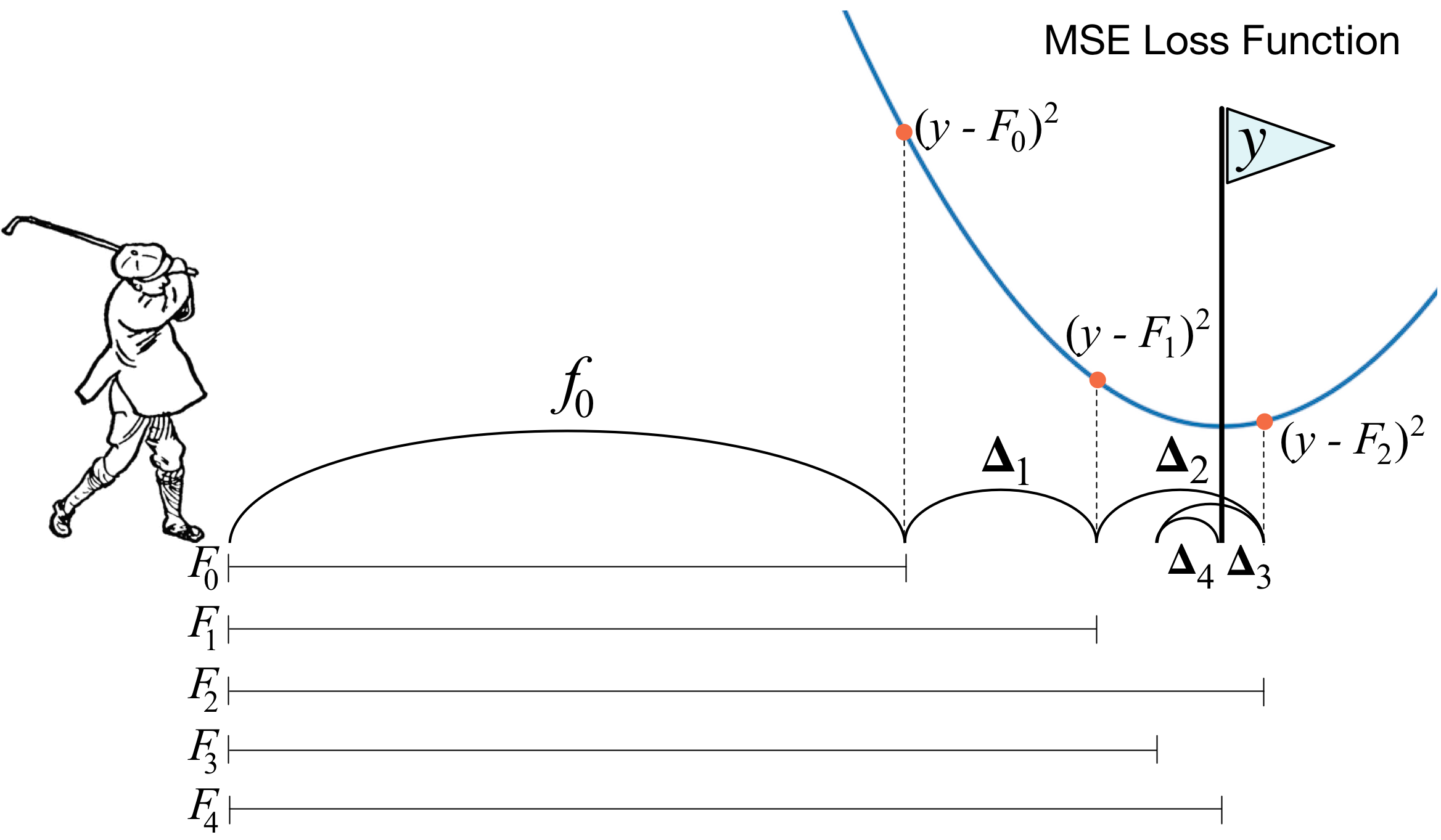
Теперь дадим чуть более строгое определение. Введём модель взвешенного голосования:

$$

Здесь $$ — это пространство, из которого берём объекты, $$ — это коэффицент перед моделью и непосредственно сама модель, то есть дерево решений. Допустим, что уже на каком-то шаге с помощью описанных правил удалось добавить в композицию $$ слабый алгоритм. Чтобы научиться понимать, какой-именно должен быть алгоритм на шаге $$, введем функцию ошибки:

$$ Получается, что наилучшим алгоритмом будет тот, который сможет максимально уменьшать ошибку, полученную на предыдущих итерациях. И так как бустинг градиентный, то у этой функции ошибки обязательно должен существовать вектор антиградиента, вдоль которого можно двигаться в поисках минимума. Всё!

Непосредственно перед реализацией вставлю ещё пару слов о том, как именно у нас всё будет устроено. Как и в прошлой статье, в качестве лосса возьмем MSE. Посчитаем её градиент:

$$

Таким образом, вектор антиградиента будет равен $$. На шаге $$ мы считаем ошибки алгоритма, полученного на прошлых итерациях. Далее обучаем наш новый алгоритм на этих ошибках, а затем со знаком минус и каким-то коэффициентом добавляем к нашему ансамблю.

Теперь приступим к реализации.

1. Реализация обычного класса градиентного бустинга

import pandas as pd import matplotlib.pyplot as plt import numpy as np from tqdm import tqdm_notebook from sklearn import datasets from sklearn.metrics import mean_squared_error as mse from sklearn.tree import DecisionTreeRegressor import itertools %matplotlib inline  %load_ext Cython  %%cython -a   import itertools import numpy as np cimport numpy as np from itertools import *  cdef class RegressionTreeFastMse:          cdef public int max_depth     cdef public int feature_idx     cdef public int min_size     cdef public int averages           cdef public np.float64_t feature_threshold     cdef public np.float64_t value      cpdef RegressionTreeFastMse left     cpdef RegressionTreeFastMse right          def __init__(self, max_depth=3, min_size=4, averages=1):                  self.max_depth = max_depth         self.min_size = min_size         self.value = 0         self.feature_idx = -1         self.feature_threshold = 0         self.left = None         self.right = None          def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y):          cpdef np.float64_t mean1 = 0.0         cpdef np.float64_t mean2 = 0.0         cpdef long N = X.shape[0]         cpdef long N1 = X.shape[0]         cpdef long N2 = 0         cpdef np.float64_t delta1 = 0.0         cpdef np.float64_t delta2 = 0.0         cpdef np.float64_t sm1 = 0.0         cpdef np.float64_t sm2 = 0.0         cpdef list index_tuples         cpdef list stuff         cpdef long idx = 0                  cpdef np.float64_t prev_error1 = 0.0         cpdef np.float64_t prev_error2 = 0.0         cpdef long thres = 0         cpdef np.float64_t error = 0.0                  cpdef np.ndarray[long, ndim=1] idxs                  cpdef np.float64_t x = 0.0                      # начальное значение - среднее значение y         self.value = y.mean()         # начальная ошибка - mse между значением в листе          base_error = ((y - self.value) ** 2).sum()         error = base_error         flag = 0                  # пришли на максимальную глубину         if self.max_depth <= 1:             return              dim_shape = X.shape[1]                  left_value, right_value = 0, 0                  for feat in range(dim_shape):                          prev_error1, prev_error2 = base_error, 0              idxs = np.argsort(X[:, feat])                          # переменные для быстрого переброса суммы             mean1, mean2 = y.mean(), 0             sm1, sm2 = y.sum(), 0                          N = X.shape[0]             N1, N2 = N, 0             thres = 1                          while thres < N - 1:                 N1 -= 1                 N2 += 1                  idx = idxs[thres]                 x = X[idx, feat]                                  # вычисляем дельты - по ним, в основном, будет делаться переброс                 delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1                 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2                  # увеличиваем суммы                 sm1 -= y[idx]                 sm2 += y[idx]                                  # пересчитываем ошибки за O(1)                 prev_error1 += (delta1**2) * N1                  prev_error1 -= (y[idx] - mean1)**2                  prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1)                 mean1 = sm1/N1                                  prev_error2 += (delta2**2) * N2                  prev_error2 += (y[idx] - mean2)**2                  prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2)                 mean2 = sm2/N2                                  # пропускаем близкие друг к другу значения                 if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5:                     thres += 1                     continue                                  if (prev_error1 + prev_error2 < error):                     if (min(N1,N2) > self.min_size):                                              # переопределяем самый лучший признак и границу по нему                         self.feature_idx, self.feature_threshold = feat, x                         # переопределяем значения в листах                         left_value, right_value = mean1, mean2                          # флаг - значит сделали хороший сплит                         flag = 1                         error = prev_error1 + prev_error2                                                       thres += 1                  # ничего не разделили, выходим         if self.feature_idx == -1:             return                  # вызываем потомков дерева         self.left = RegressionTreeFastMse(self.max_depth - 1)         self.left.value = left_value         self.right = RegressionTreeFastMse(self.max_depth - 1)         self.right.value = right_value                  # новые индексы для обучения потомков         idxs_l = (X[:, self.feature_idx] > self.feature_threshold)         idxs_r = (X[:, self.feature_idx] <= self.feature_threshold)                  # обучение потомков         self.left.fit(X[idxs_l, :], y[idxs_l])         self.right.fit(X[idxs_r, :], y[idxs_r])              def __predict(self, np.ndarray[np.float64_t, ndim=1] x):                  if self.feature_idx == -1:             return self.value                  if x[self.feature_idx] > self.feature_threshold:             return self.left.__predict(x)         else:             return self.right.__predict(x)              def predict(self, np.ndarray[np.float64_t, ndim=2] X):                      y = np.zeros(X.shape[0])         for i in range(X.shape[0]):             y[i] = self.__predict(X[i])                      return y

class GradientBoosting():          def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3,                   random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'):                      self.n_estimators = n_estimators         self.max_depth = max_depth         self.learning_rate = learning_rate         self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]])         self.min_size = min_size         self.loss_by_iter = []         self.trees_ = []         self.loss_by_iter_test = []         self.n_samples = n_samples         self.base_tree = base_tree           def fit(self, X, y):         self.X = X         self.y = y         b = self.initialization(y)                  prediction = b.copy()                  for t in tqdm_notebook(range(self.n_estimators)):                                         if t == 0:                 resid = y             else:                 # сразу пишем антиградиент                 resid = (y - prediction)                          # выбираем базовый алгоритм             if self.base_tree == 'Bagging':                 tree = Bagging(max_depth=self.max_depth,                                        min_size = self.min_size)                             if self.base_tree == 'Tree':                 tree = RegressionTreeFastMse(max_depth=self.max_depth,                                           min_size = self.min_size)                              # обучаемся на векторе антиградиента             tree.fit(X, resid)             # делаем предикт и добавляем алгоритм к ансамблю             b = tree.predict(X).reshape([X.shape[0]])             self.trees_.append(tree)             prediction += self.learning_rate * b             # добавляем только если не первая итерация             if t > 0:                 self.loss_by_iter.append(mse(y,prediction))                             return self          def predict(self, X):                  # сначала прогноз – это просто вектор из средних значений ответов на обучении         pred = np.ones([X.shape[0]]) * np.mean(self.y)         # добавляем прогнозы деревьев         for t in range(self.n_estimators):             pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]])                      return pred     

Построим теперь кривую лосса на обучающей выборке, чтобы убедиться, что при каждой итерации у нас действительно происходит его уменьшение.

GDB = GradientBoosting(n_estimators=50) GDB.fit(X,y) x = GDB.predict(X) plt.grid() plt.title('Loss by iterations') plt.plot(GDB.loss_by_iter)

2. Бэггинг над решающими деревьями

Отлично, перед тем как сравнивать результаты, давайте поговорим ещё и о процедуре бэггинга над деревьями. Тут вс просто: мы хотим защититься от переобучения, и поэтому с помощью выборок с возращением будем усреднять наши предсказания, чтобы случайно не напороться на выбросы (почему это так работает — лучше почитайте по ссылке).

class Bagging():          '''     Класс Bagging - предназначен для генерирования бустрапированного     выбора моделей.     '''          def __init__(self, max_depth = 3, min_size=10, n_samples = 10):                      #super(CART, self).__init__()         self.max_depth = max_depth         self.min_size = min_size         self.n_samples = n_samples         self.subsample_size = None         self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth,                                  min_size=self.min_size) for _ in range(self.n_samples)]      def get_bootstrap_samples(self, data_train, y_train):                  # генерируем индексы выборок с возращением         indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size))         samples_train = data_train[indices]         samples_y = y_train[indices]         return samples_train, samples_y          def fit(self, data_train, y_train):                  # обучаем каждую модель          self.subsample_size = int(data_train.shape[0])         samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train)         for i in range(self.n_samples):             self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1))         return self              def predict(self, test_data):                  # для каждого объекта берём его средний предикт         num_samples = test_data.shape[0]         pred = []         for i in range(self.n_samples):             pred.append(self.list_of_Carts[i].predict(test_data))         pred = np.array(pred).T          return np.array([np.mean(pred[i]) for i in range(num_samples)])     

Отлично, теперь в качестве базового алгоритма можем использовать не одно дерево, а бэггинг из деревьев — так мы, опять же, защитимся от переобучения.

3. Результаты

Сравним результаты наших алгоритмов.

from sklearn.model_selection import KFold import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn import copy  def get_metrics(X,y,n_folds=2, model=None):     kf = KFold(n_splits=n_folds, shuffle=True)     kf.get_n_splits(X)      er_list = []     for train_index, test_index in tqdm_notebook(kf.split(X)):         X_train, X_test = X[train_index], X[test_index]         y_train, y_test = y[train_index], y[test_index]         model.fit(X_train,y_train)         predict = model.predict(X_test)         er_list.append(mse(y_test, predict))          return er_list  data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' )) er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' )) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1))  %matplotlib inline data = [er_sklearn_boosting, er_boosting, er_boobagg] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag']) plt.grid() plt.show()

Получили:

Мы пока не можем победить аналог из Sklearn, потому что опять не учитываем очень много параметров, которые используются в этом методе. Однако мы видим, что бэггинг чуть-чуть помогает. Не будем отчаиваться, и перейдём к написанию XGBoost'а.

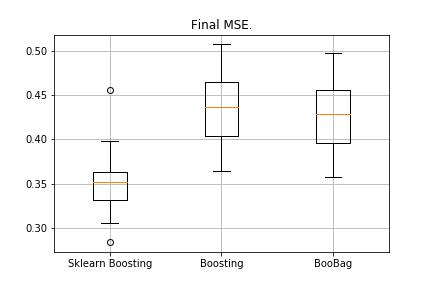
4. XGBoost

Прежде чем читать дальше, очень советую сначала ознакомиться со следующим видео, в нём очень хорошо объясняется теория. Вспомним, какую ошибку мы минимизируем в обычном бустинге:

$$

XGBoost явно добавляет регуляризацию в этот функционал ошибки:

$$

Как считать этот функционал? Сначала приближаем его с помощью ряда Тейлора второго порядка, где новый алгоритм рассматривается как приращение, вдоль которого мы будем двигаться, и дальше уже расписываем в зависимости от того, какой у нас лосс:
$$ Необходимо определить, какое дерево мы будем считать плохим, а какое хорошим.

Вспомним, на каком принципе построена с регрессия с $$-регуляризацией — чем больше по норме значения коэффициентов перед регрессией, тем хуже, поэтому нужно, чтобы они были как можно меньше.

В XGBoost идея очень похожа: дерево штрафуется, если сумма нормы значений в листьях в нём очень большая. Поэтому сложность дерева здесь вводится следующим образом:

$$

$$ — значения в листьях, $$ — количество листьев.

В видео есть переходные формулы, мы их здесь выводить не будем. Всё сводится к тому, что новое разбиение мы будем выбирать, максимизируя gain:

$$

Здесь $$ — это числовые параметры регуляризации, а $$ — соответствующие суммы из первых и вторых производных при данном разбиении.

Всё, теория очень кратко изложена, ссылки даны, теперь поговорим, какими будут производные, если мы работает с MSE. Всё просто:

$$ Когда будем считать суммы $$, к первой просто прибавляем $$, а ко второй — просто количество.

%%cython -a   import numpy as np cimport numpy as np  cdef class RegressionTreeGain:     cdef public int max_depth     cdef public np.float64_t gain     cdef public np.float64_t lmd     cdef public np.float64_t gmm          cdef public int feature_idx     cdef public int min_size      cdef public np.float64_t feature_threshold     cdef public np.float64_t value          cpdef public RegressionTreeGain left     cpdef public RegressionTreeGain right          def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5):         self.max_depth = max_depth         self.gmm = gmm         self.lmd = lmd         self.left = None         self.right = None         self.feature_idx = -1         self.feature_threshold = 0         self.value = -1e9         self.min_size = min_size                  return          def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y):                  cpdef long N = X.shape[0]         cpdef long N1 = X.shape[0]         cpdef long N2 = 0         cpdef long idx = 0         cpdef long thres = 0         cpdef np.float64_t gl, gr, gn         cpdef np.ndarray[long, ndim=1] idxs         cpdef np.float64_t x = 0.0         cpdef np.float64_t best_gain = -self.gmm                  if self.value == -1e9:             self.value = y.mean()                  base_error = ((y - self.value) ** 2).sum()         error = base_error         flag = 0                  if self.max_depth <= 1:             return                  dim_shape = X.shape[1]                  left_value = 0         right_value = 0                  # начинаем процесс обучения         # чуть-чуть матана - у нас mse, L = (y - pred)**2         # dL/dpred = pred - y, эту разницу мы в бустинге будем передавать со знаком -         # dL^2/d^2pred = 1 - получается, это просто количество объектов в листе                  for feat in range(dim_shape):                          idxs = np.argsort(X[:, feat])                           gl,gr = y.sum(),0.0              N1, N2, thres = N, 0, 0                          while thres < N - 1:                 N1 -= 1                 N2 += 1                  idx = idxs[thres]                 x = X[idx, feat]                                  gl -= y[idx]                 gr += y[idx]                                  # считаем гейн                 gn = (gl**2) / (N1 + self.lmd)  + (gr**2) / (N2 + self.lmd)                 gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm                                  if thres < N - 1 and x == X[idxs[thres + 1], feat]:                     thres += 1                     continue                                  # проверяем условия на гейн                 if (gn > best_gain) and (min(N1,N2) > self.min_size):                                          flag = 1                     best_gain = gn                     left_value = -gl / (N1 + self.lmd)                     right_value = -gr / (N2 + self.lmd)                                          self.feature_idx = feat                     self.feature_threshold = x                  thres += 1                  self.gain = best_gain         if self.feature_idx == -1:             return                          self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd)         self.left.value = left_value         self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd)         self.right.value = right_value                  idxs_l = (X[:, self.feature_idx] > self.feature_threshold)         idxs_r = (X[:, self.feature_idx] <= self.feature_threshold)              self.left.fit(X[idxs_l, :], y[idxs_l])         self.right.fit(X[idxs_r, :], y[idxs_r])                  # подрубаем отрицательный гейн         if (self.left.left == None or self.right.left == None):             if self.gain < 0.0:                 self.left = None                 self.right = None                 self.feature_idx = -1      def __predict(self, np.ndarray[np.float64_t, ndim=1] x):         if self.feature_idx == -1:             return self.value                  if x[self.feature_idx] > self.feature_threshold:              return self.left.__predict(x)         else:             return self.right.__predict(x)              def predict(self, np.ndarray[np.float64_t, ndim=2] X):         y = np.zeros(X.shape[0])                  for i in range(X.shape[0]):             y[i] = self.__predict(X[i])                      return y

Небольшое уточнение: чтобы формулы в деревьях с gain'ом были красивее, в бустинге обучаем таргет со знаком минус.

Слегка модифицируем наш бустинг, сделаем некоторые параметры адаптивными. Например, если замечаем, что лосс начал выходить на плато, то уменьшаем learning rate и увеличиваем max_depth у следующих эстиматоров. Также добавим новый бэггинг — теперь сделаем бустинг над бэггингами из деревьев с gain'ом:

class Bagging():          def __init__(self, max_depth = 3, min_size=5, n_samples = 10):                      self.max_depth = max_depth         self.min_size = min_size         self.n_samples = n_samples         self.subsample_size = None         self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth,                                  min_size=self.min_size) for _ in range(self.n_samples)]           def get_bootstrap_samples(self, data_train, y_train):                  indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size))         samples_train = data_train[indices]         samples_y = y_train[indices]         return samples_train, samples_y          def fit(self, data_train, y_train):                  self.subsample_size = int(data_train.shape[0])         samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train)         for i in range(self.n_samples):             self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1))         return self              def predict(self, test_data):                  num_samples = test_data.shape[0]         pred = []         for i in range(self.n_samples):             pred.append(self.list_of_Carts[i].predict(test_data))         pred = np.array(pred).T          return np.array([np.mean(pred[i]) for i in range(num_samples)])

class GradientBoosting():           def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3,                   random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'):                      self.n_estimators = n_estimators         self.max_depth = max_depth         self.learning_rate = learning_rate         self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]])         self.min_size = min_size         self.loss_by_iter = []         self.trees_ = []         self.loss_by_iter_test = []         self.n_samples = n_samples         self.base_tree = base_tree          # хотим как-то регулировать работу алгоритма на поздних итерациях         # если ошибка застряла, то уменьшаем lr и увеличиваем max_depth         self.add_to_max_depth = 1         self.init_mse_board = 1.5          def fit(self, X, y):         print (self.base_tree)         self.X = X         self.y = y         b = self.initialization(y)                  prediction = b.copy()                  for t in tqdm_notebook(range(self.n_estimators)):                                      if t == 0:                 resid = y             else:                 resid = (y - prediction)                 if (mse(temp_resid,resid) < self.init_mse_board):                     self.init_mse_board /= 1.5                     self.add_to_max_depth += 1                     self.learning_rate /= 1.1                     # print ('Alert!', t, self.add_to_max_depth)                          if self.base_tree == 'Bagging':                 tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth,                                          min_size = self.min_size)                 resid = -resid                              if self.base_tree == 'Tree':                 tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size)                              if self.base_tree == 'XGBoost':                 tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size)                 resid = -resid                              tree.fit(X, resid)             b = tree.predict(X).reshape([X.shape[0]])             # print (b.shape)             self.trees_.append(tree)             prediction += self.learning_rate * b             temp_resid = resid          return self          def predict(self, X):                  # сначала прогноз – это просто вектор из средних значений ответов на обучении         pred = np.ones([X.shape[0]]) * np.mean(self.y)         # добавляем прогнозы деревьев         for t in range(self.n_estimators):             pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]])                      return pred

5. Результаты

По традиции, сравним результаты:

data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target)  import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn  er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging')) er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost')) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2))  %matplotlib inline data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost',  'XGBooBag']) plt.grid() plt.show()

Картинка будет следующая:

Самая низкая ошибка у XGBoost, но у XGBooBag ошибка более скученная, что определённо лучше: алгоритм более устойчив. На этом всё. Очень надеюсь, что материал, изложенный в двух статьях, был полезен, и вы смогли узнать для себя что-то новое. Особую благодарность выражаю Дмитрию за всестороннюю обратную связь и исходники, Антону — за советы, Владимиру — за сложные задания по учебе.

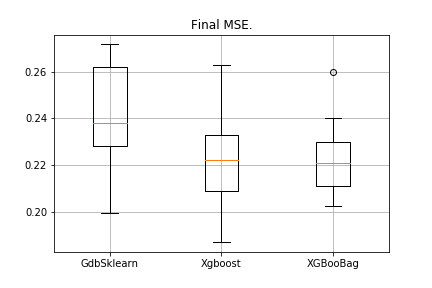
Всем успехов!