Линейные модели. Алгоритмы работы

Сверху мы видим метод работы линейной модели. Однако всё по порядку.

Произошла неприятная вещь - я не нашёл подходящего набора для данных, чтобы продемонстрировать все особенности "сегодняшних" алгоритмов :(. Потому сделаем уклон на теорию.

Линейная модель

Линейные модели - множество моделей, которые широко используют сегодня, а также являются объектом изучения больше сотни лет. Для прогнозирования используют линейную функцию(linear function) данных признаков.
Примечание. Все важные термины будут переведены на английский и обязательны к запоминанию.

Формула

Линейные модели используют такую формулу:

y = w[0] * x[0] + w[1] * x[1] + .... w[p] * x[p] + b

где x[0 .. p] - входные признаки(здесь их у нас p + 1); w[0 .. p] - линейные коэффициенты, которые модель получает при обучении; b - сдвиг(offset), который также вычисляется при обучении. Очень похоже на уравнение прямой, которое выглядит так:

y = k * x + b

Немного преобразуем его, исходя из объекта нашего исследования и получим:

y = w[0]* x[0] + b

Тут w[0] действительно является коэффициентом(тангенсом угла наклона), а b - сдвигом, оттуда и такие названия.

Альтернативные названия:

w[i] - регрессионный коэффициент (coefficients).

b - константа(intercept)

Виды моделей

Линейных моделей есть множество, и всё отличие заключается в способе расчёта коэффициентов и сдвига.

Обычная линейная регрессия

Линейная регрессия использует метод наименьших квадратов(ordinary least squares, OLS). Этот метод заключается в нахождении таких w и b, чтобы минимизировать среднюю квадратичную ошибку(mean squared error) между теми ответами, которые предсказывает наша модель и фактическими ответами из обучающей выборки.

Чтобы построить обычную модель линейной регрессии необходимо написать:

Чтобы узнать коэффициенты для каждого признака, воспользуемся полем LinearRegression.coef_, который возвращает массив NumPy со всеми коэффициентами. Для нахождения сдвига воспользуемся полем LinearRegression.intercept_ (всегда является числом с плавающей точкой).

Чтобы узнать правильность предсказаний модели, сделаем следующее

Отлично. Однако часто при работе с линейной регрессией мы можем получить недообучение (плохой результат что на тестовой, что на обучающей выборках) или переобучение(несоответствие результатов на обучающей и тестовых выборках). Для контролирования сложности модели и её результатов используют модификацию линейной регрессии - гребневую регрессию.

Гребневая регрессия

Метод работы этого алгоритма почти тот же, что и у "линейки", однако есть некоторые ограничения. Вся суть заключается в вычислении коэффициентов. Они выбираются не только со стороны их успешного предсказания результата, а и "сжимаются" до нуля. Что это даёт? С помощью этого уменьшается влияние определённых признаков на результат(например, в "линейке" у одного признака мог быть коэффициент 1500, а у другого 0.1, что делает первый признак "важнее" второго). Такое явление называется регуляризацией(regularization). Это даёт крепкую защиту от переобучения. Регуляризация, которая используется в гребневой регрессии называется L2-регуляризация.

Чтобы использовать гребневую регрессию, используем такой фрагмент кода:

Для нахождения коэффициентов и сдвига делаем то же самое, что и с линейной регрессией.

Именно "гребёнка" помогает найти нечто среднее между простотой модели и качеством её работы. У этого "нечто среднего" даже есть свой коэффициент - alpha. Этот параметр можно указать при инициализации класса Ridge.

Как оно работает? При увеличении alpha коэффициенты больше сжимаются к нулю, что может дать упадок правильности на обучающем наборе, однако дать прирост результативности на тестовой выборке. Однако не стоит этим баловаться постоянно, поскольку выбор alpha зависит только от конкретного датасета.

Лассо

Интересное название, не правда ли? Это третья разновидность линейной регрессии, которая отличается от "гребёнки" только тем, что тут коэффициенты могут равняться нулю! То есть значения некоторых признаков просто не используют.

Чтобы использовать лассо, нам нужен следующий фрагмент кода:

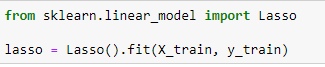
Чтобы узнать кол-во признаков, которые используются, необходимо выполнить следующее:

У него также есть параметр alpha, и отвечает он за ту же самую функцию.

Линейная классификация

Линейная классификация очень похожа на регрессию, за несколькими исключениями. Формула:

y = w[0] * x[0] + w[1] * x[1] + .... w[p] * x[p] + b > 0

Как мы видим, мы сравниваем значение y для определённого набора признаков, а затем сравниваем его с нулем - если y > 0, то возвращаем класс A, иначе возвращаем класс B.

Для линейных моделей моделей граница принятия решений(decision boundary) является линейной функцией. Другими словами при бинарном поиске(выборе из двух классов - A и В) линия разделяет два класса линией, плоскостью или гиперплоскостью(в зависимости от кол-ва измерений).

Ну вот и всё! Как только найду подходящий набор данных, реализуем практическое применение этих алгоритмов.

Источник: m.vk.com

Комментарии: