Важные аспекты математики в науке о данных-«что» и «почему»

Введение

Математика является фундаментом для любой современной научной дисциплины. И ни для кого не секрет, что почти все методы современной науки о данных (включая машинное обучение) строятся на тех или иных математических вычислениях.

Порой, будучи специалистом по обработке и анализу данных (или даже junior-аналитиком ) необходимо знать базовую математику, чтобы правильно применять ее методы. Для других целей можно использовать API или уже готовый алгоритм.

Но, в то же время, владение хорошими знаниями по математике, на которой строится ваш алгоритм для создания рекомендации по использованию продукта, никогда не навредит. Это даст вам преимущество перед вашими конкурентами и поможет вам сохранить уверенность в своих знаниях. Всегда полезно знать, что находится под капотом, а не просто сидеть за рулем, ничего не зная о машине.

Конечно, вам понадобятся и другие знания, навыки программирования, немного деловой хватки, уникальное аналитическое мышление и любознательность, касающиеся данных, которые так необходимы для ведущего специалисте по обработке и анализу данных. В данной статье я попытался собрать самые важные математические понятия, чтобы помочь вам в этом начинании.

Об особой важности для «новичков»

Знание основ математики особенно необходимо профессионалам, которые хотят перейти в эту область из другой специализации (разработка аппаратного обеспечения, торговля, химическая промышленность, медицина и здравоохранение, бизнес менеджмент, и т.д.).

И хотя они могут посчитать, что работали с таблицами, числовыми расчетами и прогнозами достаточно долго, в науке о данных требования к необходимым математическим навыкам значительно отличается от их текущей работы.

Как и почему требования отличаются—это НАУКА, а не ДАННЫЕ

Представьте веб-разработчика (или бизнес-аналитика). Он(а) ежедневно работает с большим объемом данных и информации, но не сталкивается со скрупулезным моделированием этих данных. Часто, для таких специалистов создают строгие временные рамки, и акцент делается на «использовании данных здесь и сейчас и затем работать дальше», а не на детальном научном исследовании этих данных. Нравится вам или нет, наука о данных всегда остается наукой (а не данными). Исходя из этого, определенные инструменты и методы являются незаменимыми. Многие из них являются критериями хорошего научного процесса:

• Моделирование процесса (физического или информативного) путем исследования основных динамик.
• Построение гипотез.
• Тщательная оценка качества источника данных.
• Количественная оценка неопределенности, касающейся данных и прогнозов.
• Развитие навыка идентификации скрытой характеристики в потоке информации.
• Четкое понимание ограниченности модели.
• (Иногда) понимание математического доказательства и всей абстрактной логики, на которой строится доказательство.

Такой вид обучения (большая его часть) развивает способность мыслить не одними числами, а абстрактными математическими категориями (а также их свойствами и взаимосвязями). Он преподносится как часть стандартной образовательной программы четырехлетнего обучения в университете. Не нужно иметь красный диплом ведущего университета, чтобы получить знания о такой математике. Но, к сожалению, мы не пользуемся этой доступностью ?

И я говорю не о дифференциальном исчислении, которое проходят на первом курсе университета, а о чем-то более простом… Как цифра 2…

Скажем, вы, отдохнувший и готовый заняться сложными графиками, садитесь утром за свой рабочий стол. Вдруг на почту вам приходит сообщение от начальника (или от друга с математическим складом ума) со следующим заданием: «Докажи, что квадратный корень из 2 не является рациональным числом. У тебя 2 минуты».

Что… Что еще за рациональное число?

Поняли, о чем я?

Хватит разговоров—покажи мне план, как добиться успеха

И вот в чем проблема. Нет никакого универсального плана. Наука о данных, по сути, не привязана к какой-то конкретной предметной области. Она занимается такими разнообразными явлениями, как диагностика рака и анализ социального поведения в рамках одного проекта. Это дает возможность пересекать огромное множество n-мерных математических объектов, статических распределений, целевых функций оптимизации и…

Остановись. Пожалуйста.

Что все это вообще такое? Я серьезно.

Итак, вот мои отобранные предложения по темам, которые пригодятся нам для того, чтобы стоять на вершине игры в науке о данных (почти…).

Функции, переменные, уравнения, графики:

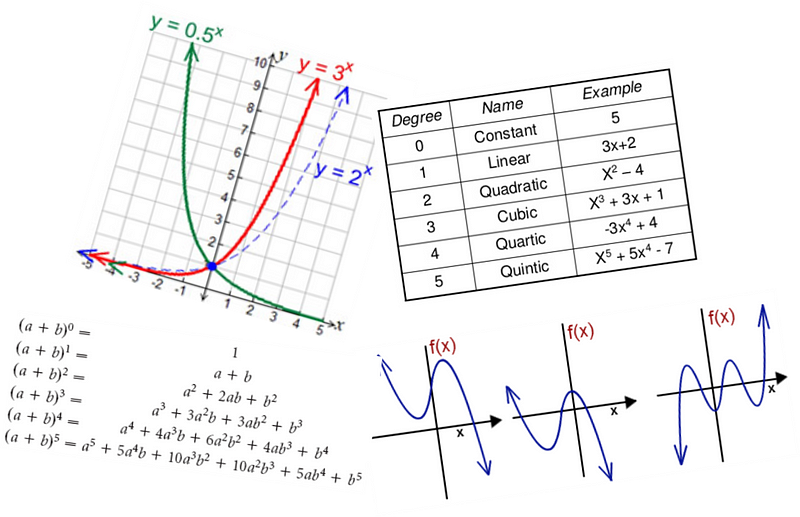
Что: начнем таких основных вещей, как линейные уравнения, и закончим на биноме Ньютона и его свойствах.

• Логарифм, экспоненциальные, полиномиальные функции, рациональные числа.
• Основы геометрии и базовые теоремы, тригонометрические тождества.
• Вещественные и комплексные числа, их основные свойства.
• Ряды, суммы и неравенства.
• Построение графиков, системы прямоугольной и полярной координат, конические сечения.

Где их можно использовать: если хотите понять, как быстро найти что-либо в базе данных с миллионом отсортированных элементов, то вам понадобится концепция бинарного поиска. Чтобы понять динамику, необходимо для начала разобраться с логарифмами и рекуррентными уравнениями. Или, если хотите проанализировать временные ряды, используйте такие концепции, как периодические функции и экспоненциальный закон.

Статистика:

Что: о чем нужно знать, чтобы развиваться как специалист по обработке данных. Важность четкого понимания основных концепций статистики и вероятности нельзя переоценить в дискуссиях о науке о данных. Многие практики в этой области называют классическое машинное обучение (не нейронную сеть) не чем иным, как статистическим обучением. Данная тема обширна и бесконечна, и поэтому сфокусированное планирование крайне важно для того, чтобы охватить максимальное количество основных понятий.

• Сводные данные и описательная статистика, среднее значение, дисперсия, ковариация, корреляция.
• Основы теории вероятности: основные идеи, ожидание, исчисление вероятностей, теорема Байеса, условная вероятность.
• Функции распределения вероятностей—равномерное, нормальное, биномиальное, хи-квадрат, распределение Стьюдента, центральная предельная теорема.
• Сэмплирование, измерение, ошибка, генератор случайных чисел.
• Проверка гипотез, А/В-тестирование, доверительный интервал, Р-значение.
• ANOVA, t-критерий.
• Линейная регрессия, регуляризация.

Где их можно использовать: во время собеседований. Поверьте. Будучи перспективным специалистом по обработке данных, освоив все вышеперечисленные концепции, вам удастся быстро произвести хорошее впечатление на будущего работодателя. Во время работы вам часто придется сталкиваться с необходимостью использовать те или иные концепции.

Линейная алгебра:

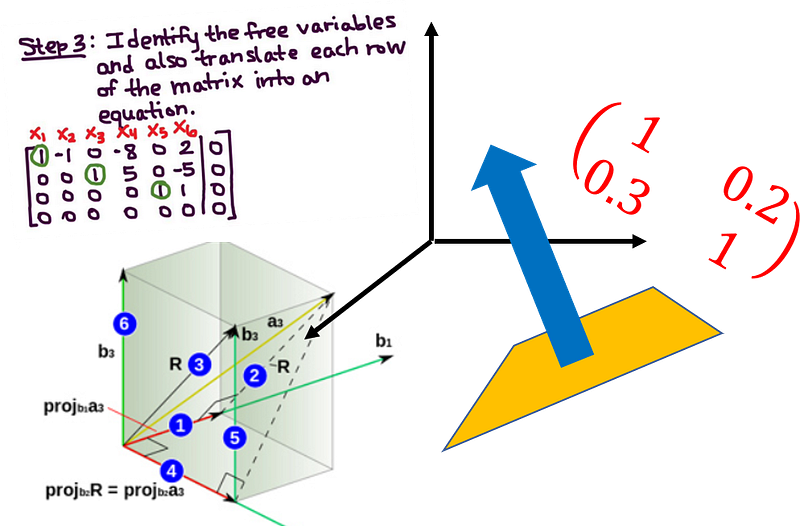
Что: рекомендации друзей в Facebook, рекомендации песен в Spotify, придание фотографии эффекта в стиле Сальвадора Дали с использованием переноса обучения глубоких нейронных сетей. Что у них всех общего? Везде применяются матрицы и алгебра матриц. Алгебра матриц является важным аспектом математики, которая помогает понять, как большая часть алгоритмов машинного обучения функционирует в потоке данных. Ниже приведены наиболее важные темы для изучения:

• Основные свойства матрицы и векторов—скалярное произведение, линейное преобразование, транспонирование, сопряжение, ранг, определитель.
• Внутреннее и внешнее произведение, правило умножения матриц и различные алгоритмы, обратная матрица.
• Пространственные матрицы—квадратная, единичная, треугольная, разреженная, плотная, симметричная, Эрмитова, антиэрмитова и унитарная матрицы, единичный вектор.
• Понятие матричного разложения/LU-разложение, метод Гаусса/Гаусса-Жордана, решение систем линейных алгебраических уравнений вида Ax=b.
• Векторное пространство, базис, оболочка, ортогональность, метод линейных наименьших квадратов.
• Собственное значение матрицы, собственный вектор, диагонализация, сингулярное разложение (SVD).

Где их можно использовать: если вы применяете метод главных компонент (PCA) для снижения размерности, то скорее всего вы используете сингулярное разложение для более компактной размерности данных с меньшим количеством параметров. Все алгоритмы нейронной сети используют методы линейной алгебры для представления и обработки сетевых структур и обучающих операций.

Математический анализ

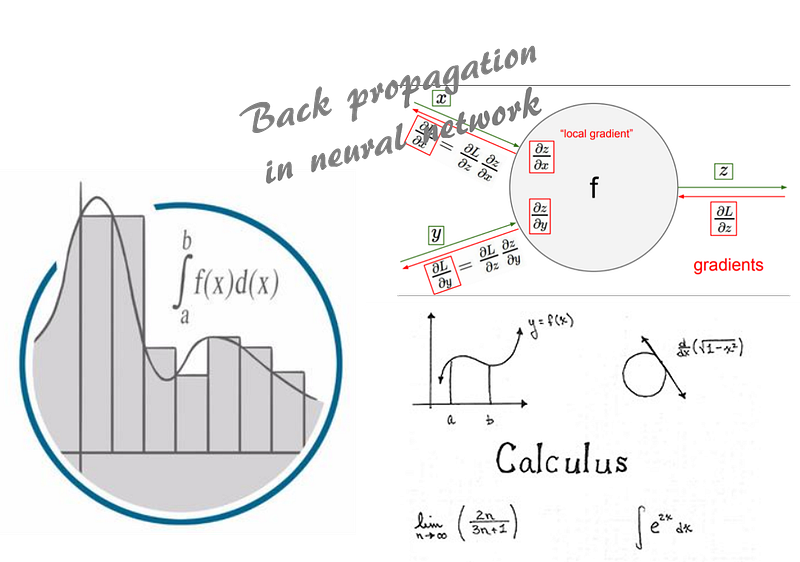
Что: независимо от того, нравился он вам в университете или нет, с математическим анализом мы сталкиваемся во многих аспектах науки о данных и машинного обучения. Он скрывается за простым, на первый взгляд, аналитическим решением обычной задачи с наименьшим значением квадратичной функции в линейной регрессии. Также он внедрен в каждый метод обратного распространения ошибки, создаваемой нейронной сетью для обучения. Знания о математическом анализе окажутся очень ценными для вашей работы. Ниже приведены темы для изучения:

• Функция одной переменной, предел, непрерывность и дифференцируемость.
• Формула конечных приращений, раскрытие неопределенностей, теорема Лопиталя.
• Максимум и минимум.
• Правила произведения и дифференцирования сложной функции.
• Ряд Тейлора, суммирование бесконечного ряда/понятие интегрирования.
• Основная теорема и формула конечных приращений интегрального исчисления, вычисление определенного и несобственного интегралов.
• Бета- и Гамма-функции.
• Функции множества переменных, предел, непрерывность и частные производные.
• Основы обыкновенных дифференциальных уравнений и дифференциальных уравнений в частных производных (не самые сложные).

Где их можно использовать: вы наверняка задумывались, как все-таки используется алгоритм логистической регрессии. Для нахождения минимума функции потерь очень часто применяется метод градиентного спуска. Чтобы понять, как это работает, необходимо использовать концепции математического анализа: градиент, производные, пределы, дифференцирование сложной функции.

Дискретная математика

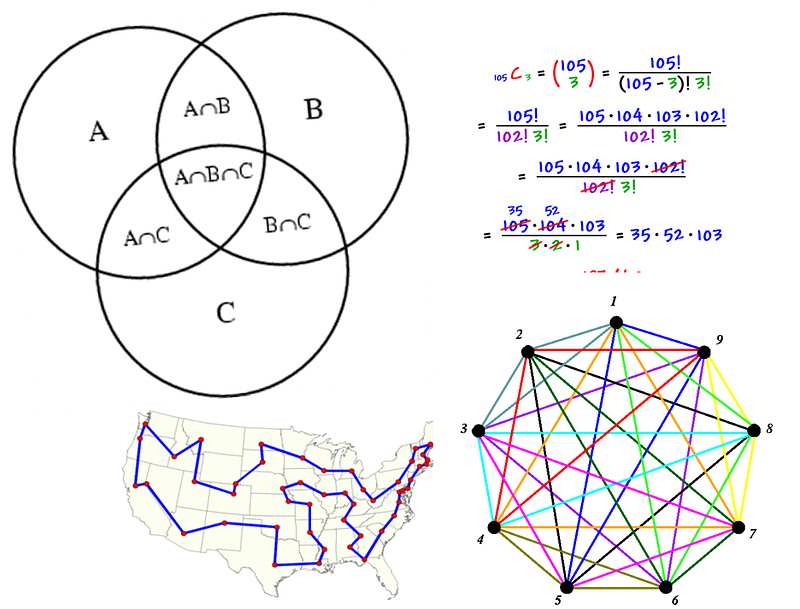
Что: дискретную математику редко затрагивают, говоря о такой теме, как «математика в науке о данных». Но, тем не менее, современная наука о данных строится с помощью вычислительных систем, в которых дискретная математика является ключевым элементом. Курсы по дискретной математике помогут освоить важные концепции для ежедневного использования алгоритмов и структур данных при работе над аналитическими проектами. Ниже приведены некоторые темы для изучения:

• Множество, подмножество, булеан.
• Считающие функции, комбинаторика, счетность.
• Основные методы доказательства—индукция, доказательство от противного.
• Основы индуктивной, дедуктивной и пропозиционной логики.
• Основные структуры данных—стеки, очередь, графы, массивы, хеш-таблицы, деревья.
• Инварианты графов: компоненты связности, степень вершины, теорема Форда—Фалкерсона, раскраска графов.
• Рекуррентные формулы (уравнения, соотношения).
• Рост функции, нотация «O» большое.

Где их можно использовать: инварианты графов и быстрые алгоритмы необходимо знать при анализе любых социальных сетей. При любом алгоритме нужно понять временную и пространственную сложность, используя нотацию «О» большое. Это необходимо, например, при определении того, как растет продолжительность работы и необходимый размер с увеличением количества входных данных.

Оптимизация, темы исследования операций

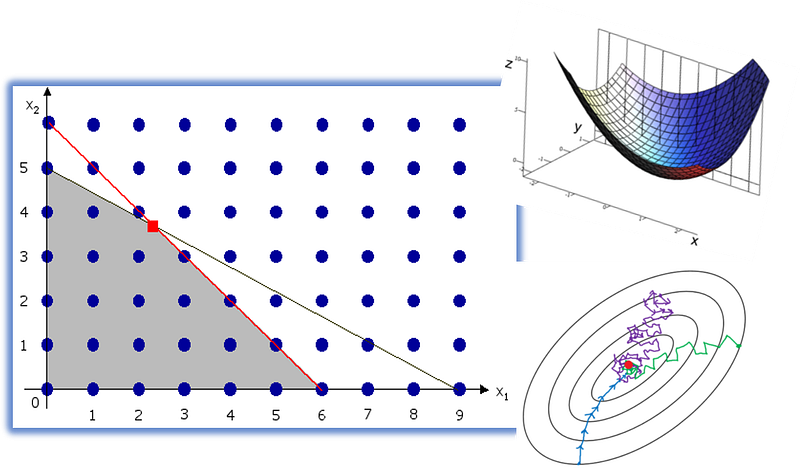
Что: все эти темы мало чем отличается от традиционного дискурса прикладной математики, так как они в основном являются важными и наиболее используемыми в специализированных областях изучения: в теоретической информатике, теории управления, исследовании операций. Но общее понимание данных эффективных методов может оказаться чрезвычайно полезно в сфере машинного обучения. Практически каждый алгоритм/метод машинного обучения направлен на минимизацию своего рода ошибки оценки с учетом различных ограничений. Это и является задачей оптимизации. Темы для изучения:

• Основы оптимизации—как сформулировать задачу.
• Максимум, минимум, выпуклая функция, глобальное решение.
• Линейное программирование, симплекс-метод.
• Целочисленное программирование.
• Программирование в ограничениях, задача о рюкзаке.
• Рандомизированные методы оптимизации—поиск восхождением к вершине, алгоритм имитации отжига, генетический алгоритм.

Где их можно использовать: простые задачи линейной регрессии, в отличие от логистической, с использованием функции потерь наименьших квадратов часто имеют точное аналитическое решение. Чтобы понять причину, нужно знать о таком понятии, как выпуклость в оптимизации. Это также пояснит то, почему нам должно быть достаточно «приблизительных» решений во многих задачах машинного обучения. Оптимизация является мощным инструментом, который стоит изучить подробно.

И некоторые советы

Не пугайтесь и не теряйтесь. Да, много. Но все вышеперечисленное необходимо изучить и понять, особенно если вы не сталкиваетесь с данными вещами регулярно. В интернете можно найти отличные обучающие сайты и видео. Выделив немного времени и сил, вы можете составить свой список таких сайтов в соответствии с вашими личными потребностями.

И будьте уверены, повторив данные темы (многие из которых вы проходили в университете) и изучив новые концепции, вы настолько улучшите свои навыки, что начнете слышать скрытую мелодию в вашей ежедневной работе над обработкой данных или в проектах машинного обучения. И это будет большим шагом к тому, чтобы стать специалистом по обработке данных…

Перевод статьи Tirthajyoti Sarkar: Essential Math for Data Science—‘Why’ and ‘How’