Дискретное преобразование Фурье (ДПФ)

Введение

Дискретное преобразование Фурье (ДПФ) — один из распространенных инструментов спектрального анализа сигналов, широко применяемый в самых разных отраслях науки и техники. При этом разработано множество быстрых алгоритмов для высокой вычислительной эффективности ДПФ.

В данном разделе будет уделено особое внимание переходу от непрерывного интеграла Фурье к дискретно-временному преобразованию Фурье (ДВПФ) и, далее, к дискретному преобразованию Фурье. Понимание данного перехода позволит лучше понять свойства ДПФ и сущность цифрового спектрального анализа в целом.

Пара непрерывного преобразования Фурье (интеграл Фурье) имеет вид:

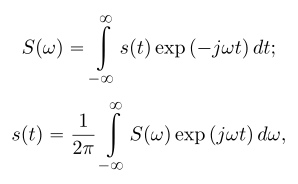
где S(w) — спектр сигнала s(t) (в общем случае и сигнал и спектр — комплексные).

Выражения для прямого ДПФ и обратного дискретного преобразования Фурье (ОДПФ) имеют вид:

ДПФ ставит в соответствие N отсчетам сигнала s(n), n = 0…N-1, N отсчетов комплексного спектра Sd(k), k = 0…N-1 . Здесь и далее в данном разделе переменная n индексирует временные отсчеты сигнала, а переменная k индексирует спектральные отсчеты ДПФ.

Как в непрерывном, так и в дискретном случаях в выражениях для обратного преобразования имеется нормировочный коэффициент. В случае интеграла Фурье это 1 / 2?, в случае ОДПФ – 1/N.

Нормировочный коэффициент необходим для корректного масштабирования сигнала из частотной области во временную. Нормировочный коэффициент уменьшает амплитуду сигнала на выходе обратного преобразования, для того чтобы она совпадала с амплитудой исходного сигнала. Если последовательно рассчитать прямое преобразование Фурье некоторого сигнала, а после взять обратное преобразование Фурье, то результат обратного преобразования должен полностью совпадать с исходным сигналом.

Дискретизация сигнала по времени. Дискретно-временное преобразование Фурье.

Рассмотрим дискретный сигнал Sd(t) как результат умножения непрерывного сигнала s(t) на решетчатую функцию:

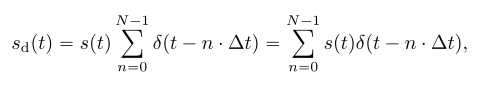
где ?(t) – дельта-функция:

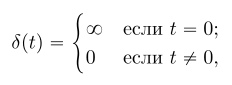
?t – интервал дискретизации. Графически процесс дискретизации можно представить, как это показано на рисунке 1.

Вычислим преобразование Фурье дискретного сигнала Sd(t), для этого подставим выражение (3) в выражение для преобразования Фурье (1):

Поменяем местами операции суммирования и интегрирования и используем фильтрующее свойство дельта-функции:

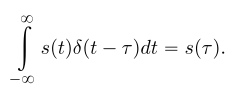
Тогда выражение (5) с учетом (6) принимает вид:

Таким образом, мы избавились от интегрирования в бесконечных пределах, заменив его конечным суммированием комплексных экспонент.

Комплексные экспоненты exp[- j?n?t] в выражении (7) являются периодическими функциями с периодом:

где Fs = 1/?t — частота дискретизации сигнала (Гц).

Необходимо отметить, что n = 0 исключено из выражения (8), так как при n = 0 комплексная экспонента равна единице. Максимальный период повторения спектра Sd(?) будет при n = 1, в этом случае он равен

Таким образом, спектр Sd(?) дискретного сигнала Sd(t), есть 2?Fs — периодическая функция циклической частоты ?, определенная как (7). Если мы введем нормировку частоты дискретизации Fs = 1 Гц, то (7) переходит к выражению дискретно-временного преобразования Фурье (ДВПФ):

ДВПФ использует только индексы отсчетов входного сигнала S(n) при частоте дискретизации Fs = 1 Гц. В результате ДВПФ мы получим 2? периодическую функцию Sd(?н) нормированной циклической частоты ?н = ? / Fs.

Поскольку спектр дискретного сигнала — периодическая функция, то можно рассматривать только один период повторения спектра Sd(?) при ? = [0; 2?Fs] рад/с или Sd(f) при f = [0; Fs] Гц.

Повторение сигнала во времени. Дискретное преобразование Фурье

Для программной реализации алгоритмов цифровой обработки требуются как дискретные отсчеты сигнала, так и дискретные отсчеты спектра. Известно что дискретным, или, как еще говорят, линейчатым спектром, обладают периодические сигналы. При этом дискретный спектр получается путем разложения в ряд Фурье периодического сигнала. Значит, чтобы получить дискретный спектр, надо сделать исходный дискретный сигнал периодическим путем повторения данного сигнала во времени бесконечное количество раз с некоторым периодом . Тогда спектр периодического сигнала будет содержать дискретные гармоники, кратные ?? = 2? / T рад/c.

Графически процесс повторения сигнала во времени представлен на рисунке 2.

Черным показан исходный сигнал, красным — его повторения через некоторый период .

Повторять сигнал можно с различным периодом T, однако необходимо, чтобы период повторения был больше или равен длительности сигнала T > N * ?t, чтобы сигнал и его периодические повторения не перекрывались во времени. При этом минимальный период повторения сигнала Tmin, при котором сигнал и его повторения не накладываются друг на друга, равен

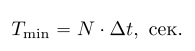
Повторение сигнала с минимальным периодом Tmin = N * ?t показано на рисунке 3.

При повторении сигнала с минимальным периодом Tmin получим линейчатый спектр сигнала, состоящий из гармоник, кратных:

Таким образом, мы можем продискретизировать спектр Sd(?) дискретного сигнала s(n) на одном периоде повторения 2?Fs с шагом ?? = 2? / (N * ?t) и получим

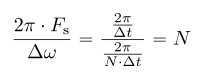
отсчетов спектра.

Учтем вышесказанное в выражении (7):

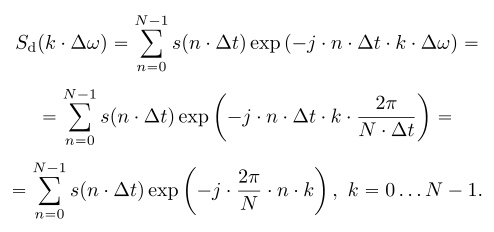
Если опустить в выражении (13) шаг дискретизации по времени ?t и по частоте ??, то получим окончательное выражение для ДПФ:

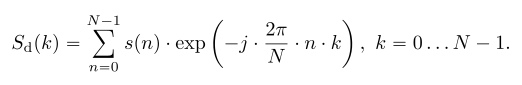
ДПФ ставит в соответствие N отсчетам дискретного сигнала s(n), N отсчетов дискретного спектра Sd(k), при этом предполагается, что и сигнал и спектр являются периодическими и анализируются на одном периоде повторения.

Обратное дискретное преобразование Фурье

Список литературы

[1] Сергиенко А.Б. Цифровая обработка сигналов Питер, 2002.

[2] Оппенгейм А., Шафер Р. Цифровая обработка сигналов Техносфера, 2006.

[3] Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов Радио и связь, 1985.

[4] Bracewell R.N. The Fourier Transform and its Applications. McGraw Hill, Singapor, 2000.

[5] Oppenheim Alan V. and Schafer Ronald W. Discrete-Time Signal Processing Second Edition. Prentice-Hall, New Jersey, 1999.

[6] Robert J. Marks II The Joy of Fourier: Analysis, Sampling Theory, Systems, Multidimensions, Stochastic Processes, Random Variables, Signal Recovery, Pocs, Time Scales, & Applications. Baylor University, 2006.

[7] Nussbaumer Henri J. Fast Fourier Transform and Convolution Algorithms. Second Corrected and Updated Edition. Springer-Verlag, 1982.

Источник: m.vk.com

Комментарии: