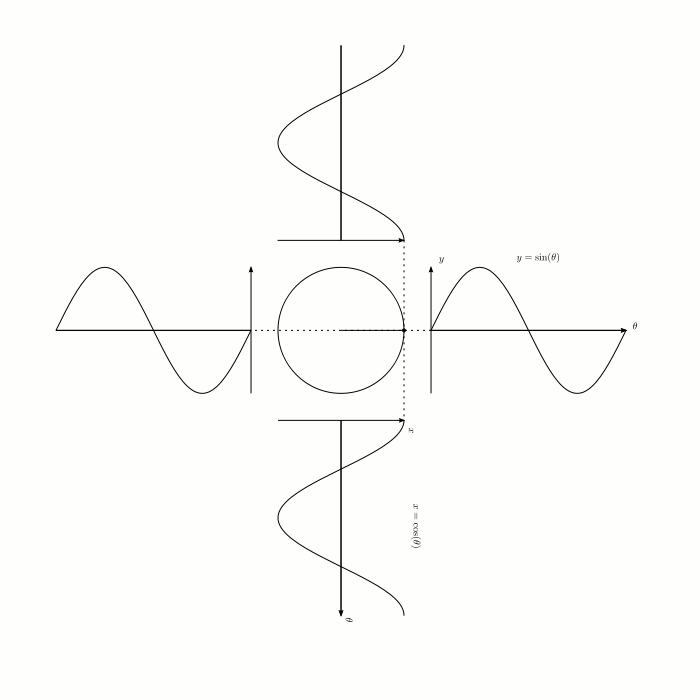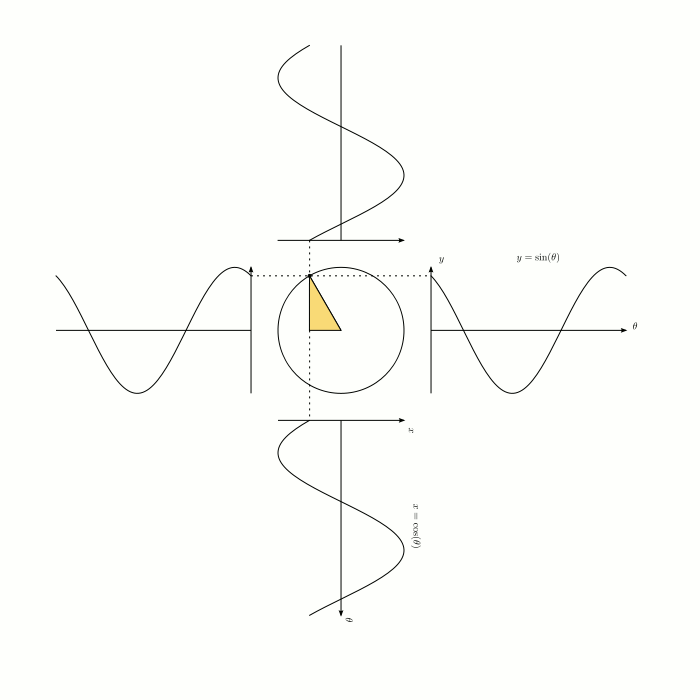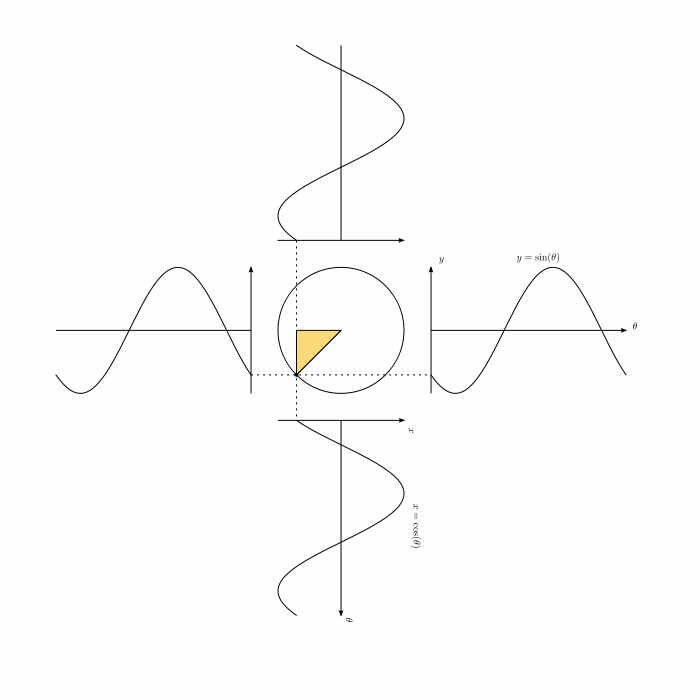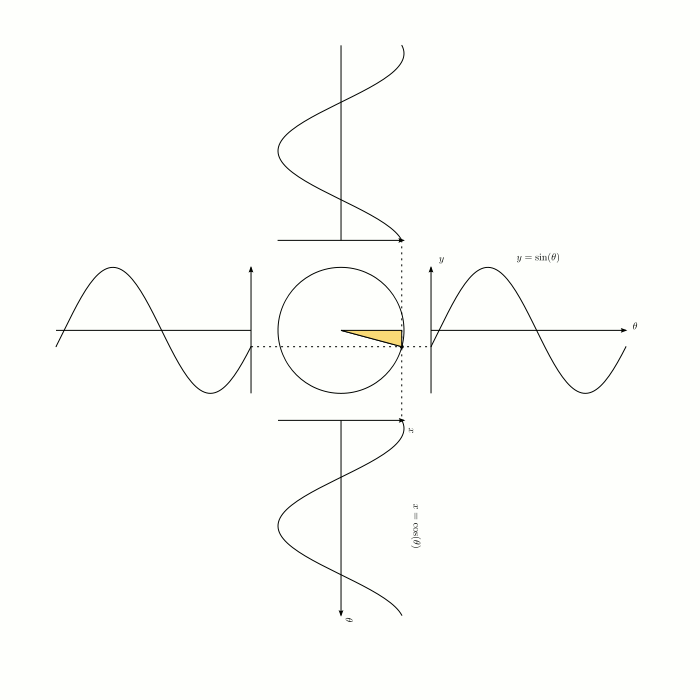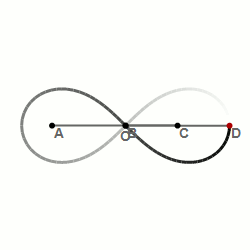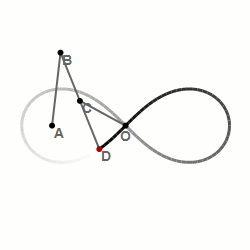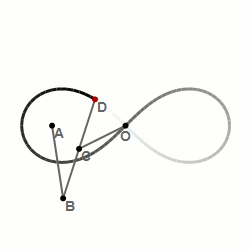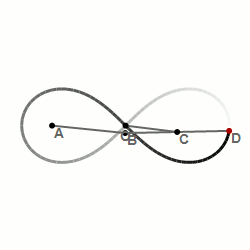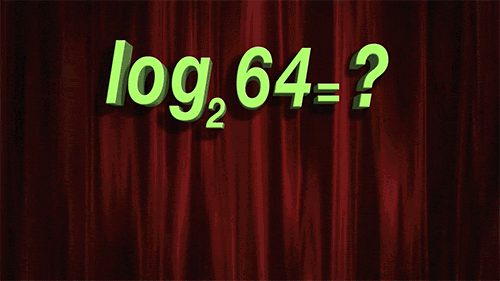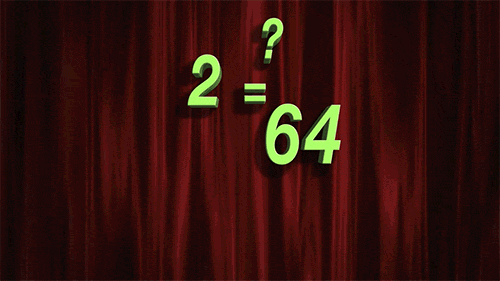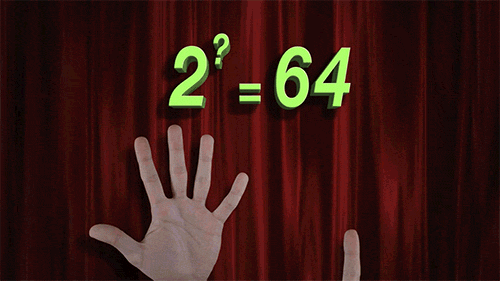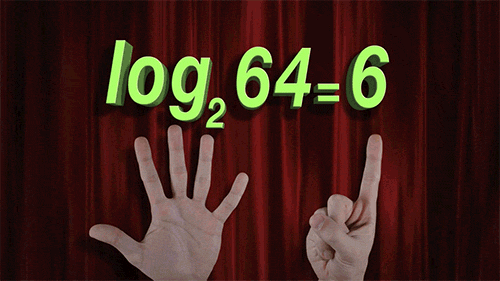20 гифок, которые объяснят математику простым языком (20 гиф)

Лист бумаги, сложенный методом миура-ори:

Все углы треугольника могут быть прямыми, если треугольник начерчен на сфере:

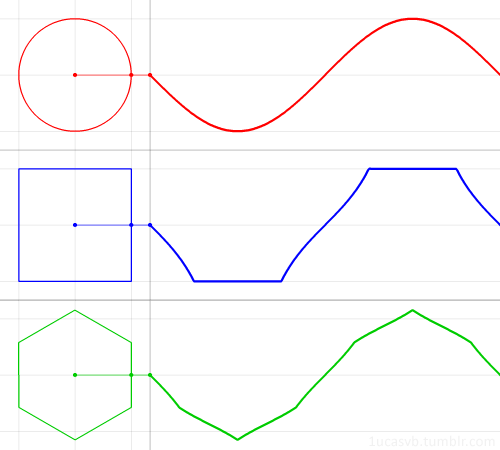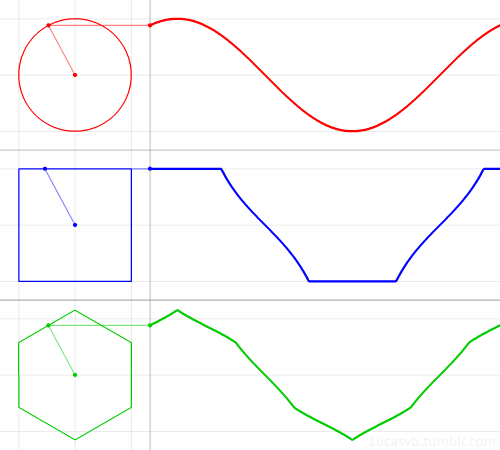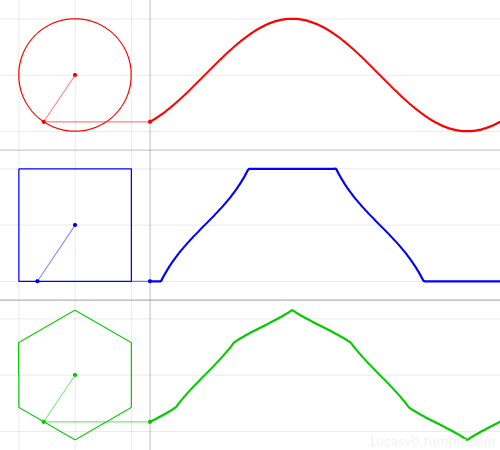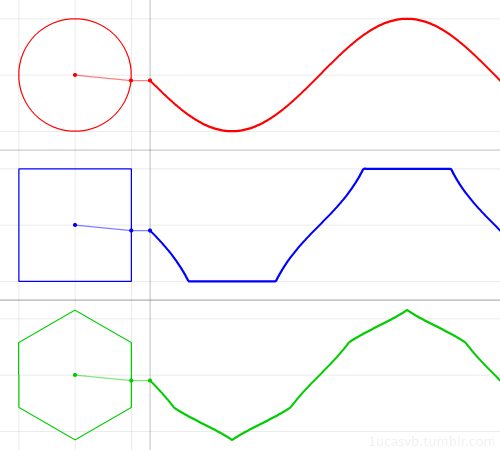
Визуализация синуса и косинуса:

Треугольник Рёло — простейшая после круга фигура постоянной ширины. Если к треугольнику Рёло провести пару параллельных опорных прямых, то независимо от выбранного направления расстояние между ними будет постоянным:

Построение треугольника Серпинского с помощью рекурсии:

А так математики шутят:

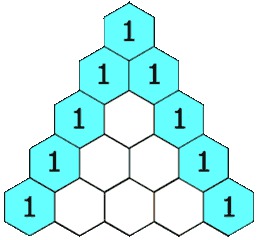
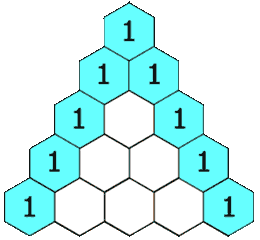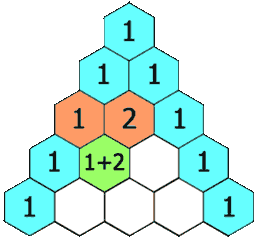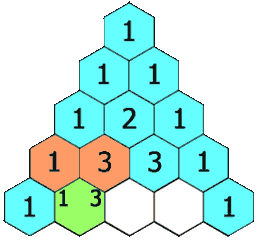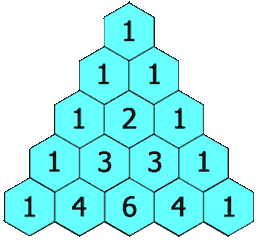
Как работает треугольник Паскаля (на вершине и по бокам — единицы, каждое число равно сумме чисел, расположенных над ним):

Если вывернуть тор наизнанку, получится еще один:

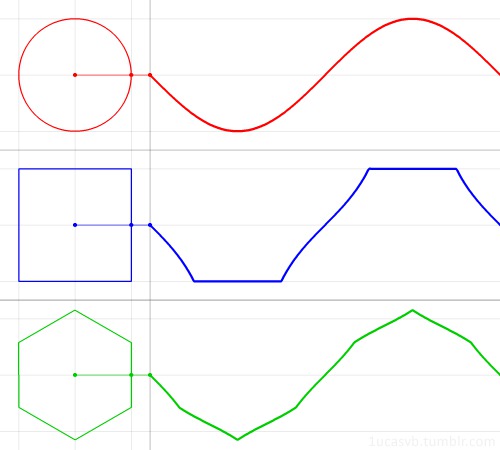
Немного построений графиков:

Решето Эратосфена — алгоритм нахождения простых чисел до числа n:

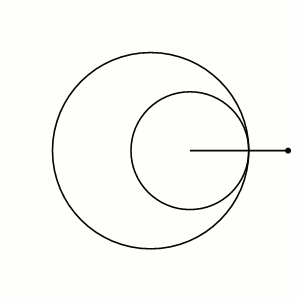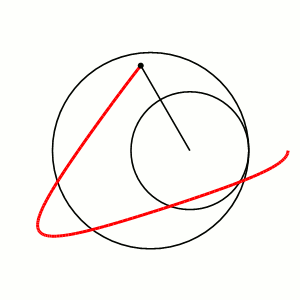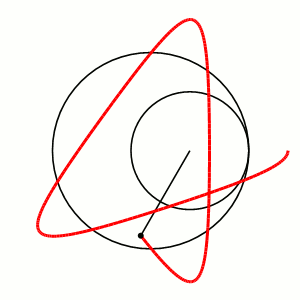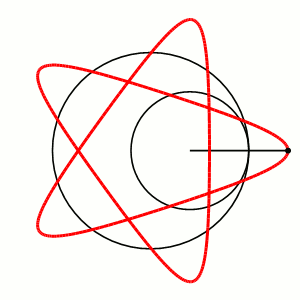
Построение гипотрохоиды:

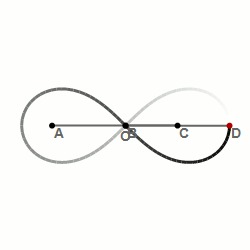
Шарнирный метод построения лемнискаты Бернулли — алгебраической кривой, похожей на символ бесконечности:

Так выглядит фрактал:

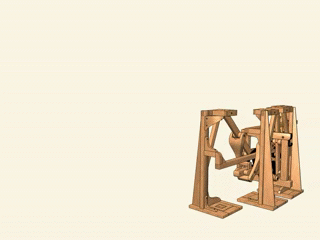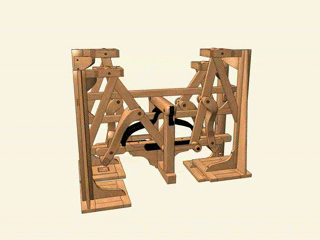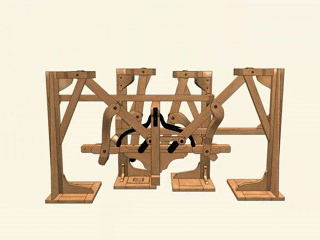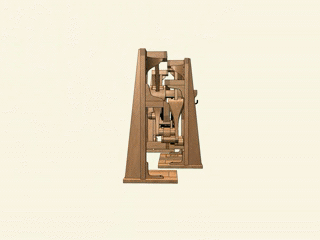
Стопходящая машина Чебышева. Да-да, прямо как робот из «Звездных войн»:

Как площадь круга соотносится с треугольником:

Любите математику!

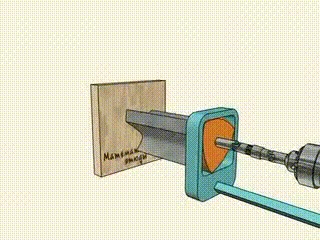
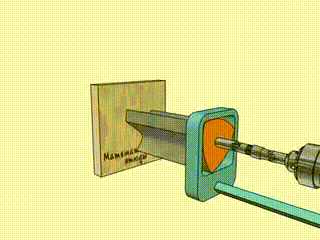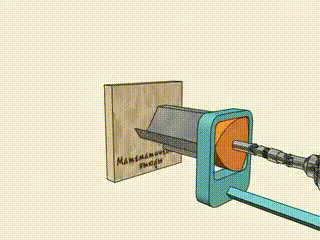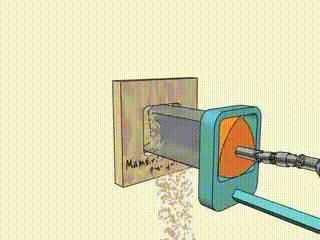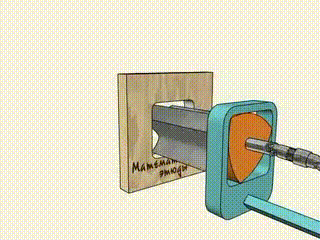
И с его помощью можно сверлить квадратные отверстия:

Теорема Пифагора:

Как понять логарифмы:

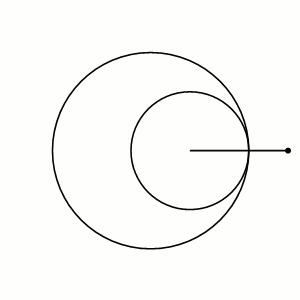
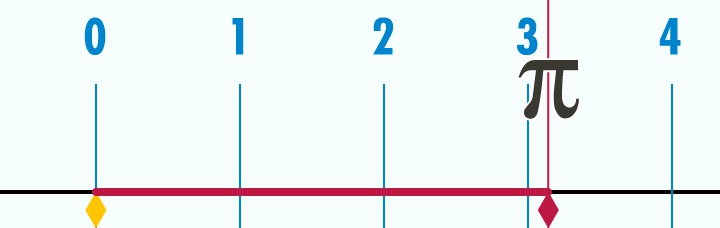
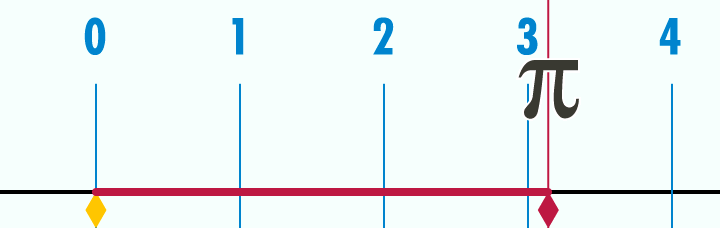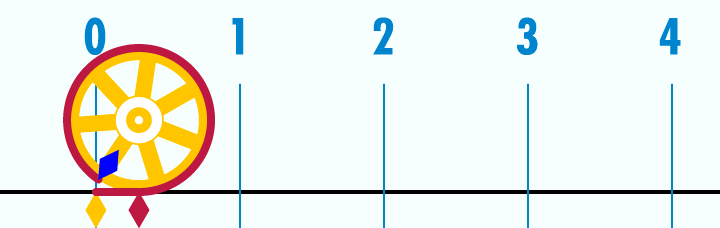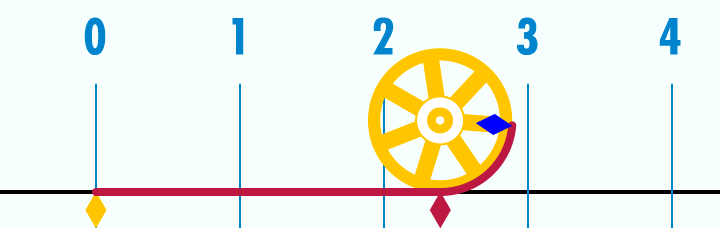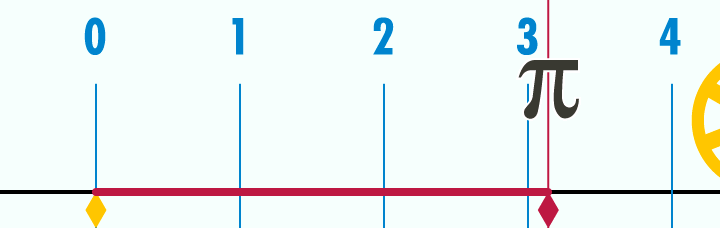
Как на самом деле выглядит число Пи: