Когда не нужно использовать алгоритмы из STL

Я боролся с соблазном назвать статью как-то типа «Ужасающая неэффективность алгоритмов STL» — ну, знаете, просто ради тренировки в мастерстве создания кричащих заголовков. Но всё же решил оставаться в рамках приличий — лучше получить от читателей комментарии по содержанию статьи, чем негодование по поводу её громкого названия.

В этом месте я предположу, что вы немного знаете С++ и STL, а также заботитесь об используемых в вашем коде алгоритмах, их сложности и соответствия поставленным задачам.

Алгоритмы

Одним из хорошо известных советов, которые вы можете услышать от современного сообщества разработчиков на С++, будет не придумывать велосипеды, а использовать алгоритмы из стандартной библиотеки. Это хороший совет. Данные алгоритмы безопасны, быстры, проверены годами. Я тоже часто даю совет применять их.

Каждый раз, когда вам хочется написать очередной for — следует сначала вспомнить, нет ли в STL (или в boost) чего-то, что уже решает эту задачу в одну строку. Если есть — чаще лучше использовать это. Нам, однако, и в этом случае следует понимать, что за алгоритм лежит за вызовом стандартной функции, каковы его характеристики и ограничения.

Обычно, если наша проблема в точности совпадает с описанием алгоритма из STL, будет хорошей идеей взять и применить его «в лоб». Беда только в том, что данные не всегда хранятся в том виде, в котором их хочет получить реализованный в стандартной библиотеке алгоритм. Тогда у нас может возникнуть идея сначала преобразовать данные, а потом всё же применить тот же алгоритм. Ну, знаете, как в том анекдоте про математика «Затушить огонь из чайника. Задача сведена к предыдущей».

Пересечение множеств

Представьте, что мы пытаемся написать инструмент для программистов на С++, который будет находить в коде все лямбды с захватом всех переменных по умолчанию ([=] и [&]) и выводить советы по преобразованию их в лямбды с конкретным списком захватываемых переменных. Как-то вот так:

std::partition(begin(elements), end(elements),     [=] (auto element) {    //^~~ - захватывать всё подряд не хорошо, замените на [threshold]         return element > threshold;     });

По ходу разбора файла с кодом, нам придётся где-то хранить коллекцию переменных в текущей и окружающей области видимости, а при обнаружении лямбды с захватом всех переменных сравнить эти две коллекции и дать совет по её преобразованию.

Одно множество с переменными родительской области видимости, и ещё одно с переменными внутри лямбды. Для формирования совета разработчику нужно всего лишь найти их пересечение. И это тот случай, когда описание алгоритма из STL просто идеально подходит к задаче: std::set_intersectionпринимает два множества и возвращает их пересечение. Алгоритм прекрасен в своей простоте. Он принимает две отсортированные коллекции и проходит по ним параллельно:

• Если текущий элемент в первой коллекции идентичен текущему элементу во второй — добавляем его в результат и переходим к следующим элементам в обеих коллекциях
• Если текущий элемент в первой коллекции меньше текущего элемента во второй коллекции — переходим к следующему элементу в первой коллекции
• Если текущий элемент в первой коллекции больше текущего элемента во второй коллекции — переходим к следующему элементу во второй коллекции

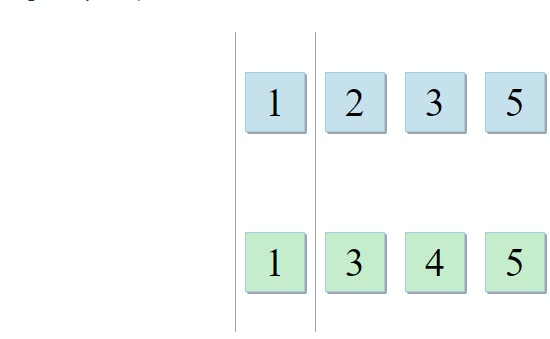
C каждым шагом алгоритма мы движемся по первой, второй или обеим коллекциями, а значит сложность данного алгоритма будет линейной — О(m + n), где n и m — это размеры коллекций.

Просто и эффективно. Но это лишь пока входные коллекции отсортированы.

Сортировка

Проблема в том, что в общем случае коллекции не отсортированы. В нашем конкретном случае удобно хранить переменные в какой-нибудь стеко-подобной структуре данных, добавляя переменные на очередной уровень стека при входе во вложенную область видимости и удаляя их из стека при выходе из данной области видимости.

Это означает, что переменные не будут отсортированы по имени и мы не можем напрямую использовать std::set_intersection на их коллекциях. Поскольку std::set_intersection требует на входе именно отсортированные коллекции, может возникнуть мысль (и я часто видел такой подход в реальных проектах) отсортировать коллекции перед вызовом библиотечной функции.

Сортировка в данном случае убьёт всю идею использования стека для хранения переменных соответственно их областям видимости, но всё же это возможно:

template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_1(InputIt1 first1, InputIt1 last1,                               InputIt2 first2, InputIt2 last2,                               OutputIt dest) {     std::sort(first1, last1);     std::sort(first2, last2);     return std::set_intersection(first1, last1, first2, last2, dest); }

Какова сложность полученного алгоритма? Что-то типа O(n log n + m log m + n + m) — квазилинейная сложность.

Меньше сортировок

Можем ли мы не использовать сортировку? Можем, почему бы и нет. Просто будем искать каждый элемент из первой коллекции во второй, линейным поиском. Получим сложность O(n * m). И этот подход я также видел в реальных проектах достаточно часто.

Вместо вариантов «сортировать всё» и «не сортировать ничего» мы можем попробовать найди Дзен и пойти третьим путём — сортировать лишь одну из коллекций. Если одна из коллекций будет отсортирована, а вторая нет, то мы сможем перебирать элементы неотсортированной коллекции по одному и искать их в отсортированной бинарным поиском.

Сложность этого алгоритма будет составлять O(n log n) для сортировки первой коллекции и O (m log n) для поиска и проверки. В сумме получим сложность O((n + m) log n).

Если мы решим отсортировать другую из коллекций, то получим сложность O((n + m) log m). Как вы понимаете, логичным здесь будет сортировать коллекцию меньшего размера для получения итоговой сложности О((m + n) log (min(m, n))

Реализация будет выглядеть вот так:

template <typename InputIt1, typename InputIt2, typename OutputIt> auto unordered_intersection_2(InputIt1 first1, InputIt1 last1,                               InputIt2 first2, InputIt2 last2,                               OutputIt dest) {     const auto size1 = std::distance(first1, last1);     const auto size2 = std::distance(first2, last2);      if (size1 > size2) {         unordered_intersection_2(first2, last2, first1, last1, dest);         return;     }      std::sort(first1, last1);      return std::copy_if(first2, last2, dest,         [&] (auto&& value) {             return std::binary_search(first1, last1, FWD(value));         }); }

В нашем примере с лямбда-функциями и захватом переменных, коллекцией, которую мы будем сортировать, обычно будет коллекция переменных, используемых в коде лямбда-функции, поскольку их, скорее всего, будет меньше, чем переменных в окружающей лямбду области видимости.

Хеширование

И последней рассматриваемой в данной статье опцией будет использование хеширования для меньшей коллекции вместо её сортировки. Это даст нам возможность искать в ней за О(1), хотя само построение хеша, конечно, займёт некоторое время (от O(n) до O(n*n), что может стать проблемой):

template <typename InputIt1, typename InputIt2, typename OutputIt> void unordered_intersection_3(InputIt1 first1, InputIt1 last1,                               InputIt2 first2, InputIt2 last2,                               OutputIt dest) {     const auto size1 = std::distance(first1, last1);     const auto size2 = std::distance(first2, last2);      if (size1 > size2) {         unordered_intersection_3(first2, last2, first1, last1, dest);         return;     }      std::unordered_set<int> test_set(first1, last1);      return std::copy_if(first2, last2, dest,         [&] (auto&& value) {             return test_set.count(FWD(value));         }); }

Подход с хешированием будет абсолютным победителем в случае, когда нашей задачей является последовательно сравнить некоторое небольшое множество А с набором других (больших) множеств B?, B?, В…. В этом случае нам нужно построить хеш для А лишь один раз, а использовать его мгновенный поиск можно будет для сравнения с элементами всех рассматриваемых множеств В.

Тест производительности

Всегда полезно подтвердить теорию практикой (особенно в случаях подобно последнему, когда не ясно, окупятся ли первоначальные затраты на хеширование приростом производительности на поиске).
В моих тестах первый вариант (с сортировкой обеих коллекций) всегда показывал худшие результаты. Сортировка одной лишь меньшей коллекции работала чуть лучше на коллекциях одинаковых размеров, но не слишком. Но и второй и третий алгоритм показали очень существенный прирост производительности (примерно в 6 раз) в случаях, когда одна из коллекций была в 1000 раз больше другой.

Источник: m.vk.com

Комментарии: