Простое введение в АЛУ для нейронных сетей: пояснение, физический смысл и реализация

Недавно исследователи из Google DeepMind, в том числе известный учёный в сфере искусственного интеллекта, автор книги "Разбираемся в глубоком обучении", Эндрю Траск, опубликовали впечатляющую статью, описывающую модель нейронной сети для экстраполяции значений простых и сложных численных функций с большой степенью точности. В этой статье я объясню архитектуру НАЛУ (нейронных арифметико-логических устройств, NALU), их компоненты и существенные отличия от традиционных нейронных сетей. Главная цель этого поста — просто и интуитивно понятно объяснить NALU (и реализацию, и идею) для учёных, программистов и студентов, мало знакомых с нейронными сетями и глубоким обучением.

Примечание от автора: я так же очень рекомендую прочитать оригинальную статью для более детального изучения темы.

Когда нейронные сети ошибаются?

Изображение взято из этой статьи

В теории, нейронные сети должны хорошо аппроксимировать функции. Они почти всегда способны выявлять значимые соответствия между входными данными (факторами или фичами) и выходными (ярлыками или таргетами). Именно поэтому они используются во многих сферах, от распознавания объектов и их классификации до перевода речи в текст и реализации игровых алгоритмов, способных обыграть чемпионов мира. Уже создано много различных моделей: конволюционные и рекуррентные нейронные сети, автокодировщики, и т.д. Успехи в создании новых моделей нейронных сетей и глубоком обучении — сама по себе большая тема для изучения.

Однако, по словам авторов статьи, нейронные сети не всегда справляются с задачами, кажущимися очевидными людям, и даже пчёлам! Например, это устный счёт или операции с числами, а также умение выявлять зависимость из соотношений. В статье было показано, что стандартные модели нейронных сетей не справляются даже с тождественным отображением (функцией, переводящей аргумент в себя, $$) — самым очевидным числовым соотношением. На рисунке ниже изображена MSE различных моделей нейронных сетей при обучении на значениях данной функции.

На рисунке изображена средняя квадратическая ошибка для стандартных нейронных сетей, использующих одинаковую архитектуру и различные (нелинейные) функции активации во внутренних слоях

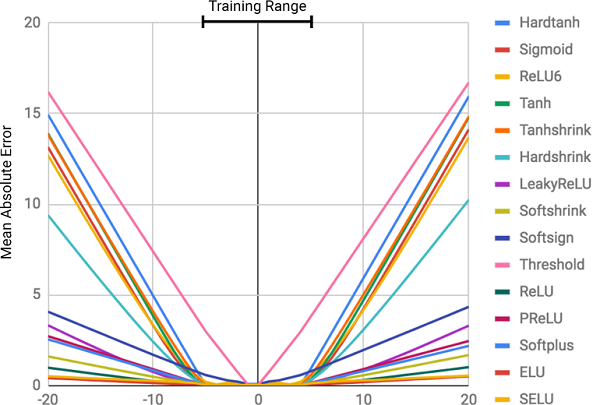
Почему нейронные сети ошибаются?

Как видно из рисунка, основная причина промахов заключается в нелинейности функций активации на внутренних слоях нейронной сети. Такой подход отлично работает для определения нелинейных связей между входными данными и ответами, но ужасно ошибается при выходе за пределы данных, на которых сеть училась. Таким образом, нейронные сети отлично справляются с запоминанием числовой зависимости из тренировочных данных, но не умеют её экстраполировать.

Это похоже на зубрёжку ответа или темы перед экзаменом, но без понимания сути изучаемого предмета. Легко сдать тест, если вопросы похожи на домашние задания, но если проверяется именно понимание предмета, а не способность запоминать, нас ждёт неудача.

Этого не было в программе курса!

Степень ошибки напрямую связана с уровнем нелинейности выбранной функции активации. Из предыдущей диаграммы отчётливо видно, что нелинейные функции с жёсткими ограничениями, как, например, сигмоида (Sigmoid) или гиперболический тангенс (Tanh), справляются с задачей обобщения зависимости гораздо хуже функций с мягкими ограничениями, например, усечённого линейного преобразования (ELU, PReLU).

Решение: Нейронный Аккумулятор (NAC)

Нейронный аккумулятор (NAC) лежит в основе модели NALU. Это простая, но эффективная часть нейронной сети, справляющаяся со сложением и вычитанием — необходимыми умениями для эффективного вычисления линейных связей.

NAC — это специальный линейный слой нейронной сети, на веса которого наложено простое условие: они могут принимать всего 3 значения: 1, 0 или -1. Такие ограничения не позволяют аккумулятору изменять диапазон значений входных данных, и он остаётся постоянным на всех слоях сети, независимо от их количества и связей. Таким образом, выход является линейной комбинацией значений входного вектора, что легко может представлять собой операции сложения и вычитания.

Мысли вслух: для лучшего понимания данного утверждения давайте рассмотрим пример построения слоёв нейронной сети, выполняющих линейные арифметические операции над входными данными.

На рисунке поясняется, как слои нейронной сети без добавления константы и с возможными значениями весов -1, 0, или 1, могут выполнять линейную экстраполяцию

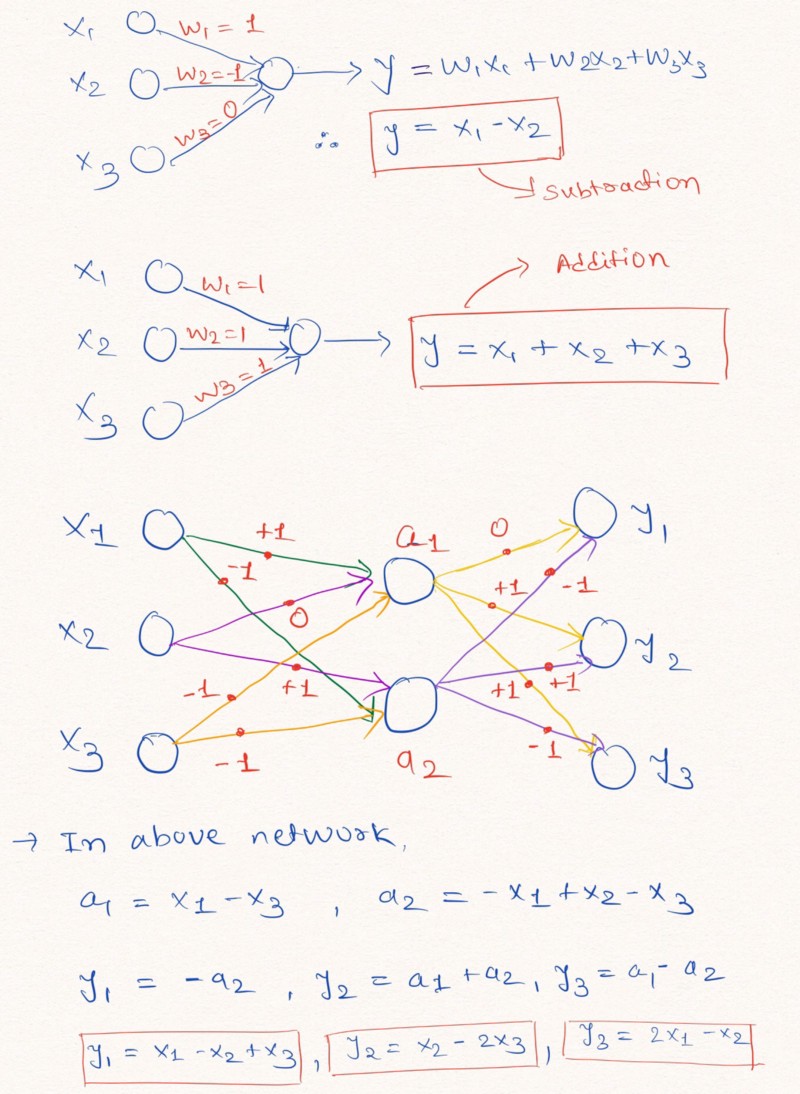
Как показано сверху на изображении слоёв, нейронная сеть может научиться экстраполировать значения таких простейших арифметических функций, как сложение и вычитание ($$ и $$) с помощью ограничений весов возможными значениями 1, 0 и -1.

Примечание: слой NAC в данном случае не содержит свободного члена (константы) и не применяет нелинейных преобразований к данным.

Так как стандартные нейронные сети не справляются с решением задачи при подобных ограничениях, авторы статьи предлагают очень полезную формулу для вычисления таких параметров через классические (неограниченные) параметры $$ и $$. Данные веса, подобно всем параметрам нейронных сетей, могут быть инициализированы случайным образом и могут быть подобраны в процессе обучения сети. Формула для вычисления вектора $$ через $$ и $$ выглядит так:

$$

В формуле используется поэлементное произведение матриц

Использование данной формулы гарантирует ограниченность области значений W отрезком [-1, 1], что уже ближе к набору -1, 0, 1. Также функции из данного уравнения являются дифференцируемыми по весовым параметрам. Таким образом, нашему слою NAC будет проще обучаться значениям $$ с помощью градиентного спуска и обратному распространению ошибки. Ниже приведена диаграмма с архитектурой слоя NAC

Архитектура нейронного аккумулятора для обучения на элементарных (линейных) арифметических функциях

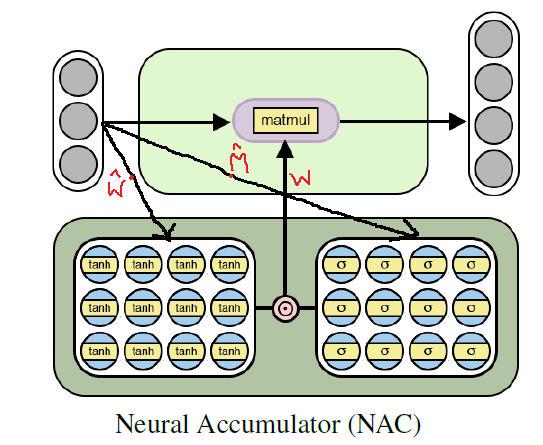
Реализация NAC на Python с использованием Tensorflow

Как мы уже понимаем, NAC является довольно простой нейронной сетью с небольшими особенностями. Ниже представлена реализация одного слоя NAC на Python с использованием библиотек Tensoflow и NumPy.

Python код

import numpy as np import tensorflow as tf  # Определение нейронного аккумулятора (NAC) для сложения/вычитания # -> Помогает при подборе операций сложения/вычитания def nac_simple_single_layer(x_in, out_units):    '''    Принимаемые параметры:        x_in -> Входной тензор X        out_units -> размер выходного вектора     Возвращаемые значения:       y_out -> Результирующий тензор заданной размерности       W -> Матрица весов для слоя    '''    # Определяем количество строк во входных данных    in_features = x_in.shape[1]     # инициализируем W_hat и M_hat    W_hat = tf.get_variable(shape=[in_shape, out_units],                            initializer=tf.initializers.random_uniform(minval=-2, maxval=2),                            trainable=True,                            name='W_hat')     M_hat = tf.get_variable(shape=[in_shape, out_units],                            initializer=tf.initializers.random_uniform(minval=-2, maxval=2),                            trainable=True,                            name='M_hat')     # Считаем W по формуле    W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat)     y_out = tf.matmul(x_in, W)     return y_out, W 

В приведённом коде $$ и $$ инициализируются с помощью равномерного распределения, но вы можете использовать любой рекомендованный способ генерации начального приближения для этих параметров. Вы можете ознакомиться с полной версией кода в моём GitHub репозитории (ссылка дублируется в конце поста).

Двигаемся дальше: от сложения и вычитания к NAC для сложных арифметических выражений

Хотя описанная выше модель несложной нейронной сети справляется с простейшими операциями вроде сложения и вычитания, нам необходимо уметь обучаться и на множестве значений более сложных функций, таких как умножение, деление и возведение в степень.

Ниже вы видите изменённую архитектуру NAC, которая способна подбирать более сложные арифметические операции через логарифмирование и взятие экспоненты внутри модели. Обратите внимание на отличия данной реализации NAC от уже рассмотренной выше.

Архитектура NAC для более сложных арифметических операций

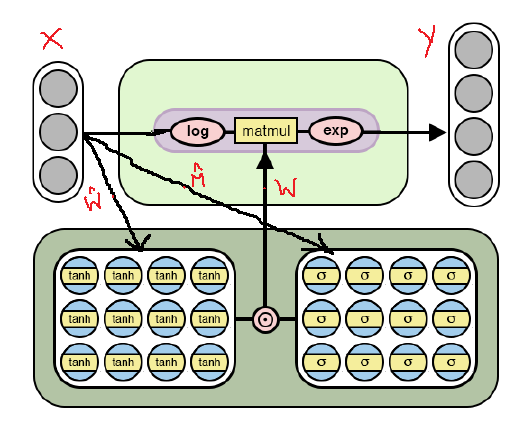
Как видно из рисунка, мы логарифмируем входные данные до умножения на матрицу весов, а затем вычисляем экспоненту получившегося результата. Формула для расчётов имеет следующий вид:

$$

Формула выходных данных для второй версии NAC. $$ здесь это очень маленькое число для предотвращения ситуаций вида log(0) во время обучения.

Таким образом, для обеих моделей NAC принцип действия, в том числе вычисление матрицы весов с ограничениями $$ через $$ и $$, не меняется. Единственным различием является применение логарифмических операций над входом и выходом во втором случае.

Вторая версия NAC на Python с использованием Tensorflow

Код, как и архитектура, почти не изменится, исключая указанные доработки вычислений тензора выходных значений.

Python код

# Определение нейронного аккумулятора (NAC) с добавлением логарифмических операций # -> Помогает при подборе более сложных операций, таких как умножение, деление и возведение в степень def nac_complex_single_layer(x_in, out_units, epsilon=0.000001):    '''    :param x_in: Входной тензор X    :param out_units: размер выходного вектора    :param epsilon: маленькое положительное число (нужно, чтобы избежать ситуации log(0) при подсчёте результата)    :return m: Результирующий тензор заданной размерности    :return W: Матрица весов для слоя    '''     in_features = x_in.shape[1]     W_hat = tf.get_variable(shape=[in_shape, out_units],                            initializer=tf.initializers.random_uniform(minval=-2, maxval=2),                            trainable=True,                            name="W_hat")     M_hat = tf.get_variable(shape=[in_shape, out_units],                            initializer=tf.initializers.random_uniform(minval=-2, maxval=2),                            trainable=True,                            name="M_hat")     # Считаем W по формуле    W = tf.nn.tanh(W_hat) * tf.nn.sigmoid(M_hat)     # Логарифмируем входные данные для обучения на сложных арифметических операциях    x_modified = tf.log(tf.abs(x_in) + epsilon)     m = tf.exp(tf.matmul(x_modified, W))     return m, W 

Очередное напоминание, что полную версию кода мы можете найти в моём GitHub репозитории (ссылка дублируется в конце поста).

Собираем всё вместе: Нейронное Арифметическо-Логическое Устройство (NALU)

Как многие уже догадались, мы можем обучаться практически на любых арифметических операциях, комбинируя две рассмотренных выше модели. Это и есть основная идея NALU, включающего в себя взвешенную комбинацию элементарного и сложного NAC, контролируемую через обучающий сигнал. Таким образом, NAC являются кирпичиками для сборки NALU, и, если вы разобрались в их устройстве, построить NALU будет просто. Если же у вас остались вопросы, попробуйте ещё раз прочитать пояснения к обеим моделям NAC. Ниже приведена диаграмма с архитектурой NALU.

Диаграмма архитектуры NALU с пояснениями

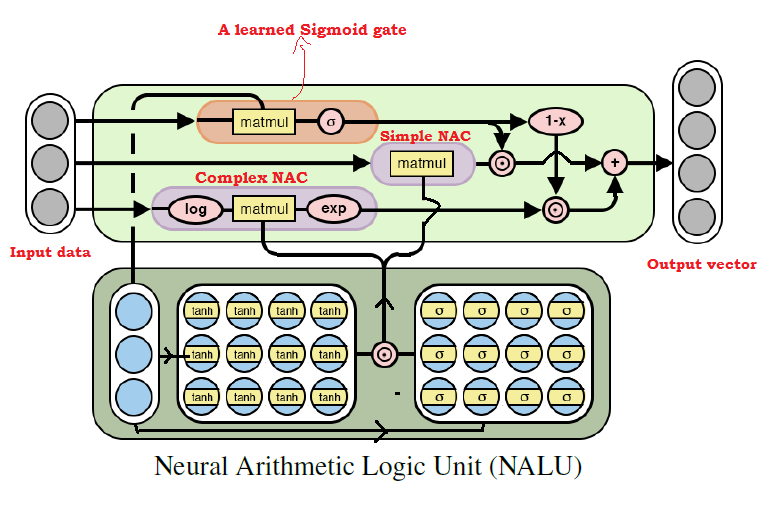
Как видно из рисунка выше, оба блока NAC (фиолетовые блоки) внутри NALU интерполируются (комбинируются) через сигмоиду обучающего сигнала (оранжевый блок). Это позволяет (де)активировать выходные данные любого из них в зависимости от арифметической функции, значения которой мы пытаемся подобрать.

Как было сказано выше, элементарный блок NAC представляет собой аккумулирующую функцию, что позволяет выполнять NALU элементарные линейные операции (сложение и вычитание), в то время как сложный блок NAC отвечает за умножение, деление и возведение в степень. Выходные данные в NALU могут быть представлены в виде формулы:

Псевдокод

Simple NAC : a = W X Complex NAC: m = exp(W log(|X| + e))  Где W = tanh(W_hat) * sigmoid(M_hat)  # Здесь G - стандартная матрица параметров для обучения Контролирующий сигнал: g = sigmoid(G X) # И, наконец, выходные данные NALU # Здесь * является поэлементным умножением для матриц NALU: y = g * a + (1 - g) * m 

Из формулы NALU выше можно сделать вывод, что при значении $$ нейронная сеть будет подбирать только значения для сложных арифметических операций, но не для элементарных, и наоборот в случае $$. Таким образом, в целом NALU способно обучаться на любой арифметической операции, состоящей из сложения, вычитания, умножения, деления и возведения в степень и успешно экстраполировать полученный результат за пределы интервалов значений исходных данных.

Реализация NALU на Python с использованием Tensorflow

В реализации NALU мы будем использовать элементарный и сложный NAC, уже определённые в коде ранее.

Python код

def nalu(x_in, out_units, epsilon=0.000001, get_weights=False):    '''    :param x_in: Входной тензор X    :param out_units: размер выходного вектора    :param epsilon: маленькое положительное число (нужно, чтобы избежать ситуации log(0) при подсчёте результата)    :param get_weights: При значении True возвращает подсчитанные матрицы весов модели     :return y_out: Результирующий тензор заданной размерности    :return G: Кoнтролирующая матрица весов    :return W_simple: матрица весов для NAC1 (элементарный NAC)    :return W_complex: матрица весов для NAC2 (сложный NAC)    '''     in_features = x_in.shape[1]     # Получаем результат из элементарного NAC    a, W_simple = nac_simple_single_layer(x_in, out_units)     # Получаем результат из сложного NAC    m, W_complex = nac_complex_single_layer(x_in, out_units, epsilon=epsilon)     # Сигнал контролирующего слоя    G = tf.get_variable(shape=[in_shape, out_units],                        initializer=tf.random_normal_initializer(stddev=1.0),                        trainable=True,                        name="Gate_weights")     g = tf.nn.sigmoid(tf.matmul(x_in, G))     y_out = g * a + (1 - g) * m     if(get_weights):        return y_out, G, W_simple, W_complex    else:        return y_out 

Ещё раз отмечу, что в коде выше я снова инициализировал матрицу параметров $$ с помощью равномерного распределения, но вы можете использовать любой рекомендованный способ генерации начального приближения.

---

Итоги

Лично для меня идея NALU является серьёзным прорывом в сфере ИИ, особенно в нейронных сетях, и выглядит она многообещающе. Данный подход может открыть двери в те сферы применения, где стандартные нейронные сети не справлялись.

Авторы статьи рассказывают о различных экспериментах с использованием NALU: от подбора значений элементарных арифметических функций до подсчёта количества рукописных цифр в заданных сериях изображений MNIST, что позволяет нейронным сетям проверять компьютерные программы! Результаты выглядят потрясающими и доказывают, что NALU справляется с практически любыми задачами, связанными с числовым представлением, лучше стандартных моделей нейронных сетей. Я рекомендую читателям ознакомиться с результатами экспериментов, чтобы лучше понять, как и где идея NALU может быть полезна.

Тем не менее, нужно помнить, что ни NAC, ни NALU не являются идеальным решением для любой задачи. Они скорее представляют общую идею того, как можно создавать модели для конкретного класса арифметических операций.

---

Ниже приведена ссылка на мой GitHub репозиторий, где содержится полная реализация кода из статьи.
github.com/faizan2786/nalu_implementation Вы можете самостоятельно проверить работу моей модели на различных функциях, подбирая гиперпараметры для нейронной сети. Пожалуйста, задавайте вопросы и делитесь мыслями в комментариях под этим постом, и я сделаю всё возможное, чтобы вам ответить. PS (от автора): это мой первый когда-либо написанный пост, так что, если у вас есть любые советы, предложения и рекомендации на будущее (как технического плана, так и нетехнического), пожалуйста, напишите мне.

PPS (от переводчика): если у вас есть замечания к переводу или к тексту, пожалуйста, напишите мне личное сообщение. Особенно меня интересует формулировка для learned gate signal — не уверен, что смог точно перевести этот термин.