Почему логистическая (сигмоидная) регрессия является обобщенной линейной моделью, не являясь линейной на самом деле.

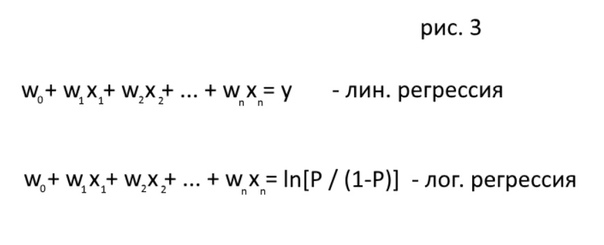
Сегодня будет краткое пояснялово, почему логистическая (сигмоидная) регрессия является обобщенной линейной моделью, не являясь линейной на самом деле.

Последний пикрелейтед – вывод функции потерь для логистической регрессии через функцию правдоподобия выборки, кому не лень заебаться.

Напомню, что самым тривиальным подходом к задаче классификации объектов на два класса является логистическая регрессия. Она ищет (например, градиентным спуском) такую гиперплоскость, что та делит объекты, максимизируя отступы между объектами одного класса и гиперплоскостью И В ТО ЖЕ ВРЕМЯ объектами другого класса и гиперплоскостью. Ну или минимизируя свою функцию потерь – очень уебищную из-за такого какича, как сигмоида (о ней ниже).

Внутри всего этого говна лежит простая сумма входных переменных Х с весами w0 + w1x1 + w2x2 + w3x3 + ... + wnxn, где х – это входная перменная, w - её вес. Простой многочлен первой степени. В итоге это обычная линейная модель? Нет, тебя наебали.

Дело в том, что в логистической регрессии нарушается главное предположение линейной регресии – линейная зависимость между наблюдаемыми (Х) и зависимой (у) переменными. Зависимая переменная в случае двуклассовой классификации – это бинарная переменная, 0 или 1. Рост Х не влечет за собой рост 1. Но вырастает же вероятность принадлежности к 1? Да, вырастает.

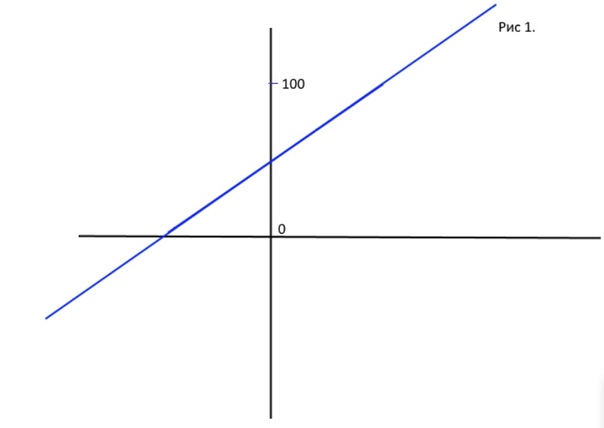
Так почему тогда не сделать просто линейную регрессию - взвешенную сумму, ответом которой будет число от 0 до 100, характеризующее процент принадлежности объекта к классу? Потому что модель будет обобщать поведение функции и в <0, и в >100, что не имеет смысла (рис 1). Ты не можешь гарантировать, что на вход не будут поданы такие переменные Х, что ответ не вылезет за 100.

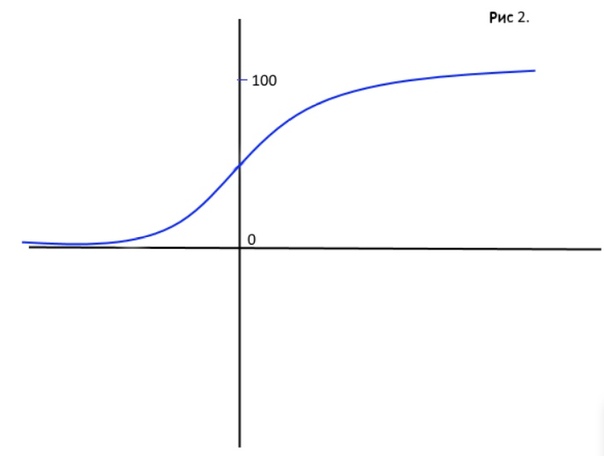
Поэтому главный какич логистической регрессии – это её сигмоида. Функция, которая сжимает твою взвешенную сумму (-?; +?) в отрезок вероятности P?[0; 1], и при принадлежности объекта к классу 1 на 50% та самая сумма переменных Х с весами будет равна 0 (рис 2.).

На практике же самое ощутимое отличие логистической регрессии от линейной регрессии – это её плохая интерпретируемость. Например, в линейной регрессии приращение одной переменной х на единицу изменяет ответ у на вес этой переменной – просто прибавляет или вычитает. А в логистической регрессии то же приращение вызывает изменение P / P - 1 в exp(w) раз (этот пердеж вылазит из всё той же сигмоидной ебучки) (рис 3).

Резюмируя:

Взвешенная сумма входных переменных линейна к её, кхм блед, ответу, а именно логарифмическому коэффициенту ln(P / 1 - P) и нелинейна к самой зависимой переменной P – вероятности принадлежности классу. Ввиду нелинейности зависимости модель не является линейной.

Но при том, что эта модель не является линейной, она ТРЕБУЕТ ЛИНЕЙНОЙ РАЗДЕЛИМОСТИ ОБЪЕКТОВ. То есть через объекты должно быть возможно провести прямую (в случае двумерного пространства, или двух входных переменных). В этом большинство путается.

Ну а обобщенной линейной моделью логистическая регрессия является просто потому, что внутри функции связи Х-Y (сигмоиды) лежит линейная комбинация – взвешенная сумма входных переменных.

Комментарии: