AI, практический курс. Глубокое обучение для генерации музыки

Это последняя статья в серии обучающих статей для разработчиков в сфере искусственного интеллекта. В ней рассматриваются шаги по созданию модели глубокого обучения для генерации музыки, выбор подходящей модели и предварительная обработка данных, а также описываются процедуры задания, обучения, тестирования и модификации BachBot.

Генерация музыки — размышление над задачей

Первым этапом в решении множества задач с помощью средств искусственного интеллекта (ИИ) является сведение задачи к базовой проблеме, которая решается средствами ИИ. Одной из таких проблем является предсказание последовательности, которое используется в приложениях для перевода и обработки естественного языка. Нашу задачу по генерации музыки можно свести к проблеме предсказания последовательности, при этом предсказание будет выполняться для последовательности музыкальных нот.

Выбор модели

Существует несколько различных видов нейронных сетей, которые можно рассматривать в качестве модели: нейросети прямого распространения, рекуррентные нейросети и нейросети с долгой краткосрочной памятью.

Нейроны являются базовыми абстрактными элементами, которые объединяются для формирования нейронных сетей. По существу, нейрон представляет собой функцию, которая принимает на входе данные и выдает на выходе результат.

Нейрон

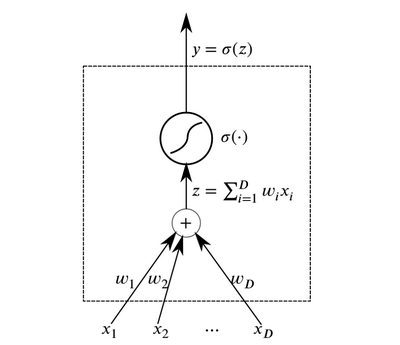
Слои из нейронов, принимающие на входе одинаковые данные и имеющие соединенные выходы, могут быть объединены для построения нейросети с прямым распространением. Такие нейросети демонстрируют высокие результаты вследствие композиции нелинейных функций активации при прохождении данных через несколько слоев (так называемое глубокое обучение).

Нейронная сеть прямого распространения

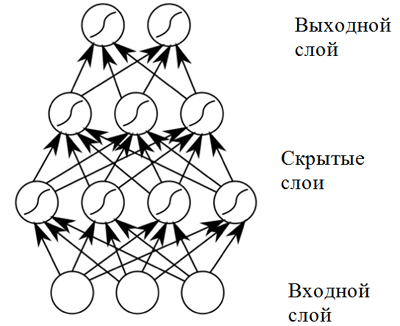
Нейронная сеть прямого распространения демонстрирует хорошие результаты в широком спектре приложений. Однако такая нейросеть имеет один недостаток, не позволяющий использовать ее в задаче, связанной с музыкальной композицией (предсказанием последовательности): она имеет фиксированную размерность входных данных, а музыкальные произведения могут иметь различную длину. Кроме того, нейросети прямого распространения не учитывают входные данные с предыдущих временных шагов, что делает их не слишком полезными для решения задачи предсказания последовательности! Для этой задачи лучше подходит модель, которая называется рекуррентной нейронной сетью.

Рекуррентные нейросети решают обе эти проблемы за счет введения связей между скрытыми узлами: при этом на следующем временном шаге узлы могут получить информацию о данных на предыдущем временном шаге.

Развернутое представление рекуррентной нейронной сети

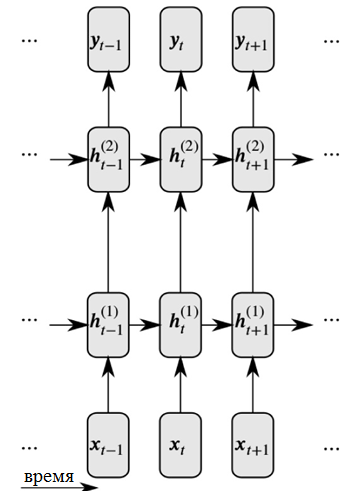
Как можно видеть на рисунке, каждый нейрон теперь принимает входные данные как от предыдущего нейронного слоя, так и с предыдущего момента времени.

Рекуррентные нейросети, имеющие дело с большими входными последовательностями, сталкиваются с так называемой проблемой исчезающего градиента: это означает, что влияние со стороны более ранних временных шагов быстро исчезает. Данная проблема характерна для задачи музыкальной композиции, поскольку в музыкальных произведениях существуют важные долговременные зависимости, которые необходимо учитывать.

Для решения проблемы исчезающего градиента может использоваться модификация рекуррентной сети, которая называется нейронной сетью с долгой краткосрочной памятью (или LSTM-нейросетью). Данная проблема решается с помощью введения ячеек памяти, которые тщательно контролируются тремя типами «вентилей». Перейдите по следующей ссылке для получения дополнительной информации: Общие сведения о LSTM-нейросетях. Таким образом, в BachBot используется модель на основе LSTM-нейросети.

Предварительная обработка

Музыка является очень сложной формой искусства и включает в себя различные размерности: высоту звуков, ритм, темп, динамические оттенки, артикуляцию и прочее. Для упрощения музыки в целях данного проекта рассматриваются только высота и продолжительность звуков. Более того, все хоралы были транспонированы в тональность до мажор (C major) или ля минор (A minor), а длительности нот были отквантованы по времени (округлены) до ближайшего значения, кратного шестнадцатой ноте. Данные действия были предприняты для уменьшения сложности композиций и повышения производительности сети, при этом базовое содержание музыки осталось неизменным. Операции по нормализации тональностей и длительностей нот были выполнены с помощью библиотеки music21.

def standardize_key(score):     """Converts into the key of C major or A minor.     Adapted from https://gist.github.com/aldous-rey/68c6c43450517aa47474      """     # conversion tables: e.g. Ab -> C is up 4 semitones, D -> A is down 5 semitones     majors = dict([("A-", 4),("A", 3),("B-", 2),("B", 1),("C", 0),("C#",-1),                ("D-", -1),("D", -2),("E-", -3),("E", -4),("F", -5),("F#",6),               ("G-", 6), ("G", 5)])     minors = dict([("A-", 1),("A", 0),("B-", -1),("B", -2),("C", -3),("C#",-4),             ("D-", -4),("D", -5),("E-", 6),("E", 5),("F", 4),("F#",3),                  ("G-",3),("G", 2)])       # transpose score     key = score.analyze('key')     if key.mode == "major":         halfSteps = majors[key.tonic.name]     elif key.mode == "minor":         halfSteps = minors[key.tonic.name]     tScore = score.transpose(halfSteps)       # transpose key signature     for ks in tScore.flat.getKeySignatures():         ks.transpose(halfSteps, inPlace=True)     return tScore 

Код, используемый для стандартизации ключевых знаков в собрании сочинений, на выходе используются тональности до мажор (C major) или ля минор (A minor)

Квантование по времени до ближайшего значения, кратного шестнадцатой ноте, было выполнено с помощью функции Stream.quantize() библиотеки music21. Ниже приведено сравнение статистики, связанной с набором данных до и после его предварительной обработки:

Использование каждого класса нот до (слева) и после предварительной обработки (справа). Класс нот представляет собой ноту независимо от ее октавы

Расположение нот до (слева) и после предварительной обработки (справа)

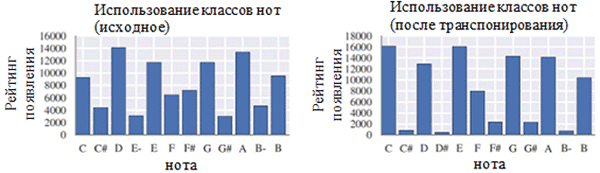
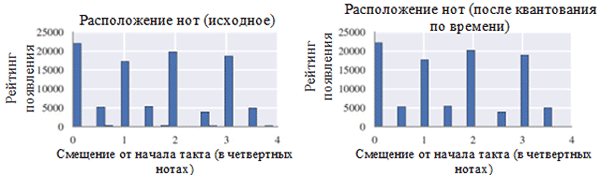
Как можно видеть на рисунке сверху, транспозиция исходной тональности хоралов в тональность до мажор (C major) или ля минор (A minor) значительно повлияла на класс нот, используемых в собрании сочинений. В частности, увеличилось число вхождений для нот в тональностях до мажор (C major) и ля минор (A minor) (C, D, E, F, G, A, B). Также можно наблюдать небольшие пики для нот F# и G# из-за их присутствия в восходящей последовательности мелодического ля минора (A, B, C, D, E, F# и G#). С другой стороны, квантование по времени оказало значительно меньший эффект. Это можно объяснить высоким разрешением квантования (аналогично округлению до множества значимых цифр).

Кодирование

После того, как данные прошли предварительную обработку, необходимо закодировать хоралы в формат, который может быть легко обработан с помощью рекуррентной нейросети. Требуемый формат является последовательностью токенов. Для проекта BachBot было выбрано кодирование на уровне нот (каждый токен представляет собой ноту) вместо уровня аккордов (каждый токен представляет собой аккорд). Такое решение сократило размер словаря со 128⁴ возможных аккордов до 128 возможных нот, что позволило повысить эффективность работы.

Для проекта BachBot была создана оригинальная схема кодирования музыкальных композиций. Хорал разбивается на временные шаги, соответствующие шестнадцатым нотам. Данные шаги называются кадрами. Каждый кадр содержит последовательность кортежей, представляющих собой значение высоты ноты в формате цифрового интерфейса музыкальных инструментов (MIDI) и признак привязки данной ноты к предыдущей ноте такой же высоты (нота, признак привязки). Ноты в пределах кадра нумеруются в нисходящем порядке по высоте (сопрано ? альт ? тенор ? бас). Каждый кадр также может иметь фермату, обозначающую конец фразы; фермата представлена символом точки (.) над нотой. Символы START и END добавляются в начало и конец каждого хорала. Данные символы вызывают инициализацию модели и позволяют пользователю определить момент окончания композиции.

START
(59, True)
(56, True)
(52, True)
(47, True)
|||
(59, True)
(56, True)
(52, True)
(47, True)
|||
(.)
(57, False)
(52, False)
(48, False)
(45, False)
|||
(.)
(57, True)
(52, True)
(48, True)
(45, True)
|||
END
Пример кодирования двух аккордов. Каждый аккорд длится восьмую долю такта, второй аккорд сопровождается ферматой. Последовательность «|||» обозначает конец кадра

def encode_score(score, keep_fermatas=True, parts_to_mask=[]):     """     Encodes a music21 score into a List of chords, where each chord is represented with     a (Fermata :: Bool, List[(Note :: Integer, Tie :: Bool)]).     If `keep_fermatas` is True, all `has_fermata`s will be False.     All tokens from parts in `parts_to_mask` will have output tokens `BLANK_MASK_TXT`.     Time is discretized such that each crotchet occupies `FRAMES_PER_CROTCHET` frames.     """     encoded_score = []     for chord in (score             .quantize((FRAMES_PER_CROTCHET,))             .chordify(addPartIdAsGroup=bool(parts_to_mask))             .flat             .notesAndRests): # aggregate parts, remove markup         # expand chord/rest s.t. constant timestep between frames         if chord.isRest:             encoded_score.extend((int(chord.quarterLength * FRAMES_PER_CROTCHET)) * [[]])         else:             has_fermata = (keep_fermatas) and any(map(lambda e: e.isClassOrSubclass(('Fermata',)), chord.expressions))               encoded_chord = []             # TODO: sorts Soprano, Bass, Alto, Tenor without breaking ties             # c = chord.sortAscending()             # sorted_notes = [c[-1], c[0]] + c[1:-1]             # for note in sorted_notes:             for note in chord:                 if parts_to_mask and note.pitch.groups[0] in parts_to_mask:                     encoded_chord.append(BLANK_MASK_TXT)                 else:                     has_tie = note.tie is not None and note.tie.type != 'start'                     encoded_chord.append((note.pitch.midi, has_tie))             encoded_score.append((has_fermata, encoded_chord))               # repeat pitches to expand chord into multiple frames             # all repeated frames when expanding a chord should be tied             encoded_score.extend((int(chord.quarterLength * FRAMES_PER_CROTCHET) - 1) * [                 (has_fermata,                     map(lambda note: BLANK_MASK_TXT if note == BLANK_MASK_TXT else (note[0], True), encoded_chord))             ])     return encoded_score

Код, используемый для кодирования тональности music21 с помощью специальной схемы кодирования

Задание модели

В предыдущей части было приведено объяснение, показывающее, что задача автоматической композиции может быть сведена к задаче предсказывания последовательности. В частности, модель может предсказывать наиболее вероятную следующую ноту на основе предыдущих нот. Для решения задачи данного типа лучше всего подходит нейронная сеть с долгой краткосрочной памятью (LSTM). Формально модель должна предсказывать P(x_t+1 | x_t, h_t-1), распределение вероятностей для следующих возможных нот (x_t+1) на основе текущего токена (x_t) и предыдущего скрытого состояния (h_t-1). Интересно, что ту же самую операцию выполняют языковые модели на базе рекуррентных нейронных сетей.

В режиме композиции модель инициализируется с помощью токена START, после чего выбирает следующий наиболее вероятный токен для следования по нему. После этого модель продолжает выбирать следующий наиболее вероятный токен с помощью предыдущей ноты и предыдущего скрытого состояния до тех пор, пока не будет сгенерирован токен END. В системе присутствуют температурные элементы, добавляющие некоторую степень случайности, чтобы не допустить со стороны BachBot сочинения той же самой пьесы снова и снова.

Функция потери

При обучении модели для предсказания, обычно существует некоторая функция, которая должна быть минимизирована (называемая функцией потери). Данная функция описывает разницу между предсказанием модели и свойством ground truth. BachBot минимизирует потерю перекрестной энтропии между предсказанным распределением (x_t+1) и фактическим распределением целевой функции. Использование перекрестной энтропии в качестве функции потери — хорошая отправная точка для широкого диапазона задач, однако в некоторых случаях вы можете использовать свою собственную функцию потери. Другой допустимый подход заключается в попытке использования различных функций потери и применении той модели, которая минимизирует фактическую потерю в ходе проверки.

Обучение/тестирование

В ходе обучения рекурсивной нейросети BachBot использовал коррекцию токена значением x_t+1 вместо применения предсказания модели. Данный процесс, известный как принудительное обучение, используется для обеспечения сходимости, поскольку предсказания модели, естественно, будут давать плохие результаты в начале обучения. Напротив, во время проведения проверки и композиции предсказание модели x_t+1 следует использовать повторно в качестве входных данных для следующего предсказания.

Иные соображения

Для повышения эффективности в данной модели использовались следующие практические методы, общие для LSTM-нейросетей: нормализованное усечение градиента, метод исключения, нормализация пакета и метод усеченного обратного распространения ошибки во времени (BPTT).

Метод нормализованного усечения градиента устраняет проблему неуправляемого роста значения градиента (обратную проблеме исчезающего градиента, которая была решена с помощью использования архитектуры ячеек LSTM-памяти). При использовании данной техники значения градиента, превышающие определенный порог, усекаются или масштабируются.

Метод исключения представляет собой технику, при которой некоторые нейроны, выбранные случайным образом, отключаются (исключаются) во время обучения сети. Это позволяет избежать сверхподгонки и повысить качество обобщения. Проблема сверхподгонки возникает в том случае, когда модель становится оптимизированной для обучающего набора данных и в меньшей степени применимой для образцов за пределами этого набора. Метод исключения зачастую ухудшает потерю при выполнении обучения, однако улучшает ее на этапе проверки (подробнее об этом ниже).

Вычисление градиента в рекуррентной нейросети для последовательности длиной в 1000 элементов эквивалентно по затратам прямому и обратному проходу в нейросети прямого распространения из 1000 слоев. Метод усеченного обратного распространения ошибки (BPTT) во времени используется для сокращения затрат на обновление параметров в процессе обучения. Это означает, что ошибки распространяются только в течение фиксированного количества временных шагов, отсчитываемых назад от текущего момента. Обратите внимание, что долговременные зависимости при обучении по-прежнему возможны при использовании метода BPTT, поскольку скрытые состояния уже были проявлены на множестве предыдущих временных шагов.

Параметры

Далее приведен список релевантных параметров для моделей рекуррентных нейросетей/нейросетей с долгой краткосрочной памятью:

• Количество слоев. При увеличении этого параметра может повыситься эффективность модели, однако для ее обучения потребуется больше времени. Кроме того, слишком большое число слоев может привести к сверхподгонке.
• Размерность скрытого состояния. При увеличении этого параметра может повыситься сложность модели, однако это может привести к сверхподгонке.
• Размерность векторных сопоставлений
• Длина последовательности/количество кадров перед выполнением усечения обратного распространения ошибки во времени.
• Вероятность исключения нейронов. Вероятность, с которой нейрон будет исключен из работы сети при каждом цикле обновления.

Методика подбора оптимального набора параметров будет рассмотрена далее в этой статье.

Реализация, обучение и тестирование

Выбор платформы

В настоящее время существует множество платформ, позволяющих реализовать модели машинного обучения на различных языках программирования (включая даже JavaScript!). Среди популярных платформ — scikit-learn, TensorFlow и Torch. В качестве платформы для проекта BachBot была выбрана библиотека Torch. Сначала была испробована библиотека TensorFlow, однако на тот момент в ней использовались развернутые рекуррентные нейросети, которые приводили к переполнению оперативной памяти графического процессора. Torch представляет собой научную вычислительную платформу, работающую на быстром языке программирования LuaJIT*. Платформа Torch содержит превосходные библиотеки для работы с нейросетями и оптимизацией.

Реализация и обучение модели

Реализация, очевидно, будет различаться в зависимости от языка и платформы, на которых вы остановите свой выбор. Чтобы узнать, как в BachBot реализованы нейросети с долгой краткосрочной памятью с использованием Torch, ознакомьтесь со скриптами, использованными для обучения и задания параметров BachBot. Данные скрипты доступны на сайте GitHub Фейнмана Лянга Хорошей отправной точкой для навигации по репозиторию является скрипт 1-train.zsh. С помощью него вы сможете найти путь к файлу bachbot.py. Точнее говоря, основным скриптом для задания параметров модели является файл LSTM.lua. Скриптом для обучения модели является файл train.lua.

Оптимизация гиперпараметров

Для поиска оптимальных значений гиперпараметров использовался метод поиска по сетке с применением нижеуказанной сетки параметров.

Сетка параметров, использованных BachBot при поиске по сетке

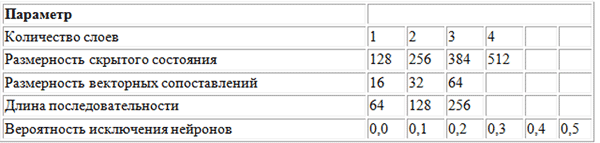
Поиск по сетке представляет собой полный перебор всех возможных сочетаний параметров. Другими предлагаемыми методами оптимизации гиперпараметров являются случайный поиск и байесовская оптимизация.

Оптимальный набор гиперпараметров, обнаруженный в результате поиска по сетке, выглядит следующим образом: количество слоев = 3, размерность скрытого состояния = 256, размерность векторных сопоставлений = 32, длина последовательности = 128, вероятность исключения нейронов = 0,3.

Данная модель достигла значения потери перекрестной энтропии 0,324 в ходе обучения и 0,477 на этапе проверки. График кривой обучения демонстрирует, что процесс обучения сходится через 30 итераций (?28,5 минут при использовании одного графического процессора).

Графики потери в ходе обучения и на этапе проверки также могут проиллюстрировать влияние каждого гиперпараметра. Особый интерес для нас представляет вероятность исключения нейронов:

Кривые обучения для различных настроек метода исключения

На рисунке можно видеть, что метод исключения действительно позволяет избежать возникновения сверхподгонки. Хотя при значении вероятности исключения в 0,0 потеря в ходе обучения минимальна, на этапе проверки потеря имеет максимальное значение. Большие значения вероятности приводят к увеличению потерь в ходе обучения и уменьшению потерь на этапе проверки. Минимальное значение потери на этапе проверки при работе с BachBot было зафиксировано при вероятности исключения, равной 0,3.

Альтернативные методы оценки (опционально)

Для некоторых моделей — особенно для таких творческих приложений, как сочинение музыки — потеря может не являться подходящей мерой успешной работы системы. Вместо этого лучшим критерием может стать субъективное человеческое восприятие.

Целью проекта BachBot является автоматическое сочинение музыки, которая неотличима от собственных композиций Баха. Для оценки успешности полученных результатов проводился опрос пользователей в Интернете. Опросу была придана форма конкурса, в котором пользователям предлагалось определить, какие произведения принадлежат проекту BachBot, а какие — Баху.

Результаты опроса показали, что участники опроса (759 человек с различным уровнем подготовки) смогли точно различить два образца только в 59 процентах случаев. Это всего лишь на 9 процентов выше результата случайного угадывания! Попробуйте пройти опрос BachBot самостоятельно!

Адаптация модели к гармонизации

Теперь BachBot может вычислять P(x_t+1 | x_t, h_t-1), распределение вероятностей для следующих возможных нот на основе текущей ноты и предыдущего скрытого состояния. Данная последовательная модель предсказаний может быть впоследствии адаптирована для гармонизации мелодии. Такая адаптированная модель требуется для гармонизации мелодии, модулированной с помощью эмоций, в рамках музыкального проекта с отображением слайдов.

При работе с гармонизацией модели предоставляется заранее заданная мелодия (обычно это партия сопрано), а модель после этого должна сочинить музыку для остальных частей. Для выполнения этой задачи используется жадный поиск «лучший-первый» с ограничением на то, что ноты мелодии являются фиксированными. Жадные алгоритмы задействуют принятие решений, которые являются оптимальными с локальной точки зрения. Итак, ниже описана простая стратегия, используемая для гармонизации:

Допустим, что x_t представляют собой токены в предлагаемой гармонизации. На временном шаге t, если нота соответствует мелодии, то x_t равно данной ноте. В противном случае x_t равно наиболее вероятной следующей ноте в соответствии с предсказаниями модели. Код для такой адаптации модели можно найти на сайте GitHub Фейнмана Лянга: HarmModel.lua, harmonize.lua.

Ниже приведен пример гармонизации колыбельной Twinkle, Twinkle, Little Star с помощью BachBot, при этом использовалась вышеуказанная стратегия.

Гармонизация колыбельной Twinkle, Twinkle, Little Star с помощью BachBot (в партии сопрано). Партии альта, тенора и баса также были заполнены с помощью BachBot

В данном примере мелодия колыбельной Twinkle, Twinkle, Little Star приведена в партии сопрано. После этого партии альта, тенора и баса были заполнены с помощью BachBot с использованием стратегии гармонизации. А вот, как это звучит. Несмотря на то, что BachBot продемонстрировал неплохую эффективность при выполнении данной задачи, существуют определенные ограничения, связанные с этой моделью. Точнее говоря, алгоритм не заглядывает вперед в мелодию и использует только текущую ноту мелодии и прошлый контекст для генерации последующих нот. При гармонизации мелодии людьми они могут охватить всю мелодию целиком, что упрощает вывод подходящих гармонизаций. Тот факт, что данная модель не способна этого делать, может привести к неожиданностям из-за ограничений использования последующей информации, которые являются причиной ошибок. Для решения этой проблемы может использоваться так называемый лучевой поиск.

При использовании лучевого поиска проверяются различные линии движения. Например вместо использования только одной, наиболее вероятной ноты, что делается в настоящий момент, могут рассматриваться четыре или пять наиболее вероятных нот, после чего алгоритм продолжает свою работу с каждой из этих нот. Рассмотрение различных вариантов может помочь модели восстановиться после появления ошибок. Лучевой поиск обычно используется в приложениях для обработки естественного языка для создания предложений.

Мелодии, смодулированные с помощью эмоций, теперь могут быть пропущены через такую модель гармонизации для их завершения.