Нейронные сети, фундаментальные принципы работы, многообразие и топология
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2018-07-04 09:41
Понять поведение глубоких нейронных сетей в целом нетривиальная задача. Проще исследовать низкоразмерные глубокие нейронные сети — сети, в которых есть только несколько нейронов в каждом слое. Для низкоразмерных сетей можно создавать визуализацию, чтобы понять поведение и обучение таких сетей. Эта перспектива позволит получить более глубокое понимание о поведении нейронных сетей и наблюдать связь, объединяющую нейронные сети с областью математики, называемой топологией.
Из этого вытекает ряд интересных вещей, в том числе фундаментальные нижние границы сложности нейронной сети, способной классифицировать определенные наборы данных.
Рассмотрим принцип работы сети на примере
Начнем с простого набора данных — двух кривых на плоскости. Задача сети научится классифицировать принадлежность точек кривым.
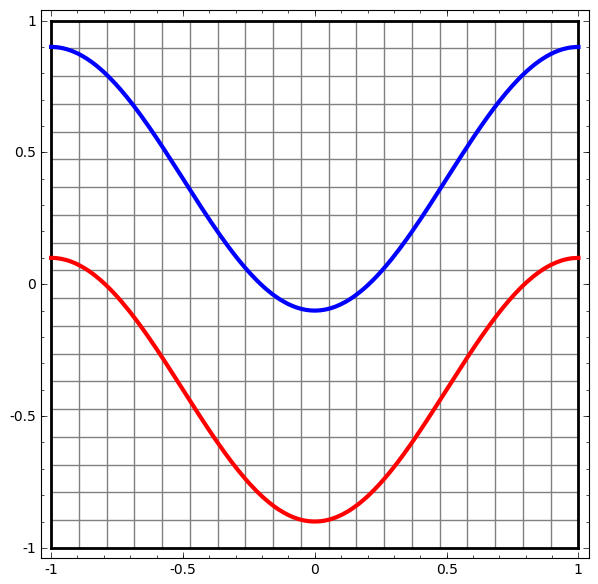
Начнем с простейшего класса нейронной сети, с одним входным и выходным слоем. Такая сеть пытается отделить два класса данных, разделив их линией.
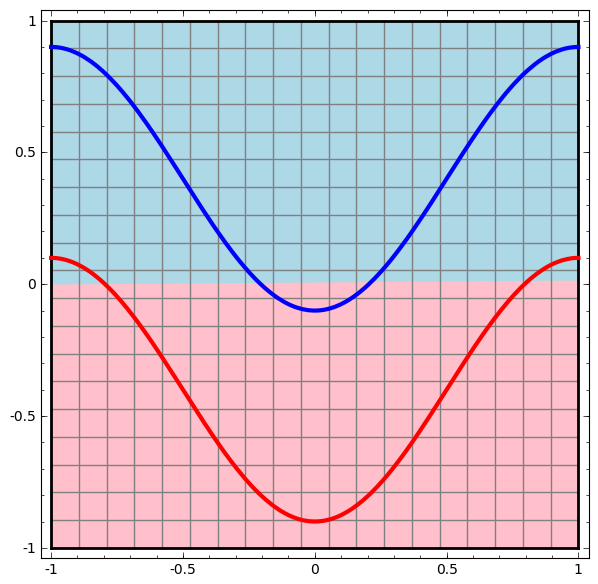
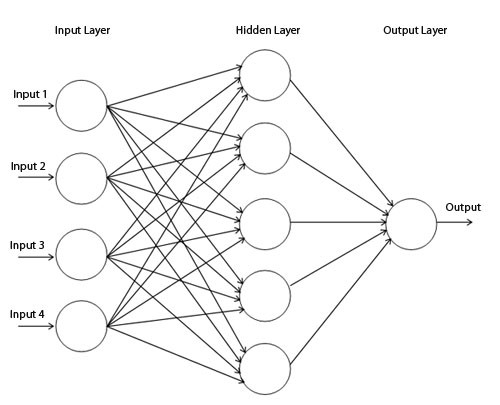
Схема простой сети
Визуализируем поведение этой сети, наблюдая за тем, что она делает с разными точками в своей области. Сеть со скрытым слоем отделяет данные более сложной кривой, чем линия.
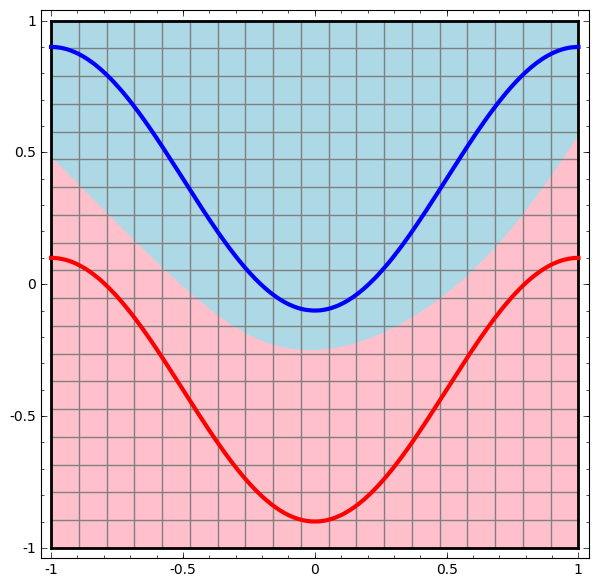
В предыдущей визуализации рассмотрены данные в «сыром» представлении. Вы можете представить это, посмотрев на входной слой. Теперь, рассмотрим его после того, как он будет преобразован первым слоем. Вы можете представить это, посмотрев на скрытый слой.
Каждое измерение соответствует активации нейрона в слое.
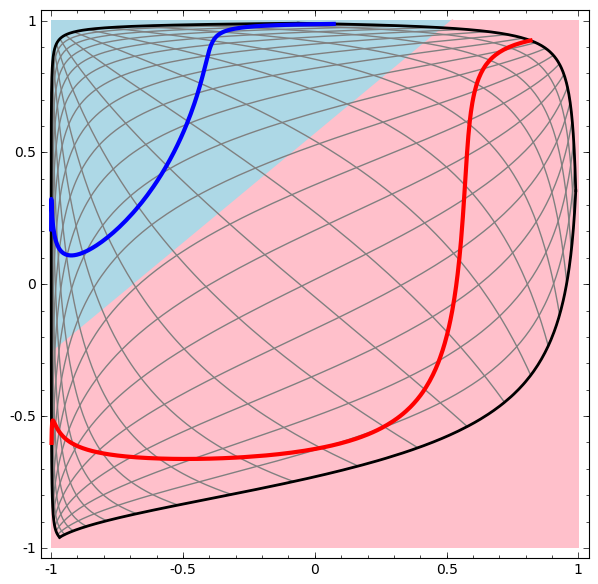
Непрерывная визуализация слоев
В подходе, описанном в предыдущем разделе, мы учимся понимать сети, просматривая представление, соответствующее каждому слою. Это дает нам дискретный список представлений.
Нетривиальная часть заключается в понимании того, как мы переходим от одного к другому. К счастью, уровни нейронной сети имеют свойства, которые делают это возможным.
Существует множество различных типов слоёв, используемых в нейронных сетях.
Рассмотрим слой tanh для конкретного примера. Tanh-слой tanh (Wx + b) состоит из:
- Линейного преобразование «весовой» матрицей W
- Перевод с помощью вектора b
- Точечное применение tanh.
Мы можем представить это как непрерывное преобразование следующим образом:
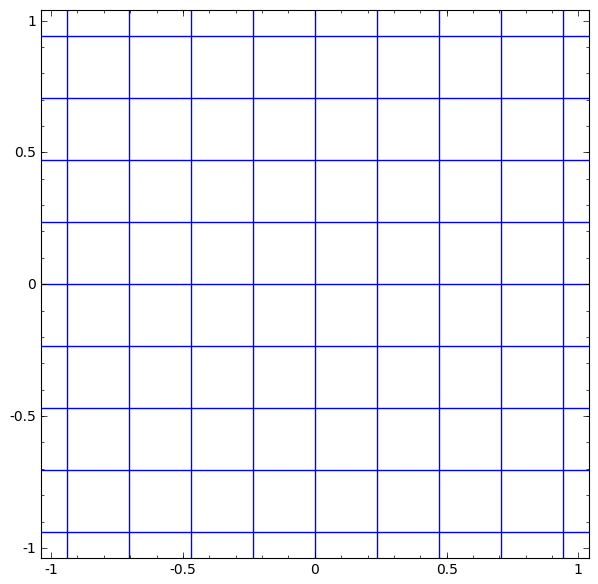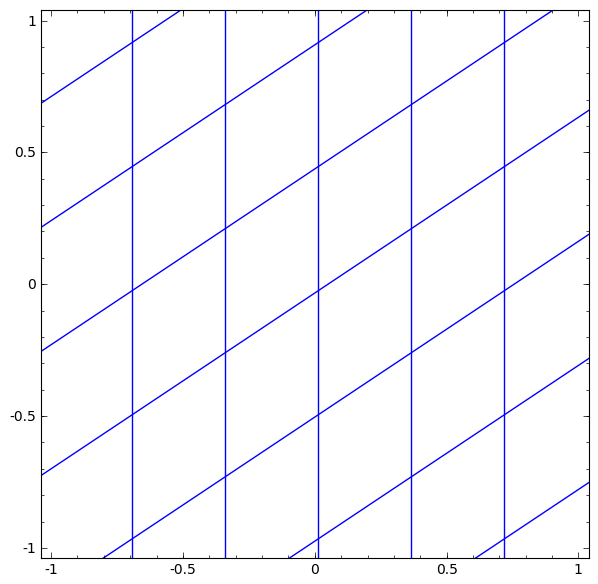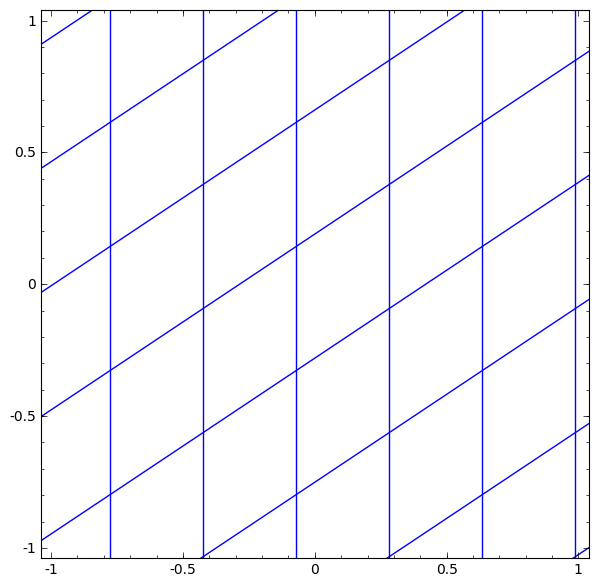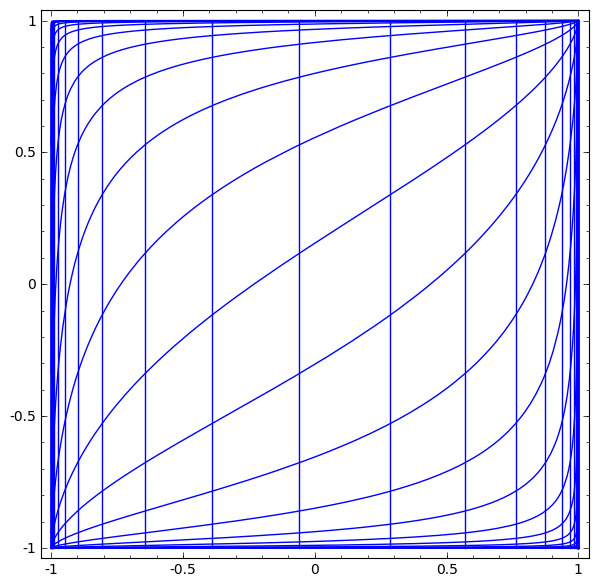
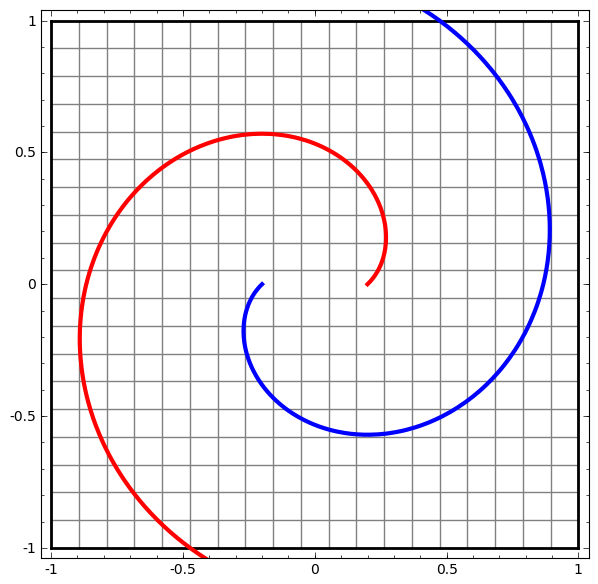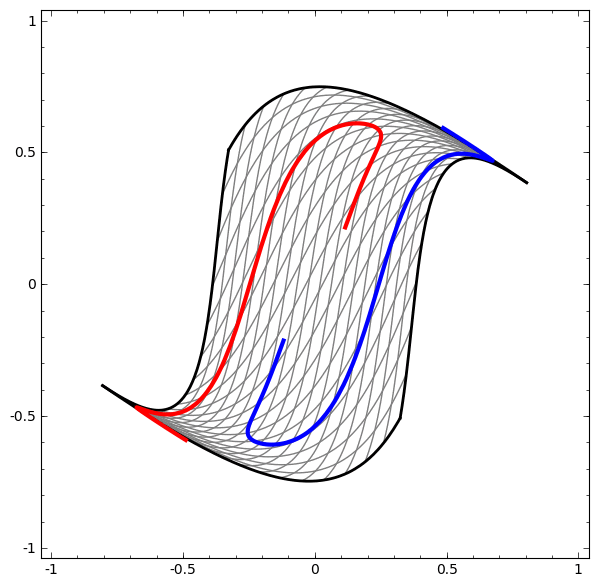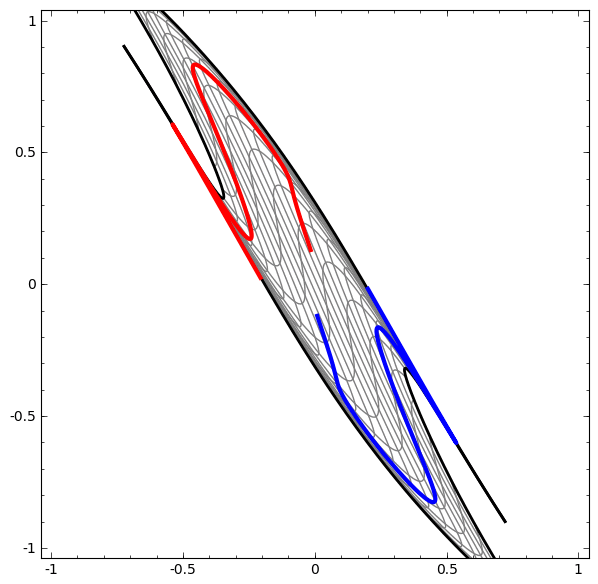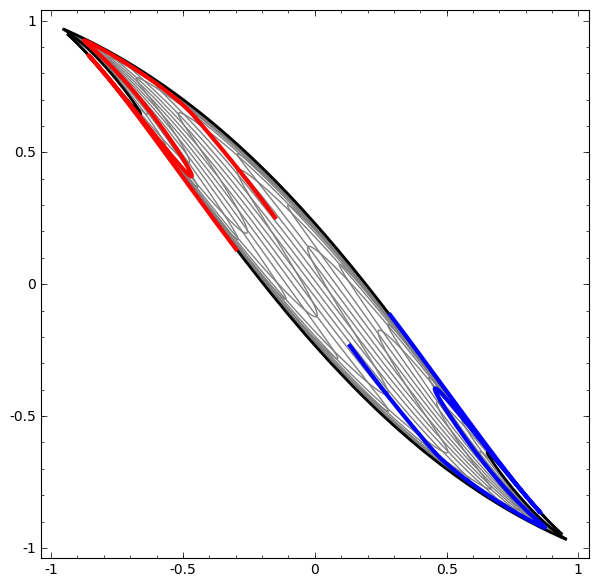
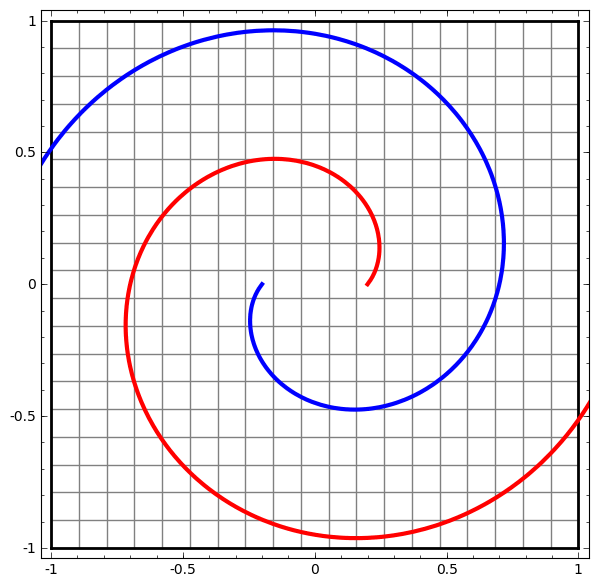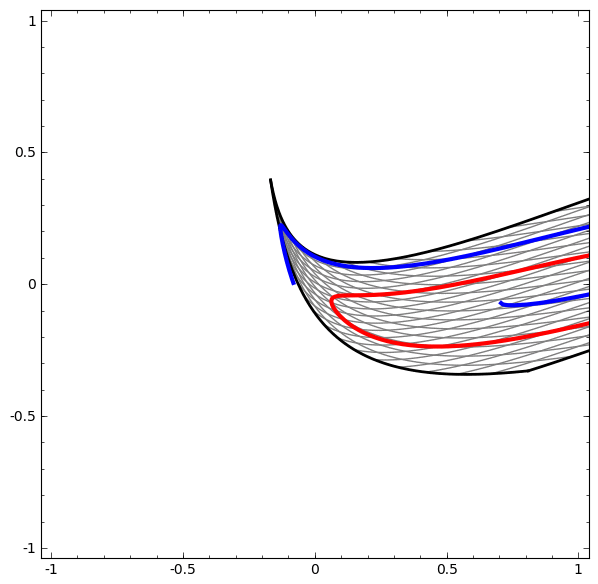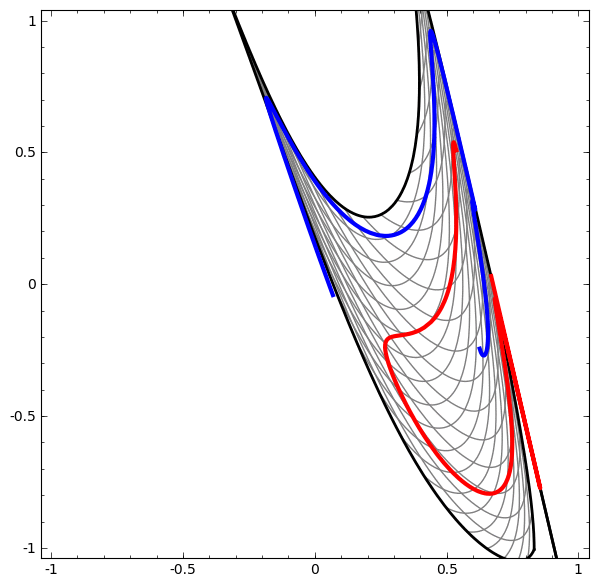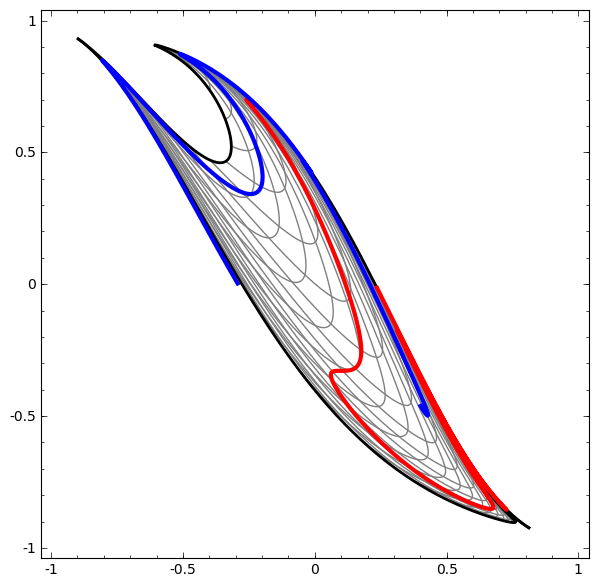
Топология слоев tang
Каждый слой растягивается и сжимает пространство, но он никогда не режет, не разбивает и не складывает его. Интуитивно мы видим, что топологические свойства сохраняются на каждом слое.
Такие преобразования, которые не влияют на топологию, называются гомоморфизмами (Wiki — Это отображение алгебраической системы А, сохраняющее основные операции и основные отношения). Формально они являются биекциями, которые являются непрерывными функциями в обоих направлениях. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством.
Теорема
Слои с N входами и N выводами являются гомоморфизмами, если весовая матрица W не является вырожденной. (Нужно быть осторожным в отношении домена и диапазона.)
1. Предположим, что W имеет ненулевой детерминант. Тогда это биективная линейная функция с линейным обратным. Линейные функции непрерывны. Итак, умножение на W является гомеоморфизмом.
2. Отображения — гомоморфизмы
3. tanh (и сигмоиды и softplus, но не ReLU) являются непрерывными функциями с непрерывными обратными. Они являются биекциями, если мы внимательно относимся к области и диапазону, который мы рассматриваем. Применение их поточечно, является гомоморфизмом.
Таким образом, если W имеет ненулевой детерминант, слой является гомеоморфным.
Топология и классификация
Рассмотрим двухмерный набор данных с двумя классами A, B?R2:
А = {х | d (х, 0) <1/3}
В = {х | 2/3 <d (х, 0) <1}

Требование: нейронная сеть не может классифицировать этот набор данных, не имея 3 или более скрытых слоя, независимо от ширины.
Как упоминалось ранее, классификация с сигмовидной функцией или слоем softmax эквивалентна попытке найти гиперплоскость (или в этом случае линию), которая разделяет A и B в конечном представлении. Имея только два скрытых слоя, сеть топологически неспособна разделять данные таким образом, и обречена на неудачу в этом наборе данных.
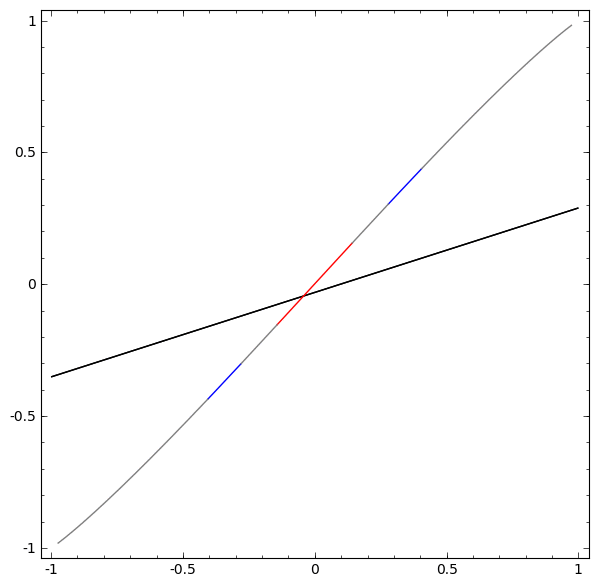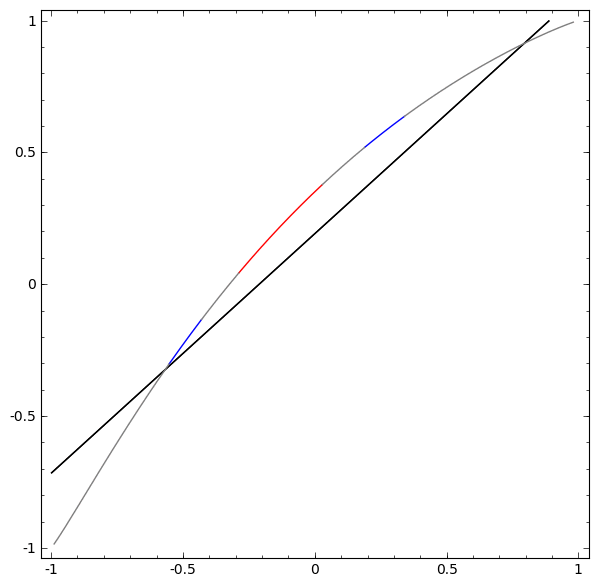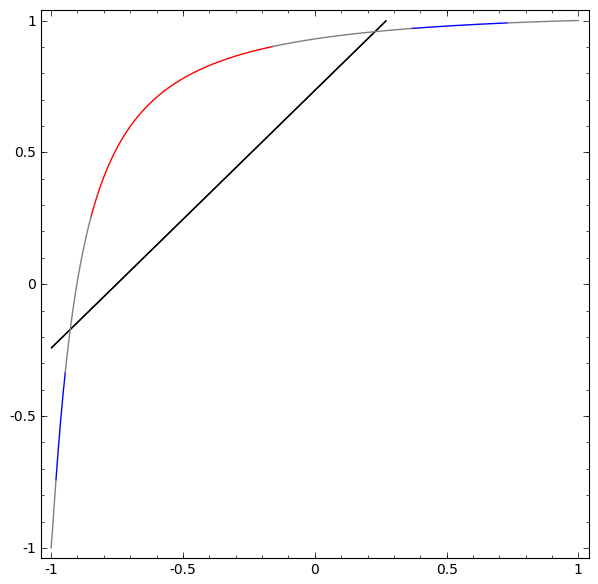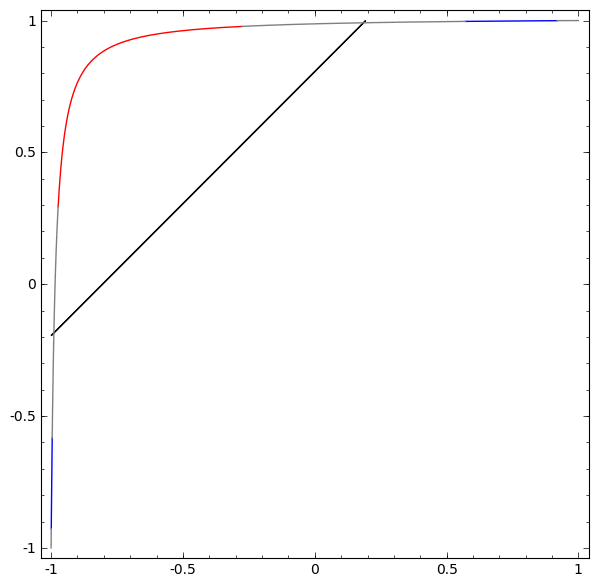
В следующей визуализации мы наблюдаем скрытое представление, пока сеть тренируется вместе с классификационной линией.
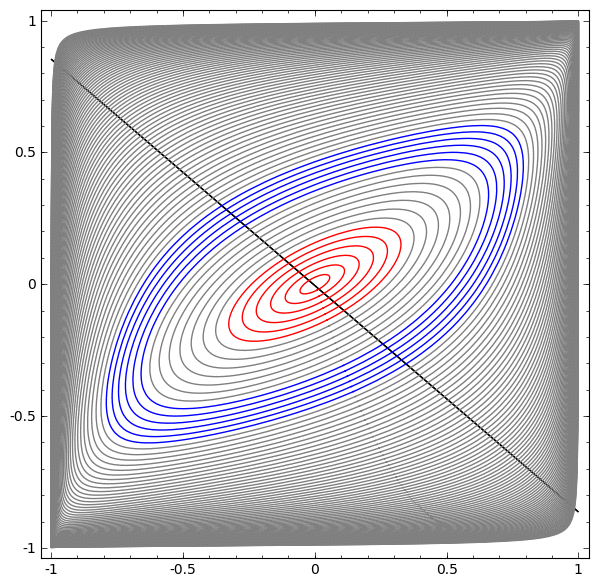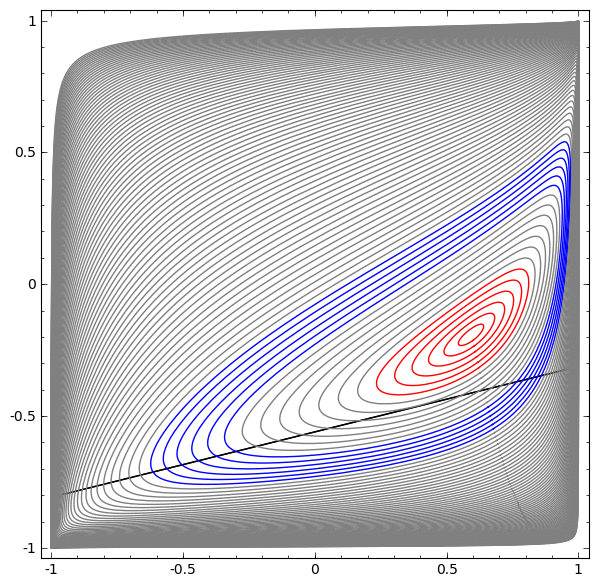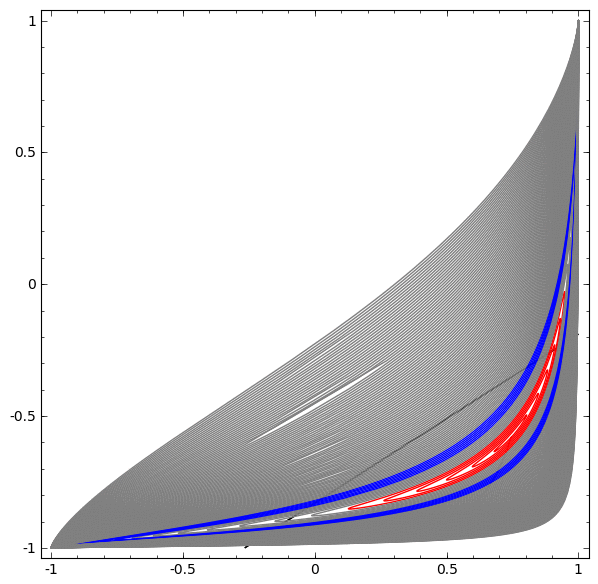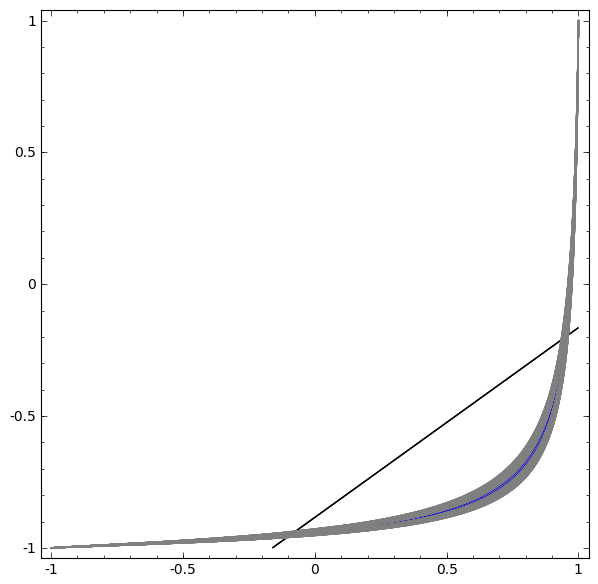
В этом примере был только один скрытый слой, но он не срабатывал.
Утверждение. Либо каждый слой является гомоморфизмом, либо весовая матрица слоя имеет определитель 0.
Если это гомоморфизм, то A по-прежнему окружен B, и линия не может их разделить. Но предположим, что она имеет детерминант 0: тогда набор данных коллапсирует на некоторой оси. Поскольку мы имеем дело с чем-то, гомеоморфным исходному набору данных, A окруженных B, и коллапсирование на любой оси означает, что мы будем иметь некоторые точки из A и B смешенными, и что приводит к невозможности для различения.
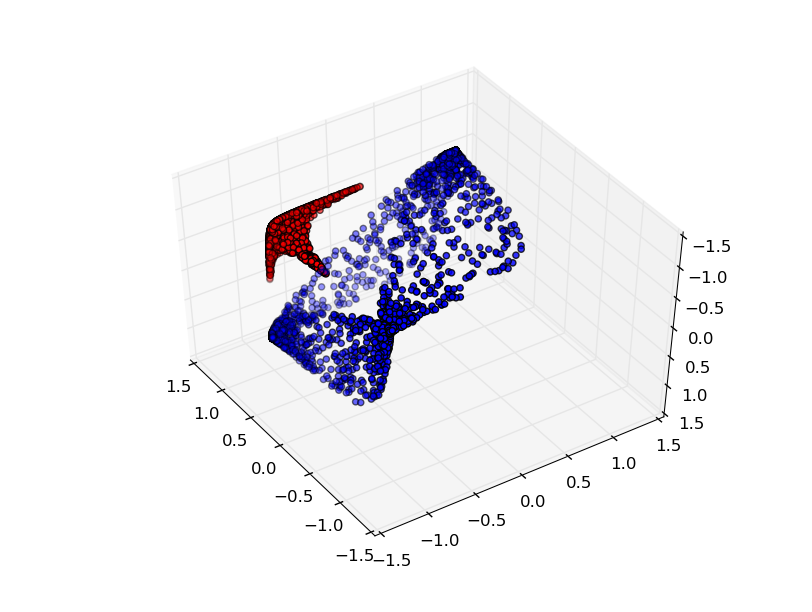

Без использования слоя из двух или более скрытых элементов мы не можем классифицировать этот набор данных. Но, если мы используем сеть с двумя элементами, мы научимся представлять данные как хорошую кривую, которая позволяет нам разделять классы с помощью линии:
Гипотеза многообразия
Это относится к наборам данных из реального мира, например, наборам изображений? Если вы серьезно относитесь к гипотезе многообразия, я думаю, что это имеет значение.
Многомерная гипотеза состоит в том, что естественные данные образуют низкоразмерные многообразия в пространстве имплантации. Есть и теоретические [1], и экспериментальные[2] причины полагать, что это правда. Если это так, то задача алгоритма классификации состоит в том, чтобы отделить пучок запутанных многообразий.
В предыдущих примерах один класс полностью окружал другой. Тем не менее маловероятно, что многообразие изображений собак полностью окружены коллекцией изображений кошек. Но есть и другие, более правдоподобные топологические ситуации, которые все еще могут возникнуть, как мы увидим в следующем разделе.
Связи и гомотопии
Еще один интересный набор данных — два связанных тора A и B.

Связи изучаются в теории узлов, области топологии. Иногда, когда мы видим связь, не сразу понятно, является ли это бессвязность (множество вещей, которые запутались вместе, но могут быть разделены непрерывной деформацией) или нет.
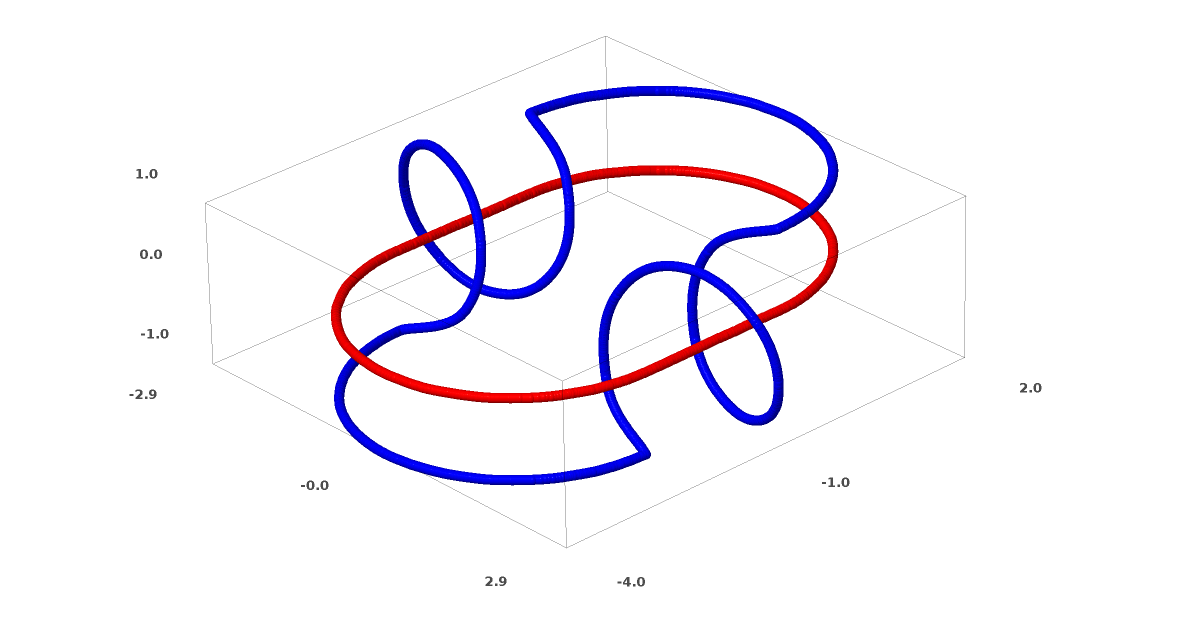
Если нейронная сеть, использующая слои только с тремя юнитами, может ее классифицировать, то она является бессвязной. (Вопрос: Может ли все бессвязности классифицироваться по сети только с тремя бессвязностями, теоретически?)
С точки зрения этого узла, непрерывная визуализация представлений, созданных нейронной сетью, это процедура распутывания связей. В топологии мы будем называть это эмбиентной изотопией между исходным звеном и разделенными.
Формально, изотопия окружающего пространства между многообразиями А и В является непрерывной функцией F: [0,1] ? X ? Y такая, что каждый Ft является гомеоморфизмом из X в его диапазон, F0 является тождественной функцией, а F1 отображает A в B. Т.е. Ft непрерывно переходит из отображения A в себя, к отображению A в B.
Теорема: существует изотопия окружающего пространства между входом и представлением сетевого уровня, если: a) W не является вырожденной, b) мы готовы перенести нейроны в скрытый слой и c) имеется более 1 скрытого элемента.
1. Самая сложная часть — линейное преобразование. Чтобы это было возможно, нам нужно, чтобы W обладала положительным определителем. Наша предпосылка заключается в том, что она не равна нулю, и мы можем перевернуть знак, если он отрицательный, переключив два скрытых нейрона, и поэтому можем гарантировать, что определитель положителен. Пространство положительных детерминантных матриц является связным, поэтому существует p: [0,1] ? GLn ®5 такое, что p (0) = Id и p (1) = W. Мы можем непрерывно переходить от функции тождества к W-преобразованию с помощью функции x ? p (t) x, умножая x в каждой точке времени t на непрерывно переходящую матрицу p (t).
2. Мы можем непрерывно переходить от функции тождества к b-отображению с помощью функции x ? x + tb.
3. Мы можем непрерывно переходить от тождественной функции к поточечному использованию ? с функцией: x ? (1-t) x + t? (x)
Связи и узлы являются одномерными многообразиями, но нам нужны 4 измерения, чтобы сети могли распутать все из них. Точно так же может потребоваться еще более высоко размерное пространство, чтобы иметь возможность разложить n-мерные многообразия. Все n-мерные многообразия могут быть разложены в 2n + 2 размерностях. [3]
Легкий выход
Простой путь, состоит в том, чтобы попытаться вытащить многообразия отдельно и растянуть части, которые запутаны настолько, насколько это возможно. Хотя это не будет близко к подлинному решению, такое решение может достичь относительно высокой точности классификации и быть приемлемым локальным минимумом.

С другой стороны, если нас интересует исключительно достижение хороших результатов классификации, подход приемлем. Если крошечный бит многообразия данных зацепился за другое многообразие, является ли это проблемой? Вероятно, что удастся получить произвольно хорошие результаты классификации, несмотря на эту проблему.
Улучшенные слои для манипулирования многообразиями?
Трудно представить, что стандартные слои с аффинным преобразованием, действительно, хороши для манипулирования многообразиями.
Возможно, имеет смысл иметь совсем другой слой, который мы можем использовать в композиции с более традиционными?
Перспективным является изучение векторного поля с направлением, в котором мы хотим сдвинуть многообразие:

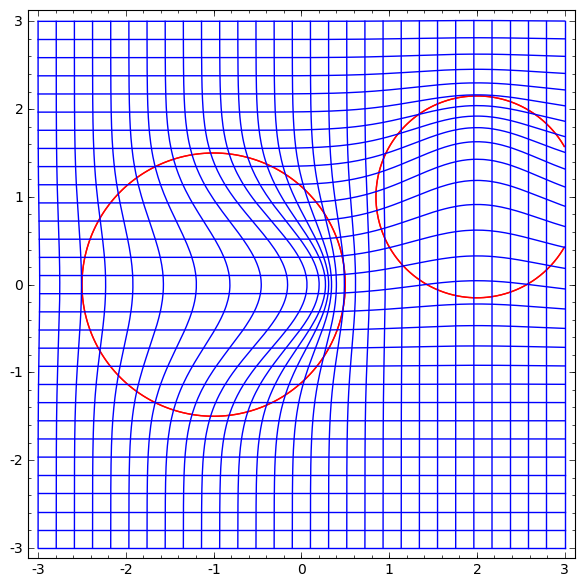
Р (х) =( v0f0 (х) + v1f1 (х) )/( 1 + 0 (х) + f1 (х))
K-Nearest Neighbor Layers
Линейная разделимость может быть огромной и, возможно, необоснованной потребностью в нейронных сетях. Естественным является применение метода k-ближайших соседей (k-NN). Однако, успех k-NN в значительной степени зависит от представления, которое он классифицирует, поэтому требуется хорошее представление до того, как k-NN сможет работать хорошо.
k-NN дифференцируема по отношению к представлению, на которое оно действует. Таким образом, мы можем напрямую обучать сеть для классификации k-NN. Это можно рассматривать как своего рода слой «ближайшего соседа», который действует как альтернатива softmax.
Мы не хотим предуправлять всем нашим набором тренировок для каждой мини-партии, потому что это будет очень дорогостоящей процедурой. Адаптированный подход состоит в том, чтобы классифицировать каждый элемент мини-партии на основе классов других элементов мини-партии, давая каждому вес единицы делённой на расстояние от цели классификации.
К сожалению, даже при сложной архитектуре использование k-NN снижает вероятность ошибки — и использование более простых архитектур ухудшает результаты.
Заключение
Топологические свойства данных, такие как связи, могут сделать невозможным линейное разделение классов с использованием низкоразмерных сетей независимо от глубины. Даже в тех случаях, когда это технически возможно. Например, спирали, разделить которые это может быть очень сложно.
Для точной классификации данных, нейронным сетям необходимы широкие слои. Кроме того, традиционные слои нейронной сети, плохо подходят для представления важных манипуляций с многообразиями; даже, если бы мы установили весовые коэффициенты вручную, было бы сложным компактно представлять преобразования, которые мы хотим.
[1] A lot of the natural transformations you might want to perform on an image, like translating or scaling an object in it, or changing the lighting, would form continuous curves in image space if you performed them continuously.
[2] Carlsson et al. found that local patches of images form a klein bottle.
[3] This result is mentioned in Wikipedia’s subsection on Isotopy versions.
Источник: habr.com