Cтекинг (Stacking) и блендинг (Blending)

Стекинг (Stacked Generalization или Stacking) — один из самых популярных способов ансамблирования алгоритмов, т.е. использования нескольких алгоритмов для решения одной задачи машинного обучения. Пожалуй, он замечателен уже тем, что постоянно переизобретается новыми любителями анализа данных. Это вполне естественно, его идея лежит на поверхности. Известно, что если обучить несколько разных алгоритмов, то в задаче регрессии их среднее, а в задаче классификации — голосование по большинству, часто превосходят по качеству все эти алгоритмы. Возникает вопрос: почему, собственно, использовать для ансамблирования такие простые операции как усреднение или голосование? Можно же ансамблироование доверить очередному алгоритму (т.н. «метаалгоритму») машинного обучения.

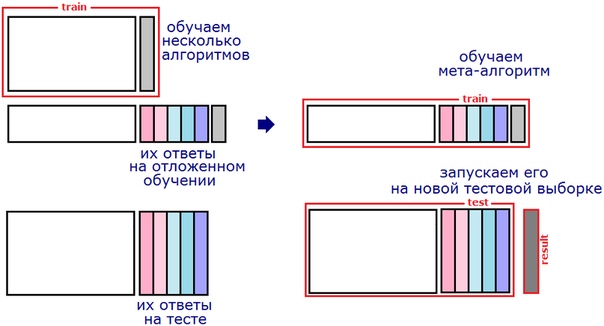
Простейшая схема стекинга — блендинг (Blending): обучающую выборку делят на две части. На первой обучают базовые алгоритмы. Затем получают их ответы на второй части и на тестовой выборке. Понятно, что ответ каждого алгоритма можно рассматривать как новый признак (т.н. «метапризнак»). На метапризнаках второй части обучения настраивают метаалгоритм. Затем запускают его на метапризнаках теста и получают ответ.

Самый большой недостаток блендинга (в описанной реализации) — деление обучающей выборки. Получается, что ни базовые алгоритмы, ни метаалгоритм не используют всего объёма обучения (каждый — только свой кусочек). Понятно, что для повышения качества надо усреднить несколько блендингов с разными разбиениями обучения. Вместо усреднения иногда конкатенируют обучающие (и тестовые) таблицы для метаалгоритма, полученные при разных разбиениях (см. рис. 2): здесь мы получаем несколько ответов для каждого объекта тестовой выборки — их усредняют. На практике такая схема блендинга сложнее в реализации и более медленная, а по качеству может не превосходить обычного усреднения.

Второй способ борьбы за использование всей обучающей выборки — реализация классического стекинга. Ясно, что совсем не делить обучение на подвыборки (т.е. обучить базовые алгоритмы на всей обучающей выборке и потом для всей выборки построить метапризнаки) нельзя: будет переобучение, поскольку в каждом метапризнаке будет «зашита» информация о значении целевого вектора (чтобы понять, представьте, что один из базовых алгоритмов — ближайший сосед). Поэтому выборку разбивают на части (фолды), затем последовательно перебирая фолды обучают базовые алгоритмы на всех фолдах, кроме одного, а на оставшемся получают ответы базовых алгоритмов и трактуют их как значения соответствующих признаков на этом фолде. Для получения метапризнаков объектов тестовой выборки базовые алгоритмы обучают на всей обучающей выборке и берут их ответы на тестовой.

Здесь тоже желательно реализовывать несколько разных разбиений на фолды и затем усреднить соответствующие метапризнаки (или ответы стекингов!). Но самый главный недостаток (классического) стекинга в том, что метапризнаки на обучении (пусть и полноценном — не урезанном) и на тесте разные. Для объяснения возьмём какой-нибудь базовый алгоритм, например, гребневую регрессию. Мета-признак на обучающей выборке — это не ответы какого-то конкретного регрессора, он состоит из кусочков, которые являются ответами разных регрессий (с разными коэффициентами). А метапризнак на контрольной выборке вообще является ответом совсем другой регрессии, настроенной на всём обучениии. В классическом стекинге могут возникать весьма забавные ситуации, когда какой-то метапризнак содержит мало уникальных значений, но множества этих значений на обучении и тесте не пересекаются!

Часто с указанными недостатками борются обычной регуляризацией. Если в качестве метаалгоритма используется гребневая регрессия, то в ней есть соответствующий параметр. А если что-то более сложное (например бустинг над деревьями), то к метапризнакам добавляют нормальный шум. Коэффициент с которым происходит добавка и будет здесь некоторым аналогом коэффициента регуляризации (это очень интересный приём — поиграйтесь на досуге).

Полезно посмотреть работу моего студента Саши Гущина про его попытки (весьма удачные) создать «стекинг без недостатков».

Качество стекинга

Стоит отметить, что не всегда стекинг существенно повышает качество лучшего из базовых алгоритмов. На рис.4 показаны результаты для простейшей модельной задачи (о ней — ниже). Видно, что качество блендинга и стекинга сравнимы с лучшим базовым алгоритмом. Но если этот алгоритм убрать из базовых, качество стекинга падает не сильно.

А вот (рис.4b) качество на случайно взятой реальной задаче (я взял данные проходящего сейчас соревнования mlbootcamp, несколько случайных лесов и LightGBM-ов в качестве базовых алгоритмов).

Также отметим, что здесь мы использовали однократный стекинг (без усреднения), усреднение ещё повышает качество, но незначительно (см. рис. 5-5b).

Кстати, для стекинга нужны достаточно большие выборки(скажем, в двумерных модельных задачах он «начинает работать», когда число объектов измеряется десятками тысяч). На малых выборках он тоже может работать, но тут надо аккуратно подбирать базовые алгоритмы и, главное, метаалгоритм.

Природа алгоритмов

В отличие от бустинга и традиционного бэгинга при стекинге можно (и нужно!) использовать алгоритмы разной природы (например, гребневую регрессию вместе со случайным лесом). Для формирования мета-признаков используют, как правило, регрессоры.

Но стоит помнить о том, что правильное применение стекинга — это не взять кучу разных алгоритмов и «состекать». Дело в том, что для разных алгоритмов нужны разные признаковые пространства. Скажем, если есть категориальные признаки с малым (3-4) числом категорий, то алгоритму «случайный лес» их можно подавать «как есть», а вот для регрессионных (ridge, log_reg) нужно предварительно выполнить one-hot-кодировку.

Метапризнаки

Поскольку это ответы уже натренированных алгоритмов, то они сильно коррелируют. Это априорно один из недостатков подхода. Для борьбы с этим часто базовые алгоритмы не сильно оптимизируют. Иногда здорово срабатывают идеи настройки не на целевой признак, а, например, на разницу между каким-то признаком и целевым.

Стекинг на практике

Стекинг можно и нужно использовать при решении реальных бизнес-задач, поскольку при умелом построении композиции алгоритмов он даже помогает бороться с типичными проблемами реальных данных. Например, одна из таких проблем — значения признаков у нас появляются в реальном времени и в будущем могут быть артефакты, которые мы не наблюдали в прошлом. Скажем, из опыта автора: «сломались» счётчики посещений интернет-ресурсов и начали показывать аномальные значения (в 100 раз больше истины). Это совершенно губит регрессионные алгоритмы (у них ответы также могут возрасти в 100 раз), но если регрессии использовать как базовые алгоритмы (натренировать на разных признаковых пространствах), а в качестве метаалгоритма использовать что-то основанное на деревьях, то ответ такого стекинга уже не будет совсем неадекватным даже при «повреждении» некоторых признаков.

Использование признаков вместе с метапризнаками

Автор знает несколько случаев (у своих учеников), когда это повышало качество. Есть также и случаи, когда это приводит лишь к переобучению. В любом случае: при решении практической задачи для бизнеса лучше так не делать! Модели становятся совсем неинтерпретируемыми и «неуправляемыми».

Деформация признаков

Очень полезный приём, о котором часто забывают — преобразование (деформация) метапризнакового пространства. Скажем, вместо стандартных метапризнаков (ответов алгоритмов) можно использовать мономы над ними (например, все попарные произведения).

Параметры стекинга

У самого стекинга (а не только алгоритмов, из которых он состоит) есть параметры. Скажем, число фолдов. Как правило выбирают максимальное, при котором он ещё работает (обучается) за приемлемое время. На рис.7 показано качество в модельной задаче от числа фолдов при разном уровне «регуляризационного шума».

Выбор метаалгоритма

Здесь всё просто — он должен оптимизировать заданный функционал качества. От базовых алгоритмов это, вообще говоря, не требуется. Вообще-то, от того, какую композицию Вы будете использовать в ансамбле, сильно зависит качество. Например, в задаче бинарной классификации с функцией ошибки log_loss, если у Вас есть несколько хороших алгоритмов, то сложно придумать стекинг, который их улучшит… Если в качестве метаалгоритма взять гребневую регрессию, то она совсем не годится для log_loss-a, а если логистическую, то обратите внимание на вид Вашего алгоритма: Вы в аргумент сигмоиды «вставляете» линейную комбинацию «почти правильных ответов», вряд ли Вы получите что-то более близкое к правильному ответу…

Связь с другими техниками

Удивительно, но стекинг является обощением практически всего, с чем приходится иметь дело при решении задач. Например, рассмотрим классическую проблему — кодирование категориальных признаков. Если мы для кодирования используем значение целевого вектора, то это эквивалентно тому, что мы получаем метапризнак с помощью байесовского алгоритма, который использует лишь один (кодируемый категориальный) признак. Если мы так закодируем все категориальные признгаки, а потом обучим какой-нибудь алгоритм, то получается, что мы неявно применили стекинг. Ну, а изображение схемы применения стекинга часто похоже на изображение нейронной сети, просто вместо стандартных нейронов используются названия алгоритмов.

Многоуровневый стекинг

Естественное обобщение стекинга — сделать его многоуровневым, т.е. ввести понятие мета-мета-признака (и мета-мета-алгоритма) и т.д. Опять же, лучше воздержаться от этого при решении реальных бизнес-задач, а в спортивном анализе данных так часто делают.

История

Стекинг был предложен Д. Волпертом в 1992 году, хотя, как я уже писал, он постоянно переоткрывается, и, возможно, кто-нибудь использовал уже подобную технику под другим названием раньше. Кстати, Д. Волпертбольше известен как автор серии теорем «No free lunch».

Термин «блендинг» вроде бы ввели в обиход победители конкурса Netflix. Есть постоянная путаница, что называть «стекингом», а что «блендингом». Часто негласно считают, что простые схемы стекинга лучше называть «блендингом».

Удивительно, но стекингу посвящено очень мало научных статей, хотя он порождает очень много теоретических вопросов. Например, как решать задачи машинного обучения в пространстве метапризнаков? Ясно, что в отличие от традиционного признакового пространства здесь все признаки сильно коррелируют друг с другом и с целевым признаком. Это, например, может предъявлять особые требования к регуляризации.

Стекинг часто используют в спортивном анализе данных, в частности, автор с его помощью побеждал в соревнованиии Kaggle WISE 2014 и занимал 3е место в TunedIt JRS 2012.

Геометрия стекинга

Просто приведу пример модельной задачи: линии уровней базовых регрессоров, блендинга и стекинга.

Код

В интернете можно найти разные реализации стекинга, например brew и heamy. Если Вы плотно занимаетесь машинным обучением, то лучше сделать свою. В какой-то момент Вы захотите что-нибудь модифицировать и тогда она Вам пригодится.

Вот ноутбук, в котором есть (достаточно простая) авторская реализация.

Автор: Александр Дьяконов

Ссылка на источник

Источник: m.vk.com

Комментарии: