Что нужно ждать о создании стратегий для торговли на бирже: насколько эффективно машинное обучение

В нашем блоге на Хабре мы публиковали адаптированные переводы материалов из блога The Financial Hacker, посвященные вопросам создания стратегий для торговли на бирже. Ранее мы обсудили поиск рыночных неэффективностей, создание моделей торговых стратегий, и принципы их программирования. Сегодня речь пойдет об использовании подходов машинного обучения для повышения эффективности торговых систем. Первым компьютером, выигравшим мировое первенство по шахматам стал Deep Blue. Это было в 1996 году, и прошло еще двадцать лет, прежде чем другая программа, Alpha Go, сумела победить лучшего игрока в Го. Deep Blue был модель-ориентированной системой с вшитыми правилами игры в шахматы. AplhaGo — это дата-майнинговая система, глубокая нейронная сеть, натренированная с помощью тысяч партий в Го. То есть для того, чтобы сделать шаг от побед над людьми-чемпионами в шахматах, к доминированию над топовыми игроками в Го понадобилась не улучшенная железка, а прорыв в области программного обеспечения.
В текущей статье мы рассмотрим применение подхода дата-майнинга к созданию торговых стратегий. Этот метод не учитывает рыночные механизмы, он просто сканирует ценовые кривые и другие источники данных для поиска предиктивных паттернов. Машинное обучение или «искусственный интеллект» нужны для этого не всегда. Напротив, очень часто, наиболее популярные и прибыльные методы дата-майнинга работают без всяких рюшечек в виде нейронных сетей или поддержки векторных методов.

Принципы машинного обучения

Обучаемому алгоритму «скармливают» образцы данных, обычно каким-то образом выделенных из исторических биржевых цен. Каждый семпл состоит из n переменных x1… xn, которые обычно называют предикторами, функциями, сигналами или, проще, входными данными. Эти предикторы могут быть ценами последних n баров на графике цен или набором значений классических индикаторов, да любыми другими функциями от ценовой кривой (бывают даже случаи, когда в качестве предикторов для нейронной сети используют отдельные пиксели графика цен!). В каждом семпле также обычно содержится некая целевая переменная y, например, результат следующей сделки после анализа семпла или следующее движение цены.

В литературе y часто называют ярлыком или целью (objective). В процессе обучения, алгоритм учится предсказывать целевую y на основе предикторов x1… xn. То, что система «запоминает» в процессе, хранится в структуре данных под названием модель, которая специфична для конкретного алгоритма (тут важно не путать это понятие с финансовой моделью или модель-ориентированной стратегией). Модель машинного обучения может быть функций с правилами предсказаний, записанной с помощью кода на C, сгенерированном процессом обучения. Или это может быть набор связанных весов нейросети:

Обучение: x1… xn, y => модель

Предсказание: x1… xn, модель => y

Предикторы, функции или как вы хотите их назвать, должны содержать информацию, достаточную для генерации предсказаний о значении целевого y с определенной точностью. Также они должны соответствовать двум формальным критериям. Во-первых, все значения предикторов должны находиться в одном диапазоне, например -1… +1 (для большинства алгоритмов на R) или -100… +100 (для алгоритмов на скриптовых языках Zorro или TSSB). Так что перед отправкой данных в систему понадобится их нормализация. Во-вторых, семплы должны быть отбалансированы, то есть равномерно распределены по значениями целевой переменной. То есть у вас должно быть одинаковое число семплов, приводящих к положительному исходу, и проигрышных наборов. Если этим двум требованиям не следовать, то получить хорошие результаты не удастся.

Алгоритмы регрессии генерируют прогнозы о численных значениях, вроде магнитуды или знака следующего ценового движения. Алгоритмы классификации предсказывают количественные классы семплов, например, предшествуют ли они получению прибыли или потере средств. Некоторые алгоритмы, вроде нейронных сетей, деревьев принятия решений или метода опорных векторов могут быть запущены в обоих режимах.

Существуют также алгоритмы, которые могут научиться выделять из семплов класса без необходимости наличия целевого y. Это называется неконтролируемым обучением, в отличие от контролируемого с использованием цели. Где-то между этими двумя методами располагается «подкрепляемое обучение» (reinforcement learning), при котором система тренируется с помощью запуска симуляций с заданными функциями и использует результат в качестве цели. Последователь AlphaGo, система под названием AlphaZero использовала подкрепляемое обучение, играя миллион партий Го сама с собой. В финансах же крайне редко встречаются подобные системы или продукты, использующие неконтролируемое обучение. 99% систем используют контролируемое обучение.

Какие сигналы бы мы не использовали для предикторов в финансах, в большинстве случаев они будут содержать много шума и мало информации, да вдобавок будут нестационарными. Так что предсказания в финансах — одна из сложнейших задач машинного обучения. Более сложные алгоритмы здесь достигают лучших результатов. Выбор предикторов критически важен для успеха. Не обязательно их должно быть много, поскольку это приводит к переобучению и сбоям в работе. Поэтому стратегии дата-майнинга часто применяют заранее отобранный алгоритм, который выделяет небольшое количество предикторов из более широкого пула. Такой предварительный отбор может быть основан на корреляции между предикторами, их значимости, информационной насыщенности или просто успешности/неуспешности использования тестового набора. Практические эксперименты с отбором целей можно найти, например, в блоге Robot Wealth. Ниже — список самых популярных методов дата-майнинга, используемых в сфере финансов.

1. Суп из индикаторов

Большинство торговых систем не основаны на финансовых моделях. Часто трейдерам нужны лишь торговые сигналы, генерируемые определенными техническими индикаторами, которые фильтруются другими индикаторами в комбинации с дополнительными техническими индикаторами. Когда такого трейдера спросить о том, как такая мешанина из индикаторов может приводить к какой-то прибыли, он обычно отвечает что-то вроде: «Поверьте мне, я так руками торгую, и все работает».

И это правда. По крайней мере иногда. Хотя большинство этих систем не пройдут WFA-тест (а некоторые и простое тестирование на исторических данных), удивительно большое количество таких систем в итоге работает и приносит прибыль. Автор блога Financial Hacker занимается в том числе разработкой торговых систем на заказ, и рассказывает историю одного из клиентов, который систематически экспериментировал с техническими индикаторами до тех пор, пока не нашел их комбинацию, работающую для определенных типов активов. Такой метод проб и ошибок — это классический подход к дата-майнингу, для успеха нужен лишь он, удача и много денег на тесты. В результате иногда можно рассчитывать на получение прибыльной системы.

2. Свечные паттерны

Не путать с паттернами японских свечей, которые существуют сотни лет. Современный эквивалент этому подходу — это торговля на основе движений цен. Вы точно также анализируете показатели open, high, low и close для каждой свечи графика. Но теперь вы используете дата-майнинг для анализа свечей ценовой кривой для выделения паттернов, которые могут быть использованы для генерирования прогнозов о направлении движения цены в будущем.

Существуют целые программные пакеты для этой цели. Они ищут паттерны, которые прибыльны с точки зрения заданных пользователем критериев, и используют их для построения функции детектирования паттернов. Выглядеть все это может примерно так:

int detect(double* sig) {   if(sig[1]<sig[2] && sig[4]<sig[0] && sig[0]<sig[5] && sig[5]<sig[3] && sig[10]<sig[11] && sig[11]<sig[7] && sig[7]<sig[8] && sig[8]<sig[9] && sig[9]<sig[6])       return 1;    if(sig[4]<sig[1] && sig[1]<sig[2] && sig[2]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[7]<sig[8] && sig[10]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9])       return 1;   if(sig[1]<sig[4] && eqF(sig[4]-sig[5]) && sig[5]<sig[2] && sig[2]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9])       return 1;   if(sig[1]<sig[4] && sig[4]<sig[5] && sig[5]<sig[2] && sig[2]<sig[0] && sig[0]<sig[3] && sig[7]<sig[8] && sig[10]<sig[11] && sig[11]<sig[9] && sig[9]<sig[6])       return 1;   if(sig[1]<sig[2] && sig[4]<sig[5] && sig[5]<sig[3] && sig[3]<sig[0] && sig[10]<sig[7] && sig[7]<sig[8] && sig[8]<sig[6] && sig[6]<sig[11] && sig[11]<sig[9])       return 1;   ....   return 0; } 

Эта функция на C возвращает 1, когда сигнал подходит одному из паттернов, в противном случае возвращается 0. Длинный код как бы намекает на то, что это не самый быстрый способ поиска паттернов. Лучше использовать подход, при котором функция детектирования не нуждается в экспорте, а может сортировать сигналы по их важности и проводить сортировку. Пример такой системы можно найти по ссылке. Может ли работать «торговля по цене»? Как и в предыдущем случае, этот метод не основан на какой-либо рациональной финансовой модели. При этом, все понимают, что действительно определенные события на рынке, могут влиять на его участников, в результате чего возникают краткосрочные предиктивные паттерны. Но число таких паттернов не может быть большим, если вы изучаете лишь последовательность нескольких последовательных свечей на графике. Затем нужно будет сравнивать результат с данными свечей, которые не находятся рядом, а напротив, случайно выбраны на более длинном временном отрезке. В таком случае вы получите почти неограниченное количество паттернов — и успешно оторветесь от понятий реальности и рациональности. Сложно представить, как можно предсказать будущую цену, на основе каких-то ее значений на прошлой неделе. Несмотря на это, многие трейдеры работают именно в этом направлением.

3. Линейная регрессия

Простой базис множества сложных алгоритмов машинного обучения: предсказать целевую переменную y с помощью линейной комбинации предикторов x1… xn.

Коэффициенты — это и есть модель. Они вычисляются для минимизации суммы квадратичных отклонений между реальными значениями y, тренировочными значениями и предсказанными y по формуле:

Для нормально распределенных семплов, минимизация возможна с помощью матричных операций, так что итерации не требуются. В случае когда n = 1 — с всего одним предикторов x, формула регрессии сокращается до:

— то есть до простой линейной регрессии, а когда n > 1 линейная регрессия будет мультивариантной. Простая линейная регрессия доступна в большинстве торговых платформ, например, индикатор LinReg в TA-Lib. Когда y = цена, а x = время, его можно использовать в качестве альтернативы скользящим средним. В платформе R такая регрессия реализована функцией стандартной поставки lm(..). Также она может быть представлена полиномиальной регрессией. Как и в простейшем случае, здесь используется одна предиктивная переменная x, но также ее квадрат и последующие степени, так что xn == xn: Если n = 2 или n = 3, полиномиальная регрессия часто используется для предсказания следующего среднего значения цены от сглаженных цен последних баров. Для полиномиальной регрессии может быть использована функция polyfit фреймворков MatLab, R, Zorro и многих других платформ.

4. Перцептрон

Часто его называют нейросетью с всего одним нейроном. По факту же перцептрон — это функция регрессии, как описанные выше, но с двоичным результатом, в результате чего его называют логистической регрессией. Хотя вообще-то это не регрессия, а алгоритм классификации. К примеру, функция advise(PERCEPTRON, …) фреймворка Zorro генерирует код на C, которые возвращает 100 или -100 в зависимости от того, является ли предсказанный результат пороговым или нет:

int predict(double* sig) {   if(-27.99*sig[0] + 1.24*sig[1] - 3.54*sig[2] > -21.50)     return 100;   else     return -100; }

Как нетрудно заметить, массив sig эквивалентен функциям xn в формуле регрессии, а цифровыми факторами являются коэффициенты an.

5. Нейронные сети

Линейная или логистическия регрессия могут решать только линейные проблемы. При этом задачи трейдинга часто в эту категорию не укладываются. Знаменитый пример — предсказание вывода простой функции XOR. Сюда же попадает и предсказание прибыли от сделок. Искусственная нейросеть (artificial neural network, ANN) может решать нелинейные проблемы. Это набор перцептронов, которые соединены в массив различных уровней. Каждый перцептрон — это нейрон сети. Его выходные данные становятся входными для других нейронов следующего уровня:

Как и перцептрон, нейросеть обучается, определяя коэффициенты, которые минимизируют ошибку между предсказанием и целью в семпле. Для этого требуется процесс аппроксимации, обычно с обратным распространением ошибки от выходных данных к входным с попутной оптимизацией весов. Этот процесс накладывает два ограничения. Во-первых, вывод нейронов должен представлять собой постоянно дифференцируемую функцию вместо простого порога для перцептрона. Во-вторых, сеть должна быть не очень глубокой — наличие большого количества скрытых уровней нейронов между входными и выходными данными только вредит. Это второе ограничение лимитирует сложность проблем, которую может решить стандартная нейронная сеть. При использовании нейронных сетей для предсказания сделок, у вас будет множество параметров, с которыми можно манипулировать, что при неаккуратной работе может вылиться в появление предубеждений выбора (selection bias):

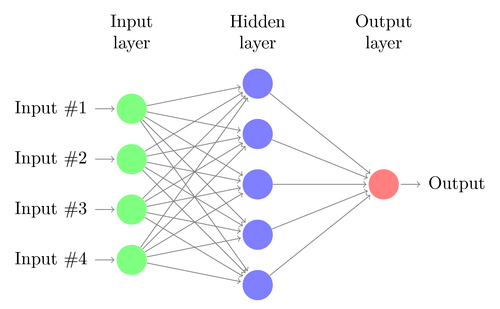
• число скрытых уровней;
• число нейронов в каждом скрытом уровне;
• количество циклов обратного распространения — эпох;
• степень обучения, ширина шага эпохи;
• моментум, фактор инерции для адаптации весов;
• функция активации.

Функция активации эмулирует порог перцептрона. Для обратного распространения понадобится постоянно дифференцируемая функция, которая генерирует мягкий шаг для определенного значения x. Обычно для этого используются функции sigmoid, tanh или softmax function. Иногда используется линейная функция, которая возвращает взвешенную сумму всех входных данных. В этом случае сеть может быть использована для регрессии, предсказания численных значений вместо бинарного вывода.

Нейросети входят в стандартную поставку пакета R (например, nnet — сеть с одним скрытым уровнем), а также во многие другие пакеты (вроде RSNNS и FCNN4R).

6. Глубокое обучение

Методы глубокого обучения используют нейросети с большим количеством скрытых уровней и тысячами нейронов, которые невозможно эффективно обучить с помощью простого обратного распространения. В последние годы для обучения таких больших сетей приобрели популярность несколько методов. Они обычно подразумевают предварительное обучение скрытых уровней нейронов для повышения эффективности основного обучения.

Ограниченная машина Больцмана (Restricted Boltzmann Machine, RBM) — это неконтролируемый алгоритм классификации со специальной сетевой структурой, в которой нет связей между скрытыми нейронами. Автокодировщик Sparse (SAE) использует обычную сетевую структуру, но предварительно обучает скрытые уровни определенным способом, воспроизводя входные сигналы на выходных уровня с как можно меньшим количеством активных соединений. Эти методы позволяют реализовывать очень сложные сети для решения очень сложных задач обучения. Например, задачу победить лучшего человека, играющего в Го. Сети глубокого обучения входят в пакеты deepnet и darch для R. В deepnet входит автокодировщик, а в darch — машина Больцмана. Ниже — пример кода, использующего deepnet с тремя скрытыми уровнями для обработки торговых сигналов через функцию neural() фреймворка Zorro:

library('deepnet', quietly = T)  library('caret', quietly = T)  # called by Zorro for training neural.train = function(model,XY)  {   XY <- as.matrix(XY)   X <- XY[,-ncol(XY)] # predictors   Y <- XY[,ncol(XY)]  # target   Y <- ifelse(Y > 0,1,0) # convert -1..1 to 0..1   Models[[model]] <<- sae.dnn.train(X,Y,       hidden = c(50,100,50),        activationfun = "tanh",        learningrate = 0.5,        momentum = 0.5,        learningrate_scale = 1.0,        output = "sigm",        sae_output = "linear",        numepochs = 100,        batchsize = 100,       hidden_dropout = 0,        visible_dropout = 0) }  # called by Zorro for prediction neural.predict = function(model,X)  {   if(is.vector(X)) X <- t(X) # transpose horizontal vector   return(nn.predict(Models[[model]],X)) }  # called by Zorro for saving the models neural.save = function(name) {   save(Models,file=name) # save trained models }  # called by Zorro for initialization neural.init = function() {   set.seed(365)   Models <<- vector("list") }  # quick OOS test for experimenting with the settings Test = function()  {   neural.init()   XY <<- read.csv('C:/Project/Zorro/Data/signals0.csv',header = F)   splits <- nrow(XY)*0.8   XY.tr <<- head(XY,splits) # training set   XY.ts <<- tail(XY,-splits) # test set   neural.train(1,XY.tr)   X <<- XY.ts[,-ncol(XY.ts)]   Y <<- XY.ts[,ncol(XY.ts)]   Y.ob <<- ifelse(Y > 0,1,0)   Y <<- neural.predict(1,X)   Y.pr <<- ifelse(Y > 0.5,1,0)   confusionMatrix(Y.pr,Y.ob) # display prediction accuracy }

7. Опорные векторы

Как и в случае нейросетей, метод опорных векторов — еще одно расширение линейной регрессии. Если взглянуть на формулу регрессии еще раз:

То можно интерпретировать функции xn в качестве координат n-размерного пространства. Установка целевой переменной y в фиксированное значение определит плоскость в этом пространстве – оно будет называться гиперплоскостью, поскольку по факту в ней будет два (даже n-1) размера. Гиперплоскость отделяет семплы с y > 0 от тех, где y < 0. Коэффициенты an можно вычислить как путь, разделяющий плоскость от ближайших семплов — ее опорных векторов, отсюда и название алгоритма. Таким образом мы получаем бинарный классификатор с оптимальным разделением выигрышных и проигрышных семплов.

Проблема: обычно эти семплы нельзя разделить линейно – они случайно группируются в пространстве функций. Между выигрышными и проигрышными вариантами нельзя провести гладкую плоскость, если бы это можно было сделать, то для ее вычисления можно было бы использовать более простые методы вроде линейного анализа дискриминанта. Но в общем случае можно использовать трюк: добавить больше размеров в пространство. В таком случае алгоритм опорных векторов сможет сгенерировать больше параметров с ядерной функцией, комбинирующей два любых предиктора — по аналогии перехода от простой регрессии к полиномиальной. Чем больше размеров вы добавляете, тем проще разделить семплы гиперплоскостью. Затем ее можно преобразовать обратно к оригинальному n-размерному пространству.

Как и нейросети, опорные векторы могут быть использованы не только для классификации, но и для регрессии. Также они предлагают ряд параметров для оптимизации и возможного переобучения:

• Функция ядра — обычно используется RBF-ядро (радиальная базисная функция, симметричное ядро), но можно выбрать и другие ядра, например сигмоид, полиномиальное и линейное.
• Гамма — ширина ядра RBF.
• Параметр стоимости C, «штраф» за неверные классификации обучающих семплов.

Часто используется библиотека libsvm, которая доступна в пакете e1071 для R.

8. Алгоритм k-ближайших соседей

В сравнении с тяжелыми ANN и SVM, это простой и приятный алгоритм с уникальным свойством: его не нужно обучать. Семплы и будут моделью. Этот алгоритм можно использовать для торговой системы, которая постоянно обучается с помощью добавления новых семплов. Этот алгоритм вычисляет дистанции в пространстве функций от текущего значения к k-ближайшим семплам. Дистанция в n-размерном пространстве между двумя наборами (x1… xn) и (y1… yn) вычисляется по формуле:

Алгоритм просто предсказывает цель от среднего k целевых переменных ближайших семплов, взвешенных по их обратным расстояниям. Его можно использовать как для классификации, так и для регрессии. Для предсказания ближайших соседей можно вызвать функцию knn в R или самостоятельно написать код на C для этой цели.

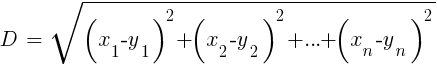
9. K-средние

Это алгоритм аппроксимации для неконтролируемой классификации. Он чем-то похож на предыдущий алгоритм. Для классификации семплов алгоритм сначала размещает в пространстве функций k случайных точек. Затем он присваивает какой-то из этих точек все семплы с наименьшим расстоянием до нее. Затем точка сдвигает к среднему от этих ближайших значений. Это генерирует новые привязки семплов, поскольку какие-то из них теперь окажутся ближе к другим точкам. Процесс повторяется до тех пор, пока перепривязка в результате сдвига точек не прекратится, то есть до тех пор, пока каждая точка не окажется средней для ближайших семплов. Теперь у нас есть k классов семплов, каждый расположенный по соседству от какой-то k-точки.

Этот простой алгоритм может приносить удивительно хорошие результаты. В R для его реализации используется функция kmeans, пример алгоритма можно найти по ссылке.

10. Наивный Байес

Этот алгоритм использует Байесовскую теорему классификации семплов нечисловых функций (событий), вроде упомянутых выше свечных паттернов. Предположим, что событие X (например, параметр Open предыдущего бара ниже параметра Open текущего бара) появляется в 80% выигрышных семплов. Тогда какова будет вероятность выигрышности семпла при наличии в нем события X? Это не 0,8 как можно подумать. Эта вероятность вычисляется по формуле:

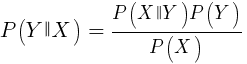P(Y|X) — это вероятность того, что событие Y (получение прибыли) возникнет во всех семплах, содержащих событие X (в нашем примере Open(1) < Open(0)). В соответствии с формулой, она равняется вероятности возникновении события X во всех выигрышных семплах (в нашем случае 0,8), умноженной на вероятность Y во всех семплах (примерно 0,5 если следовать советам по балансированию семплам) и разделенной на вероятность появления X во всех семплах.

Если мы наивны и предполагаем, что все события X независимы друг от друга, то можно подсчитать общую вероятность того, что семпл окажется выигрышным с помощью простого перемножения вероятностей P(X|winning) для каждого события X. Тогда мы придем к следующей формуле:

С фактором масштабирования s. Чтобы формула заработала, функции должны быть выбраны таким образом, чтобы они были максимально независимыми. Это будет препятствием для использования наивного Байеса для трейдинга. К примеру, два события Close(1) < Close(0) и Open(1) < Open(0) с большой вероятностью не независимы друг от друга. Числовые предикторы можно конвертировать в события, разделив число на отдельные диапазоны. Наивный Байес доступен в пакете e1071 для R.

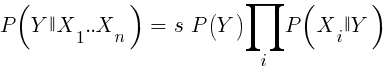
11. Деревья решений и регрессий

Такие деревья предсказывают результат численных значений, основанных на цепочке принятия решений в формате да/нет в структуре ветвей дерева. Каждое решение представляет собой наличие или отсутствие событий (в случае не-числовых значений) или сравнения значений с фиксированным порогом. Типичная древесная функция, сгенерированная, например, фреймворком Zorro, выглядит так:

int tree(double* sig) {   if(sig[1] <= 12.938) {     if(sig[0] <= 0.953) return -70;     else {       if(sig[2] <= 43) return 25;       else {         if(sig[3] <= 0.962) return -67;         else return 15;       }     }   }   else {     if(sig[3] <= 0.732) return -71;     else {       if(sig[1] > 30.61) return 27;       else {           if(sig[2] > 46) return 80;           else return -62;       }     }   } }

Как такое дерево получается из набора семплов? Для этого может быть несколько методов, включая информационную энтропию Шеннона. Деревья принятия решений могут довольно широко применяться. Например, они подходят для генерирования предсказаний, более точных, чем удается достичь с помощью нейросетей или опорных векторов. Однако это не универсальное решение. Наиболее известный алгоритм такого типа это C5.0, доступный в пакете C50 для R.
Для еще большего повышения качества предсказаний, можно использовать наборы деревьев — они называются случайным лесом. Этот алгоритм доступен в пакетах R под названием randomForest, ranger и Rborist.

Заключение

Существует множество методов дата-майнинга и машинного обучения. Критичный вопрос здесь заключается в следующем: что лучше, стратегии, основанные на моделях или на машинном обучении? Нет сомнений в том, что у машинного обучения есть ряд плюсов. Например, вам не нужно заботиться микроструктуре рынка, экономике, учитывать философию участников рынка или другие подобные вещи. Можно сконцентрироваться на чистой математике. Машинное обучение куда более элегантный и привлекательный способ создания торговых систем. На его стороне все плюсы, кроме одного — помимо рассказов на форумов трейдеров, успехи этого метода в реальной торговле отследить проблематично.

Чуть ли не каждую неделю публикуются новые статьи о трейдинге с помощью машинного обучения. Такие материалы следует воспринимать с изрядной долей скепсиса. Авторы некоторых работ заявляют о фантастических показателях выигрышности в 70%, 80% или даже 85%. При этом мало кто говорит, что потерять деньги можно даже в случае выигрышности предсказаний. Точность в 85% обычно транслируется в показатель прибыльности выше 5 — если бы все было так просто, то создатели такой системы уже бы стали миллиардерами. Однако, почему-то, воспроизвести такие же результаты, просто повторяя описанные в статьях методы, не получается.

По сравнению с системами, основанными на моделях, реальных успешных систем машинного обучения очень мало. Например, их редко используют успешные хедж-фонды. Возможно в будущем, когда вычислительные мощности станут еще более доступны, что-то и поменяется, но пока алгоритмы глубокого обучения остаются больше интересным хобби для гиков, нежели реальным инструментом заработка на бирже.

Другие материалы по теме финансов и фондового рынка от ITI Capital:

• Аналитика и обзоры рынка
• Назад в будущее: проверка работоспособности торгового робота с помощью исторических данных
• Событийно-ориентированный бэктестинг на Python шаг за шагом (Часть 1, Часть 2, Часть 3, Часть 4, Часть 5)