Анализ данных — основы и терминология

В этой статье я бы хотел обсудить базовые принципы построения практического проекта по (т. н. «интеллектуальному») анализу данных, а также зафиксировать необходимую терминологию, в том числе русскоязычную.

Согласно википедии,

Анализ данных — это область математики и информатики, занимающаяся построением и исследованием наиболее общих математических методов и вычислительных алгоритмов извлечения знаний из экспериментальных (в широком смысле) данных; процесс исследования, фильтрации, преобразования и моделирования данных с целью извлечения полезной информации и принятия решений.

Говоря чуть более простым языком, я бы предложил понимать под анализом данных совокупность методов и приложений, связанных с алгоритмами обработки данных и не имеющих четко зафиксированного ответа на каждый входящий объект. Это будет отличать их от классических алгоритмов, например реализующих сортировку или словарь. От конкретной реализации классического алгоритма зависит время его выполнения и объем занимаемой памяти, но ожидаемый результат его применения строго зафиксирован. В противоположность этому мы ожидаем от нейросети, распознающей цифры, ответа 8 при входящей картинке, изображающей рукописную восьмерку, но не можем требовать этого результата. Более того, любая (в разумном смысле этого слова) нейросеть будет иногда ошибаться на тех или иных вариантах корректных входных данных. Будем называть такую постановку задачи и применяющиеся при ее решении методы и алгоритмы недетерминистическими (или нечеткими) в отличии от классических (детерминистических, четких).

Алгоритмы и эвристики

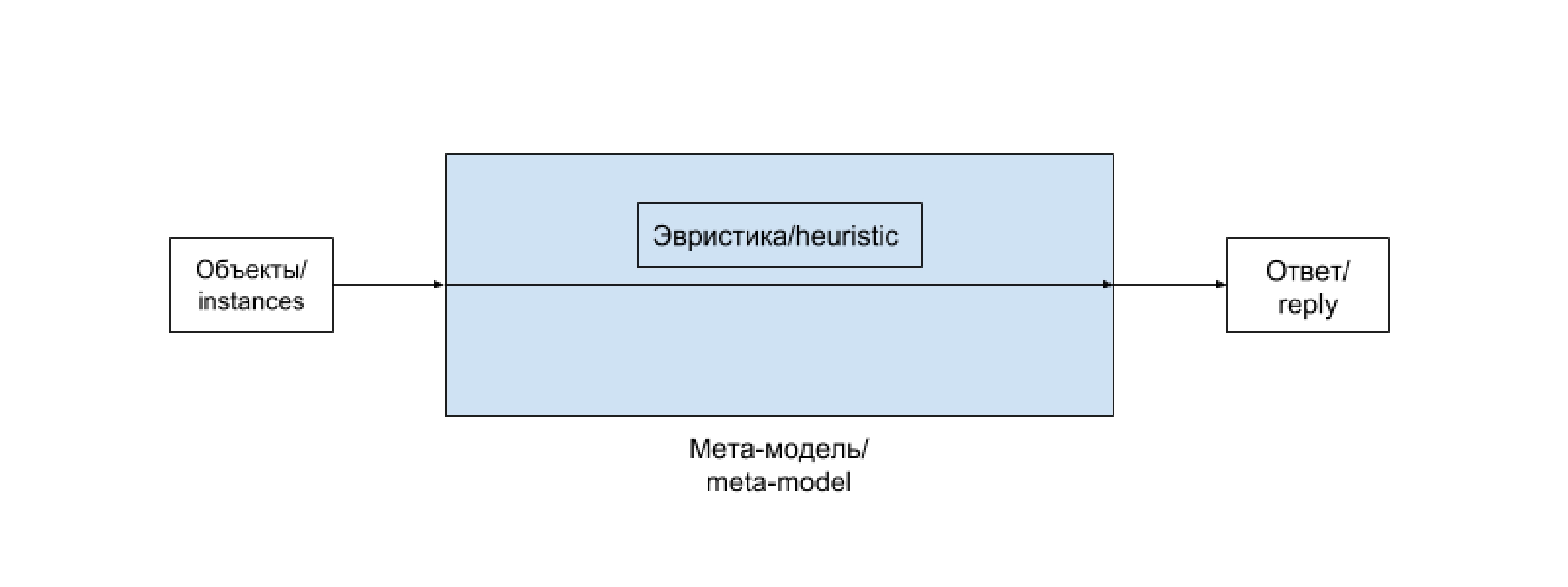
Описанную задачу распознавания цифр можно решать пытаясь самостоятельно подобрать функцию, реализующую соответствующее отображение. Получится, скорее всего, не очень быстро и не очень хорошо. С другой стороны, можно прибегнуть к методам машинного обучения, то есть воспользоваться вручную размеченной выборкой (или, в других случаях, теми или иными историческими данными) для автоматического подбора решающей функции. Таким образом, здесь и далее (обобщенным) алгоритмом машинного обучения я буду называть алгоритм, так или иначе на основе данных формирующий недетерминистический алгоритм, решающий ту или иную задачу. (Недетерминистичность полученного алгоритма нужна для того, чтобы под определение не подпадал справочник, использующий предварительно подгруженные данные или внешний API).

Таким образом, машинное обучение является наиболее распространенным и мощным (но, тем не менее, не единственным) методом анализа данных. К сожалению, алгоритмов машинного обучения, хорошо обрабатывающих данные более или менее произвольной природы люди пока не изобрели и поэтому специалисту приходится самостоятельно заниматься предобработкой данных для приведения их в пригодный для применения алгоритма вид. В большинстве случаев такая предобработка называется фичеселектом (англ. feature selection) или препроцессингом. Дело в том, что большинство алгоритмов машинного обучения принимают на вход наборы чисел фиксированной длины (для математиков — точки в $$). Однако сейчас также широко используются разнообразные алгоритмы на основе нейронных сетей, которые умеют принимать на вход не только наборы чисел, но и объекты, имеющие некоторые дополнительные, главным образом геометрические, свойства, такие как изображения (алгоритм учитывает не только значения пикселей, но и их взаимное расположение), аудио, видео и тексты. Тем не менее, некоторая предобработка как правило происходит и в этих случаях, так что можно считать, что для них фичеселект заменяется подбором удачного препроцессинга.

Алгоритмом машинного обучения с учителем (в узком смысле этого слова) можно назвать алгоритм (для математиков — отображение), который берет на вход набор точек в $$ (еще называются примерами или samples) $$ и меток (значений, которые мы пытаемся предсказать) $$, а на выходе дает алгоритм (=функцию) $$, уже сопоставляющий конкретное значение $$ любому входу $$, принадлежащему пространству примеров. Например, в случае упомянутой выше нейросети, распознающей цифры, с помощью специальной процедуры на основе обучающей выборки устанавливаются значения, соответствующие связям между нейронами, и с их помощью на этапе применения вычисляется то или иное предсказание для каждого нового примера. Кстати, совокупность примеров и меток называется обучающей выборкой.

Список эффективных алгоритмов машинного обучения с учителем (в узком смысле) строго ограничен и почти не пополняется несмотря на активные исследования в этой области. Однако для правильного применения этих алгоритмов требуется опыт и подготовка. Вопросы эффективного сведения практической задачи к задаче анализа данных, подбора списка фичей или препроцессинга, модели и ее параметров, а также грамотного внедрения непросты и сами по себе, не говоря уже о работе над ними в совокупности.

Общая схема решения задачи анализа данных при использовании метода машинного обучения выглядит таким образом:

Цепочку «препроцессинг — модель машинного обучения — постпроцессинг» удобно выделять в единую сущность. Часто такая цепочка остается неизменной и лишь регулярно дообучается на новопоступивших данных. В некоторых случаях, особенно на ранних этапах развития проекта, ее содержимое заменяется более или менее сложной эвристикой, не зависящей напрямую от данных. Бывают и более хитрые случаи. Заведем для такой цепочки (и возможных ее вариантов) отдельный термин и будем называть мета-моделью (meta-model). В случае эвристики она редуцируется до следующей схемы:

Эвристика — это просто вручную подобранная функция, не использующая продвинутых методов, и, как правило, не дающая хорошего результата, но приемлемая в определенных случаях, например на ранних стадиях развития проекта.

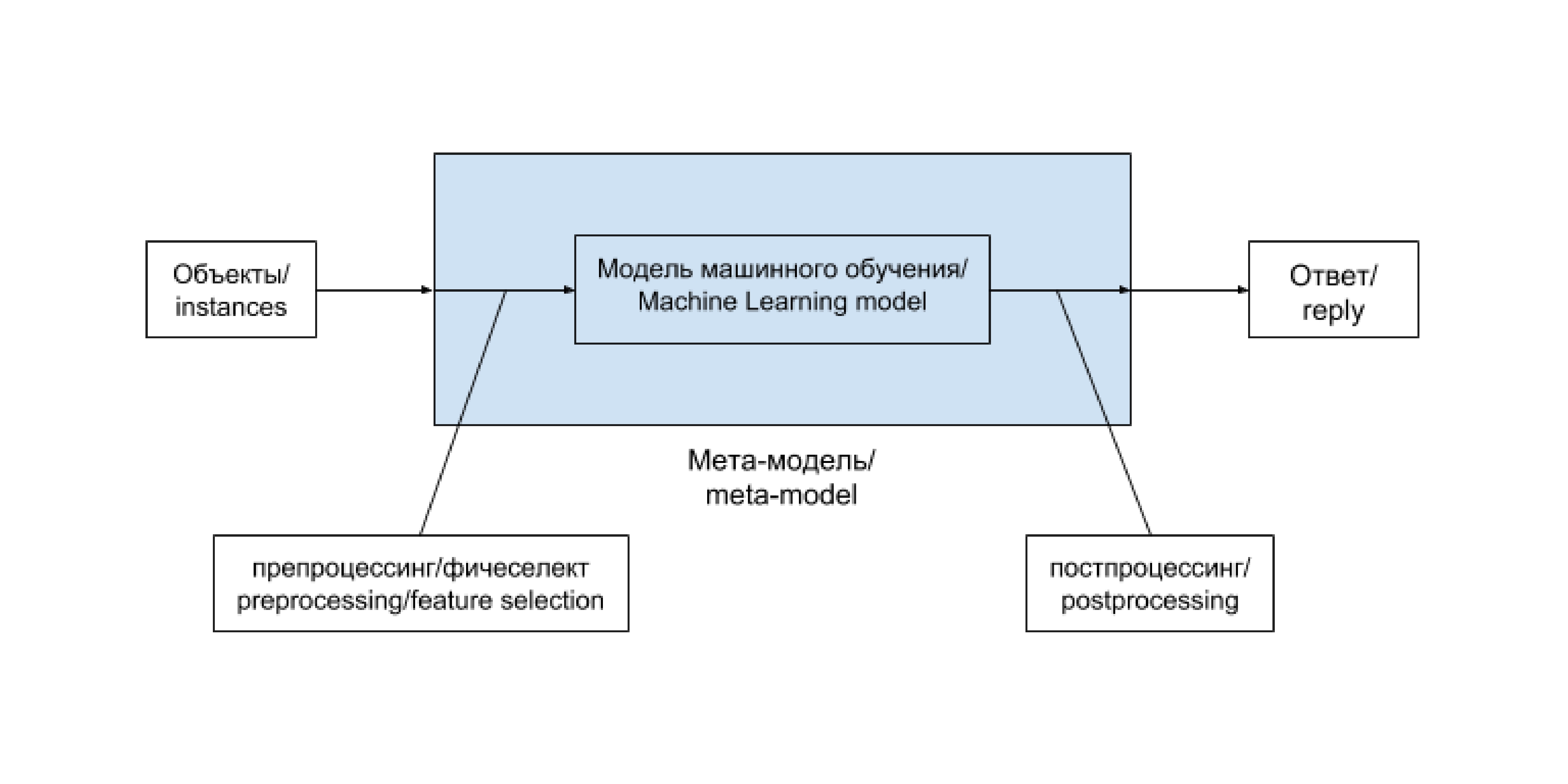
Задачи машинного обучения с учителем

В зависимости от постановки, задачи машинного обучения делят на задачи классификации, регрессии и логистической регрессии.

Классификация — постановка задачи при которой требуется определить, какому классу из некоторого четко заданного списка относится входящий объект. Типичным и популярным примером является уже упоминавшееся выше распознавание цифр, в ней каждому изображению нужно сопоставить один из 10 классов, соответствующий изображенной цифре.

Регрессия — постановка задачи, при которой требуется предсказать некоторую количественную характеристику объекта, например цену или возраст.

Логистическая регрессия сочетает свойства перечисленных выше двух постановок задач. В ней задаются совершившиеся события на объектах, а требуется предсказать их вероятности на новых объектах. Типичным примером такой задачи является задача предсказания вероятности перехода пользователя по рекомендательной ссылке или рекламному объявлению.

Выбор метрики и валидационная процедура

Метрика качества предсказания (нечеткого) алгоритма — это способ оценить качество его работы, сравнить результат его применения с действительным ответом. Более математично — это функция, берущая на вход список предсказаний $$ и список случившихся ответов $$, а возвращающая число соответствующее качеству предсказания. Например в случае задачи классификации самым простым и популярным вариантом является количество несовпадений $$, а в случае задачи регрессии — среднеквадратичное отклонение $$. Однако в ряде случаев из практических соображений необходимо использовать менее стандартные метрики качества.

Прежде чем внедрять алгоритм в работающий и взаимодействующий с реальными пользователями продукт (или передавать его заказчику), хорошо бы оценить, насколько хорошо этот алгоритм работает. Для этого используется следующий механизм, называемый валидационной процедурой. Имеющаяся в распоряжении размеченная выборка разделяется на две части — обучающую и валидационную. Обучение алгоритма происходит на обучающей выборке, а оценка его качества (или валидация) — на валидационной. В том случае, если мы пока не используем алгоритм машинного обучения, а подбираем эвристику, можно считать, что вся размеченная выборка, на которой мы оцениваем качество работы алгоритма является валидационной, а обучающая выборка пуста — состоит из 0 элементов.

Типичный цикл развития проекта

В самых общих чертах цикл развития проекта по анализу данных выглядит следующим образом.

1. Изучение постановки задачи, возможных источников данных.
2. Переформулировка на математическом языке, выбор метрик качества предсказания.
3. Написание пайплайна для обучения и (хотя бы тестового) использования в реальном окружении.
4. Написание решающей задачу эвристики или несложного алгоритма машинного обучения.
5. По необходимости улучшение качества работы алгоритма, возможно уточнение метрик, привлечение дополнительных данных.

Заключение

На этом пока все, следующий раз мы обсудим какие конкретно алгоритмы применяются для решения задач классификации, регрессии и логистической регрессии, а о том, как сделать базовое исследование задачи и подготовить его результат для использования прикладным программистом уже можно почитать здесь. P.S. В соседнем топике я немножко поспорил с людьми, придерживающимися более академичной точки зрения на вопросы машинного обучения, чем моя. Что несколько негативно сказалось на моей хаброкарме. Так что если вы хотели бы ускорить появление следующей статьи и обладаете соответствующими полномочиями — поплюсуйте меня немножко, это поможет мне написать и выложить продолжение более оперативно. Спасибо.