Случайные эволюционные стратегии в машинном обучении

Нейронные сети учатся совсем не так как люди. Оптимизация нейронной сети — на самом деле градиентный спуск по некоторой функции потерь $$, где переменными являются веса слоёв $$. Это очень мощный подход к подстройке системы, который применяется также в физике, экономике и многих других областях. На данный момент предложено немало конкретных методов градиентного спуска, но все они предполагают, что градиент $$ хорошо себя ведёт: нет обрывов, где он скачкообразно возрастает, или плато, где он обращается в ноль. С первой проблемой можно разобраться при помощи gradient clipping, но вторая заставляет тщательно подумать. Кусочно-линейную или дискретную функцию нетривиально ограничить более приятной функцией

• во многих областях reinforcement learning (далее RL)
• в VAE с дискретными латентными переменными
• в GAN с дискретными генераторами

Как поступать в таких ситуациях?

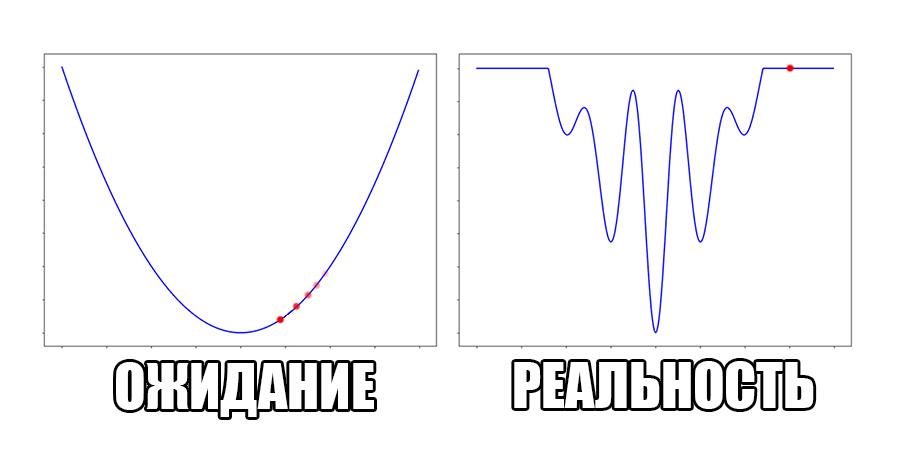
Под катом много формул и гифок.

Около пяти лет назад начали появляться статьи, исследующие другой подход к обучению: вместо сглаживания целевой функции, давайте в таких случаях приближённо считать градиент. Определённым образом сэмплируя значения $$, можно предположить, куда следует двигаться, даже если в текущей точке производная ровно ноль. Не то чтобы подходы с сэмплированием были особо новы — Монте-Карло уже много времени дружит с нейронными сетями — но недавно были получены новые интересные результаты.

За основу этой статьи были взяты записи в блоге Ferenc Husz?r.

Random Evolution Strategy (ES)

Начнём с самого простого подхода, который вновь обрёл популярность после статьи OpenAI в 2017. Замечу, что у эволюционных стратегий не слишком удачное имя, связанное с развитием этого семейства алгоритмов. С генетическими алгоритмами ES связаны очень отдалённо — лишь случайным изменением параметров. Гораздо продуктивнее думать о ES, как о методе оценки градиента при помощи сэмплирования. Мы сэмплируем из нормального распределения $$ несколько векторов пертурбаций $$, берём матожидание от получившихся значений целевой функции, и считаем, что

$$

Идея довольно проста. При стандартном градиентном спуске мы на каждом шаге смотрим наклон поверхности, на которой находимся, и двигаемся в сторону наибольшего уклона. В ES мы «обстреливаем» близлежащую окрестность точками, куда мы можем предположительно двинуться, и перемещаемся в сторону, куда попало больше всего точек с наибольшей разницей высот (причём, чем дальше точка, тем больший ей придаётся вес).

Доказательство тоже несложное. Предположим, что на самом деле функцию потерь можно разложить в ряд Тейлора в $$:

$$

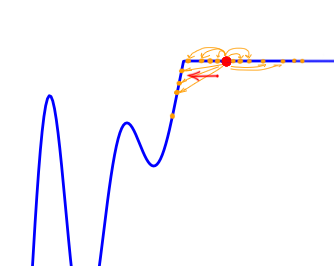
Умножим обе стороны на $$:

$$

Отбросим $$ и возьмём матожидание от обоих сторон:

$$

Но нормальное распределение симметрично: $$, $$, $$:

$$

Поделим на $$ и получим исходное утверждение.

В случае кусочно-ступенчатой функции получившаяся оценка $$ будет представлять градиент сглаженной функции без надобности вычислять конкретные значения этой функции в каждой точке; в статье даны более строгие утверждения. Также в случае, когда функция потерь зависит от дискретных параметров $$ (т.е. $$), можно показать что оценка остаётся справедливой, так как при доказательстве можно поменять местами порядок взятия матожидания

$$

Что часто невозможно для обычного SGD.

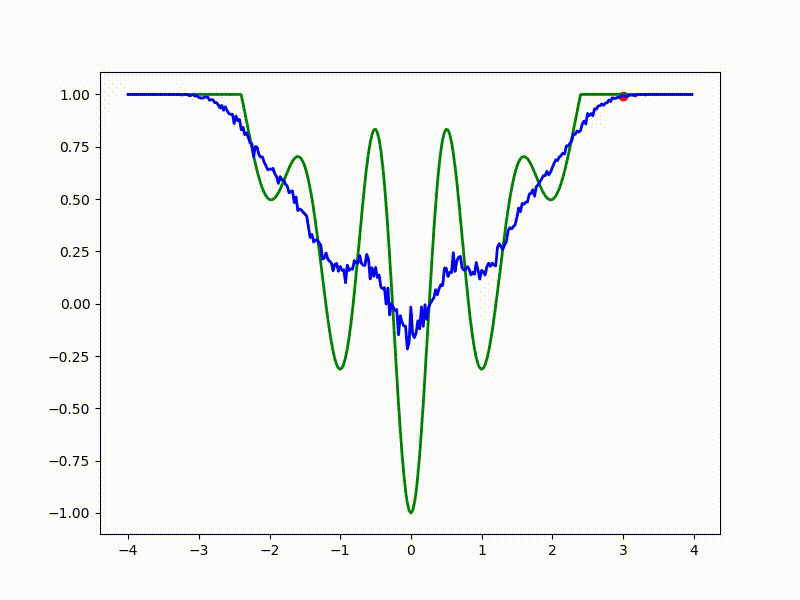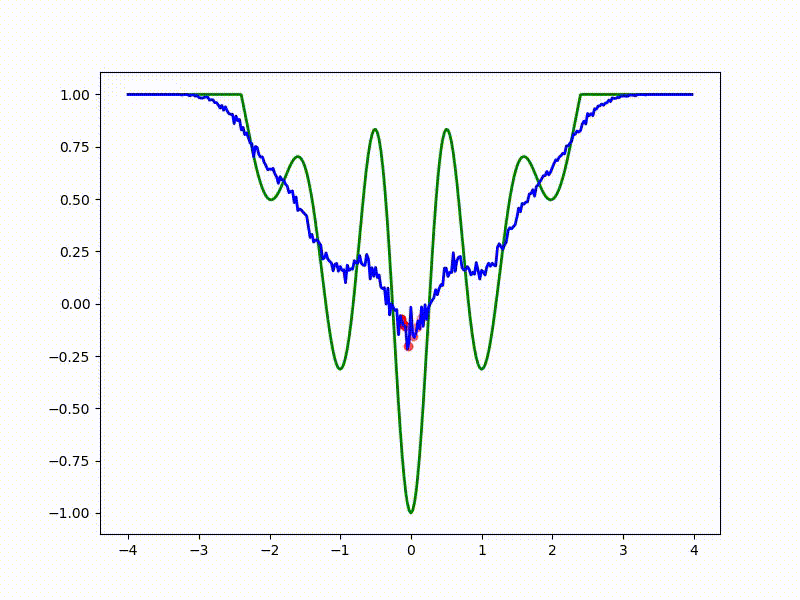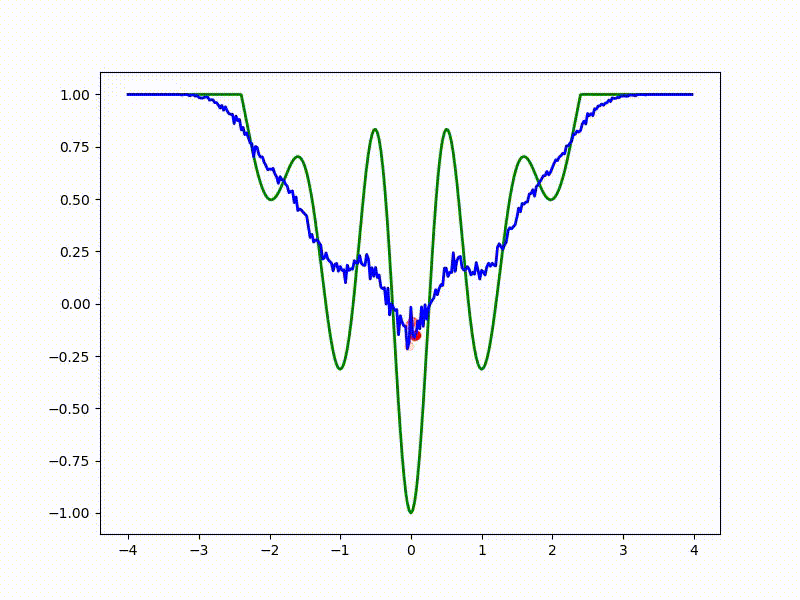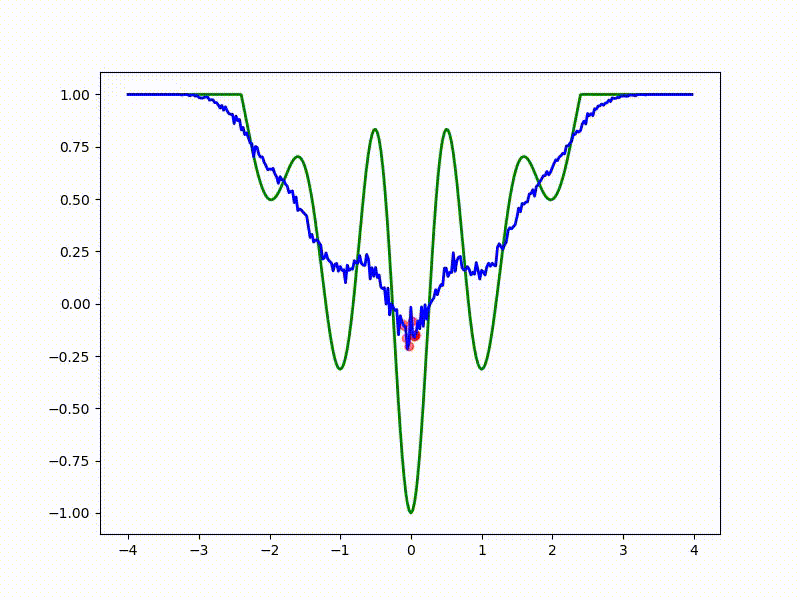
Посмотрим на функцию, сглаженную при помощи сэмплирования из $$. Ещё раз: в действительности нет смысла считать $$, нам нужны лишь производные. Однако, подобные визуализации помогают понять, по какому ландшафту реально производится градиентный спуск. Итак, зелёный график — исходная функция, синий — как она выглядит для алгоритма оптимизации после оценки градиента сэмплированием:

$$:

$$:

$$:

Чем больше сигма распределения, тем меньше проявляет себя локальная структура функции. При слишком большом размахе сэмплирования алгоритму оптимизации не видны узкие минимумы и ложбины, по которым можно перейти из одного хорошего состояния в другое. При слишком малом — градиентный спуск может так и не стартовать, если точка инициализации была выбрана неудачно.

Больше графиков:

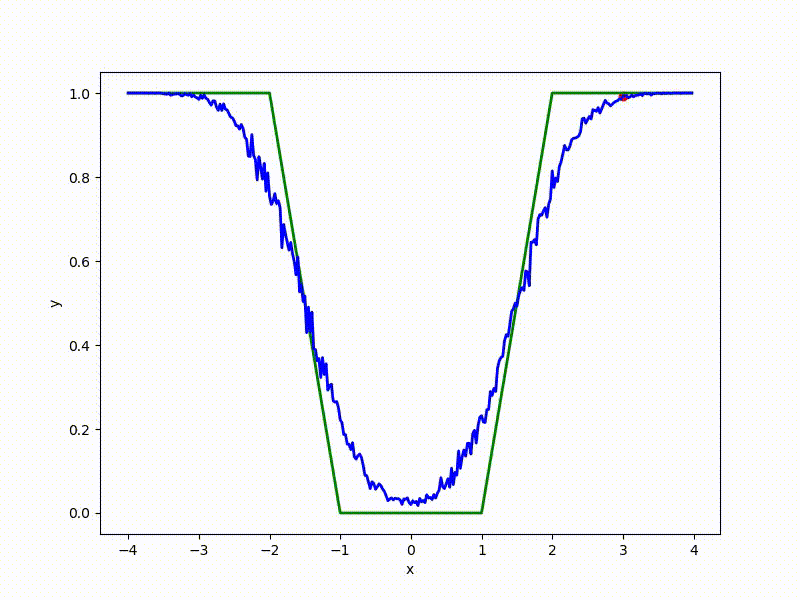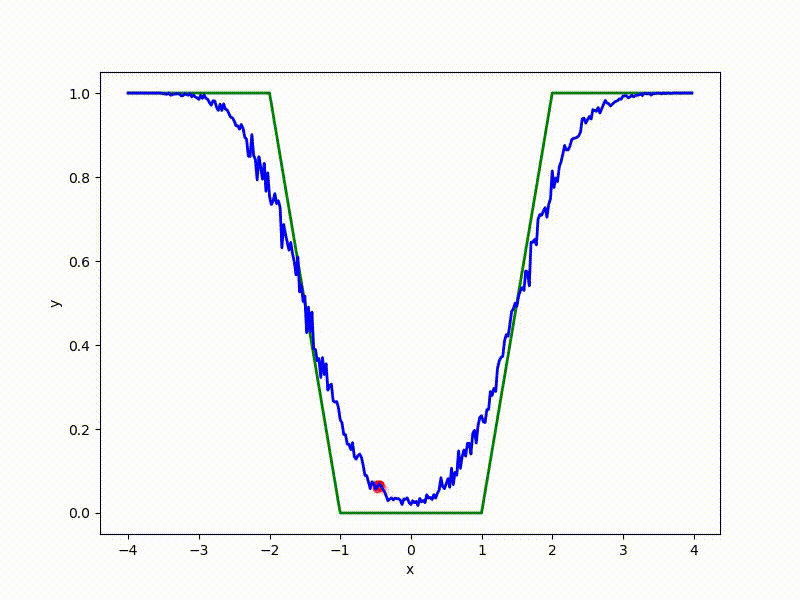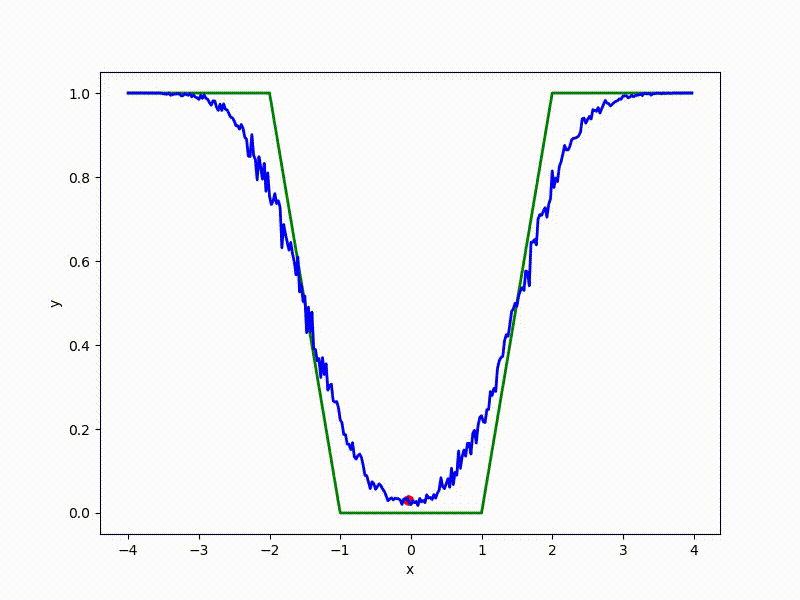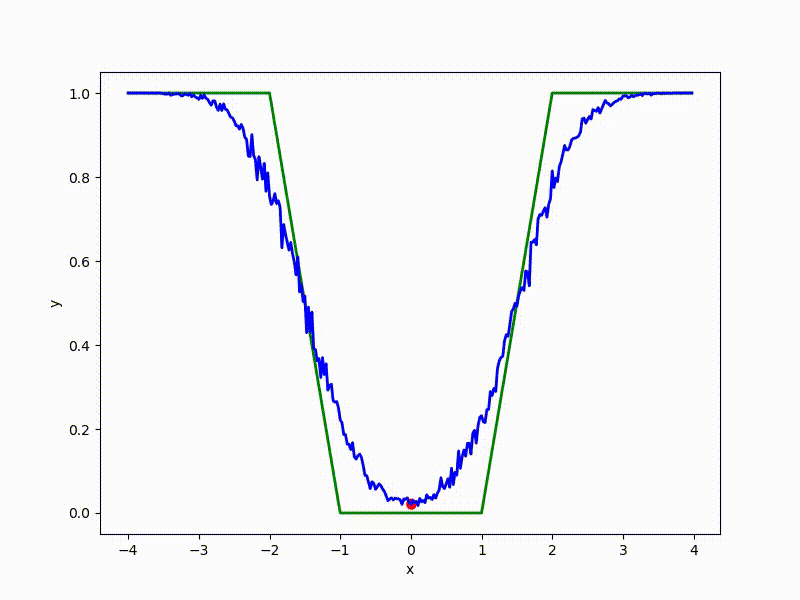
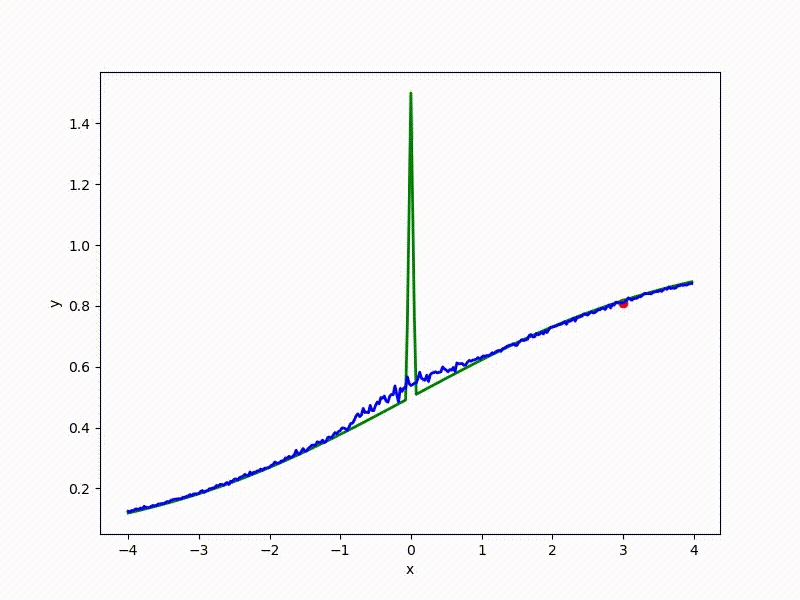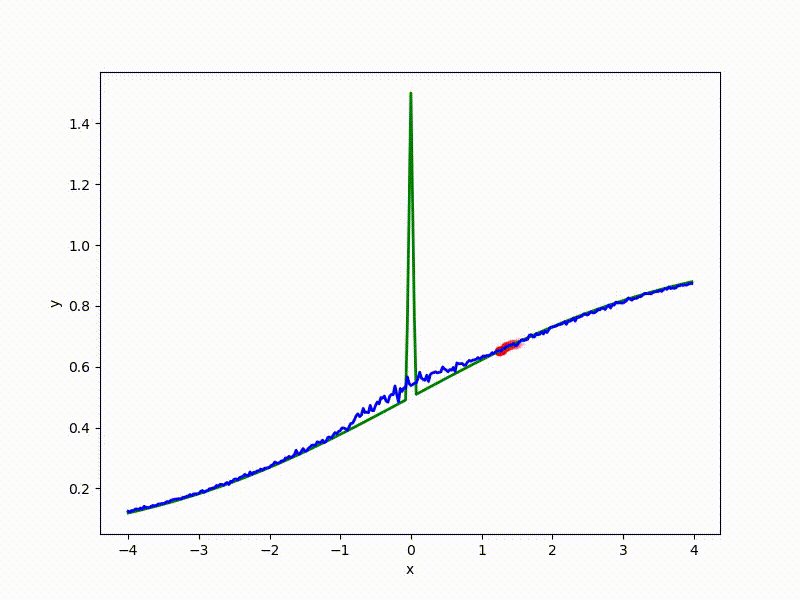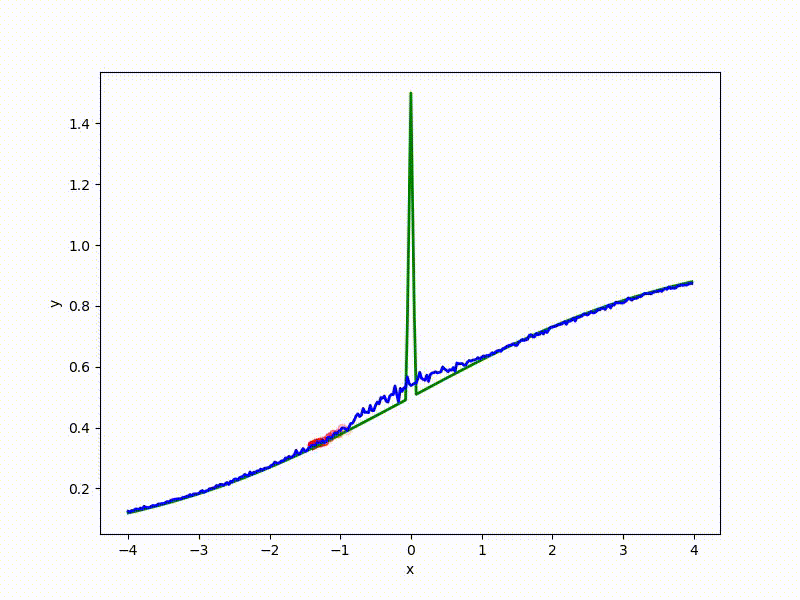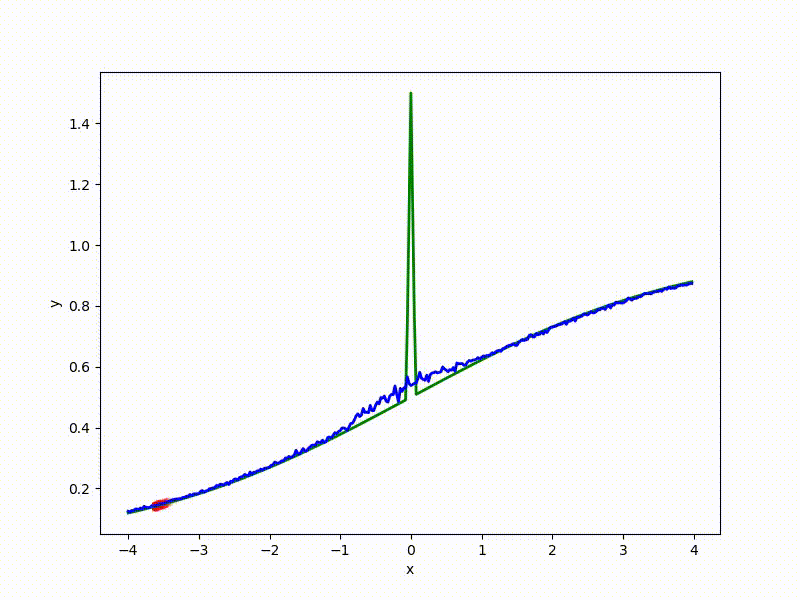
Градиентный спуск автоматически находит самый устойчивый минимум на середине плато и «туннелирует» сквозь резкий пик.

Достоинства такого подхода по сравнению с обычным градиентным спуском:

• Как уже упоминалось, $$ не обязана быть дифференцируемой. В то же время, никто не запрещает применять ES даже когда можно честно посчитать градиент.
• ES тривиально параллелится. Хоть и существуют параллельные версии SGD, они требуют пересылать веса $$ между нодами-рабочими или нодами и центральным сервером. Это очень затратно, когда слоёв много. В случае эволюционных стратегий каждая из рабочих станций может считать свой набор $$. Переслать $$ довольно просто — обычно это просто скаляры. $$ пересылать так же сложно как и $$, однако делать этого нет надобности: если всем нодам известен алгоритм сэмплирования случайных чисел и seed генератора, они могут симулировать $$ друг друга! Производительность такой системы увеличивается почти что линейно при масштабировании, что делает распределенную версию ES просто невероятно быстрой, когда доступно большое число станций для проведения обучения. OpenAI рапортует об обучении MuJoCo за 10 минут на 80 машинах с 1440 CPU.
• Сэмплирование $$ вносит шум в вычисление градиента, что делает обучение более устойчивым. Сравните с dropout'ом при обучении нейронных сетей обычным образом.
• ES не зависит от frame-skip при RL (см. например здесь) — одним гиперпараметром меньше.
• Также утверждается, что эволюционные стратегии позволяют проводить обучение легче, чем обычный SGD, когда между действием в RL и положительным откликом может пройти большое количество времени, и в шумных условиях, когда непонятно, какое изменение помогло улучшить результат (меньше проявляет себя ситуация, когда сеть в начале обучения долго не может понять, что нужно делать в виртуальном окружении и лишь дёргается на месте).

Какие же недостатки?

• Графики в статье OpenAI выглядят не так уж чтобы лучезарно. Обучение при помощи ES занимает в 2-10 раз больше эпох, чем обучение при помощи TRPO. Авторы защищаются тем, что когда доступно большое число рабочих машин затраченное реальное время оказывается в 20-60 раз меньше (хоть каждое обновление приносит меньше пользы, мы можем делать их гораздо чаще). Здорово, конечно, но где бы ещё взять 80 рабочих нод. Плюс, как будто бы итоговые результаты немного хуже. Наверное, можно «добить» сеть более точным алгоритмом?
• Шум в градиентах — палка о двух концах. Даже при одномерной оптимизации они оказываются слегка нестабильными (см. шум на синих кривых на графиках выше), что уж там говорить, когда $$ очень многомерный. Пока что непонятно, насколько серьёзную проблему это представляет, и что с этим можно сделать, кроме как увеличить размер выборки сэмплирования.
• Неизвестно, можно ли эффективно применить ES в обычном обучении с учителем. OpenAI честно сообщает, что на обычном MNIST ES может быть в 1000 (!) раз медленнее, чем обычная оптимизация.

Вариации ES

Дополнительное положительное качество эволюционных стратегий — что они лишь подсказывают нам, как считать производную, а не заставляют переписывать алгоритм обратного распространения ошибки начисто. Всё, что можно применить к backprop-SGD, можно применить и к ES: импульс Нестерова, Adam-подобные алгоритмы, batch normalization. Есть несколько специфичных дополнительных приёмов, но пока что нужно больше исследований, при каких обстоятельствах они работают:

• ES позволяет оценивать не только первую, но и вторую производную $$. Чтобы получить формулу достаточно расписать ряд Тейлора в доказательстве выше до пятого члена, а не до третьего и отнять от него полученную формулу для первой производной. Впрочем, похоже, что делать это стоит лишь из научного любопытства, так как оценка получается ужасно нестабильной, а Adam и так позволяет эмулировать действие второй производной в алгоритме.
• Не обязательно использовать нормальное распределение. Очевидные претенденты — распределение Лапласа и t-распределение, но можно придумать и более экзотические варианты.
• Не обязательно сэмплировать лишь вокруг текущего $$. Если запоминать предысторию движения по пространству параметров, можно сэмплировать веса вокруг точки немного по направлению движения.
• Во время обучения можно периодически перепрыгивать не по направлению градиента а просто в точку с наименьшим $$. С одной стороны, это дестабилизирует обучение ещё больше, с другой стороны, такой подход хорошо работает в сильно нелинейных случаях с большим количеством локальных минимумов и седловых точек.
• Статья Uber от декабря 2017 предлагает novelty reward seeking evolution strategies (NSR-ES): в формулы обновления весов добавляется дополнительный член, поощряющий новые стратегии поведения. Идея внедрения разнообразия в reinforcement learning не нова, очевидно, что её попытаются приткнуть и сюда. Получившиеся алгоритмы обучения дают заметно более хорошие результаты на некоторых играх датасета Atari.
• Также есть статья, утверждающая, что необязательно пересылать результаты со всех нод всем остальным нодам: прореженный граф общения между рабочими станциями не только быстрее работает, но и выдаёт более хорошие результаты (!). По свей видимости, общение не со всеми собратьями по обучению работает как дополнительная регуляризация наподобие dropout'а.

См. также эту статью, дополнительно размышляющую о разнице поведения ES и TRPO в ландшафтах параметров разного типа, эту статью, более подробно описывающую взаимоотношения между ES и SGD, эту статью, доказывающее внеземное происхождение египетских пирамид, и эту статью, сравнивающую ES от OpenAI с более старой классической ES.

Variational optimisation (VO)

Хм, но почему ни слова не сказано про изменение $$ во время обучения? Было бы логично уменьшать его, ведь чем дольше идёт обучение, тем ближе мы к желаемому результату, следовательно нужно больше обращать внимание на локальный ландшафт $$. Вот только как именно менять среднеквадратичное отклонение? Не хочется изобретать какую-то хитрую схему…

Оказывается, всё уже придумано! Evolution strategies — это частный случай вариационной оптимизации для фиксированного $$.

Вариационная оптимизация зиждется на вспомогательном утверждении о вариационном ограничении сверху: глобальный минимум функции $$ не может быть меньше, чем среднее по значениям $$, как бы мы эти $$ ни сэмплировали:

$$

Где $$ — вариационный функционал, глобальный минимум которого совпадает с глобальным минимумом $$. Заметьте, что теперь минимизация идёт не по исходным параметрам $$, а по параметрам распределения, из которого мы семплировали эти параметры — $$. Кроме того, обратите внимание, что даже если $$ была недифференцируема, $$ дифференцируема, если дифференцируемо распределение $$, и производную можно выразить как:

$$

$$

$$

$$

Если $$ — распределение Гаусса с фиксированной дисперсией, из этой формулы легко получить формулу для ES. Но что если $$ не фиксирована? Тогда на каждый вес в $$ у нас получается два параметра в $$: центр и среднеквадратичное отклонение соответствующей гауссианы. Размерность задачи увеличивается вдвое! Проще всего показать на одномерном примере. Вот вид сверху на получившийся после преобразования ландшафт для функции из предыдущей секции:

И спуск по нему:

Его значения в точке $$ соответствуют средним по значениям, сэмплированным из точки $$ при помощи нормального распределения со среднеквадратичным отклонением $$. Отметим, что

• Снова: в реальной жизни нет смысла считать считать эту функцию. Как и в случае ES нам нужен только градиент.
• Теперь мы минимизируем $$, а не $$.
• Чем меньше $$, тем больше сечение $$ напоминает исходную функцию $$
• Глобальный минимум $$ достигается при $$. В конечном итоге нам понадобится только $$, а $$ можно отбросить.
• В глобальный минимум одномерной функции довольно сложно попасть — он огорожен высокими стенками. Однако если начать из точки с большим $$, сделать это становится гораздо проще, так как чем больше сглаживание, тем сильнее сечение функции напоминает обычную квадратичную функцию.
• Тем не менее, лучше воспользоваться Adam, чтобы попасть в узкую ложбину минимума.

Какие преимущества даёт введение вариационной оптимизации? Оказывается, из-за того что в ES был фиксированный $$, его формула могла вести нас в сторону субоптимальных минимумов: чем больше $$, тем менее на ландшафте сглаженной функции заметны глубокие, но узкие минимумы.

Так как в VO $$ перменный, у нас есть хотя бы шанс попасть в настоящий глобальный минимум.

Недостатки очевидны: даже в самом простом случае размерность задачи увеличивается вдвое, что уж говорить про случай, когда мы хотим иметь по $$ на каждое направление. Градиенты становятся ещё более нестабильными.

Вспомните график выше со «стенкой» посередине. VO ощущает её ещё меньше:

(бывшая стенка — это маленькая штучка снизу посередине)

Хоть сходимость в глобальный минимум не гарантирована даже для простых случаев, у нас больше шансов попасть хоть куда-нибудь при неидеальной инициализации:

Или даже выбраться из участка плохой пространственной инициализации:

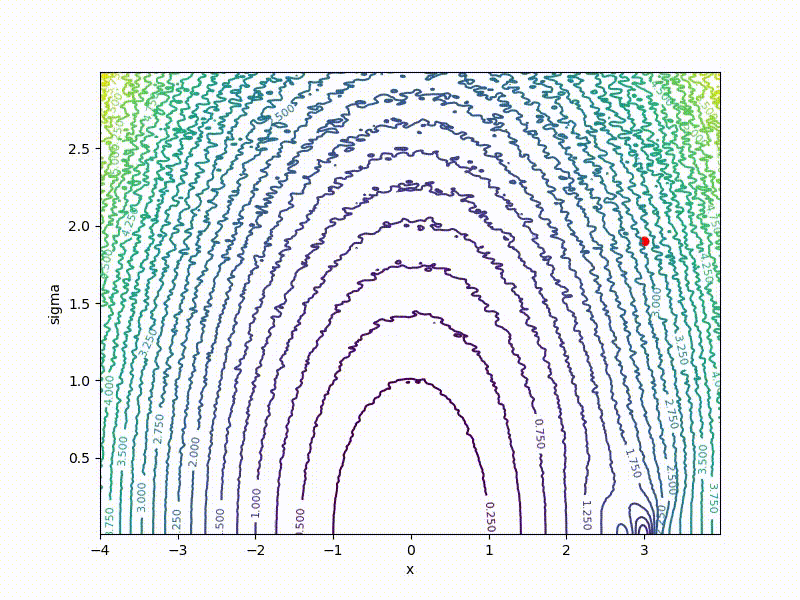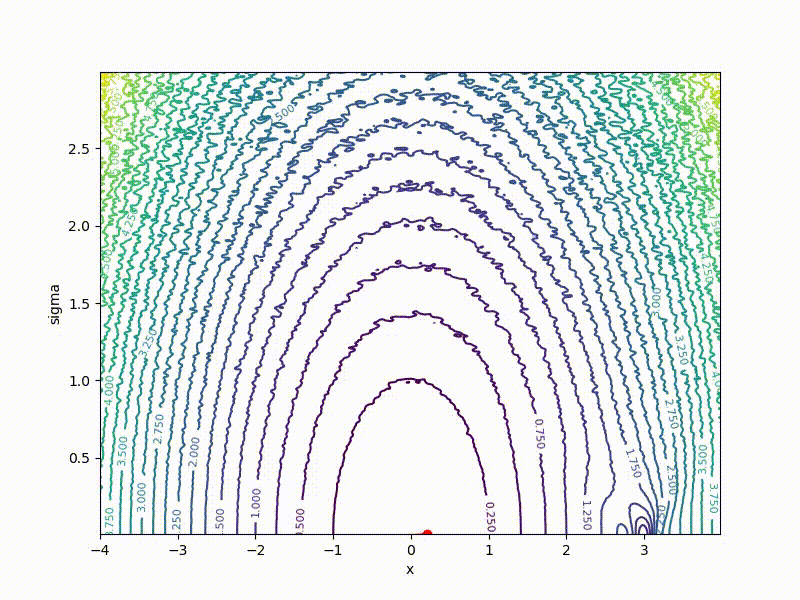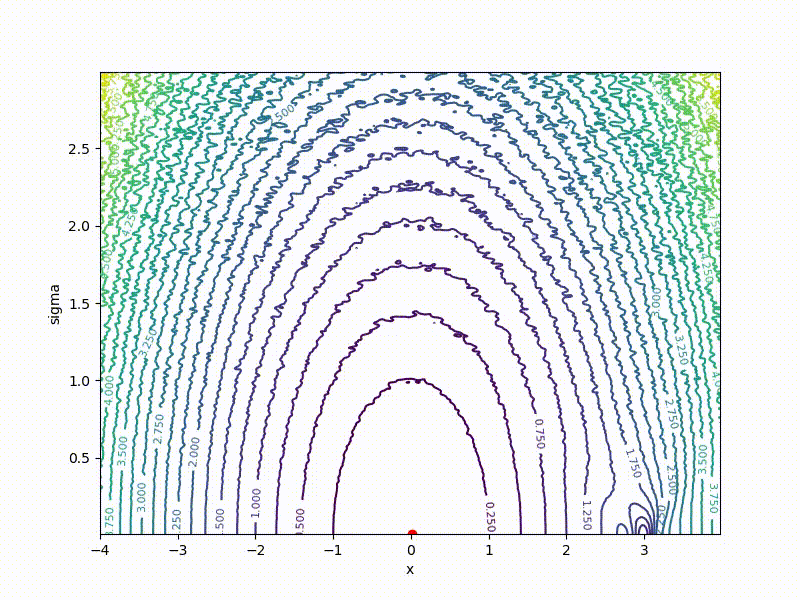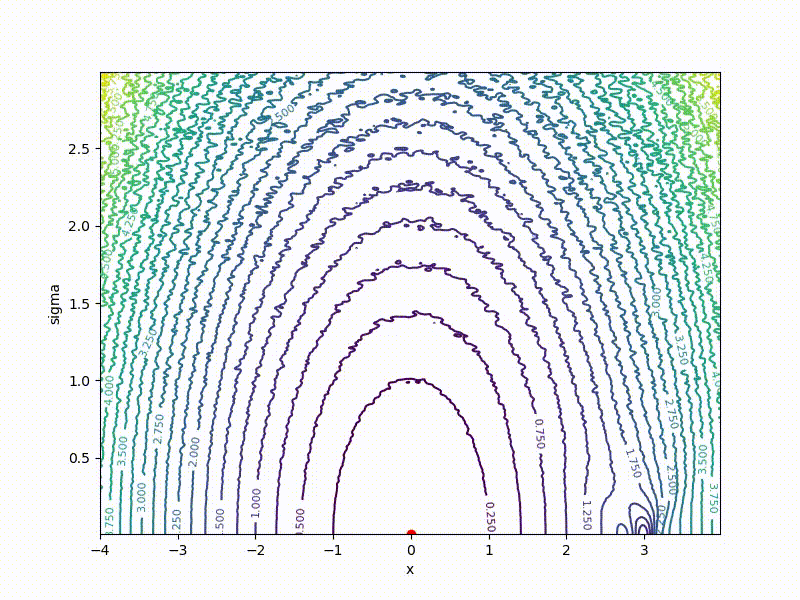
Заключение

Статья в OpenAI принесла в вариационную оптимизацию трюк с общим seed'ом генераторов случайных чисел различных нод. Но пока что (кажется?) нет статей, в которых оценивается реальное ускорение от него. Сдаётся мне, в ближайшем будущем, мы их увидим. Если они будут обнадёживающи, и если ES и VO будут распространены на обучение с учителем, быть может, нас ждёт смена парадигмы в машинном обучении.

Скачать код, с помощью которого были построены визуализации, можно здесь. Посмотреть на другие визуализации и узнать про связь вышеописанных методов с генетическими алгоритмами, Natural Evolution Strategies и Covariance-Matrix Adaptation Evolution Strategy (CMA-ES) можно здесь. Пишите в комментариях, если кому-то интересно посмотреть, как поведут себя ES и VO на какой-то определённой функции. Спасибо за внимание!