Прекрасные чудовища математики

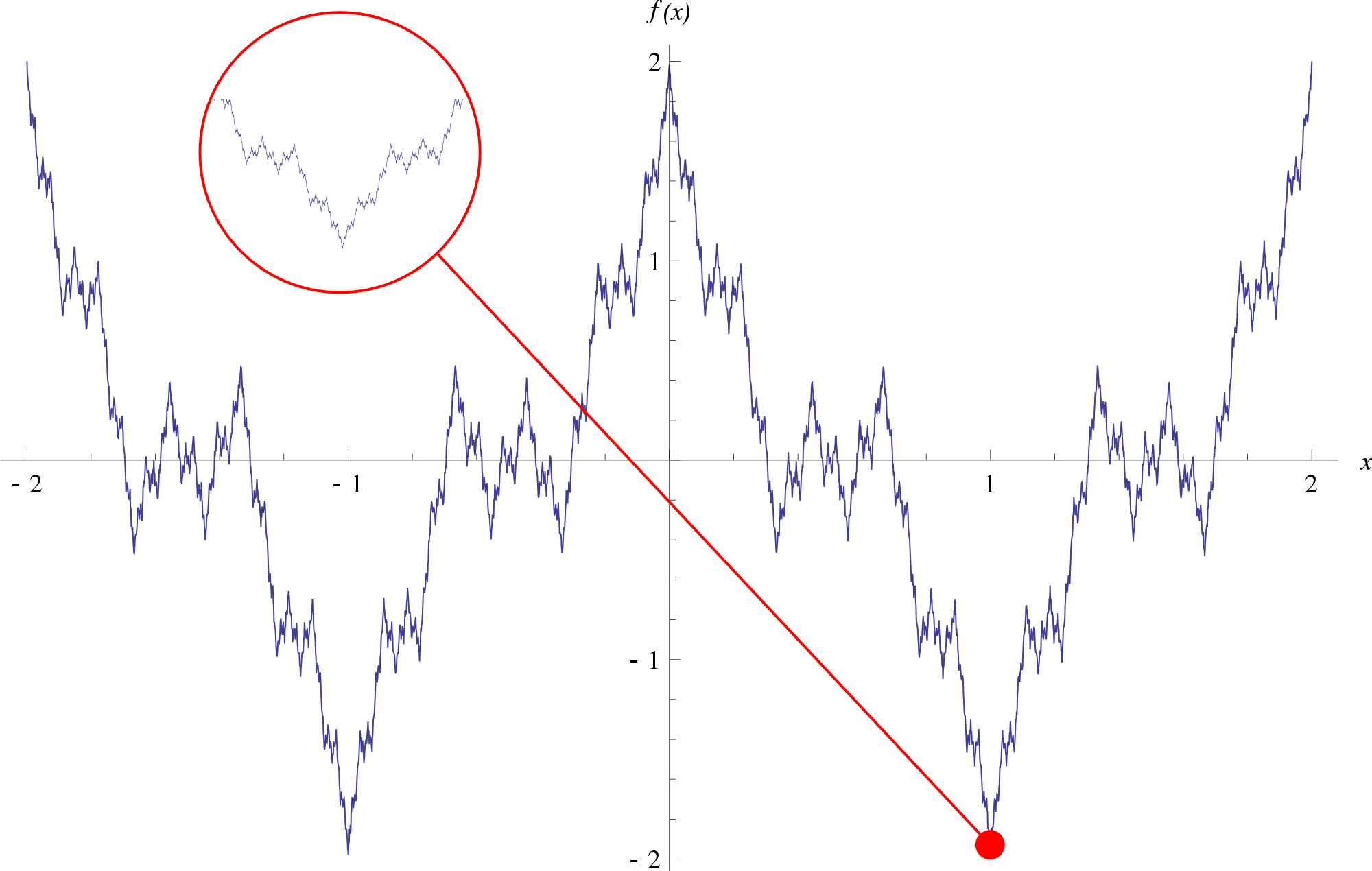
UPD: добавлен график функции.

Подобно своему создателю Карлу Вейерштрассу, это чудовище возникло из ниоткуда. Потратив четыре года учёбы в университете на кутежи и фехтование, Вейерштрасс выпустился из него с пустыми руками. В конце концов он взялся за преподавание и большую часть 1850-х был школьным учителем в Браунсберге. Ему была отвратительна жизнь в маленьком прусском городишке, он находил своё существование там одиноким. Единственной отдушиной для него стали математические задачи, над которыми он работал между уроками. Но ему не с кем было поговорить о математике, и у него не было технической библиотеки для обучения. Даже результатам его работ не удавалось покинуть пределов Браунберга. Вместо публикации в академических журналах, как это сделал бы университетский исследователь, Вейерштрасс добавлял их к школьным проспектам, пугая потенциальных учеников заумными уравнениями.

В конце концов Вейерштрасс отправил одну из своих статей в уважаемый «Журнал Крелле». Несмотря на то, что предыдущие статьи остались едва замеченными, эта вызвала огромный всплеск интереса. Вейерштрасс обнаружил способ работы с ужасным классом уравнений, известным как «абелевы функции». В статье было приведено краткое изложение его методов, но этого было достаточно, чтобы убедить математиков в наличии у автора уникального таланта. Не прошло и года, как Кёнигсбергский университет дал Вейерштрассу почётную докторскую степень, а вскоре после этого Берлинский университет предложил ему должность профессора. Несмотря на то, что Вейерштрасс проделал интеллектуальный аналог пути «из грязи в князи», многие из его старых привычек сохранились. Он редко публиковал статьи, предпочитая делиться своими работами со студентами. Но он был малопочтителен не только к процессу публикации: не пугали его и «священные коровы» математики.

Вскоре Вейерштрасс взялся за изучение работ Огюстена Луи Коши, одного из наиболее выдающихся математиков века. Во многих работах Коши исследовались математический анализ и скорости изменения (или «производные»). Он создал основы словаря математического анализа, определив важнейшие концепции этой тематики. Но когда Вейерштрасс увидел его определения, то нашёл их многословными и расплывчатыми. В них было слишком много «жестов руками» и мало подробностей.

Он решил пересмотреть словарь Коши, заменив прозу логическими условиями. Основной целью в этой его ранней работе стало переопределение производной. Для вычисления градиента кривой в точке, а значит и скорости её изменения, Исаак Ньютон изначально рассматривал прямую, проходящую через эту точку и соседнюю точку кривой. Затем он сдвигал эту соседнюю точку всё ближе и ближе, пока наклон кривой не становился равным градиенту кривой. Но эту концепцию сложно было определить математически. Что указывает на «близость» двух точек друг к другу?

По многословному определению Коши, градиент «неограниченно приближается к фиксированному значению, таким образом, что в результате отличается от него настолько, насколько это требуется». Вейерштрасс не считал, что такое описание достаточно чётко. Он хотел создать более практичное определение, поэтому решил превратить концепцию в формулу. Вместо манипуляций с абстрактными идеями математики должны иметь возможность изменить уравнения. Работая над этим, он заложил основы своего чудовища.

В ту эпоху математики во многом вдохновлялись природой. Когда Ньютон разрабатывал математический анализ, он в первую очередь вдохновлялся физическим миром: траекториями планет, колебаниями маятника, движением падающего фрукта. Такое мышление привело к возникновению геометрической интуиции относительно математических структур. Они должны были иметь такой же смысл, что и физический объект. В результате этого многие математики сосредоточились на изучении «непрерывных» функций. Их можно воспринимать как функции, которые можно нарисовать, не отрывая карандаша от бумаги. Нанесите на график скорость падающего яблока в зависимости от времени и она окажется сплошной линией, в которой не будет ни разрывов, ни резких скачков. Непрерывная функция, как считалось, была «естественной».

По общепринятому тогда мнению, у любой непрерывной кривой можно было найти градиент для любого конечного числа точек. Казалось, это соответствовало интуитивному понимаю: у линии может быть несколько неровных кусков, но всегда есть несколько частей, которые являются «гладкими». Французский физик и математик Андре-Мари Ампер даже опубликовал доказательство этого утверждения. Его аргументация была построена на том «интуитивно очевидном» факте, что непрерывная кривая имеет части, на которых она увеличивается, уменьшается или остаётся плоской. Это означало, что для этих областей можно вычислить градиент. Ампер не думал о том, что произойдёт, когда эти части становятся бесконечно малыми, но он заявил, что этого и не нужно. Его подход был достаточно общим, чтобы избежать рассмотрения "infiniment petits" (бесконечно малых) элементов. Большинству математиков такой логики было достаточно: к середине 19-го века почти в каждом учебнике по математическому анализу цитировалось доказательство Ампера.

Но в 1860-х появились слухи о странном существе — математической функции, противоречившей теореме Ампера. В Германии великий Бернхард Риман рассказывал своим студентам, что знает непрерывную функцию, не имеющую гладких частей, и для которой невозможно вычислить производную функции в любой точке. Риман не опубликовал доказательств, как и Шарль Селлерье из Женевского университета, который писал, что обнаружил что-то «очень важное и, как мне кажется, новое», однако спрятал свои работы в папку, ставшую достоянием общественности только после его смерти несколько десятков лет спустя. Однако если бы его заявлениям поверили, то это означало бы угрозу самым основам зарождавшегося математического анализа. Это существо угрожало разрушить счастливую дружбу между математической теорией и физическими наблюдениями, на которых она была основана. Матанализ всегда был языком планет и звёзд, но как может природа быть надёжным источником вдохновения, если найдутся математические функции, противоречащие основной её сути?

Чудовище окончательно родилось в 1872 году, когда Карл Вейерштрасс объявил, что нашёл функцию, являющуюся непрерывной, но не гладкой во всех точках. Он создал её, сложив вместе бесконечно длинный ряд функций косинуса:

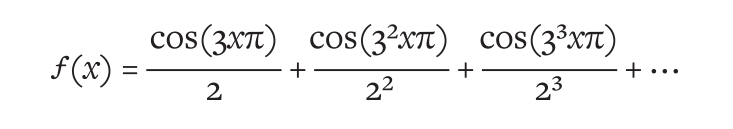Как функция она была уродливой и отвратительной. Было даже непонятно, как она будет выглядеть на графике. Но Вейерштрасса это не волновало. Его доказательство состояло не из форм, а из уравнений, и именно это делало его заявление таким мощным. Он не только создал чудовище, но и построил его на железной логике. Он взял собственное новое строгое определение производной и доказал, что для этой новой функции её вычислить невозможно.

Результат привёл математическое сообщество в состояние шока. Французский математик Эмиль Пикар сказал, что если бы Ньютон знал о таких функциях, то не создал бы математический анализ. Вместо вынашивания идей о физике природы он завяз бы в попытках пробраться через жёсткие математические преграды. Чудовище начало расшатывать и предыдущие исследования. Результаты, казавшиеся «доказанными», трещали по швам. Ампер использовал выбранные Коши пространные определения для доказательства своей теоремы о гладкости. Теперь его доказательства начинали рушиться. Неопределённые понятия прошлого были бессильны против чудовища. Ещё хуже было то, что теперь стало неочевидным, из чего же состоит математическое доказательство. Интуитивные геометрические аргументы двух прошедших веков стали бесполезными. Когда математики пытались прогнать чудовище, оно оставалось непреклонным. Одним странным уравнением Вейерштрасс показал, что физическая интуиция не была надёжным основанием для построения математических теорий.

Авторитетные математики попытались отмахнуться от результата, утверждая, что он некрасив и ненужен. Они опасались, что буквоеды и возмутители спокойствия внесут хаос в их любимую область знания. В Сорбонне Шарль Эрмит писал: «Я в отвращении и ужасе отворачиваюсь от прискорбной скверны функций, не имеющих производных». Анри Пуанкаре, впервые назвавший такие функции чудовищами, назвал работу Вейерштрасса «оскорблением здравого смысла». Он утверждал, что такие функции — нахальное отвлечение от сути предмета.

«Их изобрели с целью показать ошибочность рассуждений наших предшественников», — говорил он. «И кроме этого, мы не сможем ничего из них взять».

Многие из «старой гвардии» хотели оставить чудовище Вейерштрасса на задворках математики. Мешало и то, что никто не мог представить облик животного, с которым они встретились — только после изобретения компьютеров появилась возможность создать его график. Его непостижимая форма мешала осознанию математическим сообществом того, как такая функция вообще может существовать. Кроме того, стиль доказательства Вейерштрасса был неизвестен многим математикам. Его доказательство содержало десятки логических шагов и простиралось на несколько страниц. Цепочка рассуждений была едва уловимой и требовала серьёзных технических знаний, а в реальном мире аналогов, которые бы помогли в понимании, не было. Инстинкт призывал избегать этого доказательства.

Но чудовища имеют обычай прокладывать дорогу самостоятельно. На самом деле многие концепции, кажущиеся сегодня очевидными, даже необходимыми, когда-то были чудовищами. Веками математики отвергали отрицательные числа. Древние греки, в основном работавшие с геометрией, не видели в них нужды. То же самое справедливо и для средневековых академиков, перенявших идеи греков. Тень этого монстра иногда мелькает и сегодня, например, в вопросах ребёнка, спрашивающего, почему при умножении двух отрицательных чисел получается положительное. Но в целом мы приручили этого зверя: никто не мечтает снова его изгнать.

То же самое случилось с чудовищем Вейерштрасса — оно начало получать призвание. В 1904 году Альберт Эйнштейн познакомил физиков с идеей «броуновского движения»: он сказал, что частицы в жидкости следуют по случайным путям, потому что молекулы жидкости постоянно их отталкивают. Столкновения настолько часты (больше 1021 в секунду), что как бы ни был хорош микроскоп или тщательно наблюдение, траектории никогда не будут плавными. С практической точки зрения, для них невозможно найти производную. Если исследователи хотят работать с такими задачами, то им придётся столкнуться с чудовищем Вейерштрасса. Именно так и поступил Эйнштейн. Его теория заключалась в том, что в броуновском движении использовались бесконечно ломаные функции. Это стало важным прецедентом: с тех пор физики использовали в качестве приближения к броуновскому движению негладкие функции.

Когда стало очевидно, что так называемые «функции Вейерштрасса» на самом деле достаточно полезны, учёные начали разрабатывать способы элегантной работы с негладкими функциями. Вместо того, чтобы анализировать путь отдельной частицы в жидкости, они стали рассматривать среднее поведение множества частиц. Насколько далеко они могут переместиться? Когда они могут достичь заданной точки? За пределами области изучения броуновского движения математики также начали переосмысливать основные инструменты матанализа. Скорость изменений всегда определялась относительно расстояний, а площадь под кривой измерялась геометрически. Но когда функции были негладкими, то такие идеи не имели смысла.

Киёси Ито из Токийского университета обнаружил способ обойти проблему, подойдя к ней с точки зрения вероятностей. Это была неортодокасальная, если не сказать рискованная, тактика: в 1940-х едва ли кто-то считал теорию вероятности серьёзной областью. Однако Ито настаивал на своём. Он подошёл к функциям как к случайным процессам и перевёл определения Вейерштрасса на новый язык, основанный на вероятностях. Он заявил, что два случайных процесса «близки» друг к другу, если их ожидаемые результаты одинаковы. Он ввёл метод работы с математической функцией, зависящий от величины негладкости, как в броуновском движении, вместо более традиционной переменной, например, расстояния. С помощью своих новых методов он вывел «лемму Ито» для вычисления изменения такой функции со временем.

К 1970-х его работа развернулась в совершенно новую область математики, называемую стохастическим исчислением (математики любят называть всё связанное со случайностью «стохастическим»). Как и в самом матанализе, в ней появился совершенно новый набор инструментов и теорем. Сегодня стохастическое исчисление используется для изучения всевозможных явлений, от работающих в мозге нейронов до распространения заболеваний в популяции. Также оно стало основой финансовой математики, в которой помогает банкам оценивать стоимость опционов. Оно может учитывать неровное поведение биржевого курса, а значит, показывает, насколько меняется со временем ценность опциона. Получившееся уравнение, которое известно как формула Блэка-Шоулза, теперь используется на всех торговых площадках мира. Однако Ито всегда вводили в замешательство похвалы банкиров. Он был математиком-теоретиком, и не ожидал, что его работа станет известной благодаря практическому применению.

Чудовище Вейерштрасса перетряхнуло и принципы геометрии. В конце 19-го века шведский математик Хельге фон Кох заинтересовался идеей негладких функций, но хотел изучить их форму. Он приступил к созданию формы (а не функции), которая нигде не будет гладкой, таким образом показав, что те же монстры скрываются и в алгебре с геометрией. Хоть он и не смог нарисовать функцию Вейерштрасса, но ему удалось запечатлеть её близкого родственника. Работая над этой задачей в процессе постоянного поиска временных работ на должности преподавателя-стажёра, фон Кох в 1904 году обнаружил своё существо. Он взял равносторонний треугольник, затем добавил с каждой стороны три меньших треугольника, и так до бесконечности. Получившаяся геометрическая форма была непрерывной, но не имела производных. Благодаря своему выдающемуся внешнему виду фигура быстро стала известна как «снежинка Коха».

Коху удалось расширить власть чудовища Вейерштрасса за пределы мира уравнений и функций. Но в результате его работы было ещё кое-что, заслуживавшее внимания. При более близком изучении оказалось, что у его снежинки было любопытное самоподобие: увеличьте одну часть снежинки, и она будет выглядеть так же, как бо?льшая фигура. Спустя много лет стало очевидно, что функция Вейерштрасса обладает тем же свойством.

По прошествии времени такое самоподобие стало проявляться во всевозможных явлениях. Для популяризации идеи «фрактальных» объектов в 1980-х потребовалась основополагающая работа Бенуа Мандельброта. Такие объекты имеют формы, повторяющиеся во всё меньших и меньших масштабах. Береговые линии, облака, растения, кровяные сосуды — математики обнаружили, что фракталы вездесущи в природе. Как и снежинка Коха, ни один из них не был гладким. Да и как бы они были гладкими? Если фигура имеет гладкие части, то паттерн при достаточном увеличении исчезнет. Как обнаружил Кох, простейшим способом получения негладкой фигуры является создание фрактального объекта. Возможно, работа Вейерштрасса должна была неизбежно направить математиков в сторону изучения самоподобных паттернов, познакомив исследователей с миром изысканных, прекрасных структур.

Чудовище Вейерштрасса продолжает свою работу и по сей день. Уравнения Навье-Стокса описывают движение жидкости и лежат в основе современной динамики жидкостей и аэродинамики, управляющих всем — от конструкции самолётов до прогнозирования погоды. Однако несмотря на то, что они впервые были созданы в 1840-х, математики до сих пор не знаю, всегда ли их можно решить. В 2000 году Математический институт Клэя предложил премию в 1 миллион долларов любому, кто докажет, что эти уравнения всегда имеют гладкие решения — или найдёт пример обратного. Эта задача считается одной из шести самых важных выдающихся задач математики, потому что несмотря на широкое использование уравнений Навье-Стокса, математики не знают, всегда ли эти уравнения дают физически достоверные результаты. Премия в 1 миллион долларов до сих пор никем не востребована. Во многих смыслах это плата за голову, провоцирующая математиков на охоту за опасными чудовищами.

В различных областях: от динамики жидкостей до финансового сектора существа, подобные функции Вейерштрасса, ставили под сомнение наши взгляды на связь между математикой и естественным миром. Математики, жившие во времена Вейерштрасса, полагали, что самая полезная математика вдохновляется природой, и что работа Вейерштрасса не вписывается в это определение. Но стохастическое исчисление и фракталы Мандельброта доказали их неправоту. Оказалось, что в реальном мире — в хаотичном, сложном реальном мире — чудовища прячутся повсюду. Как сказал Мандельброт, «природа сыграла с математиками шутку». Даже сам Вейерштрасс стал жертвой этого трюка. Он создал свою функцию, чтобы возразить, что математика должна основываться только на физических наблюдениях. Его последователи полагали, что Ньютон был ограничен интуитивным восприятием реального мира, и теперь они, свободные от этих ограничений, смогут открыть более универсальные и элегантные новые теории. Они думали, что математике больше не нужна будет природа. Но чудовище Вейерштрасса доказало, что всё обстоит совершенно наоборот. Связь математики и природы намного более глубока, чем кто-либо мог представить.

Об авторе: Адам Кучарски — научный сотрудник Лондонской школы гигиены и тропической медицины, занимающийся математической эпидемиологией.

Источник: geektimes.ru

Комментарии: