Автоэнкодер в задачах кластеризации политических событий

Уже несколько лет подряд алгоритмы машинного обучения находят применение в различных областях. Одной из таких областей может стать и аналитика различных событий в политической сфере, например: прогнозирование результатов голосования, разработка механизмов кластеризации принятых решений, анализ деятельности политических акторов. В этой статье я постараюсь поделиться результатом одного из исследований в этой области.

Постановка задачи

Современные средства машинного обучения позволяют трансформировать и визуализировать большой объем данных. Этот факт позволил провести анализ деятельности политических партий путем трансформирования голосований за 4 года в самоорганизуемое пространство точек отображающее поведение каждого из депутатов.

Каждый политик самовыразился по факту двенадцати тысяч голосований. Каждое голосование может принимать одно из пяти вариантов (не пришел в зал, пришел но пропустил голосование, проголосовал “за”, “против” или воздержался).

Наша задача — трансформировать все результаты голосования в точку в трехмерном евклидовом пространстве отражающую некую взвешенную позицию.

Open Data

Все изначальные данные были получены на официальном сайте, после чего трансформированы в данные для нейросети.

Автоэнкодер

Как было видно из постановки задачи, необходимо двенадцать тысяч голосований представить в виде вектора размерности 2 или 3. Именно категориями 2х мерных и 3х мерных пространств человек может оперировать, большее количество пространств человеку крайне сложно себе представить.

Для снижения разрядности мы применим автоэнкодер.

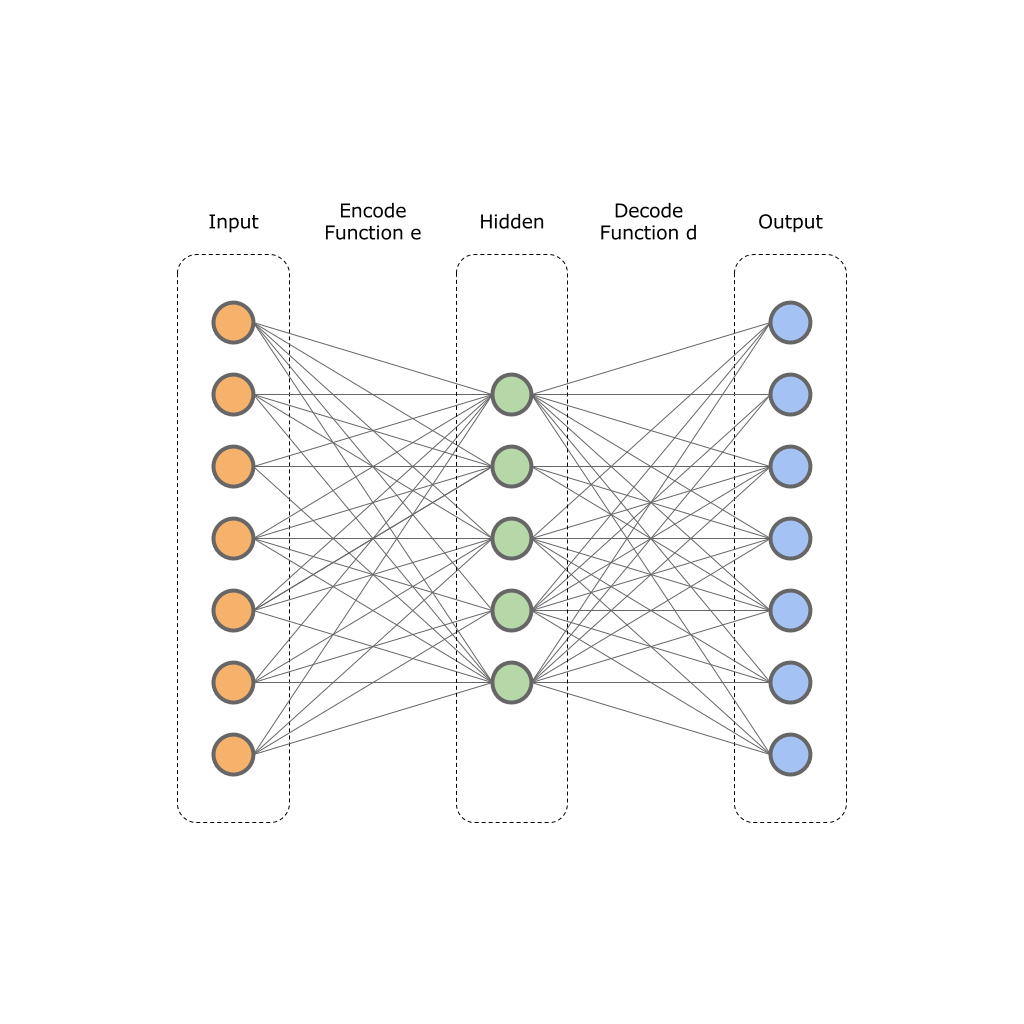
В основу автоэнкодеров заложен принцип двух функций:

— функция энкодер;

— функция декодер;

На вход такой сети подается оригинальный вектор размерностью и нейросеть трансформирует его в значение скрытого слоя размерностью . Далее декодер нейросети трансформирует значение скрытого слоя в выходной вектор размерностью , при этом . То есть скрытый слой в результате будет меньшей размерности, но при этом он сможет отражать весь набор исходных данных.

Для обучения сети используется целевая функция ошибки:


Другими словами мы минимизируем разность между значениями входного и выходного слоя. Обученная нейронная сеть позволяет сжимать размерность изначальных данных до некой размерности на скрытом слое .

На данной картинке изображен один входной, один спрятанный и один выходной слой. На практике таких слоев может быть больше.

Теорию я постарался рассказать, перейдем к практике.

Наши данные уже собраны в JSON формате с официального сайта, и закодированы в вектор.

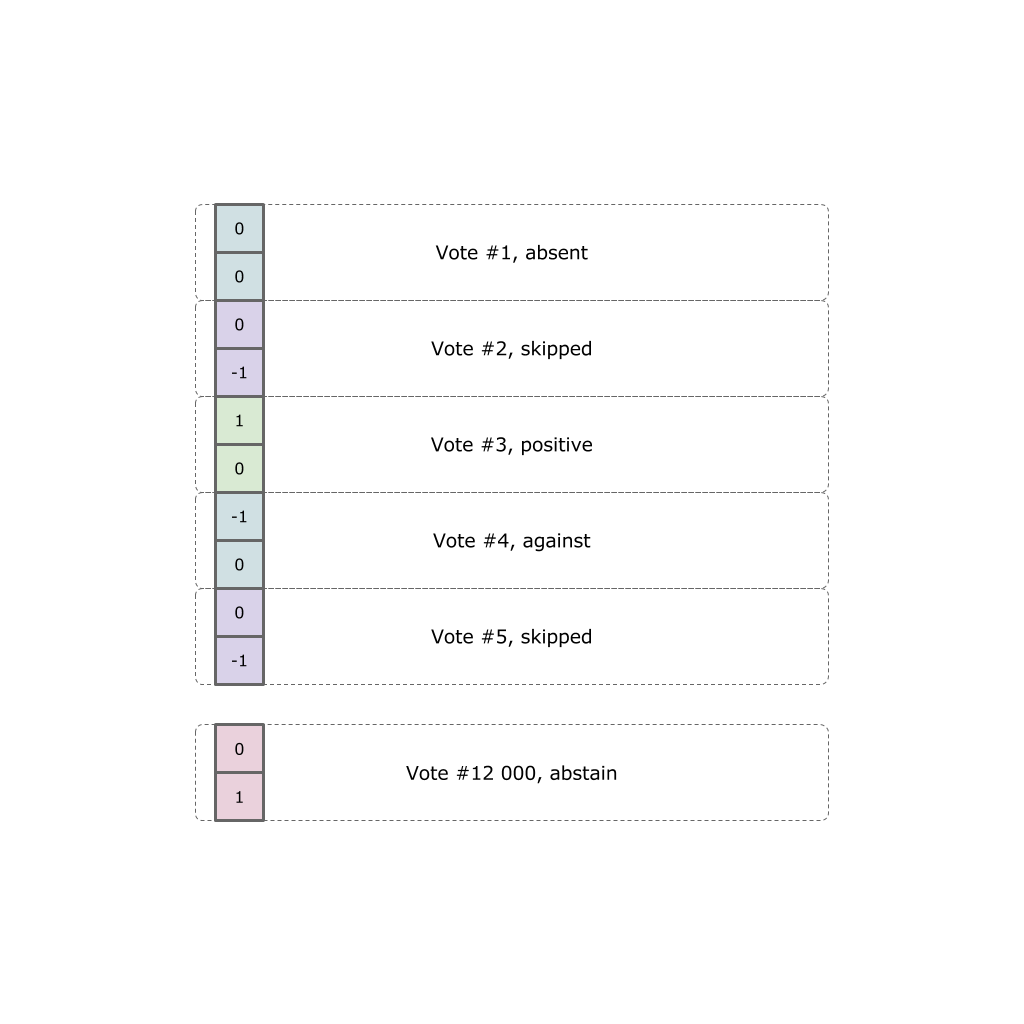
Теперь у нас есть датасет размерностью 24000 x 453. Создаем нейросеть средствами TensorFlow:

# Building the encoder def encoder(x):     with tf.variable_scope('encoder', reuse=False):         with tf.variable_scope('layer_1', reuse=False):             w1 = tf.Variable(tf.random_normal([num_input, num_hidden_1]), name="w1")             b1 = tf.Variable(tf.random_normal([num_hidden_1]), name="b1")             # Encoder Hidden layer with sigmoid activation #1             layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, w1), b1))          with tf.variable_scope('layer_2', reuse=False):             w2 = tf.Variable(tf.random_normal([num_hidden_1, num_hidden_2]), name="w2")             b2 = tf.Variable(tf.random_normal([num_hidden_2]), name="b2")             # Encoder Hidden layer with sigmoid activation #2             layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w2), b2))                  with tf.variable_scope('layer_3', reuse=False):             w2 = tf.Variable(tf.random_normal([num_hidden_2, num_hidden_3]), name="w2")             b2 = tf.Variable(tf.random_normal([num_hidden_3]), name="b2")             # Encoder Hidden layer with sigmoid activation #2             layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, w2), b2))             return layer_3  # Building the decoder def decoder(x):     with tf.variable_scope('decoder', reuse=False):         with tf.variable_scope('layer_1', reuse=False):             w1 = tf.Variable(tf.random_normal([num_hidden_3, num_hidden_2]), name="w1")             b1 = tf.Variable(tf.random_normal([num_hidden_2]), name="b1")             # Decoder Hidden layer with sigmoid activation #1             layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, w1), b1))          with tf.variable_scope('layer_2', reuse=False):             w1 = tf.Variable(tf.random_normal([num_hidden_2, num_hidden_1]), name="w1")             b1 = tf.Variable(tf.random_normal([num_hidden_1]), name="b1")             # Decoder Hidden layer with sigmoid activation #1             layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w1), b1))                      with tf.variable_scope('layer_3', reuse=False):             w2 = tf.Variable(tf.random_normal([num_hidden_1, num_input]), name="w2")             b2 = tf.Variable(tf.random_normal([num_input]), name="2")             # Decoder Hidden layer with sigmoid activation #2             layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, w2), b2))             return layer_3  # Construct model encoder_op = encoder(X) decoder_op = decoder(encoder_op)  # Prediction y_pred = decoder_op # Targets (Labels) are the input data. y_true = X  # Define loss and optimizer, minimize the squared error loss = tf.reduce_mean(tf.pow(y_true - y_pred, 2)) tf.summary.scalar("loss", loss) optimizer = tf.train.RMSPropOptimizer(learning_rate).minimize(loss) 

Полный листинг автоэнкодера.

Сеть будет обучена RMSProb оптимизатором с шагом 0.01.
В результате можем видеть граф операций TensorFlow.

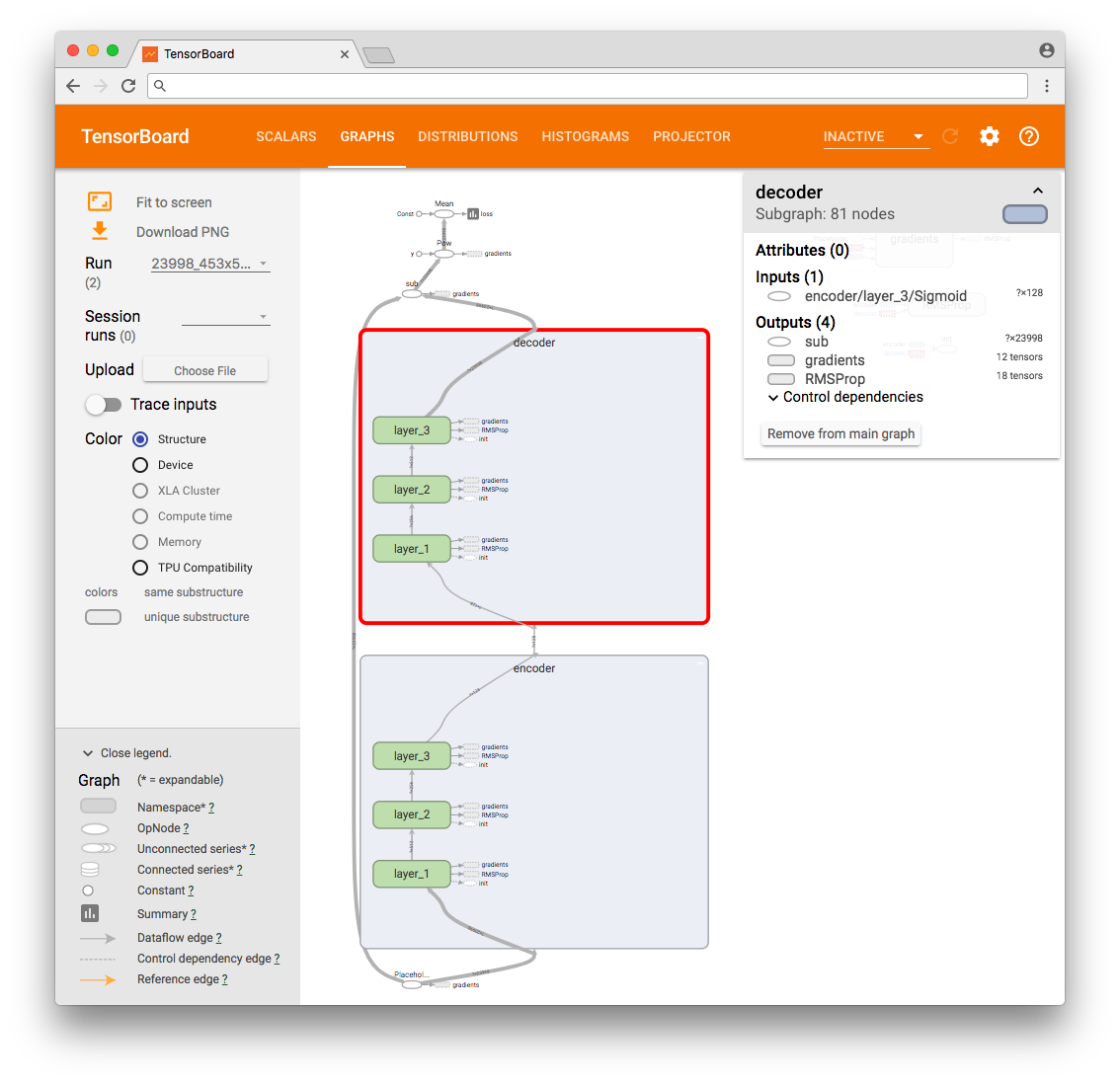
Для дополнительного теста выбираем первые четыре вектора и интерпретируем их значения на входе сети и выходе в виде картинки. Так мы сможем визуально убедиться, что значения выходного слоя “идентичны” (с погрешностью) значениям входного слоя.

Оригинальные входные данные.

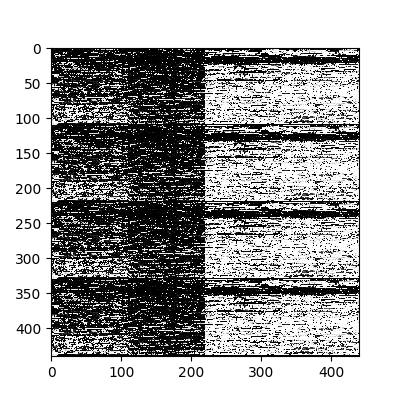
Значения выходного слоя нейросети.

После последовательно передаем все наши исходные данные в сеть, извлекая значения спрятанного слоя. Эти значения и будут нашими искомыми сжатыми данными.

К слову сказать, я пробовал подобрать различные слои и выбрал ту конфигурацию, которая позволила приблизиться к минимальной ошибке.

PCA и t-SNA редьюсеры размерности.
На этом этапе у нас есть 450 векторов с размерностью 128. Это уже очень хороший результат, но недостаточный, чтобы отдать человеку. По этой причине “идем глубже”. Будем использовать подходы PCA и t-SNA понижения размерности. Про метод главных компонентов (principal component analysis, PCA) написано много статей, поэтому на его разборе останавливаться я не буду, а вот про t-SNA подход мне бы хотелось рассказать.

Оригинальный документ Visualizing data using t-SNE содержит детальное описание алгоритма, для примера я рассмотрю вариант понижения двухмерной размерности в одномерную.

Имея двухмерное пространство и три класса A, B, C расположенные в этом пространстве, попробуем просто спроецировать классы на одну из осей:

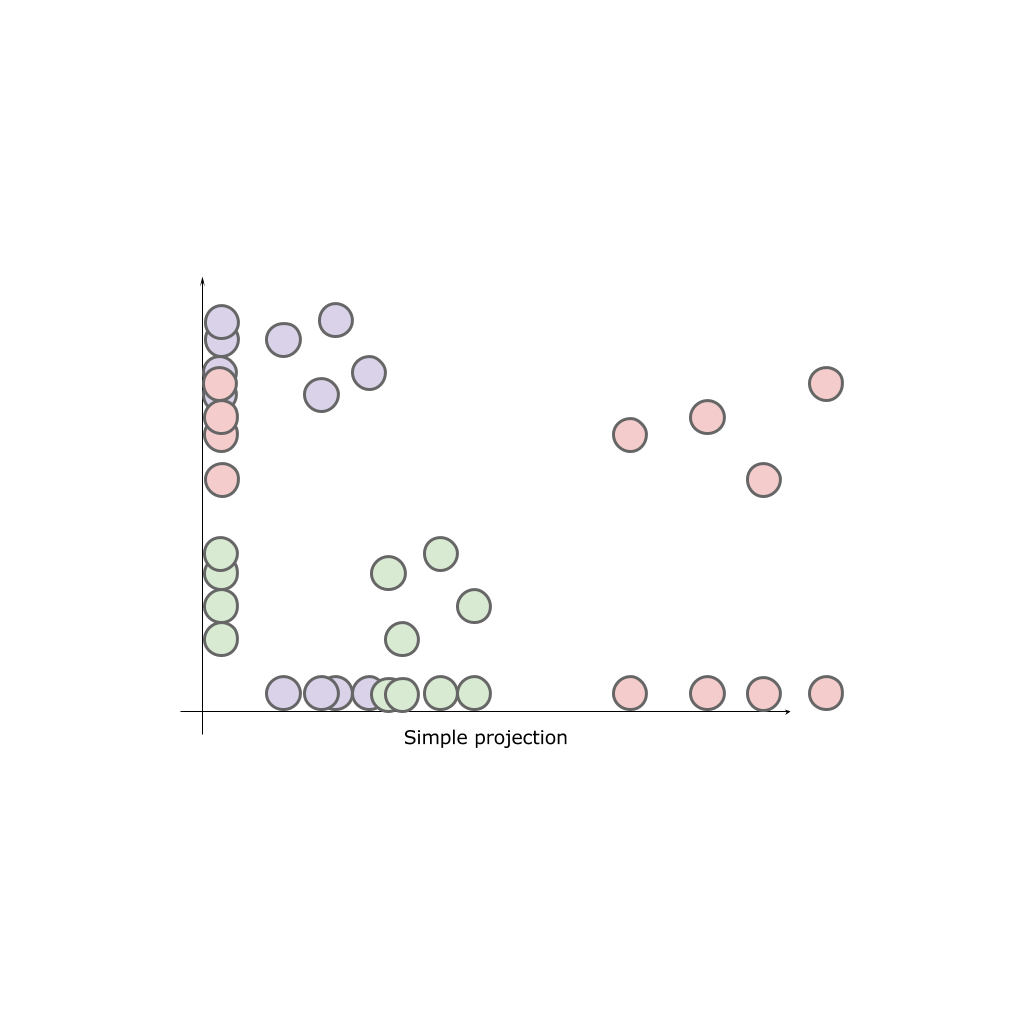
В результате ни одна ось не может дать нам полной картины исходных классов. Классы “смешиваются”, а значит теряют свои природные свойства.

Наша задача — разместить элементы в нашем конечном пространстве пропорционально удаленно (приближенно) к тому, как они были размещены в исходном пространстве. То есть те, что находились близко друг к другу так и должны быть ближе, нежеле те, что располагались на удалении.

Stochastic Neighbor Embedding

Выразим изначальное отношение между точками в первоначальном пространстве как расстояние в эвклидовом пространстве между точками , :
и соответственно для точек в искомом пространстве.

Определим условную вероятность сходства (conditional probabilities that represent similarities) точек в исходном пространстве:


Это выражение характеризует, насколько близка точка к точке при условии, что расстояние до ближайших точек класса мы характеризуем как гауссовое распределение вокруг с заданной дисперсией (центрированное на точке ). Дисперсия уникальна для каждой точки и рассчитывается отдельно исходя из того, что точки с большей плотностью имеют меньшую дисперсию.

Далее описываем сходство точки с точкой в новом пространстве соответственно:


Опять же, поскольку нас интересует только моделирование парных сходств, положим .
Если точки отображения и правильно моделируют сходство между высокоразмерными точками данных и , условные вероятности и будут равны. Мотивированный этим наблюдением, SNE стремится найти низкоразмерное представление данных, которое минимизирует несоответствие между и .
Алгоритм находит значения дисперсии для гауссова распределения в каждой конкретной точки . Маловероятно, что существует одно значение , которое является оптимальным для всех точек в наборе данных, поскольку плотность данных может изменяться. В плотных областях меньшее значение обычно более уместно, чем в более разреженных областях. SNE при помощи бинарного поиска подбирает .
Поиск происходит при учете меры эффективных соседей (параметра перплексии) которые будут приняты во внимание при расчете .
Авторы алгоритма находят пример в физике, описывая данный алгоритм как связку объектов различными пружинами, которые способны притягивать и отталкивать от себя другие объекты. Оставив систему на некое время, она самостоятельно найдет точку покоя, сбалансировав натяжение всех пружин.

t-Distributed Stochastic Neighbor Embedding

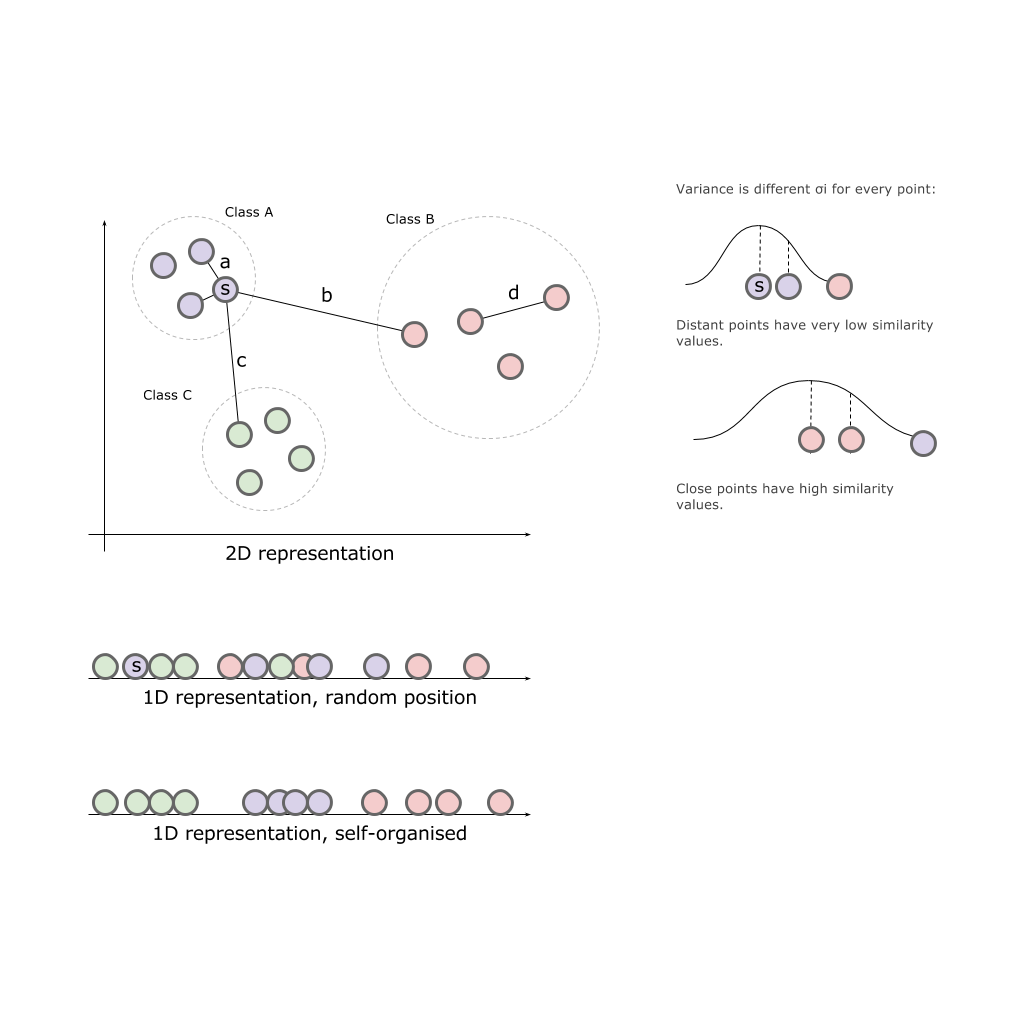
Отличие SNE от t-SNE алгоритма заключается в замене гауссова распределения на Распределение Стьюдента (оно же t-Distribution, t-Student distribution) и изменении функции ошибки на симметризированную.

Таким образом, алгоритм сперва размещает все исходные объекты в пространстве меньшей размерности. После начинает перемещать объект за объектом, опираясь на то, как далеко (близко) они находились к другим объектам в исходном пространстве.

TensorFlow, TensorBoard и Projector

Сегодня нет необходимости реализовывать подобные алгоритмы самостоятельно. Мы можем воспользоваться уже готовыми математическими пакетами scikit, matlab или TensorFlow.

Я писал в предыдущей статье, что в набор инструментов TensorFlow входит пакет для визуализации данных и процесса обучения TensorBoard.

Так что воспользуемся именно этим решением.

import os import numpy as np import tensorflow as tf from tensorflow.contrib.tensorboard.plugins import projector  # Create randomly initialized embedding weights which will be trained. first_D = 23998 # Number of items (size). second_D = 11999 # Number of items (size).  DATA_DIR = '' LOG_DIR = DATA_DIR + 'embedding/'  first_rada_input = np.loadtxt(DATA_DIR + 'result_' + str(first_D) + '/rada_full_packed.tsv', delimiter='	') second_rada_input = np.loadtxt(DATA_DIR + 'result_' + str(second_D) + '/rada_full_packed.tsv', delimiter='	')  first_embedding_var = tf.Variable(first_rada_input, name='politicians_embedding_' + str(first_D)) second_embedding_var = tf.Variable(second_rada_input, name='politicians_embedding_' + str(second_D))  saver = tf.train.Saver() with tf.Session() as session:     session.run(tf.global_variables_initializer())     saver.save(session, os.path.join(LOG_DIR, "model.ckpt"), 0)  config = projector.ProjectorConfig()  # You can add multiple embeddings. Here we add only one. first_embedding = config.embeddings.add() second_embedding = config.embeddings.add()  first_embedding.tensor_name = first_embedding_var.name second_embedding.tensor_name = second_embedding_var.name  # Link this tensor to its metadata file (e.g. labels). first_embedding.metadata_path = os.path.join(DATA_DIR, '../rada_full_packed_labels.tsv') second_embedding.metadata_path = os.path.join(DATA_DIR, '../rada_full_packed_labels.tsv')  first_embedding.bookmarks_path = = os.path.join(DATA_DIR, '../result_23998/bookmarks.txt') second_embedding.bookmarks_path = = os.path.join(DATA_DIR, '../result_11999/bookmarks.txt')  # Use the same LOG_DIR where you stored your checkpoint. summary_writer = tf.summary.FileWriter(LOG_DIR)  # The next line writes a projector_config.pbtxt in the LOG_DIR. TensorBoard will # read this file during startup. projector.visualize_embeddings(summary_writer, config) 

Результат можно посмотреть на моем TensorBoard Projector.

1. Работает в Chrome.
2. Открываем и нажимаем на Bookmarks в нижнем правом углу.
3. В верхнем правом углу можем фильтровать классы.
4. Ниже GIF картинки с примерами.

Так же сейчас доступен целый портал — projector, позволяющий визуализировать имеющийся у вас датасет непосредственно на сервере Google.

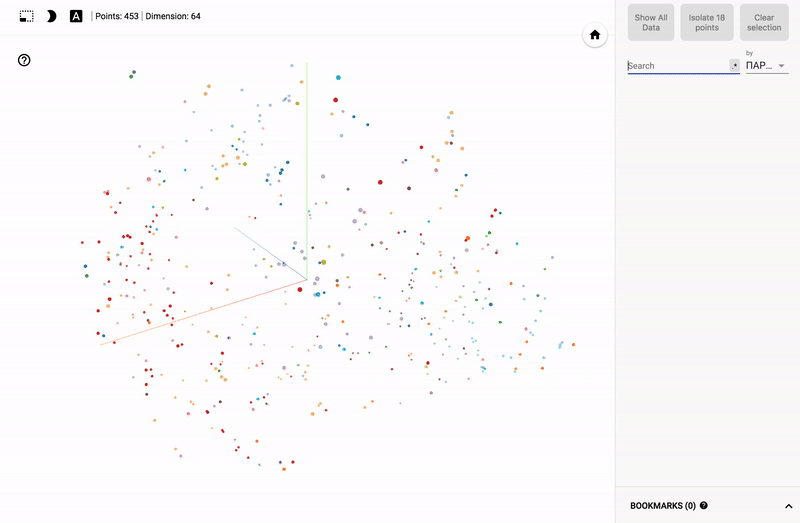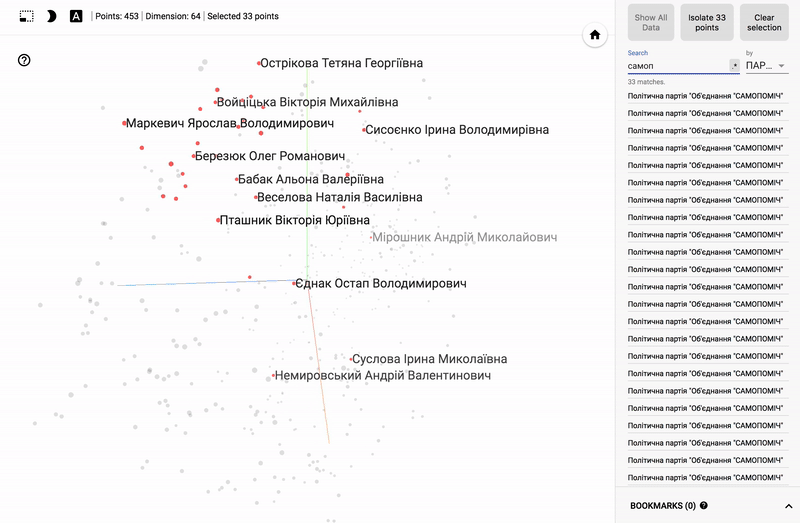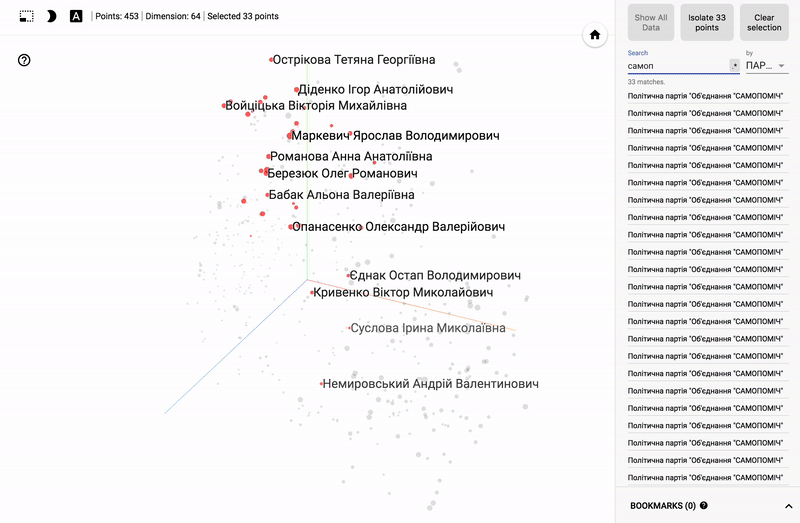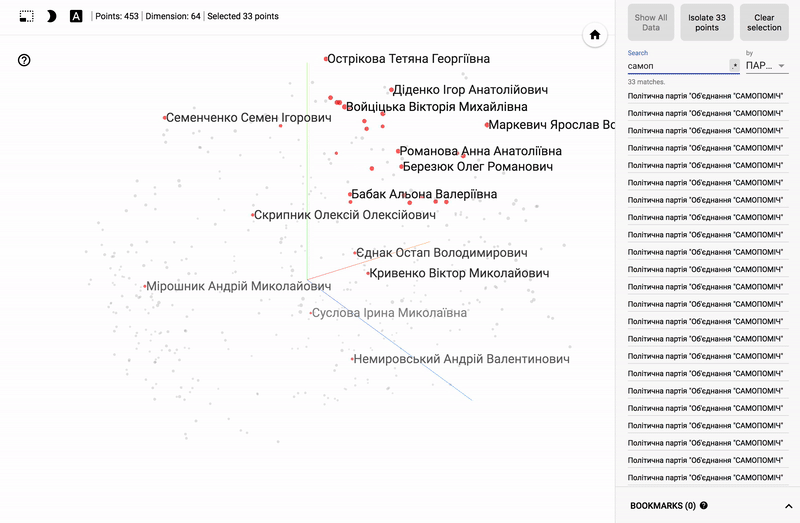
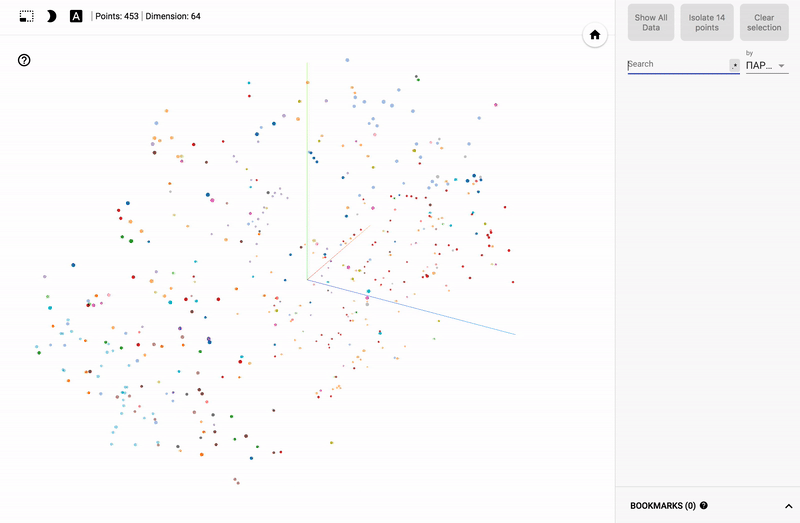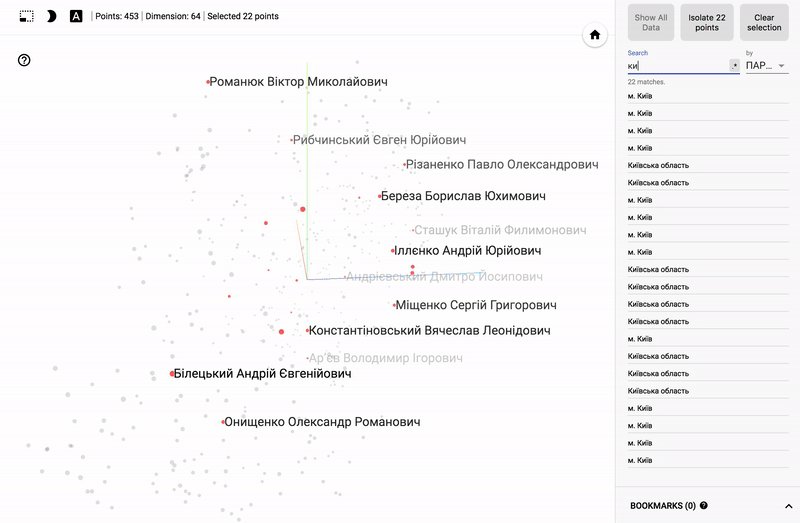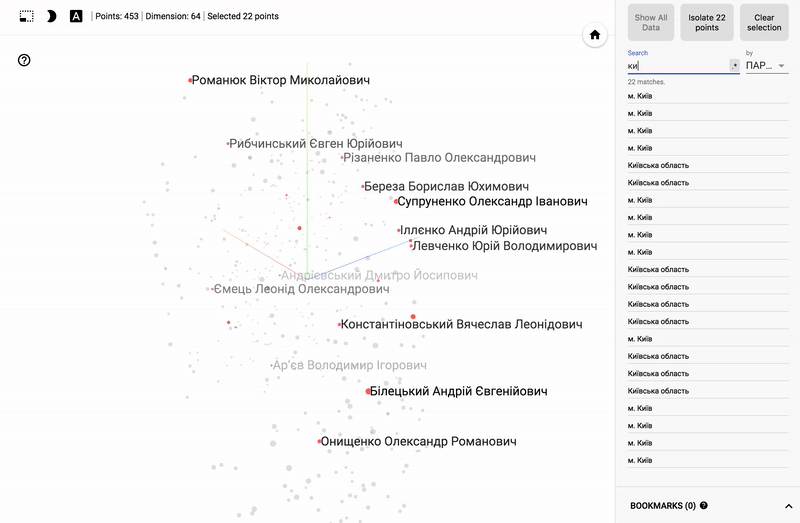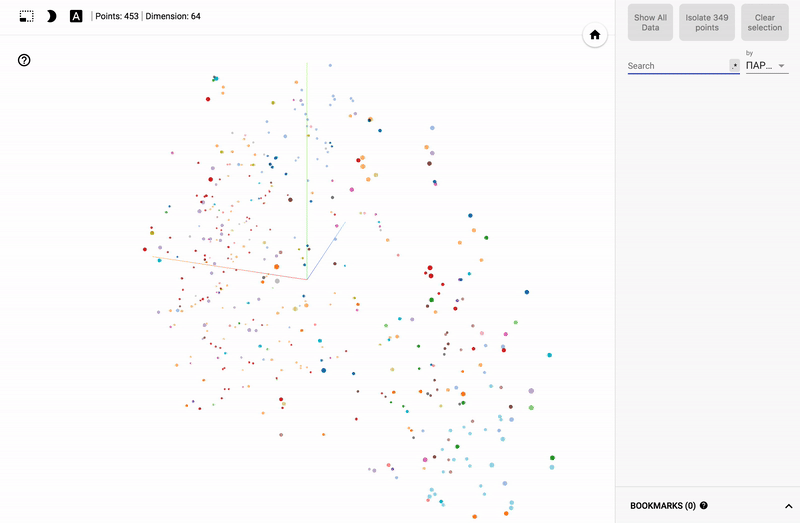
1. Заходим на сайт projector
2. Нажимаем “Load data”
3. Выбираем наш датасет с векторами
4. Добавляем собранные заранее метаданные: labels, classes и тд.
5. Подключаем цветовую дифференциацию (color map) по одному из столбцов.
6. При желании добавляем json config файл и публикуем данные для публичного просмотра.

Осталось отправить ссылку вашему аналитику.

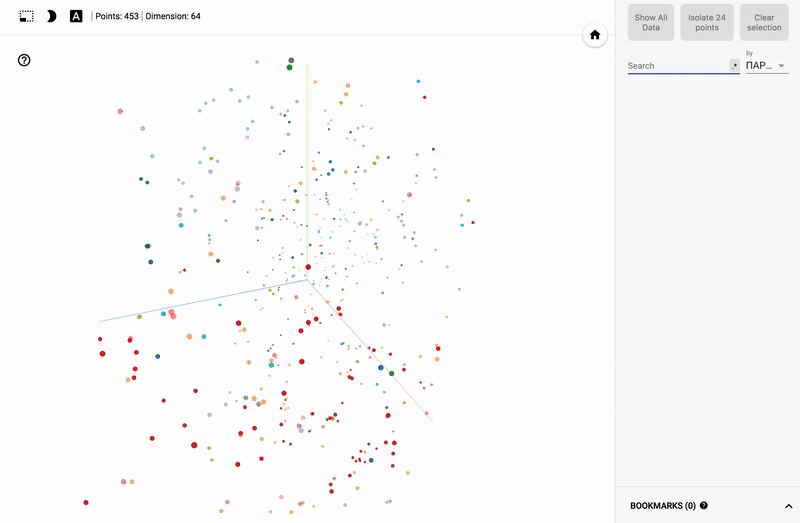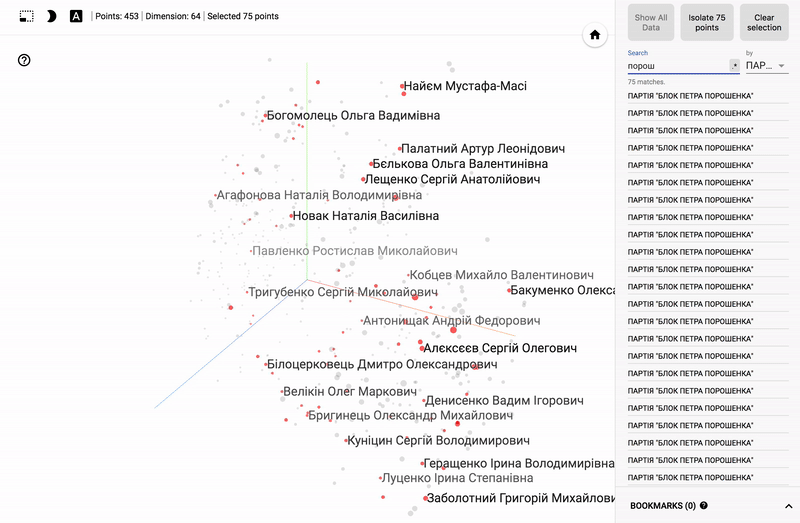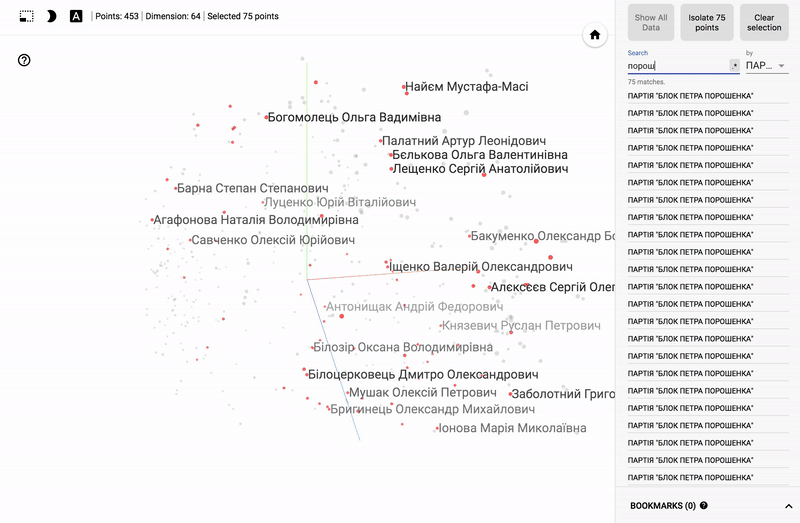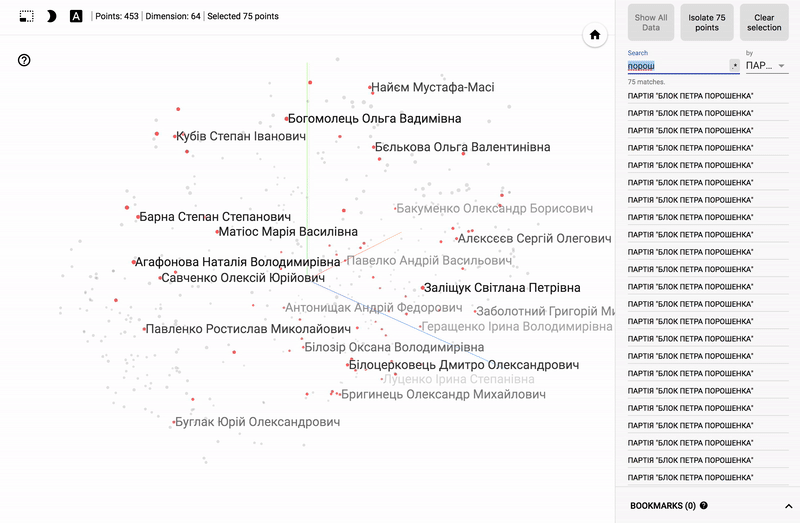
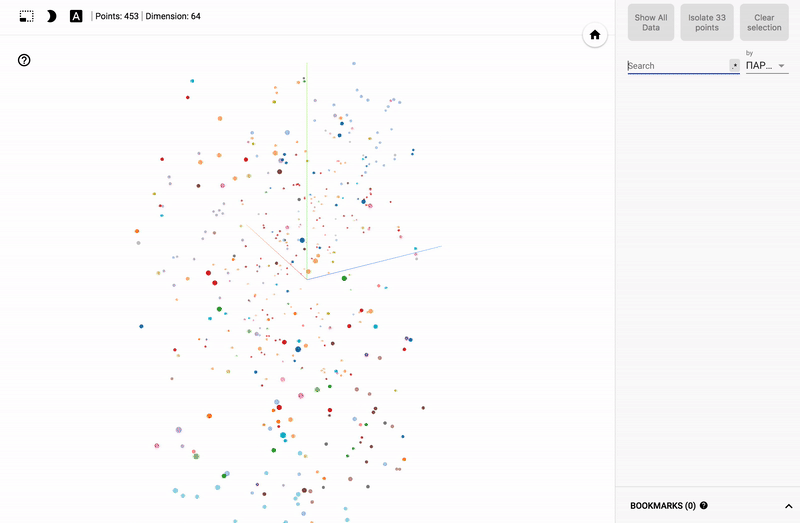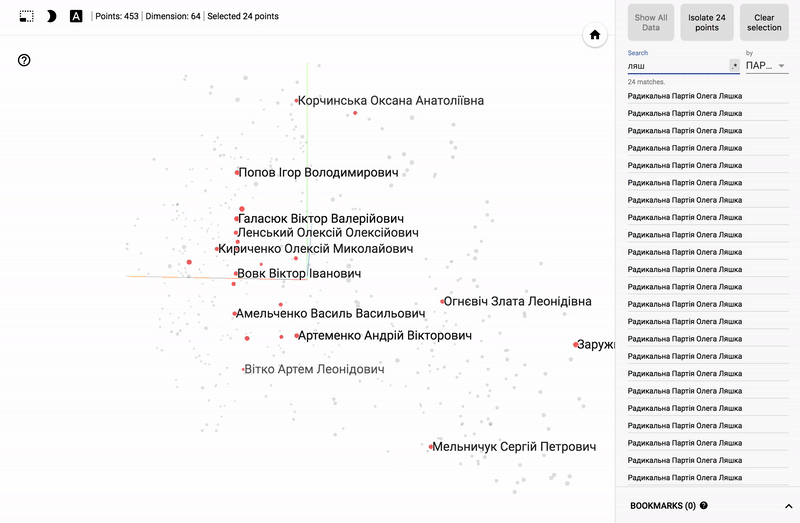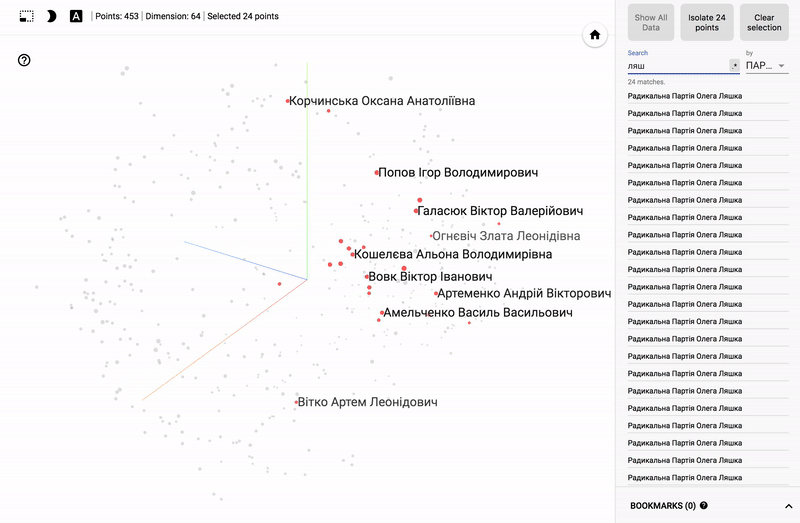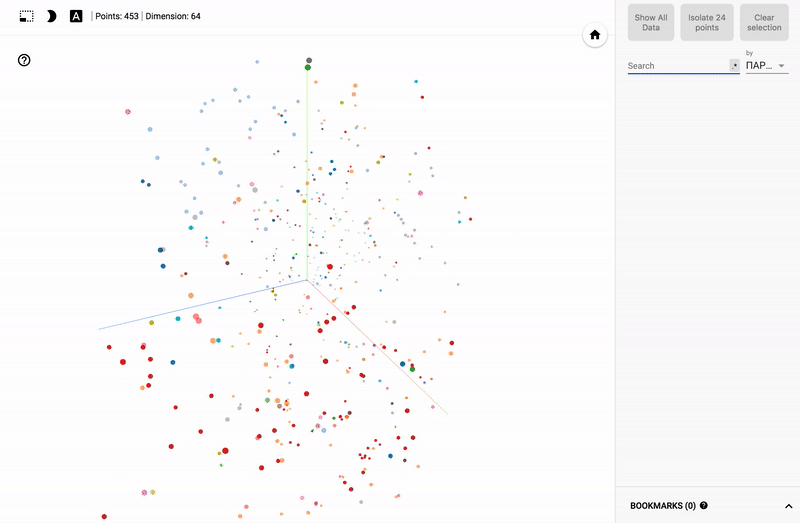
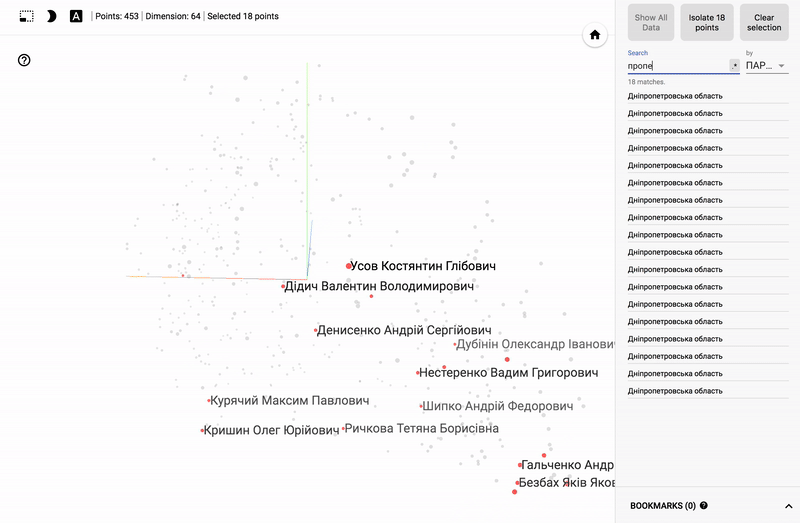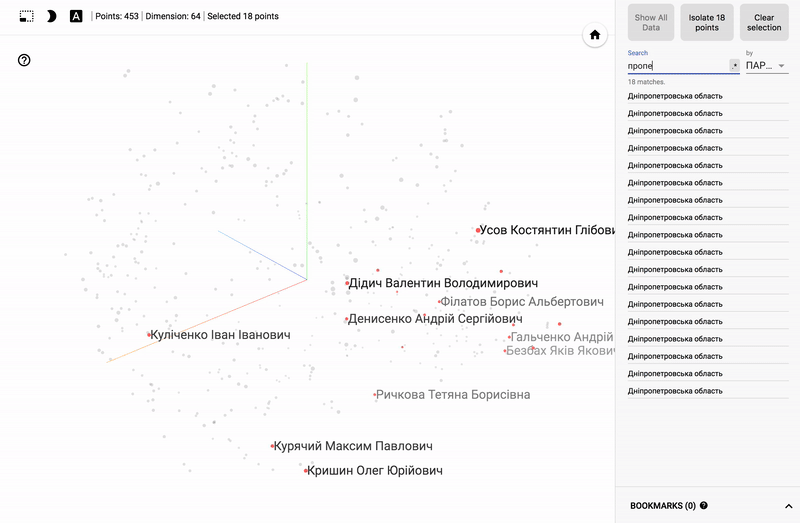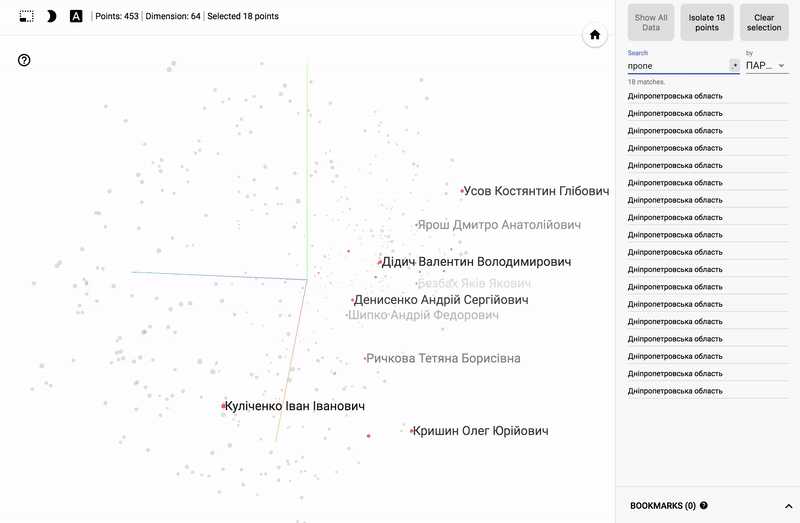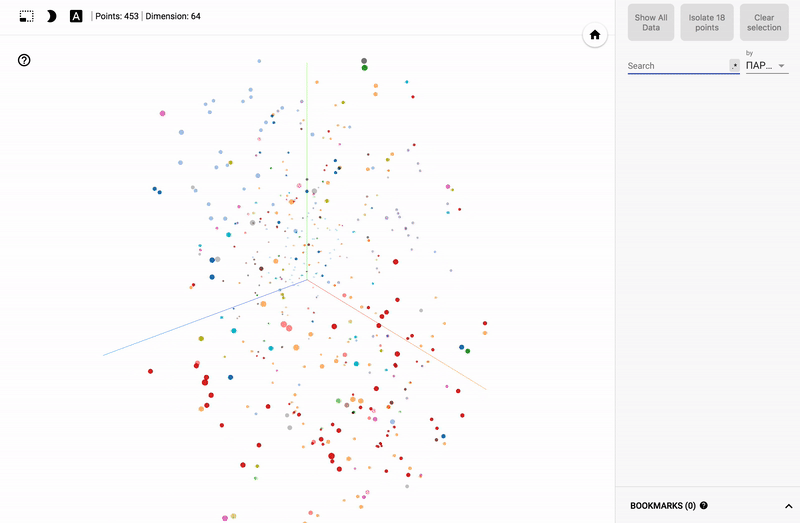
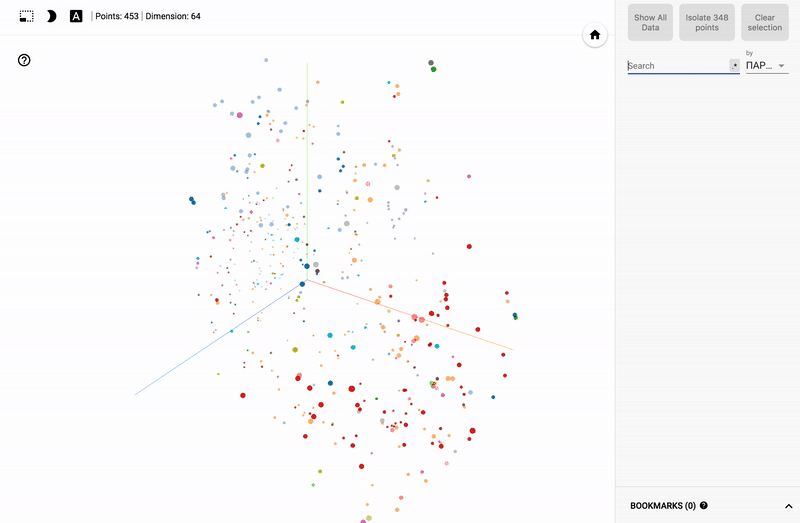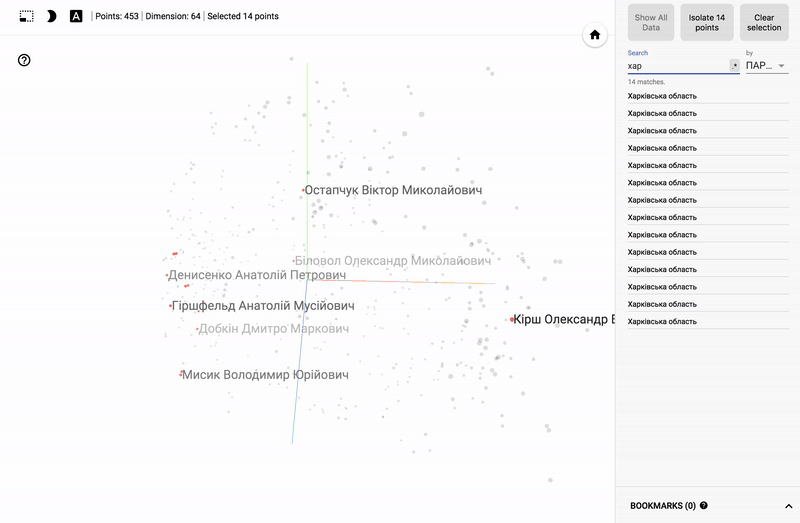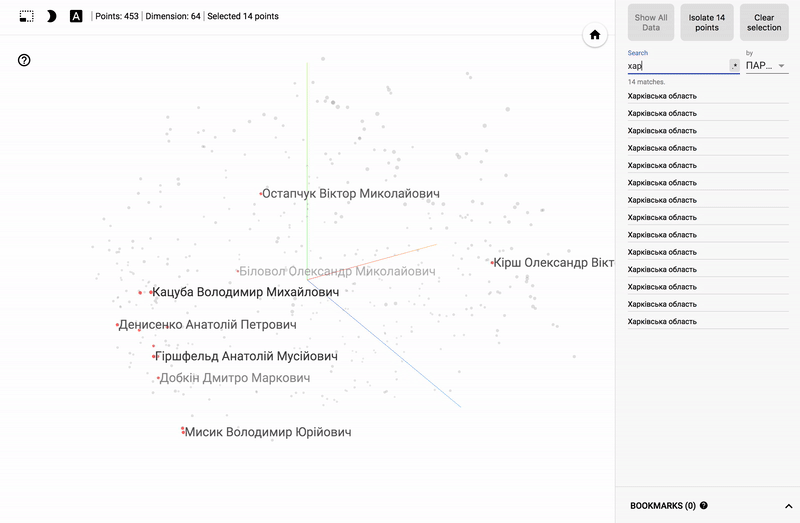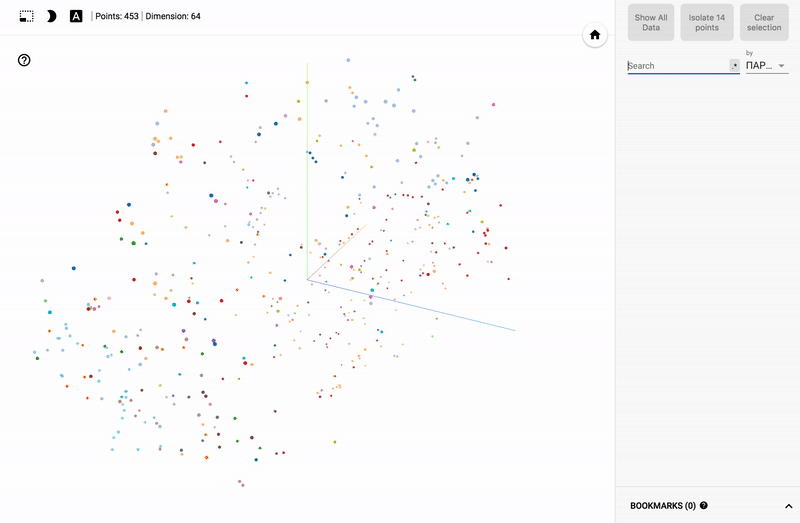
Для тех кто интересуется предметной областью, будет интересно посмотреть на различные срезы, например распределение в голосованиях политиков из различных областей.

• Кучность голосования отдельных партий.
• Распределенность (размазанность) голосования политиков из одной партии.
• Схожесть голосования политиков из различных партий.

Выводы

• Автоэнкодеры — семейство относительно простых алгоритмов, которое дает на удивление быстрый и хороший результат сходимости.
• Автоматическая кластеризация не является ответом на вопрос о природе исходных данных, она требует дополнительной аналитики, но зато дает достаточно быстрый и наглядный вектор, в котором можно начать работать с вашими данными.
• TensorFlow и TensorBoard мощные и быстро развивающиеся инструменты машинного обучения позволяющие решать задачи различной сложности.