Квантово-устойчивый блокчейн

МЕНЮ

Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту

ТЕМЫ

Новости ИИРазработка ИИВнедрение ИИРабота разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика

Авторизация

RSS

RSS новости
В этой статье я расскажу о проблеме безопасности в технологии блокчейн в свете роста производительности квантовых компьютеров, разберу некоторые методы защиты от атак с применением квантового компьютера и о недавно появившемся проекте: Quantum-Resistant Ledger. Как заявляют разработчики, это будет первая в мире платформа, построенная на принципах постквантового шифрования и предназначенная для обеспечения защиты от «квантового удара» на случай быстрого развития этих технологий. Такому удару могут быть подвергнуты платформы, построенные с использованием классических принципов шифрования. Без фундаментальных изменений Bitcoin, Ethereum, Ardor и большинство подобных платформ в недалеком будущем могут оказаться в уязвимости.

Часть 1. Проблема безопасности

Уязвимость

Алгоритм защиты Биткойна и подобных систем построен по принципу асимметричного шифрования с открытым и закрытым ключом. Транзакция подписывается закрытым ключом, а ее истинность проверяется с помощью открытого ключа.

С использованием классических алгоритмов атаки практически невозможно найти закрытый ключ, зная открытый. Системы асимметричного шифрования, такие как RSA и подобные (DSA, DH и пр.), построены на том утверждении, что сложность разложения числа на простые множители растет экспоненциально от размера ключа. Однако, с использованием алгоритма Шора на квантовом компьютере становится возможным за полиномиальное время разложить число на простые множители и, таким образом, найти закрытый ключ, зная открытый.

В 2001 году компания IBM продемонстрировала эту возможность, разложив число 15 на два простых множителя 3 и 5. Для этих целей был использован квантовый компьютер, состоящий из 7 кубитов. С тех пор развитие технологий квантовых вычислений происходит все быстрее.

В 2016 году группа исследователей из Массачусетского технологического института совместно с институтом Иннсбрука выполняет ту же задачу по разложению числа 15, использовав всего 5 кубитов.

В июле 2017 российско-американскими физиками был создан программируемый 51 кубитный компьютер.

В конце октября 2017 Международная исследовательская группа из Сингапурского и Австралийского университетов пришла к выводу, что большинство криптографических протоколов, применяемых в блокчейне, уязвимо к атакам мощного квантового компьютера. В отчете группы приводятся 2 прогноза роста мощности квантового компьютера: оптимистичный и менее оптимистичный. Согласно первому, количество кубит квантового компьютера будет удваиваться каждые 10 месяцев. Менее оптимистичный прогноз говорит об удвоении количества кубит каждые 20 месяцев. На рисунке ниже представлены графики обоих прогнозов.

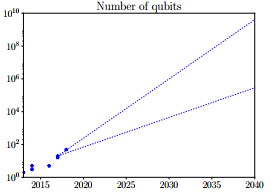
Наиболее уязвимым к атакам квантового компьютера признан алгоритм создания цифровой подписи на основе эллиптических кривых (ECDSA). Таким образом, говорится в отчете группы, Биткойн в его классическом виде может быть взломан уже к 2027 году.

Может, не все так плохо? Публичный ключ не хранится в открытом виде

В конце апреля 2017 года на сайте bitcoin.com выходит статья, призванная ответить на вопрос, стоит ли держателям Биткойна опасаться его взлома с помощью квантового компьютера. В ней говорится, что не смотря на то, что в блокчейне Биткойн применяется асимметричное шифрование, пользователям не стоит опасаться за сохранность своих монет. Открытый ключ не хранится в открытом виде. Так, адреса для передачи монет не являются открытыми ключами, а лишь результатом применения хеш-функции SHA-256. Функция хеширования выполняет одностороннее преобразование и поэтому является устойчивой к атакам квантового компьютера.

Публичный ключ становится известен во время транзакции

Утверждение, что публичный ключ не доступен в открытом виде, не совсем верное. Не вдаваясь в мелкие подробности, разберем на примере Биткойна (BTC), как происходит передача криптовалюты от одного человека к другому.

Пусть Алиса в своем кошельке на одном из Биткойн-адресов имеет 100 mBTC (1000 mBTC = 1 BTC). Она хочет перевести Бобу 1 mBTC. Для этого она указывает Биткойн-адрес Боба, комиссию за перевод и Биткойн-адрес в ее кошельке для получения сдачи. Пусть в качестве комиссии Алиса указала 1 mBTC. Таким образом, из 100 mBTC, имеющихся у Алисы 1 mBTC отправляется Бобу, 1 mBTC уходит в качестве комиссии сети Биткойн и 98 mBTC возвращается в кошелек Алисы.

Теперь разберем, что же происходит на уровне сети Биткойна. У Алисы и Боба есть кошельки, содержащие адреса для хранения монет. Один кошелек может содержать несколько Биткойн-адресов. Адреса генерируются при создании кошельков. Каждому адресу соответствует созданная по алгоритму ECDSA пара ключей: открытый и закрытый. При передаче монет создается транзакция, в которой передается информация о количестве передаваемых Алисой монет, Биткойн-адрес Боба, подпись, выполненная закрытым ключом Алисы, публичный ключ Алисы и некоторые другие данные. Далее транзакция в открытом (нешифрованном) виде отправляется в сеть. Узлы сети, прежде чем принять транзакцию к обработке, проверяют ее подпись используя открытый ключ. В случае достоверности подписи они добавляют информацию о транзакции в блок. Такая операция включения называется подтверждением.

Среднее время генерации блока в сети Биткойн составляет 10 минут. Сеть стремится поддерживать это время постоянным. Прежде чем использовать полученные средства, рекомендуется дождаться 6 подтверждений. Таким образом, Боб, соблюдая правила безопасности, сможет воспользоваться полученными средствами примерно через час после их перевода.

Одной из особенностей передачи монет в сети Биткойн является то, что не возможно передать только часть монет с одного адреса. Монеты всегда передаются всем объемом, находящимся на Биткойн-адресе кошелька, при этом отправителю возвращается сдача. Ее можно получить как на тот адрес, с которого монеты были отправлены, так и на любой другой. Поэтому Алиса должна указать адрес для сдачи. В ряде программного обеспечения, осуществляющего функционирование кошелька, адресом сдачи является адрес отправки.

Комиссия за транзакцию, строго говоря, не является обязательной, но ее отсутствие может надолго отложить выполнение транзакции. Справедливо и обратное утверждение: можно несколько ускорить прохождение транзакции, увеличив размер комиссии. На момент написания статьи (январь 2018) большинство ПО кошельков предлагает указать комиссию в размере 1 mBTC. Есть ряд ресурсов, например, этот, которые позволяют оценить время включения транзакции в блок в зависимости от размера комиссии.

Использование открытого ключа 1 раз

С точки зрения безопасности, лучше всего получать сдачу на новый адрес, открытый ключ которого будет неизвестен сети. В этом случае, пара ключей используется только 1 раз. Однако, согласно статистике по состоянию на декабрь 2017 года около 41,34% адресов используется повторно.

10 минут, чтобы совершить атаку

Тем не менее, вам рано или поздно потребуется воспользоваться средствами, лежащими на новом адресе. Публичный ключ передается в сеть в открытом виде. Пока не пришло подтверждение, средства все еще находятся у отправителя. Если злоумышленник получит открытый ключ во время проведения транзакции, у него будет около 10 минут, чтобы получить закрытый ключ с помощью квантового компьютера и попытаться провести свою транзакцию с того же адреса, задав повышенную комиссию.

Статические адреса более уязвимы

В таких системах как Ethereum, NXT, Ardor и др. открытый ключ становится также известным после первой транзакции. Ситуация усугубляется тем, что токены или смарт-контракты привязаны к статическим адресам, атака на которые может проводиться продолжительное время. Если атака будет успешной, то злоумышленник сможет разрушить всю основанную на этих адресах экономическую систему.

Часть 2. Пути решения

Чем обеспечить устойчивость к атакам квантового компьютера?

В настоящий момент существует несколько основных методов, обеспечивающих защиту от атак квантового компьютера:

  • криптография на основе хешей;
  • криптография на основе кода;
  • криптография на основе матрицы;
  • криптография, основанная на многомерных квадратичных системах;
  • криптография на базе секретного ключа.

При наличии достаточно длинных ключей и соблюдении требований к безопасности данные методы защиты способны противостоять как классическим атакам, так и атакам с использованием квантового компьютера.

Наиболее изученным является использование цифровых подписей на основе хеш-функций.

Как уже было сказано ранее, хеш-функция выполняет одностороннее преобразование сообщения. Сообщение преобразуется в значение хеша фиксированной длины. Использование хеш-функции с одной стороны должно сделать бессмысленным перебор сообщений для получения аналогичного значения хеша. С другой стороны, алгоритм должен быть устойчив к коллизиям: когда 2-м разным сообщениям соответствует одно и то же значение хеш-функции.

Квантовый алгоритм Гровера может быть использован для попытки найти коллизию или выполнить предварительную атаку, чтобы найти исходное сообщение. Для этого потребуется $O(2^{frac{n}{2}})$ операций. Таким образом, для поддержания 128-ми битной безопасности, необходима длина результирующего хеша не менее 256 бит. В качестве такой функции может быть выбрана SHA-256.

Подпись Лэмпорта

Одним из вариантов использования хеш-функции в цифровой подписи является подпись Лэмпорта. Она может быть построена на основе любой односторонней хеш-функции. Криптоустойчивость алгоритма основана на криптоустойчивости применяемых хеш-функций.

Схема подписи
Для сообщения $M$ длиной $m$ генерируются ключи. Сперва парами генерируются закрытые ключи $SK$ длиной $n$, затем, применяя хеш-функцию, из закрытых ключей формируются пары открытых ключей $PK$. Количество пар закрытых и открытых ключей равно количеству бит в исходном сообщении.

При выполнении подписи, побитово читается сообщение, и, в зависимости от значения текущего бита, выбирается один из закрытых ключей соответствующей пары. Выбранные закрытые ключи объединяются в подпись. Далее получившуюся подпись и $m$ пар открытых ключей отправляются адресату.


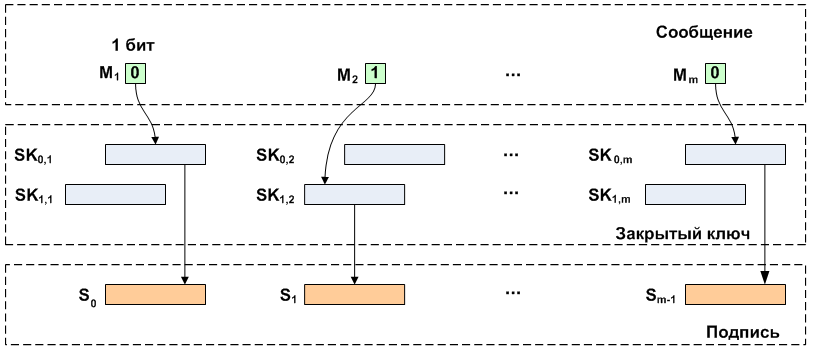
Проверка подписи похожа на процесс ее создания. Подпись разбивается на фрагменты длиной $n$, которые затем преобразуются при помощи той же хеш-функции. Побитово читается сообщение и значением бита выбирается открытый ключ, который сравнивается с полученным значением хеша.

Как правило, перед применением подписи исходное сообщение хешируется для уменьшения его размера. Пусть в качестве хеш-функции выбрана SHA-256, тогда $m = n = 256$. При этом общая длина открытого (как и закрытого) ключа $L_{PK}$ получается равной:

$L_{PK} = n * 2 * m = 256 * 2 * 256 = 128 Кб = 16 КБ.$

Длина подписи $L_S$ составляет:

$L_S = n * m = 64 Кб = 8 КБ.$

Подпись Лэмпорта является одноразовой (остается безопасной только при однократном ее использовании), поскольку при ее выполнении и передаче становится известной половина закрытого ключа. Пусть длина сообщения равна 256 байт и длина хеша равна 256. До того, как Алиса опубликует подпись к сообщению, никто не знает 2 * 256 случайных чисел в секретном ключе. Таким образом, никто не может создать правильный набор из 256 чисел для подписи. После того, как Алиса опубликует подпись, никто все еще не будет знать остальные 256 чисел, и, таким образом, не сможет создать подпись для сообщений, имеющих иной хеш. Тот факт, что подпись Лэмпорта является одноразовой, в сочетании с внушительным суммарным объемом подписи и открытого ключа (24 КБ при длине сообщения в 256 байт и длиной хеша в 256 байт), делает ее использование в публичном блоке транзакций нецелесообразным.

Подпись Винтерница

Существуют и другие алгоритмы одноразовой цифровой подписи. В подписи Винтерница, в отличие от подписи Лэмпорта, исходное сообщение подписывается не побитово, а блочно. Одноразовая подпись Винтерница, как и Лэмпорта, может быть построена на основе любой стойкой криптографической функции.

Схема подписи
Сообщение $M$ длиной $m$ разбивается на фрагменты $M_i$ длиной $w$. Для каждого фрагмента генерируется закрытый ключ $SK$ длины $n$. К каждому закрытому ключу последовательно применяется операция хеширования $2^w-1$ раз (раундов $R$). В результате проведенных операций получаются соответствующие им открытые ключи $PK$ той же длины $n$.


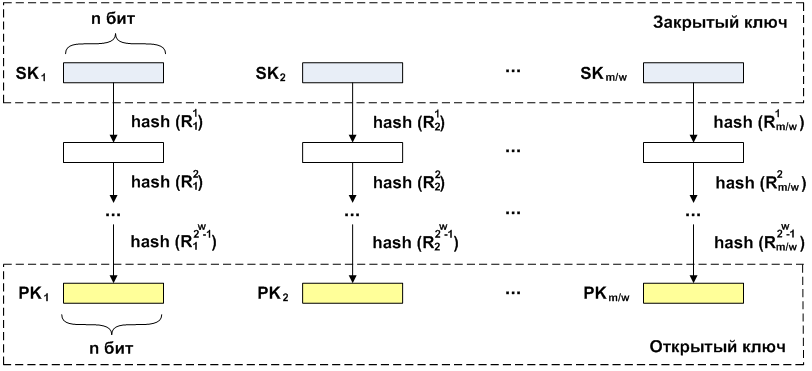
При подписи, как и при генерации публичных ключей, производится итеративное вычисление хеша над закрытыми ключами. Количество повторений в каждом случае зависит от подписываемого сообщения. Как уже говорилось ранее, сообщение разбито на блоки длины $w$. Численное значение этого блока $M_i$ и является количеством итераций, которые необходимо выполнить над закрытыми ключами для получения подписи. Соединение полученных блоков и будет подписью данного сообщения.


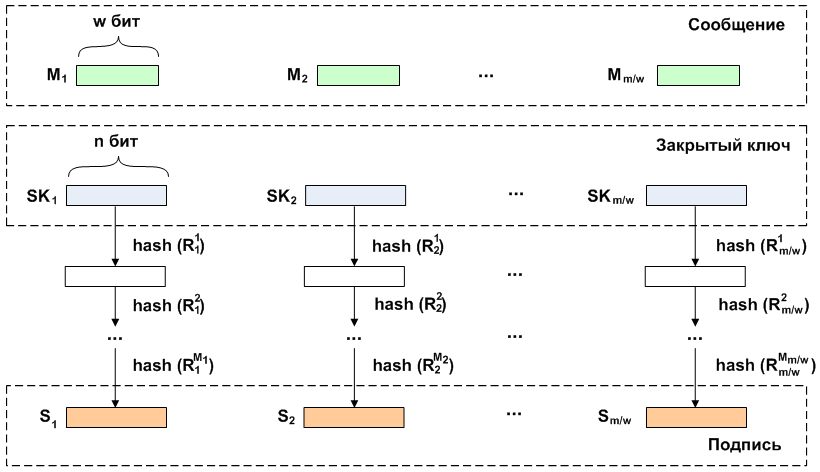
При проверке подписи над фрагментами ее длины $n$ производится итеративное вычисление хеша. Количество раундов $R_i$ применения хеш-функции определяется как разность между количеством итераций для получения открытого ключа и численного значения блока сообщения, т.е. $R_i = 2^w-1 - M_i$ раз. Затем полученные значения сравниваются с соответствующим публичным ключом.

Пример
Проиллюстрирую вышесказанное небольшим примером. Пусть дано сообщение $M$ (в битовом представлении) длины $m$, параметр Винтерница $w$ и некоторая хеш-функция длины $n$:

$M = 11000111:01100111,m = 16,:w = 8,:n = 256.$

Генерируем $m/w = 2$ закрытых ключа на основе генератора псевдослучайных чисел. К каждому закрытому ключу применяем $2^w-1 = 255$ раз хеш-функцию, тем самым получая $2$ открытых ключа, которые объединяются в один общий ключ длины $2 * n = 512$ бит. Далее по каждому блоку сообщения $M$ длины $w$ определяем количество применяемых к закрытому ключу операций хеширования $R_i$. В данном случае это будут значения $11000111_2 = 199_{10}$ и $01100111_2 = 103_{10}$ соответственно. Выполнив операцию хеширования на закрытых ключах получаем подпись длиной $2 * n = 512$ бит.

Для проверки подписи делим ее на части длиной $n$. Над каждой частью производим $R_i=2^w-1 - M_i$ операций хеширования. Т.е. $255 - 199 = 56$ и $255 - 103 = 152$ раза соответственно. Если в результате проведенных операций получается значение совпадающее с открытым ключом, значит, сообщение достоверно.

При использовании SHA-256 в качестве хеш-функции для подписи Винтерница, $m = n = 256$.

Пусть $w = 8$ бит. Тогда полный размер открытого ключа $L_{PK}$ и подписи $L_S$ равны:

$L_{PK} = L_S = m/w * n = 256 / 8 * 256 = 8 Кб = 1 КБ.$

Количество операций вычисления хеша в данном случае равно:

$P = (2^w-1) * m/w = (2^8-1) * 256 / 8 = 8160.$

Для случая с $w = 16$, это значение возрастает до $P = 1048560$.

Размеры открытого ключа и подписи, при тех же параметрах, что и в примере для подписи Лэмпорта, равны 1 КБ. В сумме это меньше, чем в подписи Лэмпорта (24 КБ). Однако, количество операций вычисления хеша при этом составляет 8160. Что, несомненно, очень много. К тому же, при проверке подписи выполняется в среднем половина от этого количества итераций. Это делает данный вариант подписи нецелесообразным для использования в блокчейне. Существует несколько вариантов подписи Винтерница, в том числе с расширением подписи с целью повышения надежности и сокращения количества применений хеш-функции. Их описание выходит за рамки данной статьи. Те, кому интересно, могут посмотреть подробнее здесь. Применение подписи Винтерница на базе отечественной хеш-функции ГОСТ 34.11-12 можно посмотреть здесь.

Дерево Меркла (MSS)

Одноразовые подписи способны обеспечить удовлетворительную криптографическую безопасность, однако, именно их одноразовость может стать серьезной проблемой. Пусть необходимо передать сбережения с одного адреса на другой. При этом получается, что при использовании одноразовых подписей необходимо будет каждый раз переводить весь объем средств, и для проведения каждой транзакции нужен будет новый адрес. С каждой транзакцией нужно будет публиковать новый открытый ключ. Кроме того, сохранение в блокчейне новых транзакций постепенно будет требовать все больше времени на их поиск.

Для решения проблемы расширяют схему подписи за счет проведения нескольких подписываний на основе нескольких пар ключей для каждого адреса. Использование нескольких подписей выполняют на базе двоичного хеш-дерева — дерева Меркла.

Подробнее
Вычисление дерева производится от листьев к корню. Каждый узловой лист дерева вычисляется как хеш от сгенерированного открытого ключа. Остальные узлы вычисляются путем получения хеша от конкатенации (склеивания) дочерних узлов. Таким образом рассчитывается все дерево до корня. Пусть есть 4 пары ключей, дерево Меркла рассчитывается вычислением 7-ми хешей (см. рисунок выше). Особенностью дерева Меркла является то, что существование любого узла или листа может быть криптографически доказано путем вычисления корня. Подпись сообщения создается при помощи закрытого ключа из выбранной пары ключей.
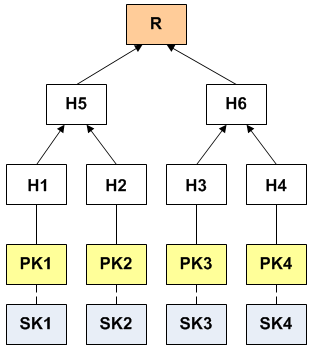
Проверка подписи подразумевает вычисление корня на основе переданных параметров и сравнение с ним как с многоразовым публичным ключом. Этими параметрами являются:

  • подпись;
  • корень;
  • одноразовый ключ, закрытой частью которого было подписано сообщение;
  • хеши из дерева, лежащие на пути следования от выбранного листа к корню.

При использовании одноразовых подписей Меркла или Винтерница нет необходимости передавать отдельно выбранный одноразовый открытый ключ, поскольку его можно получить из подписи сообщения. Достаточно передать его номер, отражающий его положение в дереве. Например, на рисунке выше передаваемыми параметрами будут: подпись, корень, номер листа — 0 (номер листа с ключом $PK1$) и хеши $H2$ и $H6$. При выполнении проверки подписи из нее будет получен открытый ключ $PK1$, соответственно, и хеш $H1$. Хеши $H1$ и $H2$ позволят вычислить $H5$. А хеши $H5$ и $H6$ позволят вычислить корень $R$, который можно будет сравнить со значением переданного корня.
Дерево Меркла, составленное и рассчитанное из открытых ключей, позволяет вместо публикации всего их множества опубликовать лишь корень дерева. Это увеличивает размер подписи за счет включения части дерева в подпись, но дает возможность используя только 1 хеш проверить множество подписей. Так, при глубине дерева $N$ можно подписать $2^N$ сообщений.

Дерево Меркла для ключей на базе алгоритма эллиптических кривых используется в Биткойн и Ethereum, о последнем с рассмотрением дерева Меркла есть отличная статья.

Гипердеревья

Основным недостатком базовой схемы Меркла является то, что количество доступных подписей ограничено, и все пары ключей одноразовых подписей должны быть сгенерированы до вычисления дерева Меркла. Генерация ключей и время подписывания растут экспоненциально относительно высоты дерева. Отсрочить генерацию новых ключей, а также увеличить количество доступных пар возможно при использовании гипердерева.

Подробнее
Гипердерево представляет собой структуру, состоящую из деревьев Меркла. В этой структуре по назначению выделяются 2 типа деревьев: дерево сертификации и дерево подписи. Дереву подписи соответствуют ключи, используемые для подписывания сообщений. Дереву сертификации соответствуют ключи для подписывания корней деревьев подписи. Таким образом, деревья подписи являются дочерними к дереву сертификации (см. рисунок ниже).

Для проверки подписи сообщения в этом случае передаются те же параметры, что и для обычного дерева Меркла, но с обоих деревьев. Таким образом, подпись и ее проверка становятся несколько сложнее, однако появляется возможность гибко расширять структуру. В то время как размер и количество подписей для каждого дополнительного дерева растет линейно, общий объем подписей гипердерева растет экспоненциально. Нет необходимости строить гипердерево симметричным. Всегда можно дополнить его слоями новых деревьев подписи. Таким образом, подписи блока транзакций будут изначально небольшого размера, который будет возрастать по мере увеличения глубины гипердерева.

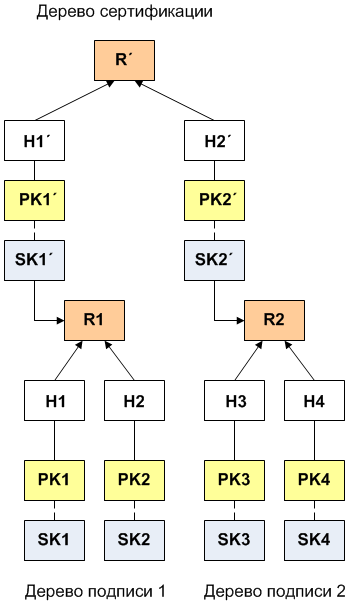
Расширенная структура дерева Меркла (XMSS)

Полное описание схемы выходит далеко за рамки данной статьи, подробнее можно прочесть здесь. Коснусь лишь базовых представлений и характеристик. Схема XMSS как и дерево Меркла позволяет расширять одноразовые подписи. Использование битовой маски с применением исключающего ИЛИ (XOR) дочерних узлов до конкатенации хешей в родительский узел позволяет повысить устойчивость к коллизиям применяемых хеш-функций. Так, при использовании SHA-256 в качестве хеш-функции в сочетании с расширенной схемой Винтерница с параметром безопасности (W-OTS+) позволяет увеличить безопасность с 128 до 196 бит. Согласно Ленстра, 196-битной защиты достаточно, чтобы считать ее безопасной против атаки путем простого перебора до 2169 года. При всех достоинствах схемы XMSS ее основным недостатком является длительное время генерации ключа.

В настоящее время существуют и другие схемы расширения дерева Меркла (GMSS, CMSS), которые в сочетании с алгоритмами одноразовой подписи также могут быть использованы в блокчейне, устойчивом к атакам с применением квантового компьютера.

Часть 3. Реализация идей

Проект квантово-устойчивого блокчена — QRL

Во второй половине 2016 года доктором наук П. Ватерлендом создается группа по разработке блокчейна устойчивого как классическим атакам, так и к атакам с применением квантового компьютера. По результатам разработки теоретической части в конце того же года в открытый доступ выложен главный документ разрабатываемого блокчейна — «белая книга» (white paper). В настоящий момент документ доступен на нескольких языках, включая русский.

Основные характеристики QRL

1. Схема подписи и безопасность
Применяется схема подписи на основе алгоритма расширенной подписи Винтерница (W-OTS+, w = 16, SHA-256) на базе связных структур XMSS. Такой подход позволяет генерировать адреса с возможностью подписи, избегая длительной вычислительной задержки, наблюдаемой при создании гигантских конструкций XMSS. Обеспечивает 196-битную защиту с прогнозируемой безопасностью против атаки путем простого перебора до 2169 года.

2. Алгоритм консенсуса — доказательство работы (proof-of-work)
В первой итерации основной сети анонсирован алгоритм консенсуса proof-of-work.

3. Плавающая комиссия
Бо?льшие размеры транзакций по сравнению с другими блоками цепочки транзакций требуют оплаты для каждой транзакции. По мнению Ватерленда, рынки с искусственной комиссией (например, Биткойн) не нужны и противоречат идеалу открытого блокчейна. Каждая транзакция, если она сопровождается минимальной оплатой, должна быть такой же действительной, как и любая другая. Размер минимальной оплаты, приемлемой для майнеров, должен быть плавающим и устанавливаться рынком. Т.е. узлы (майнеры) должны конкурентно устанавливать нижнюю границу оплаты между собой. Абсолютное минимальное значение будет соблюдаться на уровне протокола. Таким образом, майнеры будут заказывать транзакции из мемпула для включения в блок по своему усмотрению.

4. Динамическое вычисление вознаграждения за блок
Каждый новый созданный блок будет включать в себя первую транзакцию «coinbase», содержащую адрес майнинга, для которого вознаграждение будет определено как сумма вознаграждения за монетную ставку с общей суммой комиссий за транзакции внутри блока.

5. Время нахождения блоков — 1 минута
Время между блоками в сети Биткойн составляет примерно 10 минут. При требуемых 6-ти подтверждениях это дополнительно увеличивает время ожидания завершения транзакции. Более новые схемы блока цепочки транзакций, такие как Ethereum, улучшены в этом аспекте и выигрывают за счет более короткого времени нахождения блока без потери в безопасности или централизации майнеров из-за высокой скорости появления осиротевших/устаревших блоков.

Для QRL это время нахождение блока составляет 1 минуту.

6. Адаптивный размер блока
Во избежание возможных споров было смоделировано готовое адаптивное решение, базирующееся на предложении Bitpay, которое использует для увеличения размера блока множитель $x$ средней величины $y$ последних $z$ блоков. Использование средней величины не позволяет майнерам манипулировать, включая либо пустые, либо переполненные блоки для изменения среднего размера блока. $x$ и $z$ будут тогда жесткими консенсусными правилами для сети, которым придется подчиняться. Таким образом, максимальный размер блока $b$ можно просто вычислить как: $b = xy$.

7. Денежная единица — квант
Базовой единицей валюты является квант. Каждый квант делится на наименьшие элементы. Ниже представлены названия всех элементов в порядке возрастания:
Элемент Значение
Шор $1$
Накамото $10^3$
Бутерин $10^6$
Меркл $10^{10}$
Лэмпорт $10^{13}$
Квант $10^{16}$

Таким образом, каждая транзакция с участием части кванта на самом деле очень большое число единиц Шора. Плата за транзакцию рассчитывается и проводится в единицах Шора.

8. Аккаунты и адреса
Балансы пользователя хранится на аккаунтах. Каждый аккаунт является уникальным многократно используемым адресом блока цепочки транзакций, обозначенным строкой, начинающейся с «Q».

Адрес создается посредством выполнения SHA-256 по корню Меркла самого высокого дерева сертификации XMSS. К этому добавляется четырехбайтная контрольная сумма, образованная из первых четырех байтов двойного хеша SHA-256 корня Меркла, и буквы «Q».

Например, в псевдокоде Python это будет описано следующим образом: 

Q + sha256(merkle root) + sha256(sha256(merkle root))[: 4]

Типичный адрес аккаунта:
Qcea29b1402248d53469e352de662923986f3a94cf0f51522bedd08fb5e64948af479

Каждый аккаунт имеет баланс, деноминированный в квантах, делимый вплоть до единственной единицы Шора. Адреса с каждой транзакцией используют новую пару ключей одноразовой подписи. Счетчик транзакций, называемый nonce, будет увеличиваться с каждой транзакцией, отправленной с аккаунта. Это позволяет кошелькам, которые не хранят всю цепочку блоков, отслеживать их местоположение в схеме подписи гипердерева с сохранением состояния.

Текущее состояние проекта и планы на будущее

После выпуска «белой книги» группа пополнилась несколькими новыми разработчиками и началась работа над воплощением задуманного в жизнь. На сайте проекта появились регулярные отчеты о проделанной работе. И к апрелю 2017 года уже была запущена тестовая сеть блокчейна QRL. Исходный код проекта выложен на Github. Проект активно обсуждается на Bitcointalk и Reddit.

В мае 2017 было проведено ICO в экосистеме Ethereum. Выпущен токен QRL стандарта ERC20. Всего было выпущено 65 млн. токенов. Из них в обращении находится 52 млн. токенов. Постепенно в течение 200 лет будет выпущено еще 40 млн. монет. Таким образом, общий объем эмиссии составит 105 млн. монет. При запуске основной сети эти токены можно будет обменять на QRL монеты в соотношении 1:1. В настоящий момент токены доступны для покупки на таких биржах как Bittrex, Upbit и Liqui. Котировки QRL, согласно сайту coinmarketcap.com, представлены на рисунках ниже.


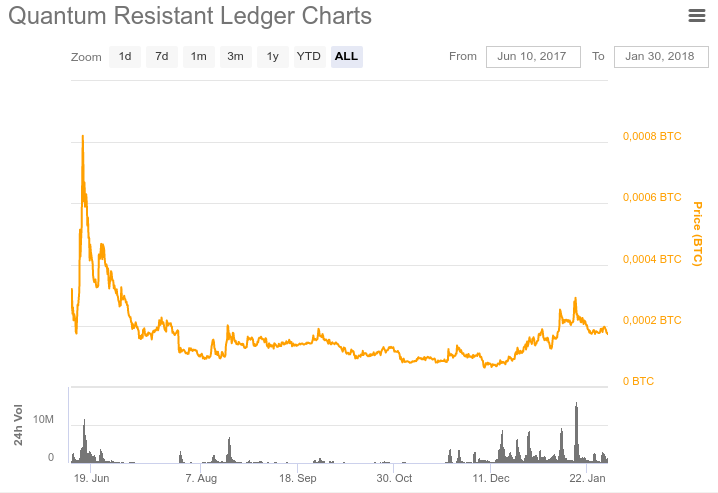
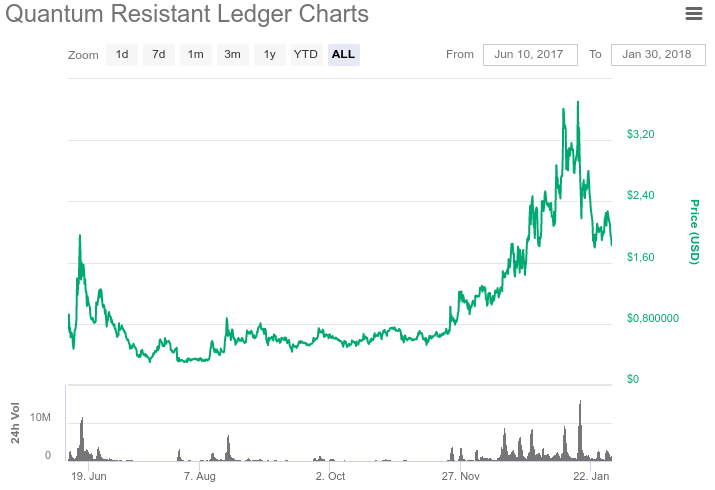Запуск основной сети намечен на февраль-март 2018.

В дальнейшем планируется изменить алгоритм консенсуса с подтверждения работы на подтверждение доли (proof-of-stake). Ожидаемое безопасное время нахождения блоков будет составлять 15-30 секунд.

Заключение

Прогресс квантовых технологий запущен и его уже не остановить. По мере появления все более производительных квантовых машин спектр решаемых ими задач будет непрерывно расти. Взлом существующей криптозащиты, неприспособленной к атакам квантового компьютера, уже давно является одной из центральных тем множества форумов по безопасности.

QRL — первая блокчейн-технология, призванная решить эту проблему. В будущем, конечно, появятся и другие. Какая из них будет наиболее успешной — покажет время.

Благодарности

Автор выражает благодарность kamnik за подготовку значительной части материала и, особенно, за техническую часть, а также SannX за конструктивную критику и правки.

Ссылки

  1. Алгоритм Шора.
  2. Разложение числа 15 на простые множители на квантовом компьютере (IBM).
  3. Разложение числа 15 на простые множители на квантовом компьютере (MIT).
  4. Отчет об экспериментах на 51 кубитном компьютере.
  5. Отчет Международной исследовательской группы об устойчивости Биткойна перед квантовым компьютером.
  6. Использование алгоритма генерации ключей ECDSA в блокчейне Биткойна.
  7. Об устойчивости Биткойна к атакам квантового компьютера.
  8. Подтверждение транзакции в сети Биткойн.
  9. Информация о комиссиях в сети Bitcoin.
  10. Статистика повторного использования Bitcoin-адресов.
  11. Квантовый алгоритм Гровера.
  12. Расширенная подпись Винтерница.
  13. Применение одноразовой подписи Винтерница на базе хеш-функции ГОСТ 34.11-12.
  14. Geektimes об Ethereum.
  15. Схема XMSS.
  16. Ленстра. Выбор размеров криптографических ключей.
  17. GMSS.
  18. CMSS.
  19. Курсы криптовалютных систем.
  20. Ежегодный форум по постквантовой безопасности.


Дополнительный материал

  1. Опасен ли квантовый компьютер для Биткойна.


Проект QRL

  1. Сайт проекта.
  2. Белая книга.
  3. Презентация.
  4. Блог.
  5. Исходный код на GitHub.
  6. Ветка обсуждения на Bitcointalk.

Источник: geektimes.ru

Комментарии: