Книга «Глубокое обучение. Погружение в мир нейронных сетей"
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Искусственный интеллект
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Разработка ИИГолосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
ИИ теория
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Внедрение ИИКомпьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Big data
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Работа разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2018-01-10 16:31
машинное обучение python, архитектура нейронных сетей, нейросети новости

Привет, Хаброжители! Недавно у нас вышла первая русская книга о глубоком обучении от Сергея Николенко, Артура Кадурина и Екатерины Архангельской. Максимум объяснений, минимум кода, серьезный материал о машинном обучении и увлекательное изложение. Сейчас мы рассмотрим раздел «Граф вычислений и дифференцирование на нем» в котором вводятся основополагающее понятие для реализации алгоритмов обучения нейронных сетей.
Если у нас получится представить сложную функцию как композицию более простых, то мы сможем и эффективно вычислить ее производную по любой переменной, что и требуется для градиентного спуска. Самое удобное представление в виде композиции — это представление в виде графа вычислений. Граф вычислений — это граф, узлами которого являются функции (обычно достаточно простые, взятые из заранее фиксированного набора), а ребра связывают функции со своими аргументами.
Это проще увидеть своими глазами, чем формально определять; посмотрите на рис. 2.7, где показаны три графа вычислений для одной и той же функции:
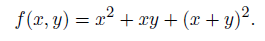
На рис. 2.7, а граф получился совсем прямолинейный, потому что мы разрешили использовать в качестве вершин унарную функцию «возведение в квадрат». 
А на рис. 2.7, б граф чуть более хитрый: явное возведение в квадрат мы заменили обычным умножением. Впрочем, он от этого не сильно увеличился в размерах, потому что в графе вычислений на рис. 2.7, б разрешается по несколько раз переиспользовать результаты предыдущих вычислений и достаточно просто подать один и тот же x два раза на вход функции умножения, чтобы вычислить его квадрат. Для сравнения мы нарисовали на рис. 2.7, в граф той же функции, но без переиспользования; теперь он становится деревом, но в нем приходится повторять целые большие поддеревья, из которых раньше могли выходить сразу несколько путей к корню дерева. В нейронных сетях в качестве базисных, элементарных функций графа вычислений обычно используют функции, из которых получаются нейроны. Например, скалярного произведения векторов 
достаточно для того, чтобы построить любую, даже самую сложную нейронную сеть, составленную из нейронов с функцией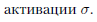 Можно было бы, кстати, выразить скалярное произведение через сложение и умножение, но слишком «мельчить» тут тоже не обязательно: элементарной может служить любая функция, для которой мы сможем легко вычислить ее саму и ее производную по любому аргументу. В частности, прекрасно подойдут любые функции активации нейронов, о которых мы будем подробно говорить в разделе 3.3.
Можно было бы, кстати, выразить скалярное произведение через сложение и умножение, но слишком «мельчить» тут тоже не обязательно: элементарной может служить любая функция, для которой мы сможем легко вычислить ее саму и ее производную по любому аргументу. В частности, прекрасно подойдут любые функции активации нейронов, о которых мы будем подробно говорить в разделе 3.3.
Итак, мы поняли, что многие математические функции, даже с очень сложным поведением, можно представить в виде графа вычислений, где в узлах стоят элементарные функции, из которых, как из кирпичиков, получается сложная композиция, которую мы и хотим подсчитать. Собственно, с помощью такого графа даже с не слишком богатым набором элементарных функций можно приблизить любую функцию сколь угодно точно; об этом мы еще поговорим чуть позже.
А сейчас вернемся к нашему основному предмету — машинному обучению. Как мы уже знаем, цель машинного обучения — подобрать модель (чаще всего здесь имеются в виду веса модели, заданной в параметрическом виде) таким образом, чтобы она лучше всего описывала данные. Под «лучше всего» здесь, как правило, имеется в виду оптимизация некоторой функции ошибки. Обычно она состоит из собственно ошибки на обучающей выборке (функции правдоподобия) и регуляризаторов (априорного распределения), но сейчас нам достаточно просто считать, что есть некая довольно сложная функция, которая дана нам свыше, и мы хотим ее минимизировать. Как мы уже знаем, один из самых простых и универсальных методов оптимизации сложных функций — это градиентный спуск. Мы также недавно выяснили, что один из самых простых и универсальных методов задать сложную функцию — это граф вычислений.
Оказывается, градиентный спуск и граф вычислений буквально созданы друг для друга! Как вас наверняка учили еще в школе (школьная программа вообще содержит много неожиданно глубоких и интересных вещей), чтобы вычислить производную композиции функций (в школе это, вероятно, называлось «производная сложной функции», как будто у слова «сложный» без этого недостаточно много значений), достаточно уметь вычислять производные ее составляющих:

Правило применяется для каждой компоненты отдельно, и результат выходит опять вполне ожидаемый:

Такая матрица частных производных называется матрицей Якоби, а ее определитель — якобианом; они еще не раз нам встретятся. Теперь мы можем подсчитать производные и градиенты любой композиции функций, в том числе векторных, и для этого нужно только уметь вычислять производные каждой компоненты. Для графа все это де факто сводится к простой, но очень мощной идее: если мы знаем граф вычислений и знаем, как брать производную в каждом узле, этого достаточно, чтобы взять производную от всей сложной функции, которую задает граф!

Давайте сначала разберем это на примере: рассмотрим все тот же граф вычислений, который был показан на рис. 2.7. На рис. 2.8, а показаны составляющие граф элементарные функции; мы обозначили каждый узел графа новой буквой, от a до f, и выписали частные производные каждого узла по каждому его входу. Теперь можно подсчитать частную производную 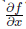 так, как показано на рис. 2.8, б: начинаем считать производные с истоков графа и пользуемся формулой дифференцирования композиции, чтобы подсчитать очередную производную. Например:
так, как показано на рис. 2.8, б: начинаем считать производные с истоков графа и пользуемся формулой дифференцирования композиции, чтобы подсчитать очередную производную. Например:
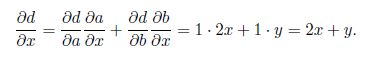
Но можно пойти и в обратном направлении, как показано на рис. 2.8, в. В этом случае мы начинаем с истока, где всегда стоит частная производная  а затем разворачиваем узлы в обратном порядке по формуле дифференцирования сложной функции. Формула окажется здесь применима точно так же; например, в самом нижнем узле мы получим:
а затем разворачиваем узлы в обратном порядке по формуле дифференцирования сложной функции. Формула окажется здесь применима точно так же; например, в самом нижнем узле мы получим:
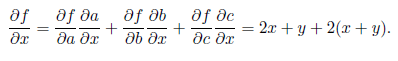
Таким образом, можно применять формулу дифференцирования композиции на графе либо от истоков к стокам, получая частные производные каждого узла по одной и той же переменной 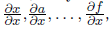
либо от стоков к истокам, получая частные производные стоков по всем промежуточным узлам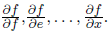 Конечно, на практике для машинного обучения нам нужен скорее второй вариант, чем первый: функция ошибки обычно одна, и нам требуются ее частные производные сразу по многим переменным, в особенности по всем весам, по которым мы хотим вести градиентный спуск.
Конечно, на практике для машинного обучения нам нужен скорее второй вариант, чем первый: функция ошибки обычно одна, и нам требуются ее частные производные сразу по многим переменным, в особенности по всем весам, по которым мы хотим вести градиентный спуск.
В общем виде алгоритм такой: предположим, что нам задан некоторый направленный ациклический граф вычислений G = (V,E), вершинами которого являются функции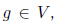 , причем часть вершин соответствует входным переменным x1,... ,xn и не имеет входящих ребер, одна вершина не имеет исходящих ребер и соответствует функции f (весь граф вычисляет эту функцию), а ребра показывают зависимости между функциями, стоящими в узлах. Тогда мы уже знаем, как получить функцию f, стоящую в «последней» вершине графа: для этого достаточно двигаться по ребрам и вычислять каждую функцию в топологическом порядке.
, причем часть вершин соответствует входным переменным x1,... ,xn и не имеет входящих ребер, одна вершина не имеет исходящих ребер и соответствует функции f (весь граф вычисляет эту функцию), а ребра показывают зависимости между функциями, стоящими в узлах. Тогда мы уже знаем, как получить функцию f, стоящую в «последней» вершине графа: для этого достаточно двигаться по ребрам и вычислять каждую функцию в топологическом порядке.
А чтобы узнать частные производные этой функции, достаточно двигаться в обратном направлении. Если нас интересуют частные производные функции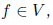 то в полном соответствии с формулами выше мы можем подсчитать
то в полном соответствии с формулами выше мы можем подсчитать  для каждого узла
для каждого узла 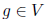 таким образом:
таким образом:

Такой подход называют алгоритмом обратного распространения (backpropagation, backprop, bprop), потому что частные производные считаются в направлении, обратном ребрам графа вычислений. А алгоритм вычисления самой функции или производной по одной переменной, как на рис. 2.8, б, называют алгоритмом прямого распространения (forward propagation, fprop). И последнее важное замечание: обратите внимание, что за все то время, пока мы обсуждали графы вычислений, дифференциалы, градиенты и тому подобное, мы, собственно, ни разу всерьез не упомянули нейронные сети! И действительно, метод вычисления производных/градиентов по графу вычислений сам по себе совершенно никак не связан с нейронными сетями. Это полезно иметь в виду, особенно в делах практических, к которым мы перейдем уже в следующем разделе. Дело в том, что библиотеки Theano и TensorFlow, которые мы будем обсуждать ниже и на которых делается большая часть глубокого обучения, — это, вообще говоря, библиотеки для автоматического дифференцирования, а не для обучения нейронных сетей. Все, что они делают, — позволяют вам задать граф вычислений и чертовски эффективно, с распараллеливанием и переносом на видеокарты, вычисляют градиент по этому графу.
Конечно, «поверх» этих библиотек можно реализовать и собственно библиотеки со стандартными конструкциями нейронных сетей, и это люди тоже постоянно делают (мы ниже будем рассматривать Keras), но важно не забывать базовую идею автоматического дифференцирования. Она может оказаться гораздо более гибкой и богатой, чем просто набор стандартных нейронных конструкций, и может случиться так, что вы будете крайне успешно использовать TensorFlow вовсе не для обучения нейронных сетей.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 20% по купону — Глубокое обучение
Если у нас получится представить сложную функцию как композицию более простых, то мы сможем и эффективно вычислить ее производную по любой переменной, что и требуется для градиентного спуска. Самое удобное представление в виде композиции — это представление в виде графа вычислений. Граф вычислений — это граф, узлами которого являются функции (обычно достаточно простые, взятые из заранее фиксированного набора), а ребра связывают функции со своими аргументами.
Это проще увидеть своими глазами, чем формально определять; посмотрите на рис. 2.7, где показаны три графа вычислений для одной и той же функции:

достаточно для того, чтобы построить любую, даже самую сложную нейронную сеть, составленную из нейронов с функцией
Итак, мы поняли, что многие математические функции, даже с очень сложным поведением, можно представить в виде графа вычислений, где в узлах стоят элементарные функции, из которых, как из кирпичиков, получается сложная композиция, которую мы и хотим подсчитать. Собственно, с помощью такого графа даже с не слишком богатым набором элементарных функций можно приблизить любую функцию сколь угодно точно; об этом мы еще поговорим чуть позже.
А сейчас вернемся к нашему основному предмету — машинному обучению. Как мы уже знаем, цель машинного обучения — подобрать модель (чаще всего здесь имеются в виду веса модели, заданной в параметрическом виде) таким образом, чтобы она лучше всего описывала данные. Под «лучше всего» здесь, как правило, имеется в виду оптимизация некоторой функции ошибки. Обычно она состоит из собственно ошибки на обучающей выборке (функции правдоподобия) и регуляризаторов (априорного распределения), но сейчас нам достаточно просто считать, что есть некая довольно сложная функция, которая дана нам свыше, и мы хотим ее минимизировать. Как мы уже знаем, один из самых простых и универсальных методов оптимизации сложных функций — это градиентный спуск. Мы также недавно выяснили, что один из самых простых и универсальных методов задать сложную функцию — это граф вычислений.
Оказывается, градиентный спуск и граф вычислений буквально созданы друг для друга! Как вас наверняка учили еще в школе (школьная программа вообще содержит много неожиданно глубоких и интересных вещей), чтобы вычислить производную композиции функций (в школе это, вероятно, называлось «производная сложной функции», как будто у слова «сложный» без этого недостаточно много значений), достаточно уметь вычислять производные ее составляющих:



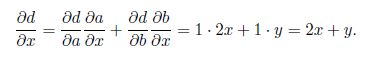
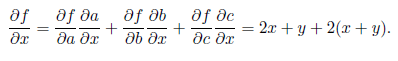
либо от стоков к истокам, получая частные производные стоков по всем промежуточным узлам
В общем виде алгоритм такой: предположим, что нам задан некоторый направленный ациклический граф вычислений G = (V,E), вершинами которого являются функции
А чтобы узнать частные производные этой функции, достаточно двигаться в обратном направлении. Если нас интересуют частные производные функции

Конечно, «поверх» этих библиотек можно реализовать и собственно библиотеки со стандартными конструкциями нейронных сетей, и это люди тоже постоянно делают (мы ниже будем рассматривать Keras), но важно не забывать базовую идею автоматического дифференцирования. Она может оказаться гораздо более гибкой и богатой, чем просто набор стандартных нейронных конструкций, и может случиться так, что вы будете крайне успешно использовать TensorFlow вовсе не для обучения нейронных сетей.
» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок
Для Хаброжителей скидка 20% по купону — Глубокое обучение
Источник: habrahabr.ru