Время — деньги. Как мы учили Яндекс.Такси точно рассчитывать стоимость поездки
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Искусственный интеллект
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Разработка ИИГолосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
ИИ теория
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Внедрение ИИКомпьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Big data
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Работа разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2017-12-22 09:00
ИИ проекты, алгоритмы машинного обучения, разработка беспилотных автомобилей

Любой из нас перед покупкой продукта или услуги старается узнать точную цену. Понятно, что порой случаются истории, когда финальная стоимость сильно превышает запланированную. И если с ремонтом машины или квартиры это уже стало привычным, то в остальных случаях разница между ожиданием и реальностью скорее раздражает.
До недавнего времени стоимость поездки в такси тоже была плавающей. Даже онлайн-сервисы рассчитывали сумму лишь примерно — окончательная стоимость формировалась только в конце пути. Тариф, как правило, включает три компонента: стоимость посадки (иногда с включенными километрами и/или минутами), стоимость километра и стоимость минуты. Конечно, можно было рассчитать примерную цену за поездку и раньше, но в конце она могла измениться из-за того, что, например, по пути водитель задержался в пробке. Понятно, что пассажирам это не всегда нравилось.
Кажется, нет ничего проще, чем использовать данные маршрутизатора в Яндекс.Навигаторе и данные Пробок, чтобы Яндекс.Такси с самого начала рассчитало точную цену, которая не менялась бы по окончании поездки. Но на самом деле на стоимость влияет огромное число факторов, не только тариф. Важно не просто уметь её рассчитывать. С одной стороны, стоимость должна быть привлекательной для пользователя, причём с учётом не только текущей ситуации на дороге, но и, например, пробок, которых на маршруте пока нет, но которые скоро возникнут. С другой, цена должна быть такой, чтобы водители не потеряли в заработке, даже если путь из точки А в точку Б оказался длиннее или дольше, чем планировалось. В этой статье мы расскажем, как решали задачу и как искали сбалансированный алгоритм, выгодный всем участникам платформы Яндекс.Такси.
Адрес — «вершина» виртуального графа — состоит из ребра дорожного графа и направления движения по нему: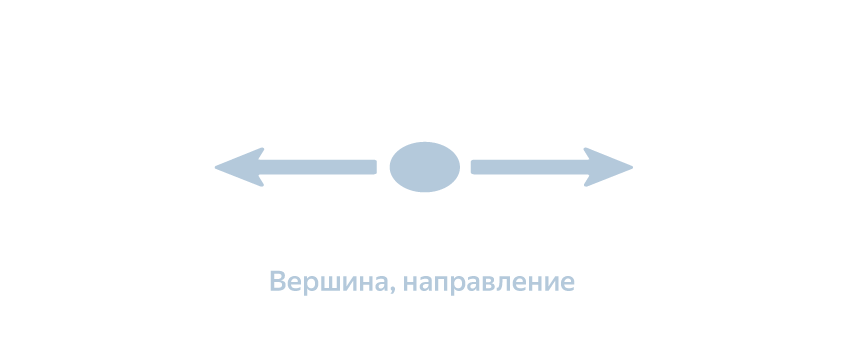
Что происходит, когда вы заказываете поездку в приложении? Мы отправляем запрос в маршрутизатор для того, чтобы найти оптимальный маршрут от точки посадки (А) до пункта назначения (Б), который указан в заказе. Маршрутизатор, в свою очередь, проецирует точку А на граф, чтобы найти её «адрес» — комбинацию ребра и направления. То же самое происходит с точкой Б. И уже здесь проявляется первая особенность системы: процесс определения кратчайшего пути происходит не в оригинальном, «естественном» дорожном графе, а в неком «виртуальном». Его вершинами являются уже не перекрёстки, а те самые «адреса», а рёбрами — не улицы, а «манёвры», то есть переходы из одного «адреса» в другой.
В итоге у нас получилось более 70 разных признаков, влияющих на «стоимость» маршрута, и их количество постоянно растёт, потому что мы постоянно добавляем новые сигналы, которые могут стать признаками и помочь в нашей задаче.
Ещё одна особенность нашего подхода в том, что исходную задачу мы разделили на две: построение маршрута и уточнение времени проезда по нему. Эти модели мы назвали, соответственно, «маршрутной» и «временн?й», и стоит рассказать подробнее, чем они друг от друга отличаются и почему нам нужно именно две модели.
Маршрутная модель служит для выбора оптимального пути из точки А в точку Б из множества вариантов, основываясь на длине маршрута и времени проезда по нему. Загвоздка здесь в том, что маршрутная модель должна выдавать ответ очень и очень быстро, потому что после неё системе нужно время, чтобы эти расчёты использовать в дальнейший цепочки процессов. Скажем, 100 миллисекунд на расчёт 1000 маневров — это слишком много, нужно на порядок меньше. Маршрутная модель должна быть как можно менее затратной в плане вычислений, поэтому она учитывает сокращённый набор признаков. А вот когда у нас уже есть оптимальный маршрут — мы хотим как можно точнее знать время проезда по нему, и здесь мы уже не так связаны быстродействием, можно и 100 миллисекунд себе позволить.
Для этого и существует временн?я модель, единственная задача которой — уточнение времени проезда по уже выбранному пути. Временн?я модель учитывает полный набор признаков для каждого маневра, а также параметры запроса пользователя из приложения: текущее местное время и различные макрохарактеристики маршрута — например, коэффициент перепробега (отношение длины реального маршрута из А в Б к расстоянию между этими точками по прямой). На выходе временн?я модель выдаёт уточнённое время проезда.
Подытожим: наша исходная задача «как наиболее точно построить маршрут и спрогнозировать время поездки по нему» свелась к нескольким шагам. Во-первых, мы перешли от «естественного» графа с вершинами-перекрестками и рёбрами-улицами к «виртуальному» графу, рёбрами которого являются манёвры, то есть переходы из «адреса» в «адрес». Каждый из этих манёвров мы описали набором из более 70 признаков. Во-вторых, для того чтобы оптимизировать работу маршрутизатора, мы решили, что предсказательных моделей будет две: маршрутная, которая быстро, но грубовато, выбирает нужный маршрут из множества возможных, и временн?я, которая уточняет время проезда по оптимальному маршруту. Теперь о том, как эти модели работают.
Первой идеей было просто использовать линейную модель над суммой признаков манёвров по маршруту, а в качестве цели обучения брать реальное время проезда. Этот подход обладает естественной для задачи характеристикой — собственно, линейностью. Действительно, рассчитанное таким образом время для маршрута, состоящего, например, из двух манёвров, равно сумме времён, рассчитанных для каждого из манёвров по отдельности. Не было никаких сложностей и с интерпретацией различных признаков, что всегда приятно: если вес при признаке большой, значит признак значимый.
Тем не менее, несмотря на кучу преимуществ, первые же попытки обучить эту модель оказались огорчающими: результаты были немногим лучше «геометрического времени», потому что мы теряли много информации, заложенной в категориальных (то есть нечисленных) признаках манёвров — например, функциональный класс дорог, форма ребра, уровень дороги над землёй и другие остались «за бортом».
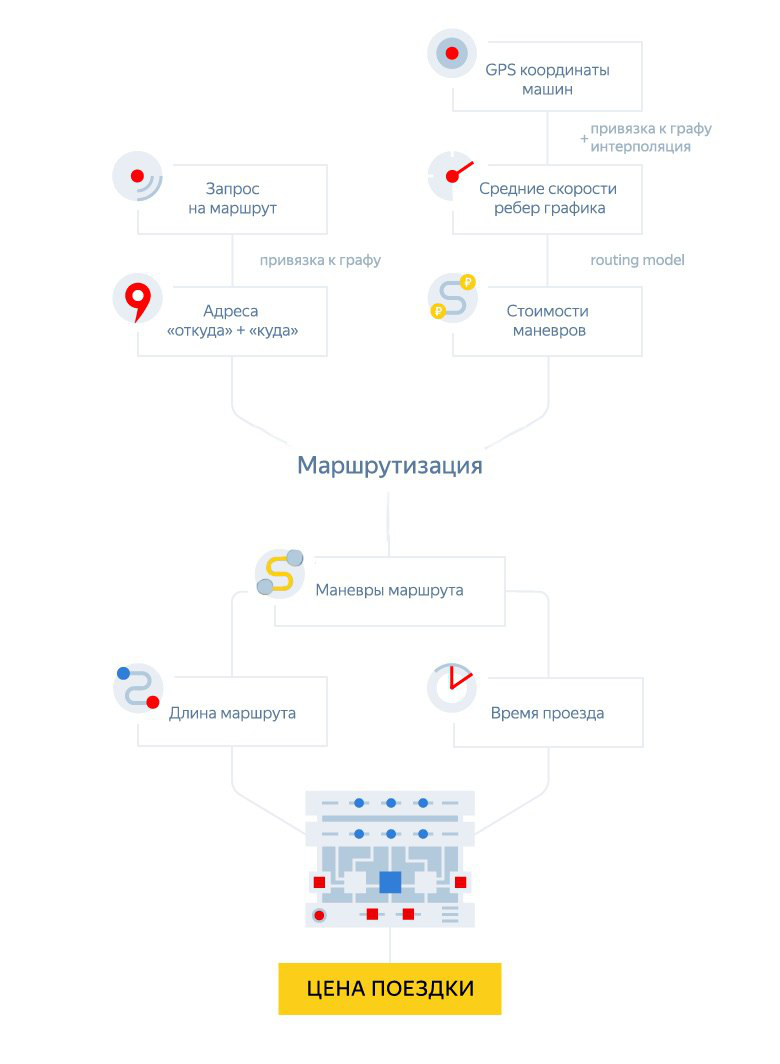
Вот как рассчитывается цена поездки в момент заказа:
Как мы знаем, учёт категориальных переменных — это всегда непростая задача, недаром для этого целый CatBoost придумали. И всё же мы попробовали решить эту проблему, воспользовавшись приёмом, аналогичным N-way-split, который используют в решающих деревьях.
Учтём, что по классификации Народных Карт дороги делятся на 9 функциональных классов, а ещё бывает 5 видов конструктивных особенностей: две проезжие части, круговое движение, съезд, дублёр, разворот. К тому же на дороге или есть светофор или его нет — это ещё два значения. Итого имеем 9х5х2=90 комбинаций. Теперь для каждой такой комбинации категориальных признаков будем отдельно учитывать остальные признаки, то есть исходно поделим нашу выборку на 90 независимых фрагментов. Из-за такого дробления мы в общей сложности получили несколько тысяч признаков, потому что по сути рассматривали каждый из них 90 раз — для каждой отдельной комбинации. Даже с учётом больших обучающих выборок такая “мультипликация” привела к тому, что модель стала быстро переобучаться. Частично эту проблему удалось решить за счет L1-регуляризации (она, в отличие от L2, умеет нивелировать влияние признаков, обнуляя веса при них), но в итоге по совокупности проблем подход пришлось признать тупиковым. Правда, были и хорошие новости: такую временн?ю модель уже можно было использовать в качестве маршрутной, потому что она обладала линейностью по отдельным манёврам, а значит, мы двигались в нужном направлении.
И всё-таки, проблема оставалась: как справиться с таким количеством признаков? У Яндекса есть Матрикснет — алгоритм машинного обучения, основанный на градиентом бустинге решающих деревьев, который успешно справляется с сотнями и даже тысячами признаков. Для начала мы попробовали подход «в лоб» и обучили Матрикснет на парах «маршрут — реальное время проезда». Такой метод сразу же дал хороший результат, а дальнейшая работа по наращиванию количества признаков и тонкая настройка гиперпараметров алгоритма помогли получить ощутимый прирост в качестве прогнозирования. Но, несмотря на мгновенный «выхлоп», обусловленный попросту мощью Матрикснета, были и недостатки:
То есть для наших задач использование Матрикснета «в лоб» не подошло. В итоге мы остались с двумя разными моделями, каждая из которых была по своему хороша, но и чем-то плоха. В такой парадигме — линейная (и грозившая переобучиться) маршрутная модель и временн?я модель на основе Матрикснет — мы пытались какое-то время развиваться, однако душе хотелось какого-то универсального решения. И оно нашлось.
После некоторых мук подбора правильного темпа обучения и количества деревьев удалось получить модель, которая почти не проигрывала «чистому» Матрикснету по качеству, зато обладала линейностью. Это позволяло использовать её в качестве маршрутной модели, а также открывало доступ к лёгкому использованию категориальных признаков за счёт их оцифровки и использования CatBoost.
До недавнего времени стоимость поездки в такси тоже была плавающей. Даже онлайн-сервисы рассчитывали сумму лишь примерно — окончательная стоимость формировалась только в конце пути. Тариф, как правило, включает три компонента: стоимость посадки (иногда с включенными километрами и/или минутами), стоимость километра и стоимость минуты. Конечно, можно было рассчитать примерную цену за поездку и раньше, но в конце она могла измениться из-за того, что, например, по пути водитель задержался в пробке. Понятно, что пассажирам это не всегда нравилось.
Кажется, нет ничего проще, чем использовать данные маршрутизатора в Яндекс.Навигаторе и данные Пробок, чтобы Яндекс.Такси с самого начала рассчитало точную цену, которая не менялась бы по окончании поездки. Но на самом деле на стоимость влияет огромное число факторов, не только тариф. Важно не просто уметь её рассчитывать. С одной стороны, стоимость должна быть привлекательной для пользователя, причём с учётом не только текущей ситуации на дороге, но и, например, пробок, которых на маршруте пока нет, но которые скоро возникнут. С другой, цена должна быть такой, чтобы водители не потеряли в заработке, даже если путь из точки А в точку Б оказался длиннее или дольше, чем планировалось. В этой статье мы расскажем, как решали задачу и как искали сбалансированный алгоритм, выгодный всем участникам платформы Яндекс.Такси.
Маршрут и время
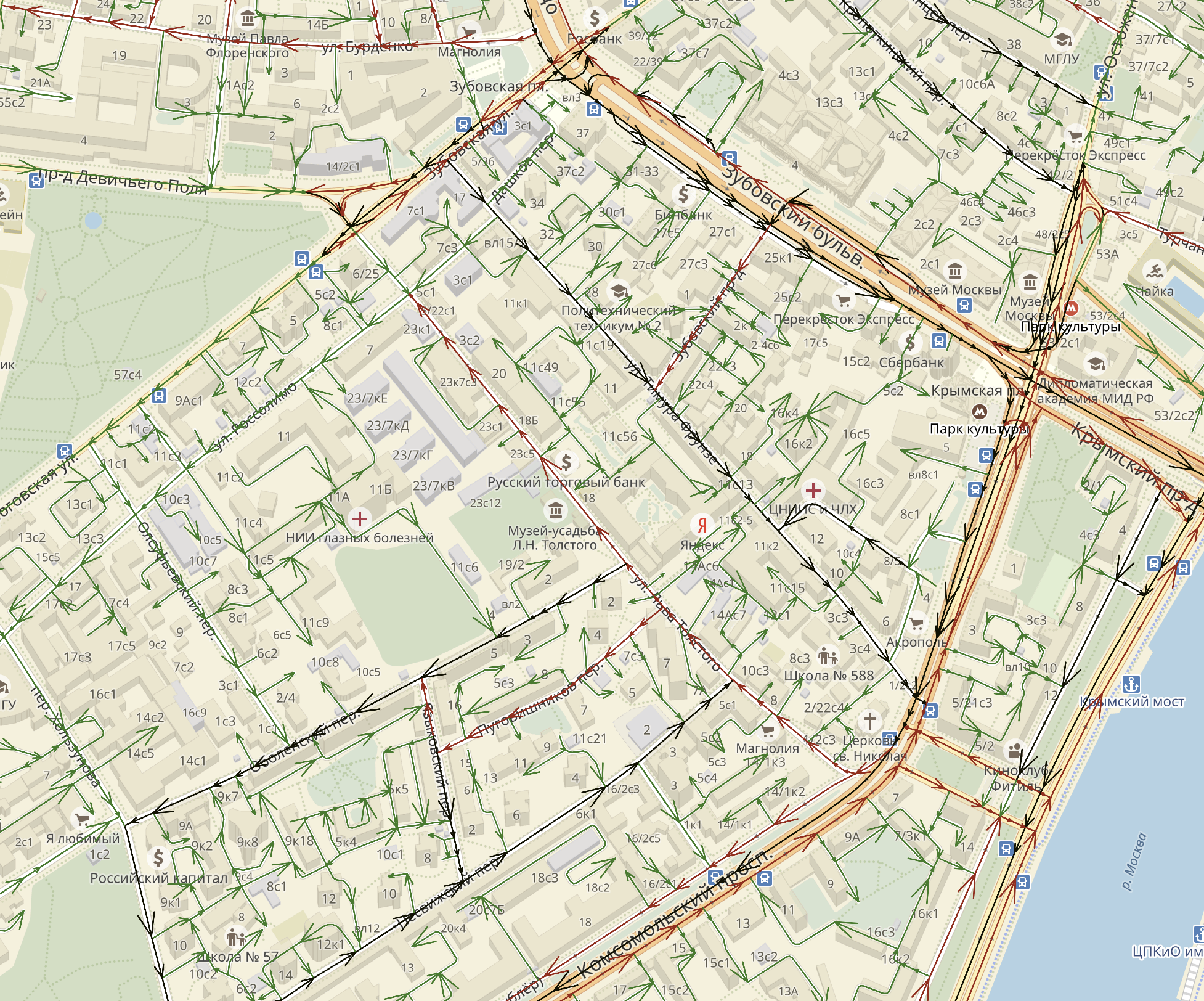
Для того чтобы иметь возможность рассчитывать сбалансированную стоимость поездки, мы должны были научиться точно прогнозировать длину и продолжительность маршрута. Давайте разберёмся, как вообще исходно работает наш маршрутизатор. Это довольно сложная система, которая строит маршрут из одного пункта в другой на основе другой системы попроще — дорожного графа. Граф выглядит так же естественно, как вы наверняка себе его и представляете: каждая дорога соответствует одному или нескольким рёбрам, а перекрёстки и разветвления дорог находятся в вершинах. Этот граф — направленный (так как дороги — это тоже штука направленная).
Так выглядит дорожный граф в районе московского офиса Яндекса
Наиболее важная характеристика рёбер графа — средняя скорость движения по ним в данный момент. Она зависит от текущей дорожной обстановки и от правил дорожного движения (например, ограничений скорости). Каждую секунду мы получаем десятки тысяч обезличенных сигналов — GPS-треков — от пользователей геосервисов Яндекса, агрегируем их, а далее за счёт фильтрации и интерполяции делаем сигнал более качественным и менее шумным. На финальной стадии вычисляем текущую скорость ребра в режиме реального времени (подробнее о том, как работают Пробки можно прочитать здесь).Адрес — «вершина» виртуального графа — состоит из ребра дорожного графа и направления движения по нему:

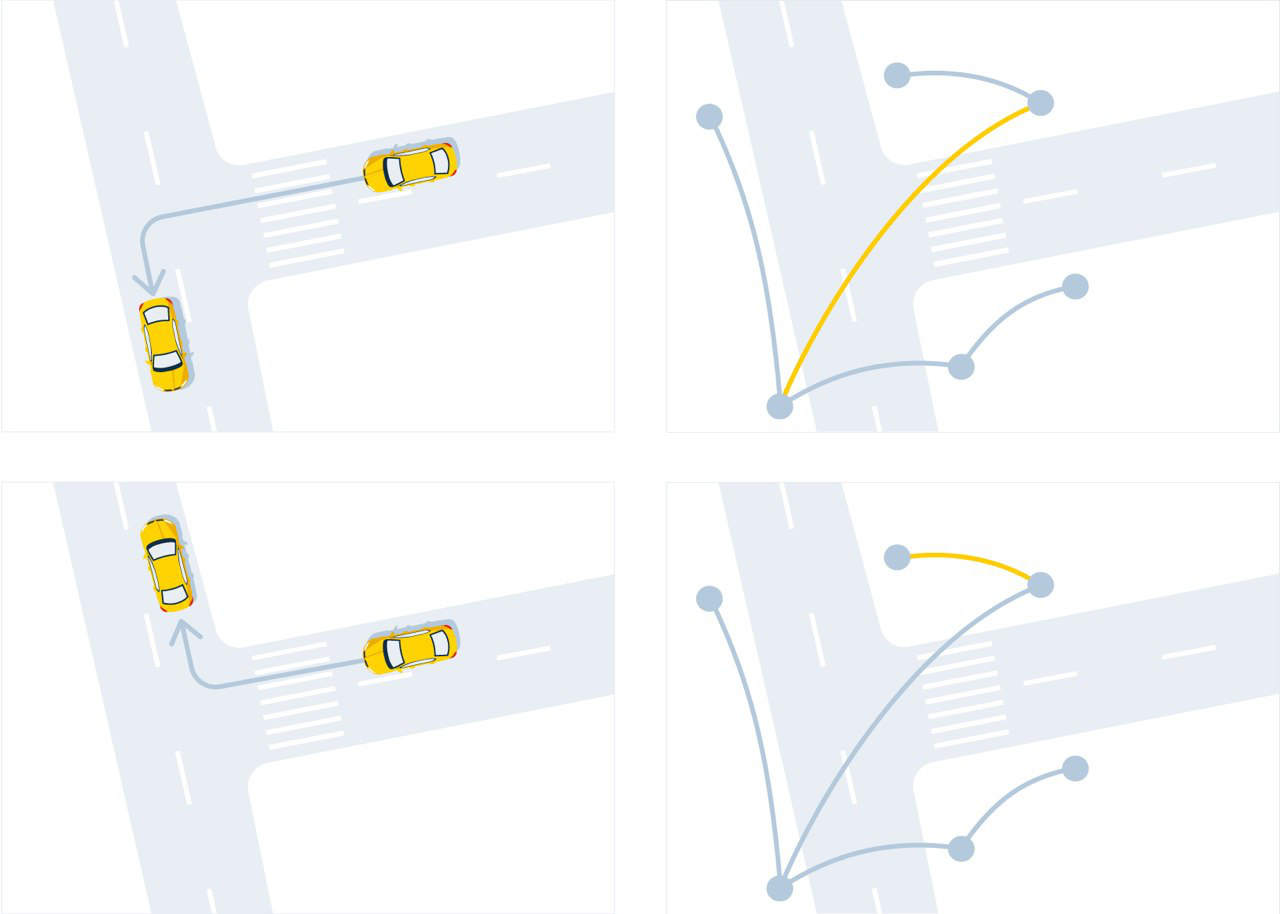
Что происходит, когда вы заказываете поездку в приложении? Мы отправляем запрос в маршрутизатор для того, чтобы найти оптимальный маршрут от точки посадки (А) до пункта назначения (Б), который указан в заказе. Маршрутизатор, в свою очередь, проецирует точку А на граф, чтобы найти её «адрес» — комбинацию ребра и направления. То же самое происходит с точкой Б. И уже здесь проявляется первая особенность системы: процесс определения кратчайшего пути происходит не в оригинальном, «естественном» дорожном графе, а в неком «виртуальном». Его вершинами являются уже не перекрёстки, а те самые «адреса», а рёбрами — не улицы, а «манёвры», то есть переходы из одного «адреса» в другой.

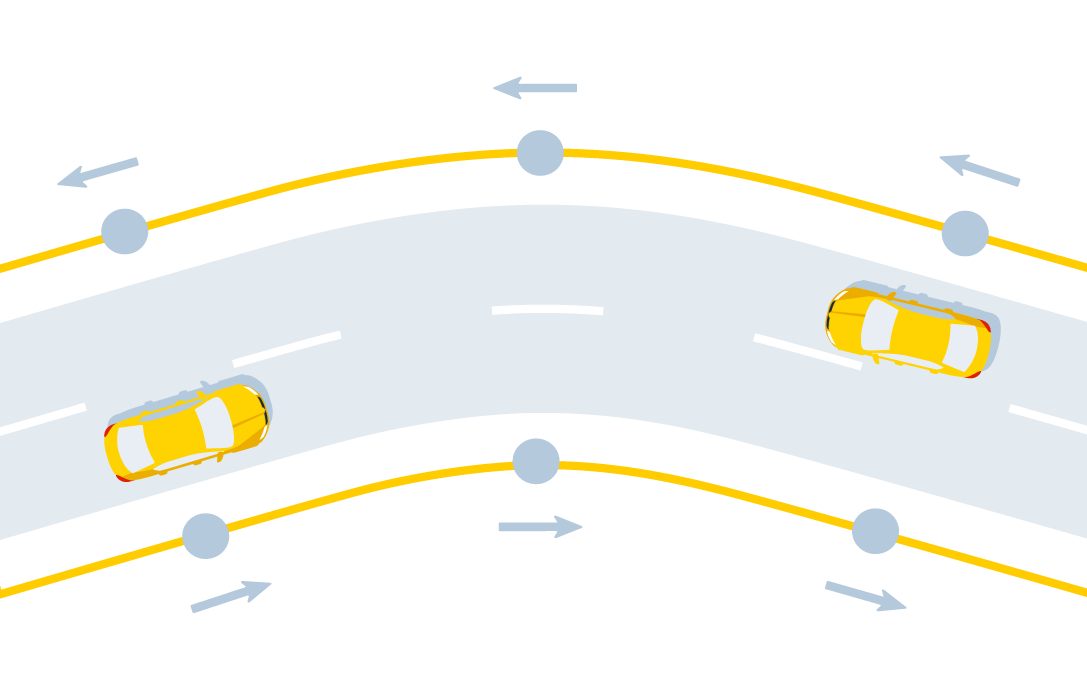
Представление одной и той же траектории движения в дорожном (слева) и в виртуальном (справа) графах

Движение по прямой тоже может состоять из маневров виртуального графа: для удобства длинная дорога при оцифровке превращается в несколько ребер
Как мы помним, наша задача — найти оптимальный маршрут, при этом, разумеется, конечному «физическому» маршруту будет совершенно всё равно, построили ли мы его в «естественном» графе или «виртуальном». Но для начала нужно определиться, что такое оптимальность. С одной стороны, очевидно, что в городе это самый быстрый путь из А в Б. С другой стороны, иногда сложный маршрут по маленьким улицам и в обход больших магистралей хоть и даёт экономию в 2 минуты, но, за счёт большого количества поворотов оказывается значительно «дороже» для автомобилиста. Поэтому для начала мы определили функцию, которая задает «стоимость» манёвра и решили оптимизировать её с помощью машинного обучения. Простейшим примером такой функции может быть длина рёбер, составляющих манёвр, разделённая на среднюю скорость движения по этим рёбрам, — так называемое «геометрическое время». Эта метрика хороша своей простотой, однако она зачастую не учитывает целый ряд особенностей конкретного манёвра. Возьмём для примера поворот налево. Очевидно, что совершить его со второстепенной дороги на регулируемом перекрестке — это совсем не то же самое, что свернуть на съезд, двигаясь по магистрали. Особенности каждой отдельной ситуации могут значительно увеличить время совершения всего манёвра, и чтобы их учесть, мы решили описать каждый манёвр набором признаков: длина составляющих его рёбер, геометрическое время проезда, функциональные классы дорог, наличие выделенной полосы общественного транспорта и так далее. Здесь же естественным образом возникли «признаки будущего»: например, мы можем заранее рассчитать время на прохождение манёвра с учётом пробок, которые возникнут к тому моменту, когда мы к этому манёвру приблизимся.В итоге у нас получилось более 70 разных признаков, влияющих на «стоимость» маршрута, и их количество постоянно растёт, потому что мы постоянно добавляем новые сигналы, которые могут стать признаками и помочь в нашей задаче.
Ещё одна особенность нашего подхода в том, что исходную задачу мы разделили на две: построение маршрута и уточнение времени проезда по нему. Эти модели мы назвали, соответственно, «маршрутной» и «временн?й», и стоит рассказать подробнее, чем они друг от друга отличаются и почему нам нужно именно две модели.
Маршрутная модель служит для выбора оптимального пути из точки А в точку Б из множества вариантов, основываясь на длине маршрута и времени проезда по нему. Загвоздка здесь в том, что маршрутная модель должна выдавать ответ очень и очень быстро, потому что после неё системе нужно время, чтобы эти расчёты использовать в дальнейший цепочки процессов. Скажем, 100 миллисекунд на расчёт 1000 маневров — это слишком много, нужно на порядок меньше. Маршрутная модель должна быть как можно менее затратной в плане вычислений, поэтому она учитывает сокращённый набор признаков. А вот когда у нас уже есть оптимальный маршрут — мы хотим как можно точнее знать время проезда по нему, и здесь мы уже не так связаны быстродействием, можно и 100 миллисекунд себе позволить.
Для этого и существует временн?я модель, единственная задача которой — уточнение времени проезда по уже выбранному пути. Временн?я модель учитывает полный набор признаков для каждого маневра, а также параметры запроса пользователя из приложения: текущее местное время и различные макрохарактеристики маршрута — например, коэффициент перепробега (отношение длины реального маршрута из А в Б к расстоянию между этими точками по прямой). На выходе временн?я модель выдаёт уточнённое время проезда.
Подытожим: наша исходная задача «как наиболее точно построить маршрут и спрогнозировать время поездки по нему» свелась к нескольким шагам. Во-первых, мы перешли от «естественного» графа с вершинами-перекрестками и рёбрами-улицами к «виртуальному» графу, рёбрами которого являются манёвры, то есть переходы из «адреса» в «адрес». Каждый из этих манёвров мы описали набором из более 70 признаков. Во-вторых, для того чтобы оптимизировать работу маршрутизатора, мы решили, что предсказательных моделей будет две: маршрутная, которая быстро, но грубовато, выбирает нужный маршрут из множества возможных, и временн?я, которая уточняет время проезда по оптимальному маршруту. Теперь о том, как эти модели работают.
Модели
Несмотря на то, что и маршрутная, и временн?я модели сильно отличаются друг от друга, у них, по сути, схожая задача — рассчитать время проезда по маршруту. Ключевое отличие — в сложности используемых вычислений, то есть в количественном, а не качественном факторе. При этом, раз у моделей одинаковая задача, то и подход с точки зрения их обучения одинаковый. Мы можем взять только одну модель — временн?ю, — а затем убрать из нее «всё лишнее» (например, лишние признаки) и получить таким образом более легковесную маршрутную модель. Такой подход оказался выигрышным не только из-за того, что он унифицировал метод машинного обучения, но и по другим причинам, в том числе и потому, что обучение временн?й модели — это задача классическая, что называется, «из учебника». У нас есть огромная база историй поездок, то есть очень много пар «маршрут — время», которую можно использовать в качестве выборки для какого-нибудь метода машинного обучения. Маршрутную модель обучить сложнее, потому что мы не можем заставить всех водителей кататься по всем вариантам маршрутов из точки А в точку Б, чтобы сравнить, какой из них быстрее. В итоге на первом этапе мы сконцентрировались именно на обучении временн?й модели.Первой идеей было просто использовать линейную модель над суммой признаков манёвров по маршруту, а в качестве цели обучения брать реальное время проезда. Этот подход обладает естественной для задачи характеристикой — собственно, линейностью. Действительно, рассчитанное таким образом время для маршрута, состоящего, например, из двух манёвров, равно сумме времён, рассчитанных для каждого из манёвров по отдельности. Не было никаких сложностей и с интерпретацией различных признаков, что всегда приятно: если вес при признаке большой, значит признак значимый.
Тем не менее, несмотря на кучу преимуществ, первые же попытки обучить эту модель оказались огорчающими: результаты были немногим лучше «геометрического времени», потому что мы теряли много информации, заложенной в категориальных (то есть нечисленных) признаках манёвров — например, функциональный класс дорог, форма ребра, уровень дороги над землёй и другие остались «за бортом».
Вот как рассчитывается цена поездки в момент заказа:

Как мы знаем, учёт категориальных переменных — это всегда непростая задача, недаром для этого целый CatBoost придумали. И всё же мы попробовали решить эту проблему, воспользовавшись приёмом, аналогичным N-way-split, который используют в решающих деревьях.
Учтём, что по классификации Народных Карт дороги делятся на 9 функциональных классов, а ещё бывает 5 видов конструктивных особенностей: две проезжие части, круговое движение, съезд, дублёр, разворот. К тому же на дороге или есть светофор или его нет — это ещё два значения. Итого имеем 9х5х2=90 комбинаций. Теперь для каждой такой комбинации категориальных признаков будем отдельно учитывать остальные признаки, то есть исходно поделим нашу выборку на 90 независимых фрагментов. Из-за такого дробления мы в общей сложности получили несколько тысяч признаков, потому что по сути рассматривали каждый из них 90 раз — для каждой отдельной комбинации. Даже с учётом больших обучающих выборок такая “мультипликация” привела к тому, что модель стала быстро переобучаться. Частично эту проблему удалось решить за счет L1-регуляризации (она, в отличие от L2, умеет нивелировать влияние признаков, обнуляя веса при них), но в итоге по совокупности проблем подход пришлось признать тупиковым. Правда, были и хорошие новости: такую временн?ю модель уже можно было использовать в качестве маршрутной, потому что она обладала линейностью по отдельным манёврам, а значит, мы двигались в нужном направлении.
И всё-таки, проблема оставалась: как справиться с таким количеством признаков? У Яндекса есть Матрикснет — алгоритм машинного обучения, основанный на градиентом бустинге решающих деревьев, который успешно справляется с сотнями и даже тысячами признаков. Для начала мы попробовали подход «в лоб» и обучили Матрикснет на парах «маршрут — реальное время проезда». Такой метод сразу же дал хороший результат, а дальнейшая работа по наращиванию количества признаков и тонкая настройка гиперпараметров алгоритма помогли получить ощутимый прирост в качестве прогнозирования. Но, несмотря на мгновенный «выхлоп», обусловленный попросту мощью Матрикснета, были и недостатки:
- Стало сложно интерпретировать результаты, потому что в случае градиентного бустинга над деревьями мы работаем, по сути, с чёрным ящиком. Уже нельзя просто трактовать различные признаки в зависимости от их весов.
- Из модели пропала линейность — нельзя разбить маршрут на 2 кусочка, применить к ним модель, сложить и получить то же самое число, что и для маршрута целиком.
- Такую модель не получалось использовать в качестве маршрутной, ведь мы обучали ее на маршрутах целиком, а не на отдельных маневрах.
То есть для наших задач использование Матрикснета «в лоб» не подошло. В итоге мы остались с двумя разными моделями, каждая из которых была по своему хороша, но и чем-то плоха. В такой парадигме — линейная (и грозившая переобучиться) маршрутная модель и временн?я модель на основе Матрикснет — мы пытались какое-то время развиваться, однако душе хотелось какого-то универсального решения. И оно нашлось.
«Линейный Матрикснет»
Как это обычно бывает, идея, когда она уже пришла в голову, оказалось до слёз простой: применить Матрикснет к отдельным манёврам, а не ко всему маршруту, а в качестве функции ошибки брать следующую разность: сумма значений времени по маневрам маршрута минус целевое время проезда. где T — Цель, f — признаки, F — оптимизируемая функция. Хотя такая функция очень напоминает задачу ранжирования в поиске (оптимизация поисковой выдачи как единого целого), в нужной форме такого инструмента Матрикснета среди готовых не было, поэтому нам пришлось реализовать его самостоятельно.После некоторых мук подбора правильного темпа обучения и количества деревьев удалось получить модель, которая почти не проигрывала «чистому» Матрикснету по качеству, зато обладала линейностью. Это позволяло использовать её в качестве маршрутной модели, а также открывало доступ к лёгкому использованию категориальных признаков за счёт их оцифровки и использования CatBoost.
Результаты
Вся эта история заняла достаточно много времени, однако в конечном счёте мы получили модель, которая одновременно удовлетворяла всем требованиям по быстродействию и давала необходимую точность при оценке времени. Именно эта последняя характеристика дала возможность точно рассчитывать стоимость поездки на такси заранее, и не менять её по окончании пути. Последний вопрос — какие результаты мы получили, есть ли с чем сравнить? Разумеется, полный ответ потребовал бы обсуждения множества факторов и достаточно серьёзной аналитики. Но какие-то совсем простые оценки мы можем дать.

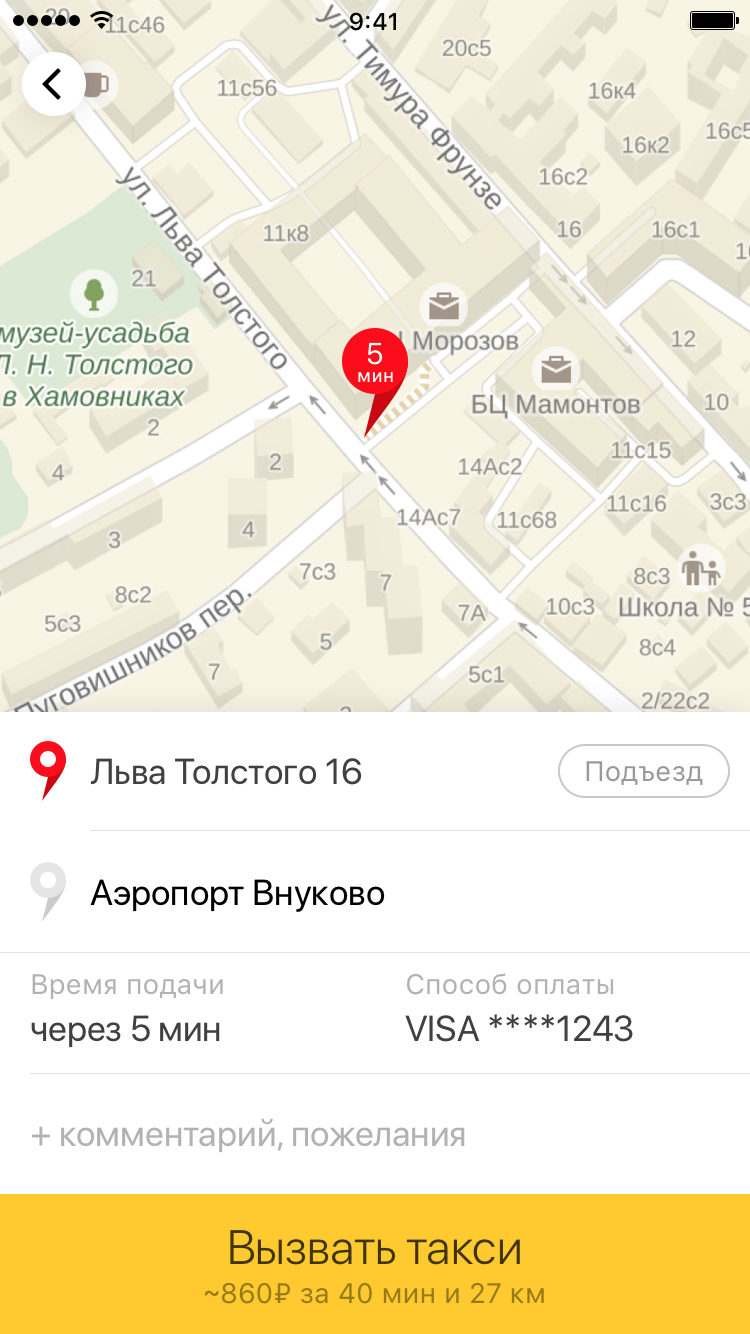
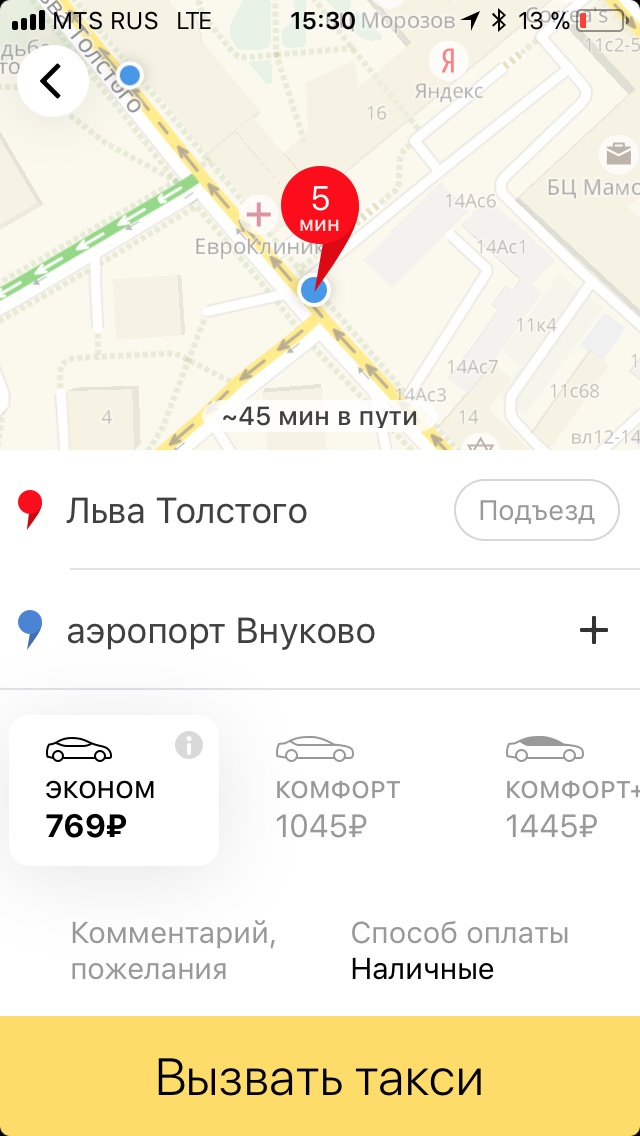
«Было — стало». Слева — старая версия приложения с примерным расчётом стоимости поездки. Справа — текущая версия с точной ценой поездки в разных тарифах.
Очевидно, что показ точной цены поездки в приложении Яндекс.Такси ещё в момент заказа — это само по себе существенное преимущество, которое делает сервис прозрачным для пользователей, поэтому здесь мы мало чем рисковали. Единственное, что оказалось сложно — это объяснить, что если человек приезжает не в ту точку Б, которую он указал при заказе, то вся поездка пересчитывается по таксометру, потому что в таких случаях наши расчёты бессмысленны. Но это уже другая история. Поскольку таких случаев немного, большинство наших пользователей оценило не просто показ финальной цены перед поездкой, но и то, что в конце поездки она не меняется, даже если такси стояло в пробке или водитель её объезжал. И разумеется, они стали чаще указывать точку Б, понимая, что только в этом случае получают такой расчет. Как мы и говорили в начале, если бы наши алгоритмы работали плохо и делали цену хорошей только для пользователя, это могло бы привести к существенной потере заработка водителей и, как следствие, к их оттоку. После того, как цена стала показываться ещё до поездки, количество заказов начало активно расти — многим людям, для которых критична точная стоимость, стало психологически проще пользоваться Яндекс.Такси. Рост заказов привёл к значительному росту утилизации машин такси — то есть к доле за рабочую смену, когда водитель везёт пассажира или едет на заказ, а не тратит время вхолостую. Произошло это ещё и из-за того, что рост улучшил работу других технологий сервиса — например, цепочки заказов. Это алгоритм, который начинает искать следующего клиента ещё до того, как водитель довёз предыдущего — и ищет его в том районе, куда водитель скоро приедет с пассажиром.
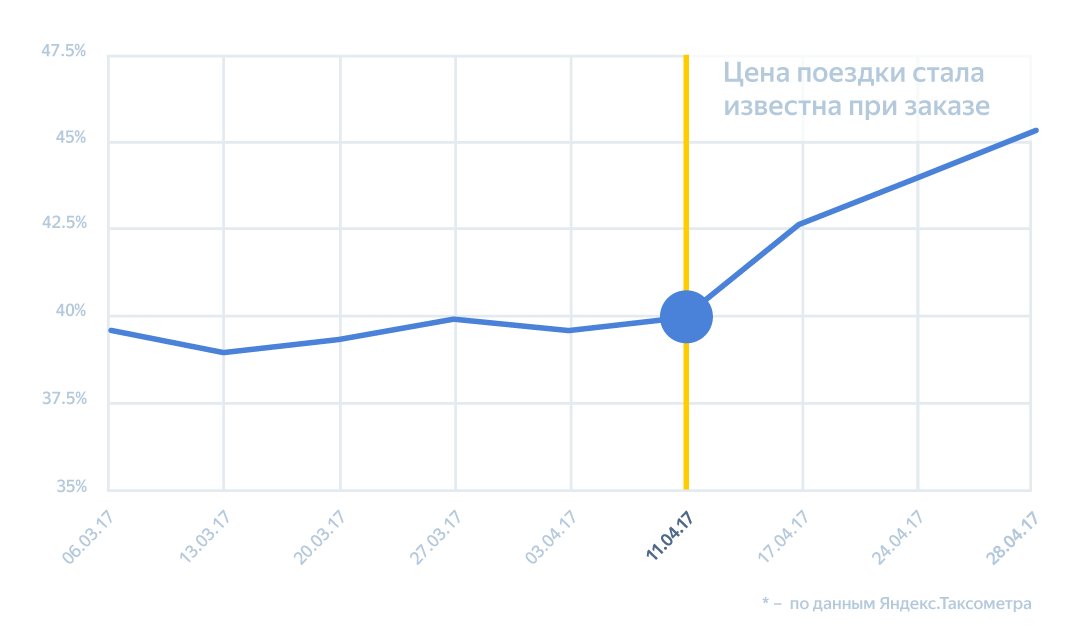
Рост утилизации машин в Москве и области.
Благодаря росту утилизации вырос и самый важный для водителя показатель — earn per hour, средний заработок за час смены: по нашим оценкам, примерно на 15–22% в среднем по России. Хотя некоторые города оказались настоящими рекордсменами, там этот показатель вырос ещё больше. Впереди нас ждёт множество мелких и крупных улучшений модели, вроде подключения CatBoost, про которые мы обязательно расскажем.Источник: habrahabr.ru