Вероятностная интерпретация классических моделей машинного обучения

Этой статьей я начинаю серию, посвященную генеративным моделям в машинном обучении. Мы посмотрим на классические задачи машинного обучения, определим, что такое генеративное моделирование, посмотрим на его отличия от классических задач машинного обучения, взглянем на существующие подходы к решению этой задачи и погрузимся в детали тех из них, что основаны на обучении глубоких нейронных сетей. Но прежде, в качестве введения, мы посмотрим на классические задачи машинного обучения в их вероятностной постановке.

Классические задачи машинного обучения

Две классические задачи машинного обучения — это классификация и регрессия. Давайте посмотрим ближе на каждую из них. Рассмотрим постановку обеих задач и простейшие примеры их решения.

Классификация

Задача классификации — это задача присвоения меток объектам. Например, если объекты — это фотографии, то метками может быть содержание фотографий: содержит ли изображение пешехода или нет, изображен ли мужчина или женщина, какой породы собака изображена на фотографии. Обычно есть набор взаимоисключающих меток и сборник объектов, для которых эти метки известны. Имея такую коллекцию данных необходимо автоматически расставлять метки на произвольных объектах того же типа, что были в изначальной коллекции. Давайте формализуем это определение.
Допустим, есть множество объектов . Это могут быть точки на плоскости, рукописные цифры, фотографии или музыкальные произведения. Допустим также, что есть конечное множество меток . Эти метки могут быть пронумерованы. Мы будем отождествлять метки и их номера. Таким образом в нашей нотации будет обозначаться как . Если , то задача называется задачей бинарной классификации, если меток больше двух, то обычно говорят, что это просто задача классификации. Дополнительно, у нас есть входная выборка . Это те самые размеченные примеры, на которых мы и будем обучаться проставлять метки автоматически. Так как мы не знаем классов всех объектов точно, мы считаем, что класс объекта — это случайная величина, которую мы для простоты тоже будем обозначать . Например, фотография собаки может классифицироваться как собака с вероятностью 0.99 и как кошка с вероятностью 0.01. Таким образом, чтобы классифицировать объект, нам нужно знать условное распределение этой случайной величины на этом объекте .

Задача нахождения при данном множестве меток и данном наборе размеченных примеров называется задачей классификации.

Вероятностная постановка задачи классификации

Чтобы решить эту задачу, удобно переформулировать ее на вероятностном языке. Итак, есть множество объектов и множество меток . — случайная величина, представляющая собой случайный объект из . — случайная величина, представляющая собой случайную метку из . Рассмотрим случайную величину с распределением , которое является совместным распределением объектов и их классов. Тогда, размеченная выборка — это сэмплы из этого распределения . Мы будем предполагать, что все сэмплы независимо и одинаково распределены (i.i.d в англоязычной литературе).

Задача классификации теперь может быть переформулирована как задача нахождения при данном сэмпле .

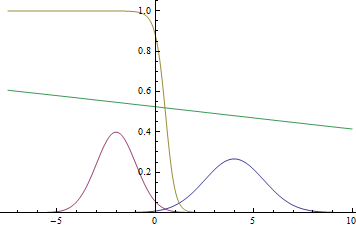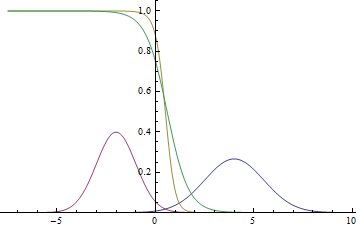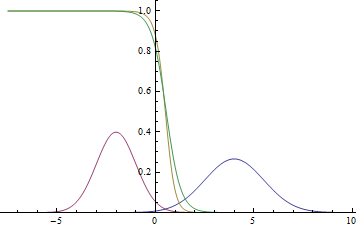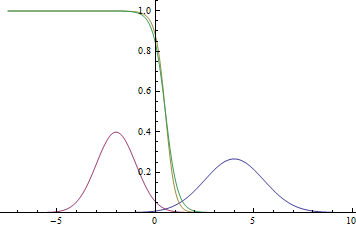
Классификация двух нормальных распределений

Давайте посмотрим, как это работает на простом примере. Положим , , , , . То есть, у нас есть две гауссианы, из которых мы равновероятно сэмплируем данные и нам нужно, имея точку из , предсказать, из какой гауссианы она была получена.

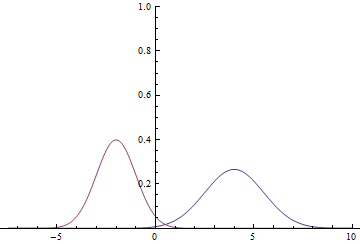
Рис. 1. Плотности распределения и .

Так как область определения гауссианы — вся числовая прямая, очевидно, что эти графики пересекаются, а значит, есть такие точки, в которых плотности вероятности и равны.

Найдем условную вероятность классов:

Т.е.

Вот так будут выглядеть график плотности вероятностей :

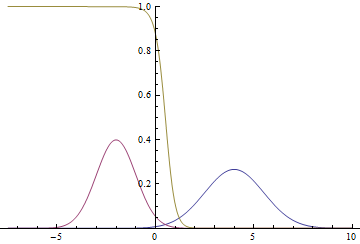
Рис. 2. Плотности распределения , и . там, где две гауссианы пересекаются.

Видно, что близко к модам гауссиан уверенность модели в принадлежности точки конкретному классу очень высока (вероятность близка к нулю или единице), а там, где графики пересекаются модель может только случайно угадывать и выдает .

Метод максимизации правдоподобия

Большая часть практических задач не может быть решена вышеописанным способом, так как обычно не задано явно. Вместо этого обычно имеется набор данных с некоторой неизвестной совместной плотностью распределения . В таком случае для решения задачи используется метод максимального правдоподобия. Формальное определение и обоснование метода можно найти в вашей любимой книге по статистике или по ссылке выше, а в данной статье я опишу его интуитивный смысл.

Принцип максимизации правдоподобия говорит, что если есть некоторое неизвестное распределение , из которого есть набор сэмплов , и некоторое известное параметрическое семейство распределений , то для того, чтобы максимально приблизило , нужно найти такой вектор параметров , который максимизирует совместную вероятность данных (правдоподобие) , которое еще называют правдоподобием данных. Доказано, что при разумных условиях эта оценка является состоятельной и несмещенной оценкой истинного вектора параметров. Если сэмплы выбраны из , то есть данные i.i.d., то совместное распределение распадается на произведение распределений:

Логарифм и умножение на константу — монотонно возрастающие функции и не меняют положений максимумов, потому совместную плотность можно внести под логарифм и умножить на :

Последнее выражение, в свою очередь, является несмещенной и состоятельной оценкой ожидаемого логарифма правдоподобия:

Задачу максимизации можно переписать как задачу минимизации:

Последняя величина называется кросс-энтропией распределений и . Именно ее и принято оптимизировать для решения задач обучения с подкреплением (supervised learning).

Минимизацию на протяжении этого цикла статей мы будем проводить с помощью Stochastic Gradient Descent (SGD), а точнее, его расширения на основе адаптивных моментов, пользуясь тем, что сумма градиентов по подвыборке (так называемому “минибатчу”) является несмещенной оценкой градиента минимизируемой функции.

Классификация двух нормальных распределений логистической регрессией

Давайте попробуем решить ту же задачу, что была описана выше, методом максимального правдоподобия, взяв в качестве параметрического семейства простейшую нейронную сеть. Получившаяся модель называется логистической регрессией. Полный код модели можно найти тут, в статье же освещены только ключевые моменты.

Для начала нужно сгенерировать данные для обучения. Нужно сгенерировать минибатч меток классов и для каждой метки сгенерировать точку из соответствующей гауссианы:

def input_batch(dataset_params, batch_size):     input_mean = tf.constant(dataset_params.input_mean, dtype=tf.float32)     input_stddev = tf.constant(dataset_params.input_stddev,dtype=tf.float32)     count = len(dataset_params.input_mean)     labels = tf.contrib.distributions.Categorical(probs=[1./count] * count)         .sample(sample_shape=[batch_size])     components = []     for i in range(batch_size):         components             .append(tf.contrib.distributions.Normal(                 loc=input_mean[labels[i]],                 scale=input_stddev[labels[i]])             .sample(sample_shape=[1]))     samples = tf.concat(components, 0)     return labels, samples 

Определим наш классификатор. Он будет простейшей нейронной сетью без скрытых слоев:

def discriminator(input):     output_size = 1     param1 = tf.get_variable(         "weights",         initializer=tf.truncated_normal([output_size], stddev=0.1)     )     param2 = tf.get_variable(         "biases",         initializer=tf.constant(0.1, shape=[output_size])     )     return input * param1 + param2 

И запишем функцию потерь — кросс-энтропию между распределениями реальных и предсказанных меток:

labels, samples = input_batch(dataset_params, training_params.batch_size) predicted_labels = discriminator(samples) loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(     labels=tf.cast(labels, tf.float32),     logits=predicted_labels) )

Ниже приведены графики обучения двух моделей: базовой и с L2-регуляризацией:

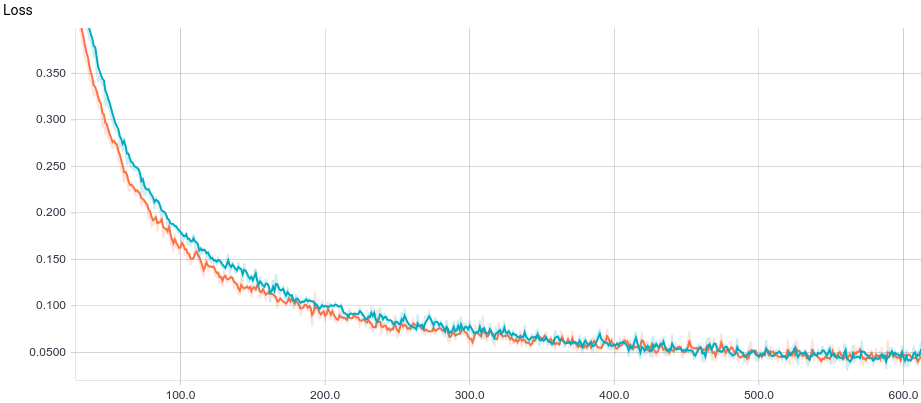
Рис. 3. Кривая обучения логистической регрессии.

Видно, что обе модели быстро сходятся к хорошему результату. Модель без регуляризации показывает себя лучше потому, что в этой задаче не нужна регуляризация, а она слегка замедляет скорость обучения. Давайте взглянем поближе на процесс обучения:

Рис. 4. Процесс обучения логистический регрессии.

Видно, что обучаемая разделяющая поверхность постепенно сходится к аналитически вычисленной, при чем, чем она ближе, тем медленнее сходится из-за все более слабого градиента функции потерь.

Регрессия

Задача регрессии — это задача предсказания одной непрерывной случайной величины на основе значений других случайных величин . Например, предсказание роста человека по его полу (дискретная случайная величина) и возрасту (непрерывная случайная величина). Точно так же, как и в задаче классификации, нам дана размеченная выборка . Предсказать значение случайной величины напрямую невозможно, ведь она случайная и, по сути, является функцией, поэтому формально задача записывается как предсказание ее условного ожидаемого значения:

Регрессия линейно зависимых величин с нормальным шумом

Давайте посмотрим, как решается задача регрессии на простом примере. Пусть есть две независимые случайные величины . Например, это высота дерева и нормальный случайный шум. Тогда мы можем предположить, что возраст дерева является случайной величиной . В таком случае по линейности математического ожидания и независимости и :

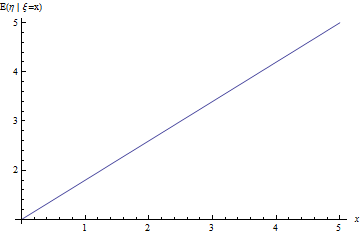
Рис. 5. Линия регрессии задачи про линейно зависимые величины с шумом.

Решение задачи регрессии методом максимального правдоподобия

Давайте сформулируем задачу регрессии через метод максимального правдоподобия. Положим ). Где — новый вектор параметров. Видно, что мы ищем — математическое ожидание , т.е. это корректно поставленная задача регрессии. Тогда

Состоятельной и несмещенной оценкой этого матожидания будет среднее по выборке

Таким образом, для решения задачи регрессии удобно минимизировать среднеквадратичную ошибку на обучающей выборке.

Регрессия величины линейной регрессией

Давайте попробуем решить ту же задачу, что была выше, методом из предыдущего раздела, взяв в качестве параметрического семейства простейшую возможную нейронную сеть. Получившаяся модель называется линейной регрессией. Полный код модели можно найти тут, в статье же освещены только ключевые моменты.

Для начала нужно сгенерировать данные для обучения. Сначала мы генерируем минибатч входных переменных , после чего получаем сэмпл исходной переменной :

def input_batch(dataset_params, batch_size):     samples = tf.random_uniform([batch_size], 0., 10.)     noise = tf.random_normal([batch_size], mean=0., stddev=1.)     labels = (dataset_params.input_param1 * samples + dataset_params.input_param2 + noise)     return labels, samples 

Определим нашу модель. Она будет простейшей нейронной сетью без скрытых слоев:

def predicted_labels(input):     output_size = 1     param1 = tf.get_variable(         "weights",         initializer=tf.truncated_normal([output_size], stddev=0.1)     )     param2 = tf.get_variable(         "biases",         initializer=tf.constant(0.1, shape=[output_size])     )     return input * param1 + param2 

И запишем функцию потерь — L2-расстояние между распределениями реальных и предсказанных значений:

labels, samples = input_batch(dataset_params, training_params.batch_size) predicted_labels = discriminator(samples) loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(     labels=tf.cast(labels, tf.float32),     logits=predicted_labels) ) 

Ниже приведены графики обучения двух моделей: базовой и с L2-регуляризацией:

Рис. 6. Кривая обучения линейной регрессии.

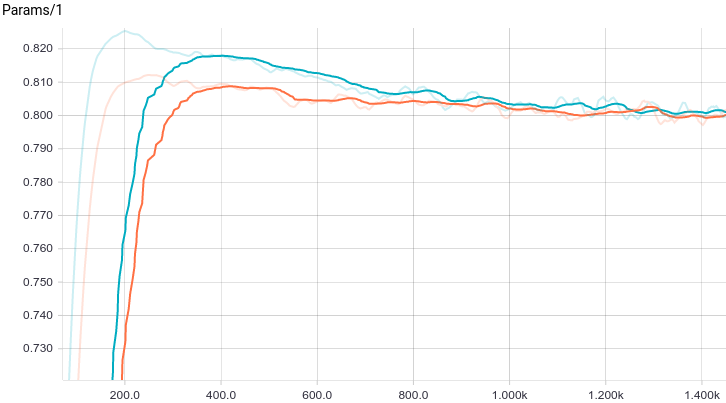
Рис. 7. График изменения первого параметра с шагом обучения.

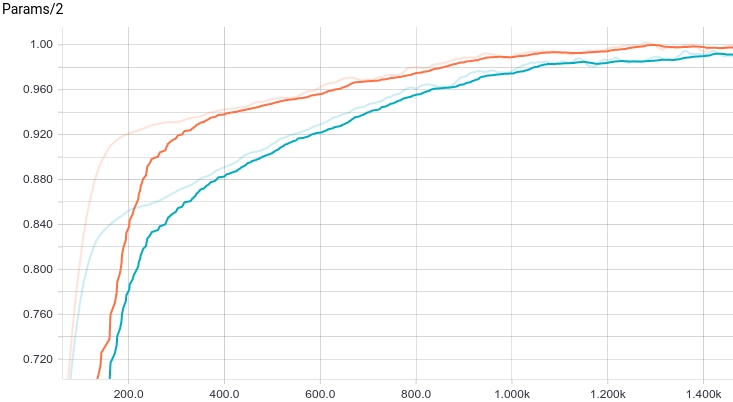
Рис. 8. График изменения второго параметра с шагом обучения.

Видно, что обе модели быстро сходятся к хорошему результату. Модель без регуляризации показывает себя лучше потому, что в этой задаче не нужна регуляризация, а она слегка замедляет скорость обучения. Давайте взглянем поближе на процесс обучения:

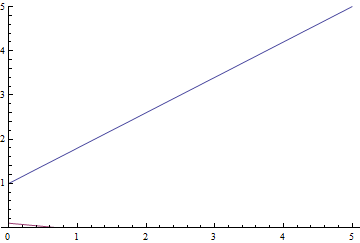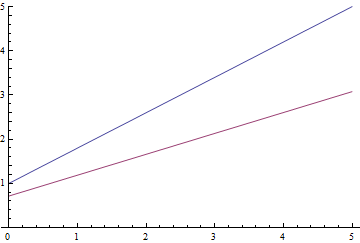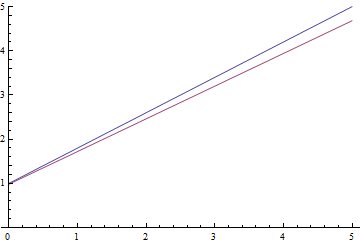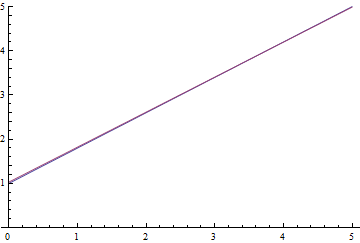
Рис. 9. Процесс обучения линейной регрессии.

Видно, что обучаемое математическое ожидание постепенно сходится к аналитически вычисленному, при чем, чем оно ближе, тем медленнее сходится из-за все более слабого градиента функции потерь.

Другие задачи

В дополнение к изученным выше задачам классификации и регрессии есть и другие задачи так называемого обучения с учителем, в основном сводящиеся к отображению между точками и последовательностями: Object-to-Sequence, Sequence-to-Sequence, Sequence-to-Object. Так же есть и большой спектр классических задач обучения без учителя: кластеризация, заполнение пробелов в данных, и, наконец, явная или неявная аппроксимация распределений, которая и используется для генеративного моделирования. Именно о последнем классе задач будет идти речь в этом цикле статей.

Генеративные модели

В следующей главе мы посмотрим, что такое генеративные модели и чем они принципиально отличаются от рассмотренных в этой главе дискриминативных. Мы посмотрим на простейшие примеры генеративных моделей и попробуем обучить модель, генерирующую сэмплы из простого распределения данных.

Благодарности

Спасибо Olga Talanova за ревью этой статьи. Спасибо Sofya Vorotnikova за комментарии, редактирование и проверку английской версии. Спасибо Andrei Tarashkevich за помощь в верстке.