Полёты на падающих снежинках

1. Вступление

В очень сильно нагруженных порталах или API может возникать потребность в применении алгоритмов машинного обучения, например, с целью классификации пользователей. В рамках данной заметки будет показан процесс реализации некоторых высокопроизводительных линейных моделей, а также даны объяснения основных теоретических принципов.

2. Парная линейная зависимость

Начну свой рассказ с наиболее часто используемых и простых моделей. Предположим, что существует пара метрик с явно выраженной линейной зависимостью. Визуально отобразим данные: значение первой метрики — это положение точки по абсциссе, а значение второй метрики — положение точки по ординате. На рисунке видно, что при увеличении объясняющей переменной (её ещё называют предиктором, регрессором или независимой переменной) происходит увеличение и зависимой переменной. Для наглядности теоретические примеры будут показаны на R:

a <- c(1, 5, 5, 6, 4, 8, 9, 11, 15, 18, 22, 28, 29, 31, 31, 32) b <- c(1, 5, 6, 4, 5, 8, 9, 10, 17, 19, 22, 28, 28, 30, 30, 32)  plot(a, b) abline(lm(b ~ a), col = "blue")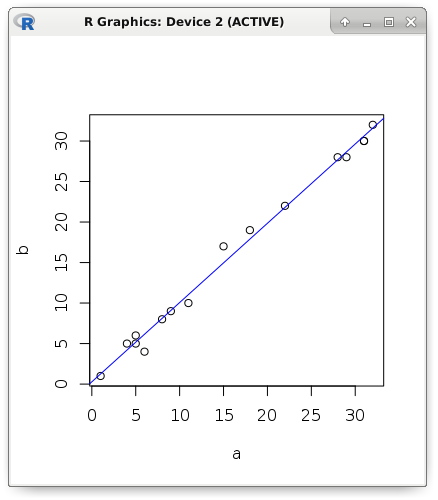

Пусть необходимо написать такой алгоритм, который должен выявить факт наличия линейной зависимости, а также измерить степень её выраженности. Формально говоря, необходимо вычислить линейный коэффициент корреляции Карла Пирсона. Предлагаю вспомнить теоретические основы и более детально разобраться с формулами расчёта:

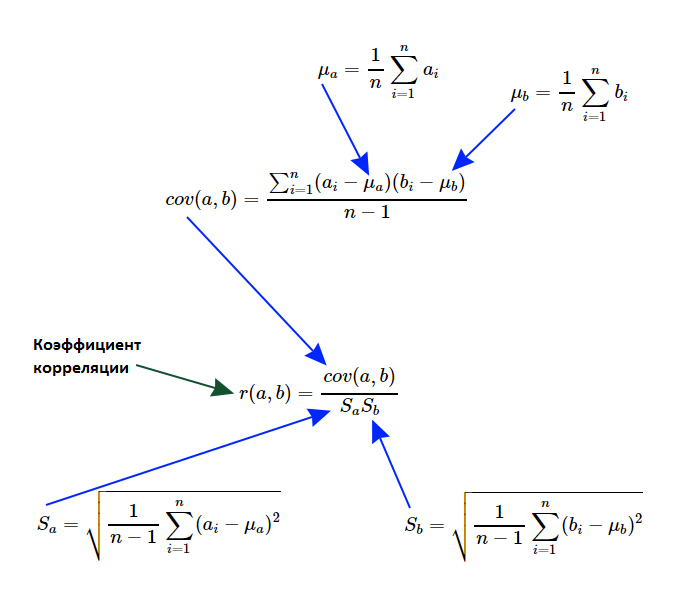
Прежде всего, нас заинтересует такая характеристика множеств, которую называют дисперсией случайной величины. Если от каждого элемента множества отнять среднее значение, а результат возвести в квадрат, то получим новое множество, среднее значение которого называют дисперсией случайной величины для генеральной совокупности. Как вы понимаете, если все элементы исходного множества были одинаковые, то дисперсия равна нулю, а чем элементы сильнее отклоняются от среднего значения, тем больше будет дисперсия. А ещё она не может быть отрицательным числом.

var_a <- sum((a - mean(a)) ^ 2) / (length(a) - 1)  c(var(a), var_a)  # 127.2625 127.2625  c(sd(a), sqrt(var_a))  # 11.28107 11.28107

Обратите внимание, что в показанном выше примере мы делили не на мощность множества, а на единицу меньше его. Другими словами, мы рассчитывали дисперсию для выборки, а не для генеральной совокупности. А так как разница среднего и элемента возводилась в квадрат, то теперь есть смысл извлечь квадратный корень из дисперсии, тем самым получив среднеквадратическое отклонение. Для поиска взаимосвязи нужно знать и среднеквадратическое отклонение второго множества:

var_b <- sum((b - mean(b)) ^ 2) / (length(b) - 1)  c(var_b, var(b)) # 122.7833 122.7833  c(sd(b), sqrt(var_b)) # 11.08076 11.08076

Теперь необходимо вычислить такую меру линейной зависимости двух величин, как ковариация. Формула очень похожа на дисперсию, более того, если множества будут идентичными, то мы действительно получим дисперсию случайной величины. Порядок аргументов может быть произвольным (допустимо множества менять местами), так как по формуле видна симметричность — ковариация A и B равна ковариации B и A.

cov_ab <- sum((a - mean(a)) * (b - mean(b))) / (length(a) - 1)  c(cov(a, b), cov_ab) # 124.525 124.525

Собственно, линейный коэффициент корреляции Карла Пирсона — это просто отношение ковариации и произведения среднеквадратических отклонений множеств. В отличии от ковариации его весьма удобно интерпретировать: он всегда находится в интервале от -1 до 1. Чем ближе он к единице, тем выше линейная корреляция. А близость к -1 показывает отрицательную корреляцию (проще говоря, чем больше одна переменная, тем меньше другая). Если он не сильно отклоняется от нуля, то это свидетельствует о слабой зависимости. Очень важно подчеркнуть, что речь идёт только о линейной зависимости без остро выраженных выбросов, иначе применение этого коэффициента не будет иметь смысла.

cov_ab / (sqrt(var_a) * sqrt(var_b)) # 0.9961772  cor(a, b) # 0.9961772

Линейный коэффициент корреляции можно вычислять после нормализации или стандартизации данных, так как зависимость будет сохранена. Рассмотрим обе упомянутых модификации исходных данных — стандартизацию и нормализацию. В первом случае от каждого элемента множества вычитали среднее значение (получили силу отклонения этой величины от среднего), а потом разделили его на среднеквадратическое отклонение. В итоге получили новое множество, в котором среднее значение равно 0, а дисперсия 1. Во втором случае мы вычитали из каждого элемента минимальное значение и делили на вариационный размах (данные будут в интервале от 0 до 1).

# Нормализация nm <- function(a) {     (a - mean(a)) / sd(a) }  # Стандартизация snt <- function(a) {     (a - min(a)) / (max(a) - min(a)) }  cor(a, b) # 0.9961772  cor(nm(a), nm(b)) # 0.9961772  cor(snt(a), snt(b)) # 0.9961772

Наблюдая парную линейную зависимость аппроксимируем её прямой. Это позволит предсказать значение одной метрики, если известна только вторая. Так как мы исследуем именно парную линейную зависимость, то следует вычислить только два параметра: константа (пересечение, смещение, intercept) и коэффициент единственного предиктора, т.е. наклон прямой (slope). Для расчёта коэффициента предиктора достаточно умножить корреляцию на результат деления среднеквадратических отклонений предиктора и зависимой переменной. Пересечение можно найти ещё проще: вычесть из среднего значения предиктора результат произведения коэффициента и среднего значения зависимой переменной.

slope <- cor(a, b) * (sd(b) / sd(a)) intercept <- mean(b) - (slope * mean(a))  c(intercept, slope) # 0.2803261 0.9784893

Если зависимость будет не функциональная, а стохастическая, то появится некоторая ошибка. Рассмотрим пример. Попробуем с помощью линейной регрессии предсказать значение зависимой переменной, если известен только предиктор. Красным цветом я отображаю предсказанные значения, которые находятся строго на прямой, а чёрным — фактическое значение:

y <- (0.2803261 + (0.9784893 * a))  plot(a, b) points(a, y, col = "red") abline(lm(b ~ a), col = "blue")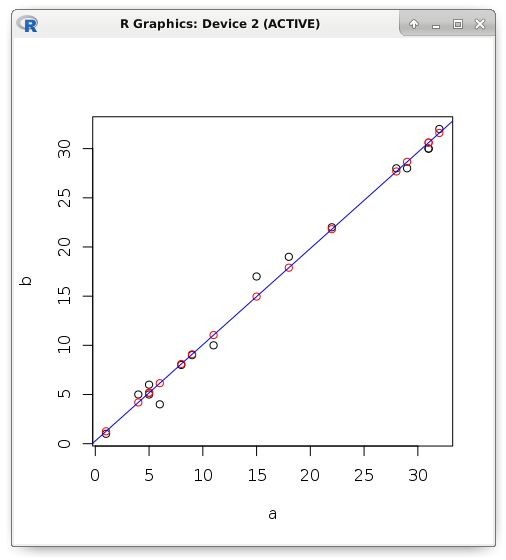

Ошибкой называют разницу между фактическим и предсказанным значением. Например, в языке программирования R описательная статистика ошибки выводится в пункте «Residuals». Показаны робастные (устойчивые к помехам) результаты измерения. Середина отсортированного множества (медиана) устойчива к выбросам (помехам), равно как и нижний или верхний квартиль. Среднее значение тут не используется, так как оно не устойчиво к выбросам. Не сложно догадаться, что максимум и минимум — это своеобразные рекорды (самая сильная ошибка).

summary(lm(b ~ a)) # Residuals: #      Min       1Q   Median       3Q      Max # -2.15126 -0.61350 -0.09749  0.50744  2.04233 #  # Coefficients: #             Estimate Std. Error t value Pr(>|t|) # (Intercept)  0.28033    0.44308   0.633    0.537 # a            0.97849    0.02293  42.669 3.17e-16 *** # --- # Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 # 

Кроме этого, показаны intercept и коэффициент предиктора, которые мы вычислили ранее. Соседний столбец — это стандартная ошибка. Рядом показана t-статистика, которая проверяет нулевую гипотезу о том, что коэффициент равен нулю (так как ноль вычитать из коэффициента нет смысла, то просто разделим коэффициент на стандартную ошибку). Уровень значимости достаточно большой, что позволяет отклонить нулевую гипотезу. Для наглядности рассчитаем вручную полученные показатели:

e <- (b - y)  # Residuals: c(min(e), quantile(e, .25), median(e), quantile(e, .75), max(e)) # -2.15126190 -0.61349440 -0.09748515  0.50744140  2.04233440  # Std. Error (a) sqrt(sum(e ^ 2) / ((length(e) - 2) * sum((a - mean(a)) ^ 2))) # 0.02293208  # t value (a) 0.9784893 / 0.02293208 # 42.66902  # Pr(>|t|) (a) round((pt(42.66902, df = 14, lower.tail = FALSE) * 2), digits = 18) # 3.17e-16

Теперь оценим точность модели посредством следующих метрик: MSE, MAE и RMSE. Название MSE происходит от английского Mean Square Error. Это средний квадрат ошибки. А метрика MAE (Mean Absolute Error) — это среднее абсолютное значение ошибки. Другими словами, в первом случае мы получаем среднее значение квадрата ошибки, а во втором — среднее модуля ошибки. Метрика RMSE (Root Mean Square Error) является просто квадратным корнем из MSE.

mae <- mean(abs(e)) mse <- mean(e ^ 2) rmse <- sqrt(mse)  c(mae, mse, rmse) # 0.7131298 0.8783887 0.9372239  hist(e, breaks = 10, col = "blue")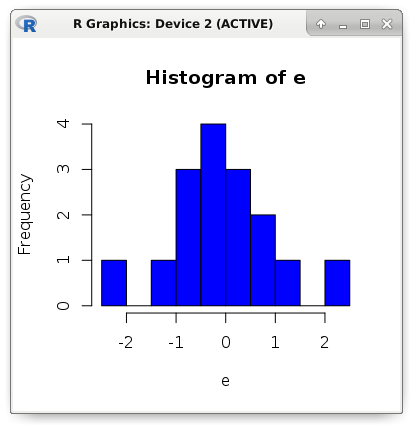

3. Перенос существующих моделей

Перейдём к более практическому аспекту. Допустим, что существует очень высоконагруженный API, в который необходимо добавить функционал выявления значения зависимой переменной по значению единственного предиктора. Фактически, речь идёт о задаче аппроксимации (регрессии). Реализация линейной функции будет отличаться очень компактным и высокопроизводительным кодом.

Будем считать, что API написан на PHP7. Напомню, что внешняя система ничего не должна знать о принципах работы модели. Вся логика работы будет инкапсулирована в одном классе. Известны только требования к входным данным и к возвращаемому значению. Как и предполагает шаблон проектирования strategy, клиент будет использовать любой класс, имплементирующий интерфейс. Этот интерфейс потребует реализацию одного метода, принимающего единственный аргумент (предиктор), а возвращающего другое скалярное значение — зависимую переменную.

<?php declare(strict_types = 1);  interface IModel {     /**      * @param float $x      * @return float      */      public function predict(float $x): float; }  class Example implements IModel {     /**      * @var float      */     const SLOPE = 0.9784893;      /**      * @var float      */     const INTERCEPT = 0.2803261;      /**      * @param float $x      * @return float      */      public function predict(float $x): float     {         return (self::INTERCEPT + (self::SLOPE * $x));     } }  class Client {     /**      * @var IModel      */     private $_model;      /**      * @param IModel $model      */      public function setModel(IModel $model)     {         $this->_model = $model;     }      /**      * @param float $x      * @return float      */      public function run(float $x): float     {         return $this->_model->predict($x);     } }  $client = new Client(); $client->setModel(new Example());  echo $client->run(17);

Для сравнения можно написать полный код для парной линейной зависимости:

<?php declare(strict_types = 1);  class Model {     /**      * @var float      */     public $slope = 0.0;      /**      * @var float      */     public $intercept = 0.0;      /**      * @param array $x      * @param array $y      */      public function fit(array $x, array $y)     {         $this->slope = Stat::cor($x, $y) * (Stat::sd($y) / Stat::sd($x));         $this->intercept = Stat::mean($y) - ($this->slope * Stat::mean($x));     }      /**      * @param float $x      * @return float      */      public function predict(float $x): float     {         return ($this->intercept + ($this->slope * $x));     } }

Методы описательной статистики я реализовал в отдельном классе:

<?php declare(strict_types = 1);  class Stat {     /**      * @param array $values      * @return float      */      public static function max(array $values): float     {         return max($values);     }      /**      * @param array $values      * @return float      */      public static function min(array $values): float     {         return min($values);     }      /**      * @param array $values      * @return float      */      public static function sum(array $values): float     {         return array_sum($values);     }      /**      * @param array $values      * @return float      */      public static function mean(array $values): float     {         return self::sum($values) / count($values);     }      /**      * @param array $values      * @return float      */      public static function variance(array $values): float     {         $mean = self::mean($values);         $pow = array_map(function($v) use ($mean) {             return pow($v - $mean, 2);         }, $values);          return self::sum($pow) / (count($pow) - 1);     }      /**      * @param array $values      * @return float      */      public static function sd(array $values): float     {         return sqrt(self::variance($values));     }      /**      * @param array $a      * @param array $b      * @return float      */      public static function cov(array $a, array $b): float     {         $meanA = self::mean($a);         $meanB = self::mean($b);          $diff = [];         for($i = 0; $i < count($a); $i++) {             $diff[] = ($a[$i] - $meanA) * ($b[$i] - $meanB);         }          return self::sum($diff) / (count($diff) - 1);     }      /**      * @param array $a      * @param array $b      * @return float      */      public static function cor(array $a, array $b): float     {         return self::cov($a, $b) / (self::sd($a) * self::sd($b));     } }

Усложним задачу. Пусть количество предикторов будет произвольным. Это уже не прямая, а гиперплоскость в многомерном пространстве. И сменим тип задачи с аппроксимации на классификацию. Например, с помощью логистической регрессии была решена задача бинарной классификации. Мы хотим использовать эту статистическую модель в своём невероятно сильно нагруженном сервисе, скажем, для классификации пользователей. Для решения задачи нам не нужен сам алгоритм обучения модели, а только параметры разделяющей гиперплоскости.

В этой ситуации принцип работы модели останется прежним. Точно также следует суммировать результаты умножения предикторов на соответствующие им коэффициенты. После чего к полученной сумме добавляется intercept. Иногда вместо смещения добавляют искусственный константный предиктор, тогда вся формула будет сводиться только к сумме произведений предикторов с их коэффициентами (скалярное произведение вектора весов на вектор признаков).

Для задачи классификации мы просто сравним результат расчёта с заранее заданным порогом. Если значение больше, то ему присваивают первый класс, иначе — нулевой. Перенос такой модели будет идентичным. В этом и заключаются два важнейших преимущества подобных линейных моделей — компактный код и очень высокая производительность. Это позволяет буквально на лету выявлять класс наблюдения по вектору признаков.

# Загрузка данных dataset <- read.csv('dataset.csv')  # Для наглядности визуально отобразим данные pairs(dataset, col = factor(dataset$class))  # Тренировка модели логистической регрессии model <- glm(formula = class ~ ., data = dataset, family = binomial)  # Получение необходимых коэффициентов b <- model$coefficients  # Вероятности нам не нужны, просто разделеним точки nc <- (b[1] + (dataset$alpha * b[2]) + (dataset$beta * b[3])) > 0 plot(dataset$alpha, dataset$beta, col = factor(nc))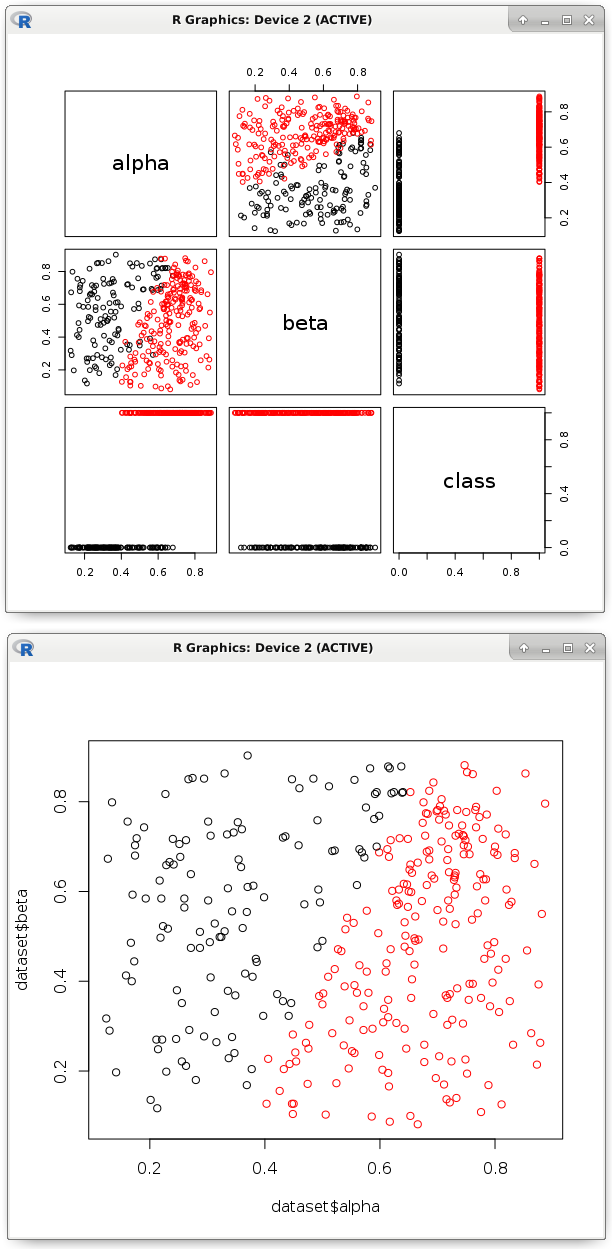

На изображении видно, что подобная линейная функция разделила точки на два класса. Собственно, её параметры и нужно экспортировать в код на другом языке программирования. Как мы убедились, это несложная задача. Данный процесс весьма хорошо поддаётся автоматизации. Главное быть уверенным, что такая гиперплоскость будет правильно классифицировать, а все предикторы действительно необходимы.

Обучать модель и проверять её точность следует на разных наборах данных. Существуют ряд метрик точности классификации, основные из которых мы обязательно рассмотрим. Прежде всего, предлагаю вспомнить метрику вероятности точного ответа. Она рассчитывается как количество верных ответов, делённых на количество всех ответов.

test <- factor(as.logical(dataset$class))  length(nc) # 345  table(test == nc) # FALSE  TRUE #    17   328  328 / 345 # 0.9507246

А что, если доля наблюдений одного из классов будет всего одна тысячная процента? Тут даже выдающий константу классификатор покажет замечательный результат. Есть смысл отобразить confusion matrix. В бинарной классификации могут быть только четыре исхода предсказания метки класса. Истинным положительным результатом называют правильное угадывание положительного класса (TRUE предсказан как TRUE). Истинным отрицательным — верное угадывание отрицательного класса (FALSE предсказан как FALSE). Логично предположить, что ложный положительный — это FALSE предсказанный как TRUE, а ложный отрицательный — это TRUE предсказанный как FALSE. Посмотрим на конкретном примере:

table(nc, test) #          test #   nc   FALSE TRUE #  FALSE   120    8 #  TRUE      9  208

Где «nc» — это ответ классификатора, а «test» — истинный ответ. Определим долю положительных ответов классификатора, которые действительно были положительными (точность, precision). А также полноту (recall), т.е. какую долю настоящих положительных удалось выявить этой моделью. Смысл у этих показателей следующий: точность показывает степень доверия классификатору, если он дал положительный ответ. Другими словами, насколько мы можем быть уверены, что это действительно положительный класс. А вот полнота показывает охват выявляющей способности, т.е. долю выявленных положительных. Если мы боимся ошибочно назвать класс положительным, то важнее точность. Когда нужно найти как можно больше положительных, то важнее полнота.

library(caret)  precision <- posPredValue(factor(nc), test, positive = T) # 0.9585253  recall <- sensitivity(factor(nc), test, positive = T) # 0.962963  # Метрика F1 является средним гармоническим полноты и точности f1 <- (2 * precision * recall) / (precision + recall) # 0.960739

Рассчитаем вручную точность и полноту. Достаточно подставить значения из confusion matrix:

# precision (ИстП / ИстП + ЛожП) 208 / (208 + 9) # 0.9585253  # recall (ИстП / ИстП + ЛожОтр) 208 / (208 + 8) # 0.962963

4. Оценка важности предикторов

Допустим, производилось комплексное психологическое исследование людей. Одна половина испытуемых страдает неврозом, а у другой всё хорошо. В чём отличия? Или иной пример: измерили показатели оборудования — одни устройства работают хорошо, а с другими проблема. Что влияет на это? Интуитивно можно предположить, что следует попробовать поискать корреляцию между зависимой переменной и каждым из предикторов. Вдруг окажется, что, скажем, метрика качества топлива сильно коррелирует с долговечностью (чем лучше топливо, тем долговечнее работа устройства). Или посмотреть различия средних значений предикторов у наблюдений разных классов.

Однако, попробуем визуально отобразить наш набор данных. Видна некоторая условная граница, после которой точки меняют цвет. Она проходит в районе 0.5 по предиктору «alpha». Это видно и по гистограмме его распределения (разными цветами показано). А по предиктору «beta» таких явных различий не наблюдается.

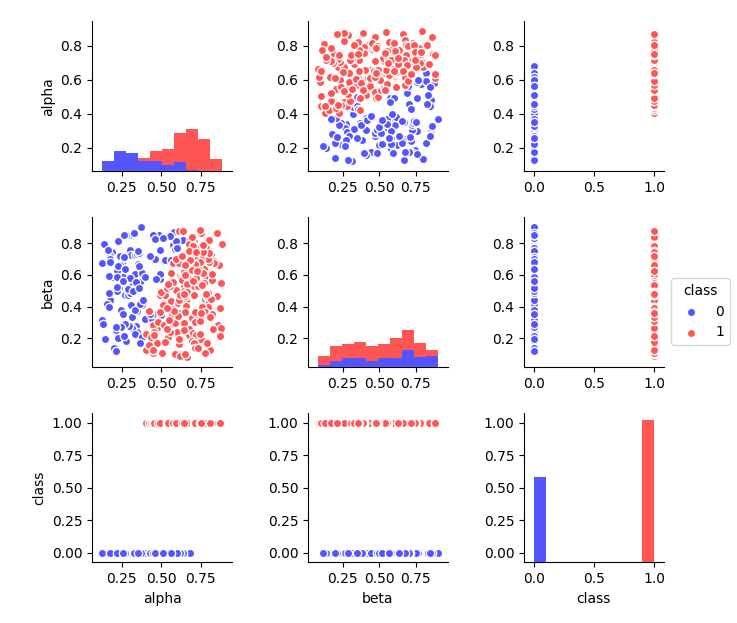
Интуитивно понятно, что несмотря на ошибку (некоторые точки окажутся неправильно классифицированными) такой критерий будет эффективнее решать проблему, чем любое возможное разделение по предиктору «beta». Следовательно, важность «alpha» будет достаточно высокой. После разделения вероятность встретить точку нужного класса значительно возрастает. Чтобы выявить разницу вначале вычислим вероятность без разделения.

table(dataset$class) #   0   1  # 129 216  length(dataset$class) # 345  c(129 / 345, 216 / 345) # 0.373913 0.626087

Зная вероятности вычислим метрику однородности данных (если только представители одного класса, то показатель Gini impurity будет равен 0). Gini impurity вычисляется как сумма квадратов вероятностей, которую отняли от единицы.

# Gini impurity gini <- function(p) {     (1 - sum(p ^ 2))  }  gini(c(0.373913, 0.626087)) # 0.4682041

Разделим все точки по упомянутому ранее условию. Суть сводится к интуитивно понятной логике: мы хотим выбрать наиболее эффективное разделение по наиболее информативному предиктору.

node_1 <- subset(dataset, alpha > .5)  table(node_1$class) #   0   1  #  25 197  length(node_1$class) # 222  # Разнообразие снижено gini(c(25/222, 197/222)) # 0.199862

Повторим процедуру рекурсивно с каждым новым полученным подмножеством. Так будет происходить до некоторого условия остановки, например, пока не останутся только наблюдения одного класса. Это хорошо описывается деревом решений, где в узлах соответствующие условия проверки (сравнение предиктора с константой), а в терминальных узлах (листьях) наблюдения одного класса. Так как дерево будет стараться в первую очередь брать наиболее эффективные предикторы, то условия разделения по ним будет скапливаться в близких к корню узлах. Получается, что уровень (глубина) разделения по предиктору отражает его важность.

node_2 <- subset(node_1, beta < .29)  table(node_2$class) #   1 #  34  length(node_2$class) # 34  # Это уже будет терминальный узел gini(c(0/34, 34/34)) # 0

Согласитесь, что делать это вручную не самая комфортная задача. Вот тут на помощь приходят алгоритмы машинного обучения. К сожалению, ансамбли деревьев решений не умеют объяснять (вернее, сложно интерпретировать огромное количество деревьев решений) различие между классами, но они могут рассчитывать важность предикторов. Это также относится к задачам аппроксимации, где принцип работы похожий, только критерий разделения будет отличаться.

На этом наборе данных было максимально очевидно, что один из предикторов обладает очень высокой значимостью. Посмотрим, как он коррелирует с меткой класса:

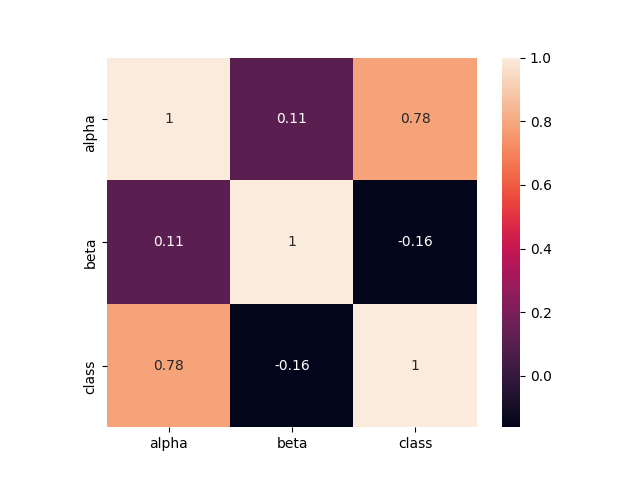
Видны различия и в среднем значении разных классов. Предлагаю посмотреть описательную статистику (примеры на Python и R):

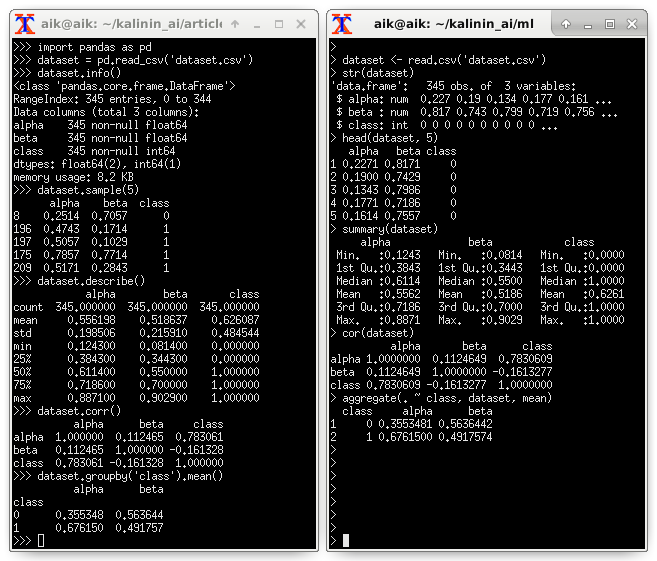
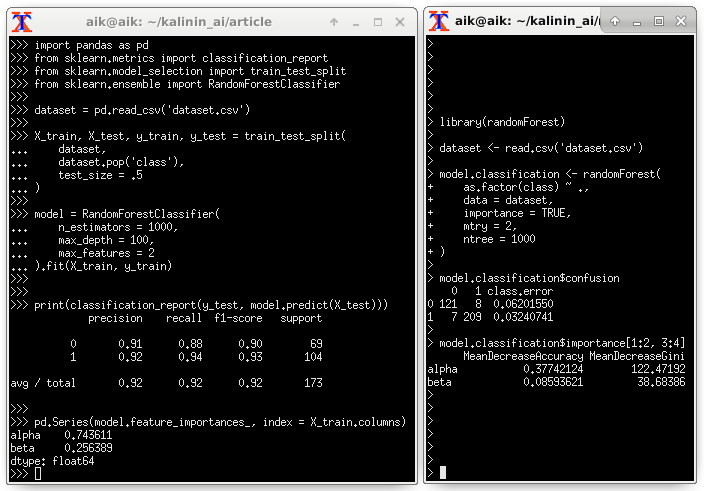
Оценка важности предикторов посредством Random Forest:

5. Выводы

У описанных в заметке линейных моделей есть два основных преимущества, которые позволяют довольно легко переносить их в различные проекты. Во-первых, это компактность кода (только несколько математических операций). Во-вторых, очень высокая производительность. Однако, у всего есть недостатки. К сожалению, если точки плохо поддаются разделению гиперплоскостью или зависимость слабо ей аппроксимируется, то эффективность окажется на неприемлемо низком уровне.

6. Приложение

Использованные фрагменты исходного кода (Python) для выявления степени важности предикторов:

import pandas as pd  dataset = pd.read_csv('dataset.csv') dataset.info() dataset.sample(5) dataset.describe() dataset.corr() dataset.groupby('class').mean()

import seaborn as sns import matplotlib.pyplot as plt  dataset.hist(bins = 20, figsize = (6, 6)) plt.show()  sns.heatmap(dataset.corr(), square = True, annot = True) plt.show()  sns.pairplot(     data = dataset,     hue = 'class',     size = 2,     palette = 'seismic' ) plt.show()

import pandas as pd from sklearn.metrics import classification_report from sklearn.model_selection import train_test_split from sklearn.ensemble import RandomForestClassifier  dataset = pd.read_csv('dataset.csv')  X_train, X_test, y_train, y_test = train_test_split(     dataset,     dataset.pop('class'),     test_size = .5 )  model = RandomForestClassifier(     n_estimators = 1000,     max_depth = 100,      max_features = 2 ).fit(X_train, y_train)  print(classification_report(y_test, model.predict(X_test)))  pd.Series(model.feature_importances_, index = X_train.columns)

from catboost import CatBoostClassifier from sklearn.model_selection import KFold from sklearn.metrics import confusion_matrix, f1_score  kf = KFold(n_splits = 3, shuffle = True) dataset = pd.read_csv('dataset.csv')  y = dataset.pop('class').values X = dataset.values columns = dataset.columns  for train_index, test_index in kf.split(X):     X_train, X_test = X[train_index], X[test_index]     y_train, y_test = y[train_index], y[test_index]      model = CatBoostClassifier(         calc_feature_importance = True     ).fit(X_train, y_train)      y_pred = model.predict(X_test)      print(confusion_matrix(y_test, y_pred))     print(f1_score(y_test, y_pred))     print(list(zip(columns, model.feature_importances_)))