Обнаружение аномалий в данных сетевого мониторинга методами статистики

МЕНЮ

Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту

ТЕМЫ

Новости ИИРазработка ИИВнедрение ИИРабота разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика

Авторизация

RSS

RSS новости
Когда наблюдаемых метрик становится слишком много, отслеживание всех графиков самостоятельно становится невозможным. Обычно в этом случае для менее значимых метрик используют проверки на достижение критичных значений. Но даже если значения подобраны хорошо, часть проблем остается незамеченной. Какие это проблемы и как их обнаруживать — под катом.


Disclaimer
Автор хотя и имеет математическое образование, никак не связан ни с Data Mining, ни со статистическим анализом. Данный материал является результатом исследования, проведенного с целью выяснить возможность написания модуля поиска аномалий (пусть даже слабого) для разрабатываемой системы мониторинга.

Что ищем в двух картинках

Примеры аномалий на графиках

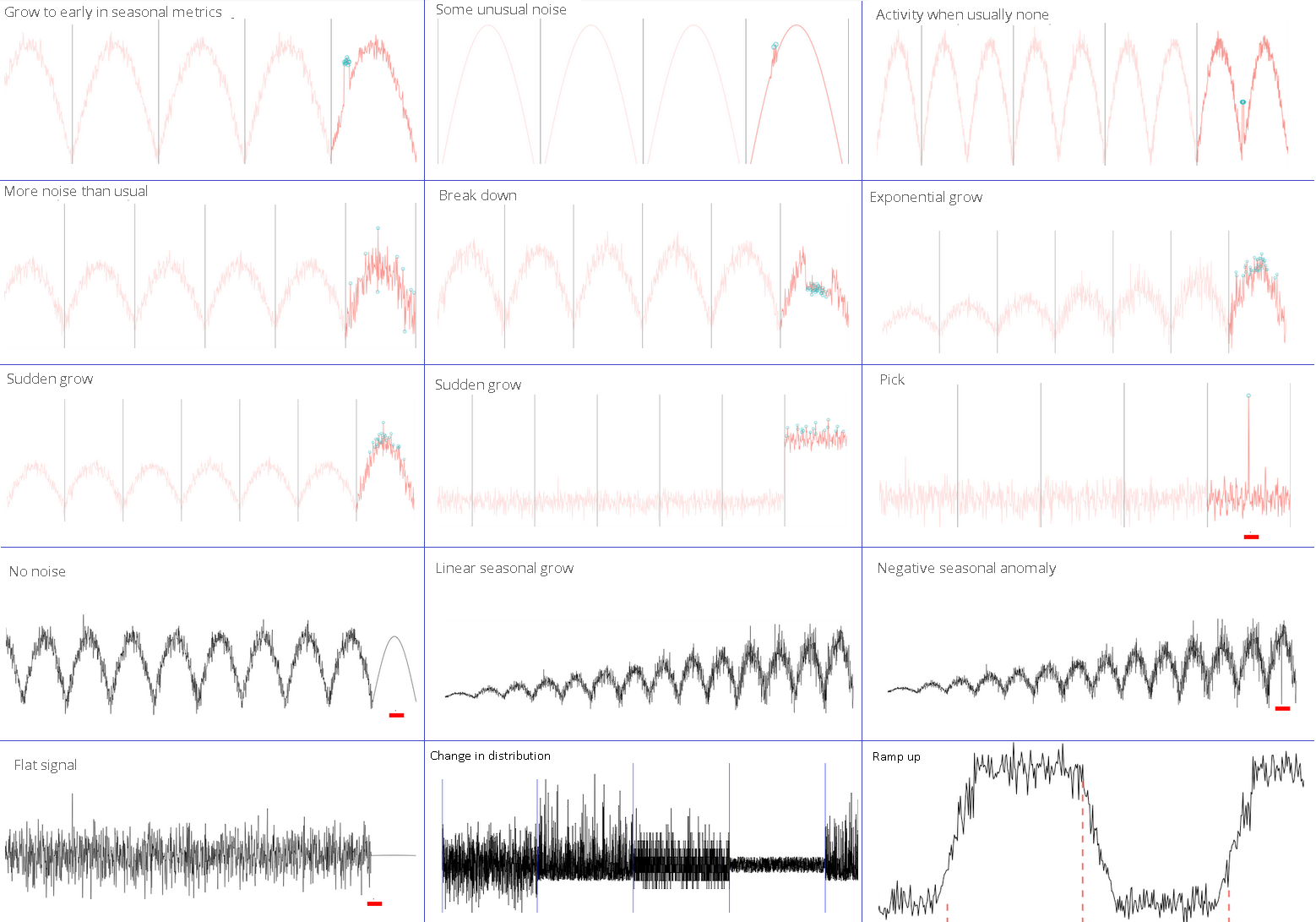
Источник Anomaly.io

Конечно в реальности, не всегда все так просто: только на б), д) и е) явная аномалия.

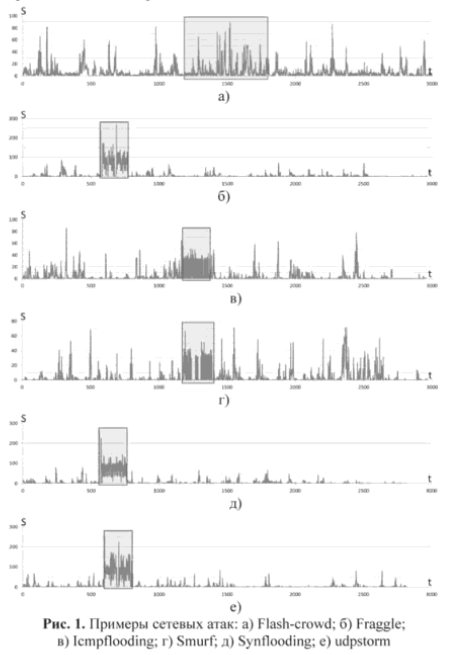
Источник cyberleninka.ru

Текущее положение дел

Коммерческие продукты почти всегда представлены в виде сервиса, использующего как статистику, так и машинное обучение. Вот некоторые из них: AIMS, Anomaly.io (прекрасный блог с примерами), CoScale (возможность интеграции, напр. с Zabbix), DataDog, Grok, Metricly.com и Azure (от Microsoft). У Elastic есть модуль X-Pack на основе машинного обучения.

Open-source продукты, которые можно развернуть у себя:

  • Atlas от Netflix — in-memory база данных для анализа временных рядов. Поиск выполняется методом Хольта-Винтерса.
  • Banshee от Eleme. Для обнаружения используется всего один алгоритм, основанный на правиле трех сигм.
  • Стек KALE от Etsy, состоящий из двух продуктов Skyline, для обнаружения проблем в реальном времени, и Oculus для поиска взаимосвязей. Похоже заброшен.
  • Morgoth — фреймворк для обнаружения аномалий в Kapacitor (модуль уведомлений InfluxDB). Из коробки имеет: правило трех сигм, тест Колмогорова-Смирнова и отклонение Дженсена-Шеннона.
  • Prometheus — набирающая популярность система мониторинга, в которой можно самостоятельно реализовывать некоторые алгоритмы поиска, используя стандартный функционал.
  • RRDTool — база данных, используемая, например, в Cacti и Munin. Умеет делать прогноз методом Хольт-Винтерса. О том, как это можно использовать — в статье Мониторинг прогнозированием, оповещения о потенциальном сбое
  • ~2000 репозитариев на GitHub

На мой взгляд open-source по качеству поиска значительно уступает. Чтобы понять, как работает поиск аномалий и можно ли исправить ситуацию, придется немного окунуться в статистику. Математические детали упрощены и скрыты под спойлерами.

Модель и её компоненты

Для анализа временного ряда используют модель, которая отражает предполагаемые особенности (компоненты) ряда. Обычно модель состоит из трех компонент:
  • Тренд — отражает общее поведение ряда в плане возрастания или убывания значений.
  • Сезонность — периодичные колебания значений, связанные, например, с днем недели или месяца.
  • Случайное значение — то, что останется от ряда после исключения других компонент. Здесь и будем искать аномалии.

Можно включить дополнительные компоненты, например циклическую, как множитель тренда,
аномальную (Catastrophic event) или социальную (праздники). Если тренд или сезонность в данных не просматриваются, то соответсвующие компоненты из модели можно исключить.

В зависимости от того, как связаны между собой компоненты модели, определяют её тип. Так, если все компоненты складываются, чтобы получить наблюдаемый ряд, то говорят, что модель аддиктивна, если умножаются, то мультипликативна, если что-то умножается, а что-то сладывается, то смешаная. Обычно тип модели выбирается исследователем на основе предварительного анализа данных.

Декомпозиция

Выбрав тип модели и набор компонент можно приступать к декомпозиции временного ряда, т.е. его разложению на компоненты.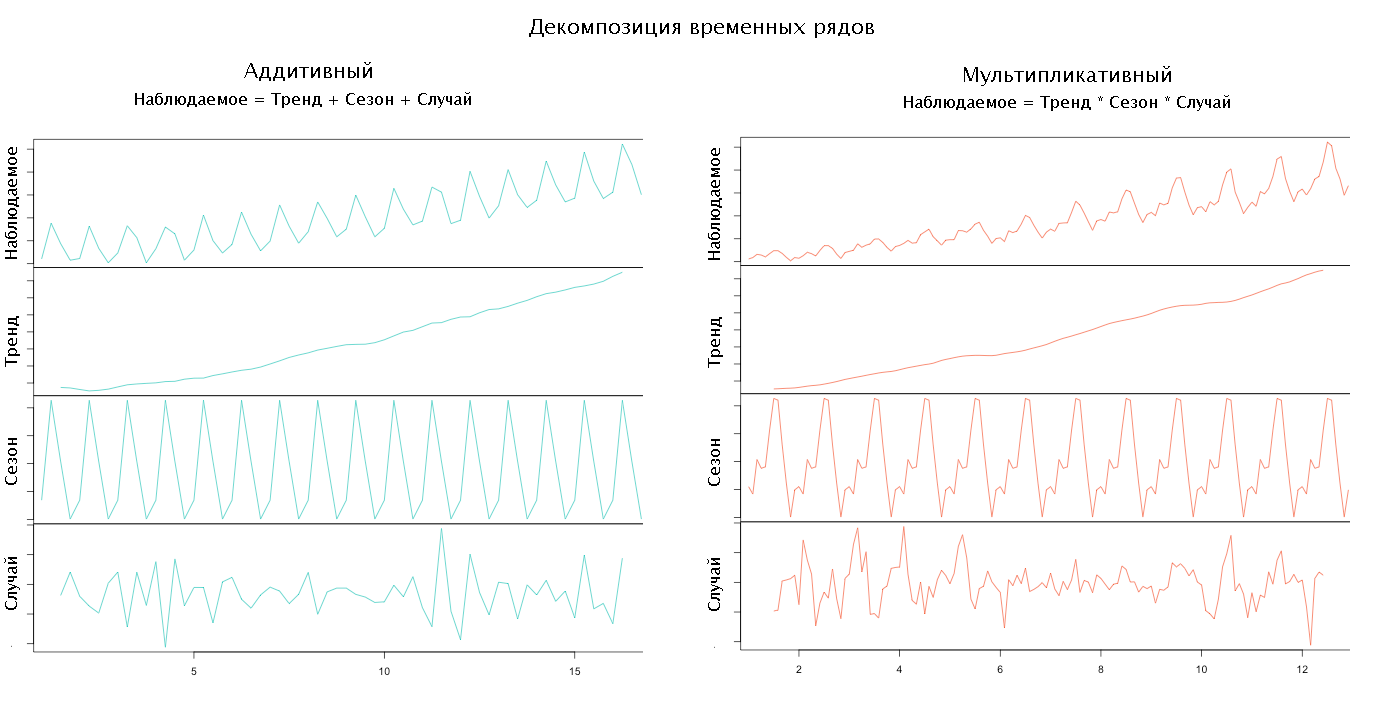
Источник Anomaly.io

Сперва выделяем тренд, сгладив исходные данные. Метод и степень сглаживания выбираются исследователем.

Методы сглаживания рядов: скользящая средняя, экспоненциальное сглаживание и регрессия
Самый простой способ сгладить временной ряд — использовать вместо исходных значений половину суммы соседних

$s_n = frac {x_n + x_{n-1}}{2}$

Если использовать не одно, а несколько предшедствующих значений, т.е. среднее арифметическое k-соседних значений, то такое сглаживание называется простым скользящим средним с шириной окна k

$s_n = frac {x_n + x_{n-1} + ... + x_{n-k}}{k}$

Если для каждого предыдушего значения использовать какой то свой коэффициент, определяющий степень влияния на текущий, то получим взвешенное скользящее среднeе.

Несколько другой способ — эсконенциальное сглаживание. Сглаженный ряд вычисляется следующим образом: первый элемент совпадает с первым элементом исходного ряда, а вот последующие вычисляются по форумуле

$s_n = alpha x_n + (1 - alpha)s_{n-1}$

Где ? — коэффициент сглаживания, от 0 до 1. Как легко видеть чем ближе ? к 1, тем больше получаемый ряд будет похож на исходный. Для определения линейного тренда можно взять методику расчета линейной регрессии $y_t=a+bx_t+varepsilon_t$ методом наименьших квадратов: $hat{b}=frac {overline{xy}}{overline{x^2}}$, $hat{a}=ar{y}-b ar {x}$, где $ar {x}$ и $ar {y}$ — средние арифметические $x$ и $y$.

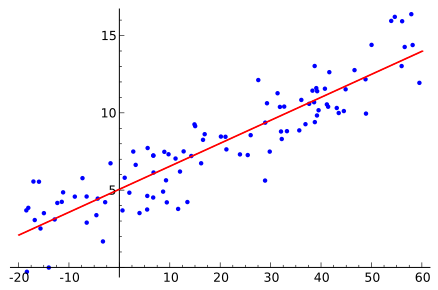
Источник Википедия
Для определения сезонной составляющей из исходного ряда вычитаем тренд или делим на него, в зависимости от типа выбранной модели, и еще раз сглаживаем. Затем делим данные по длине сезона (периоду), обычно это неделя, и находим усредненный сезон. Если длина сезона не известна, то можно попытаться найти её:
Дискретным преобразованием Фурье или авто-корреляцией
Честно признаюсь, что не стал разбираться как работает преобразование Фурье. Кому интересно могут заглянуть в следующие статьи: Detect Seasonality using Fourier Transform in R и Простыми словами о преобразовании Фурье. Насколько я понял, исходный ряд/функция представляется в виде бесконечной суммы элементов и берется несколько первых значимых коэффициентов.

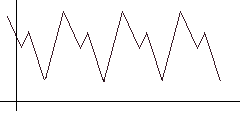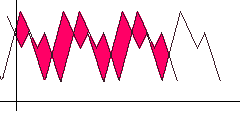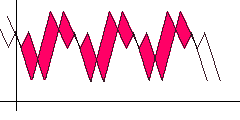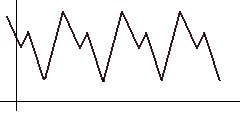Для поиска авто-корреляцией просто сдвигаем функцию вправо и ищем такое положение, чтобы расстояние/площадь между исходной и сдвинутой функцией (выделено красным) было минимально. Очевидно для алгоритма должен быть задан шаг сдвига и максимальный предел, при достижении которого считаем, что поиск периода не удался.
Более подробно о моделях и декомпозиции можно узнать из статей «Extract Seasonal & Trend: using decomposition in R» и «How To Identify Patterns in Time Series Data».

Удалив из исходного ряда тренд и сезонный фактор, получаем случайную компоненту.

Типы аномалий

Если анализировать только случайную компоненту, то многие аномалии можно свести к одному из следующих случаев:
  • Выброс
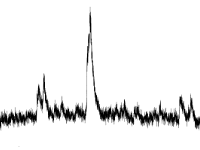
    Выброс в данных временного ряда
    Нахождение выбросов в данных — классическая задача, для решения которой уже имеется хороший набор решений:

    Правило трех сигм, межквартильный размах и другие
    Идея подобных тестов — определить насколько далеко располагается отдельное значение от среднего. Если расстояние отличается от «обычного», то значение объявляется выбросом. Время события при этом игнорируется.

    Считаем, что на входе ряд чисел — $x_1$, $x_2$,… $x_n$, всего $n$ штук. $x_i$ — $i$-ое число.

    Стандартные тесты достаточно просты в реализации и требуют лишь вычисление среднего $ar x = (x_1 + ... + x_n) / n$, стандартного отклонения $S=sqrt{frac{1}{n-1}sum_{i=1}^nleft(x_i-ar{x} ight)^2}$ и иногда медианы $M$ — среднее значение, если упорядочить все числа по возрастанию и взять то, которое по середине.

    Правило трех сигм
    Если $|x_i - ar x| > 3 * S$, то $x_i$ считаем выбросом.

    Z-оценка и уточненный метод Iglewicz и Hoaglin
    $x_i$ — выброс, если $|x_i - ar x|/S$ больше задаваемого порога, обычно равному 3. По сути переписанное правило трех сигм.

    Уточненный метод заключается в следующем: для каждого числа ряда вычисляем $|x_i - M|$ и для получившихся значений находим медиану, обозначаемую $MAD$.
    $x_i$ — выброс, если $0.6745 * |x_i - M|/MAD$ больше порога.

    Межквартильный размах
    Сортируем исходные числа по возрастанию, делим на двое и для каждой части находим медианные значения $Q_1$ и $Q_3$.
    $x_i$ — выброс, если $|x_i - M| > 1.5 * (Q_3 - Q_1)$.

    Тест Граббса
    Находим минимальное $x_{min}$ и максимальное $x_{max}$ значения и для них вычисляем $G_{min} = (ar x - x_{min})/ S$ и $G_{max} = (x_{max} - ar x) / S$. Затем выбираем уровень значимости ? (обычно один из 0.01, 0.05 или 0.1), заглядываем в таблицу критичных значений, выбираем значение для n и ?. Если $G_{min}$ или $G_{max}$ больше табличного значения, то считаем соответствующий элемент ряда выбросом.

    Обычно тесты требуют, чтобы исследовалось нормальное распределение, но зачастую это требование игнорируется.
  • Сдвиг
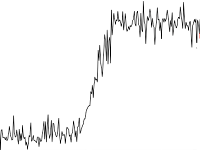
    Сдвиг в данных временного ряда
    Задача обнаружения сдвига в данных неплохо исследована, поскольку встречается в обработке сигналов. Для её решения можно воспользоваться Twitter Breakout Detection. Отмечу, что это оно работает значительно хуже, если анализируется исходный ряд с компонентами сезонности и тренда.
  • Изменение характера (распределения) значений
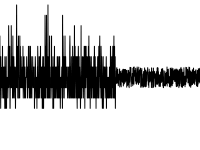
    Изменения распределения в данных временного ряда
    Как и для сдвига, можно использовать тот же пакет BreakoutDetection от Twitter, но с ним не все гладко.
  • Отклонение от «повседневного» (для данных с сезонностью)
    Для обнаружения данной аномалии необходимо сравнить текущий период и несколько предыдущих. Обычно используют

    Метод Хольта-Винтерса

    Метод относится к прогнозированию, поэтому его применение сводится к тому, чтобы сравнить прогнозируемое значение с действительным.

    Основная идея метода в том, что каждая из трех компонент экспоненциально сглаживается, используя отдельный коэффициент сглаживания, поэтому метод зачастую называется тройным экспоненциальным сглаживанием. Формулы рассчета для мультипликативного и аддиктивного сезонов есть в Википедии, а подробности о методе в статье на Хабре.

    Три параметра сглаживания должны выбираться так, чтобы получаемый ряд был «близок» к исходному. На практике такая задача решается перебором, хотя RRDTool требует явного задания этих значений.

    Недостаток метода: требует минимум три сезона данных.

    Другой способ, примененный в Одноклассниках, — выбрать значения из других сезонов, соответсвующие анализируемому моменту, и проверить их совокупность на наличие выброса, например тестом Граббса.

    Также Twitter предлагает AnomalyDetection, который на тестовых данных показывает хорошие результаты. К сожалению, как и BreakoutDetection, он уже два года без обновлений.
  • Поведенческие
    Иногда аномалии могут иметь специфичный характер, который в большинстве случаев должен быть проигнорирован, например, одно значение у двух соседних элементов. В таких случаях требуются отдельные алгоритмы.
  • Совместные аномалии
    Отдельно стоит упомянуть о аномалиях, когда значения двух наблюдаемых метрик поотдельности в пределах нормы, но их совместное появление признак проблемы. В общем случае, нахождение таких аномалий может быть решено кластерным анализом, когда пары значений представляют координаты точек на плоскости и все множество событий делится на две/три группы (кластера) — «норма»/«шум» и «аномалия».


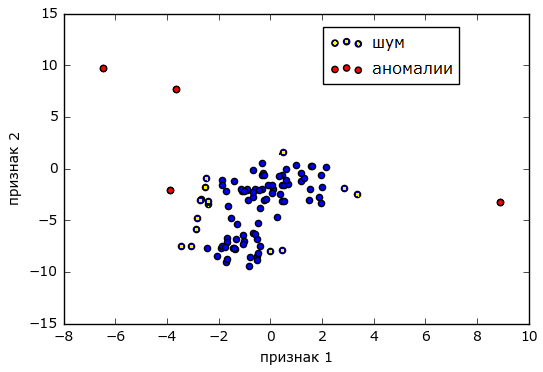
    Источник alexanderdyakonov.wordpress.com

    Более слабый метод состоит в том, чтобы отслеживать насколько метрики зависят друг от друга во времени и в случае, когда зависимость теряется, выдавать сообщение об аномалии. Для этого, вероятно, можно использовать один из методов.

    Линейный коэффициент корреляции Пирсона
    Пусть $x_1, x_2, ..., x_n$ и $y_1, y_2, ..., y_n$ два набора чисел и требуется выяснить имеется ли между ними линейная зависимость. Вычисляем для $x$ среднее $ar x = (x_1 + ... + x_n) / n$ и стандартное отклонение $S_x=sqrt{frac{1}{n-1}sum_{i=1}^nleft(x_i-ar{x} ight)^2}$. Аналогично для $y$.

    Коэффициент корреляции Пирсона

    $r(x, y) = frac {sum_{i=1}^n(x_i - ar x)(y_i - ar y)} {S_x S_y}$

    Чем коэффициент по модулю ближе к 1, тем большая зависимость. Если коэффициент ближе к -1, то зависимость обратная, т.е. рост $x$ связан с убыванием $y$.
    Расстояние Дамерау — Левенштейна

    Пусть есть две строки ABC и ADEC. Чтобы получить из первой вторую, необходимо убрать B и добавить D и E. Если каждой операции удаления/добавления символа и перестановке XY в YX задать стоимость, то суммарная стоимость и будет расстояниеи Дамерау — Левенштейна.

    Для определения похожести графиков можно оттолкнуться от алгоритма, использованного в KALE

    Вначале исходный ряд значений, например, ряд вида [960, 350, 350, 432, 390, 76, 105, 715, 715], нормализуется: ищется максимум — ему будет соответствовать 25, и минимум — ему будет соответствовать 0; таким образом, данные пропорционально распределяются в пределе целых чисел от 0 до 25. В итоге мы получаем ряд вида [25, 8, 8, 10, 9, 0, 1, 18, 18]. Затем нормализованный ряд кодируется с помощью 5 слов: sdec (резко вниз), dec (вниз), s (ровно), inc (вверх), sinc (резко вверх). В итоге получается ряд вида [sdec, flat, inc, dec, sdec, inc, sinc, flat].

    Закодировав два временных ряда таким образом, можно узнать расстояние между ними. И если оно меньше какого то порога, то считать, что графики похожи и связь имеется.

Заключение

Разумеется, многие алгоритмы нахождения аномалий уже реализованы на языке R, предназначенном для статистической обработки данных, в виде пакетов: tsoutliers, strucchange, Twitter Anomaly Detection и других. Подробнее о R в статьях А вы уже применяете R в бизнесе? и Мой опыт введения в R. Казалось бы, подключай пакеты и используй. Однако есть проблема — задание параметров статистических проверок, которые в отличии от критических значений далеко не очевидны для большинства и не имеют универсальных значений. Выходом из данной ситуации может быть их подбор перебором (ресурсоёмко), с редким периодичным уточнением, независимо для каждой метрики. С другой стороны, большая часть аномалий, не связанных с сезонностью, хорошо определяется визуально, что наталкивает на мысль использовать нейронную сеть на отрендеренные графики.

Приложение

Ниже привожу собственные алгоритмы, которые работают сопоставимо с Twitter Breakout по результатам, и несколько быстрее по скорости при реализации на Java Script.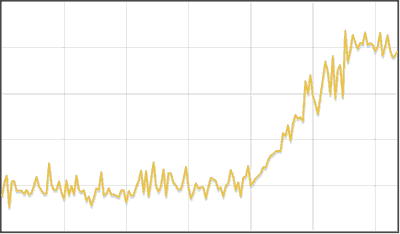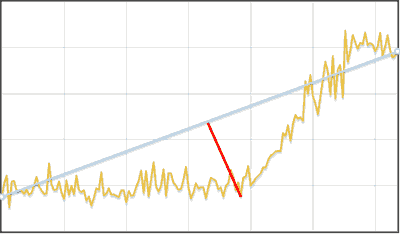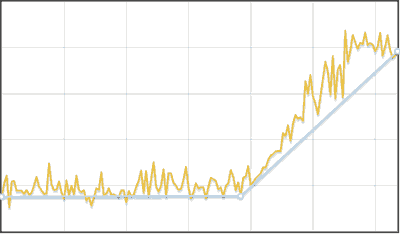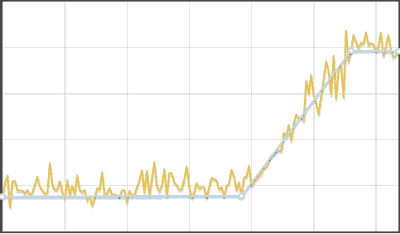
Алгоритм кусочно-линейной аппроксимации временного ряда
Аппроксимация
  1. Если ряд сильно зашумленный, то усредняем, напр. по 5 элементам.
  2. В результат включаем первую и последние точки ряда.
  3. Находим максимально удаленную точку ряда от текущей ломаной и добавляем ее в набор.
  4. Повторяем пока среднее отклонение от ломаной до исходного ряда не будет меньше среднего отклонения в исходном ряде или пока не достигнуто предельное число вершин ломаной (в этом случае, вероятно, апроксимация не удалась).
Алгоритм нахождения сдвига в данных
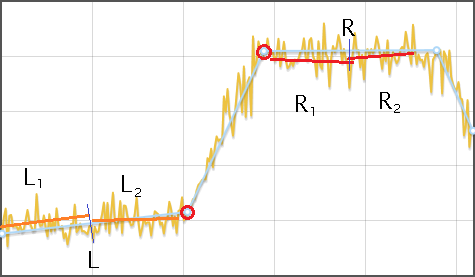
Обнаружение сдвига
  1. Апроксимируем исходный ряд ломаной
  2. Для каждого отрезка ломаной, кроме первого и последнего:
    • Находим его высоту $h$, как разность y-координат начала и конца. Если высота меньше игнорируемого интервала, то такой отрезок игнорируется
    • Оба соседних отрезка $L$ и $R$ делим на двое, каждый участок $L_1$, $L_2$, $R_1$, $R_2$ аппроксимируем своей прямой и находим среднее расстояние от прямой до ряда — $dL_1$, $dL_2$, $dR_1$, $dR_2$.
    • Если $|dL_1 - dL_2|$ и $|dR_1 - dR_2|$ значительно меньше чем $h$, то считаем, что сдвиг обнаружен
Алгоритм нахождения изменений в распределении
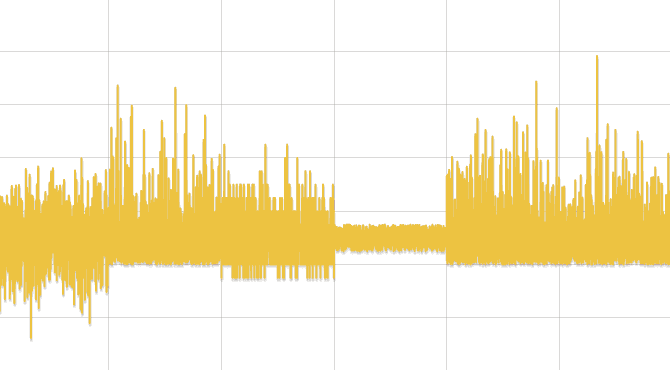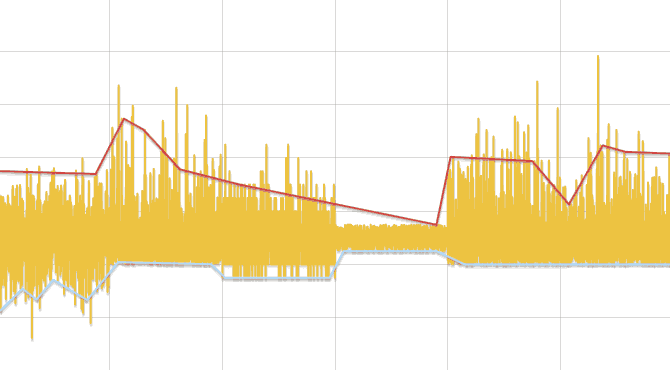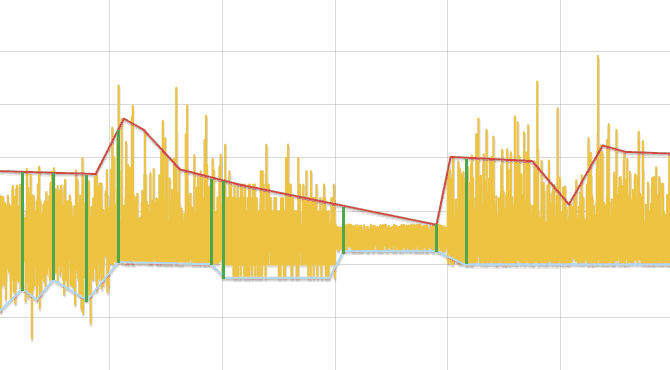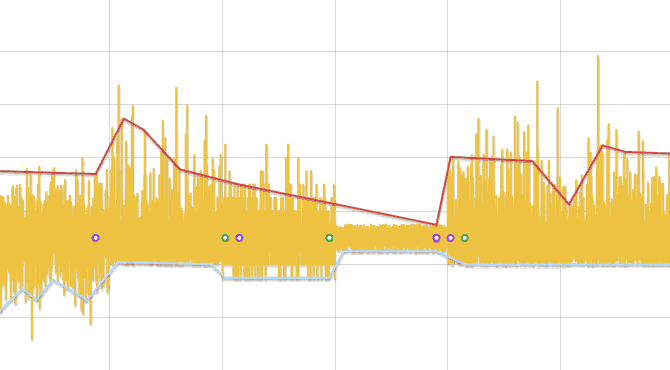
Обнаружение изменения распределения
  1. Исходный ряд разбивается на отрезки, длинной, зависящей от числа данных, но не менее трех.
  2. В каждом отрезке ищется минимум и максимум. Заменяя каждый отрезок его центром, образуется два ряда — минимумы и максимумы. Далее ряды обрабатываются отдельно.
  3. Ряд линейно аппроксимируется и для каждой его вершины, кроме первой и последней, выполняется сравнение данных исходного ряда, лежащих слева и справа до соседних вершин ломаной, тестом Колмогорова-Смирнова. Если разница обнаружена, то точка добавляется в результат.

Тест Колмогорова-Смирнова
Пусть $x_1, x_2, ..., x_{n_1}$ и $y_1, y_2, ..., y_{n_2}$ два набора чисел и требуется оценить существенность различий между ними.

Вначале значения обоих рядов разбиваются на несколько (около десятка) категорий. Далее для каждой категории вычисляется число $f_x$, вошедших в него значений из ряда $x$, и делится на длину ряда $n_1$. Аналогично для ряда $y$. Для каждой категории находим $|f_x - f_y|$ и затем общий максимум $d_{max}$ по всем категориям. Проверяемое значение критерия вычисляется по формуле $lambda = d_{max} frac {n_1 n_2} {n_1 + n_2}$.

Выбирается уровень значимости $alpha$ (один из 0.01, 0.05, 0.1) и по нему определяется критичное значение по таблице. Если $lambda$ больше критичного значения, то считается, что группы различаются существенно.

Источник: habrahabr.ru

Комментарии: