Русскоязычный чат-бот Boltoon: создаем виртуального собеседника

Несколько лет назад было опубликовано интервью, в котором говорят об искусственном интеллекте и, в частности, о чат-ботах. Респондент подчеркивает, что чат-боты не общаются, а имитирует общение.

В них заложено ядро разумных микродиалогов вполне человеческого уровня и построен коммуникативный алгоритм постоянного сведения разговора к этому ядру. Только и всего.

На мой взгляд, в этом что-то есть…

Тем не менее, о чат-ботах много говорят на Хабре. Они могут быть самые разные. Популярностью пользуются боты на базе нейронных сетей прогнозирования, которые генерируют ответ пословно. Это очень интересно, но затратно с точки зрения реализации, особенно для русского языка из-за большого количества словоформ. Мной был выбран другой подход для реализации чат-бота Boltoon.

Boltoon работает по принципу выбора наиболее семантически близкого ответа из предложенной базы данных с последующей обработкой. Этот подход имеет ряд преимуществ:

• Быстрота работы;
• Чат-бот можно использовать для разных задач, для этого нужно загрузить новую базу;
• Боту не требуется дообучение после обновления базы.

Как это работает?

Есть база данных с вопросами и ответами на них.
Необходимо, чтобы бот хорошо распознавал смысл введенных фраз и находил похожие в базе. Например, «как дела?», «как ты?», «как дела у тебя?» значат одно и то же. Т.к. компьютер хорошо работает с числами, а не с буквами, поиск соответствий между введенной фразой и имеющимися нужно свести к сравнению чисел. Требуется перевести всю колонку с вопросами из базы данных в числа, вернее, в векторы из N действительных чисел. Так все документы получат координаты в N-мерном пространстве. Представить его затруднительно, но можно снизить размерность пространства до 2 для наглядности.

В том же пространстве находим координату введенной пользователем фразы, сравниваем ее с имеющимися по косинусной метрике и находим ближайшую. На такой простой идее основан Boltoon.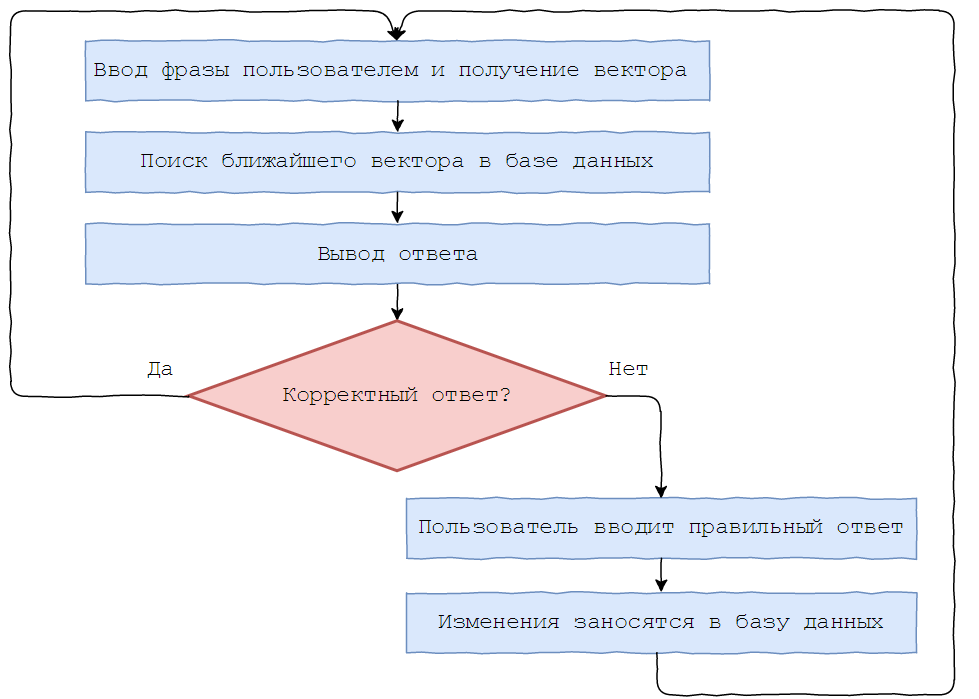

Теперь обо всем по порядку и более формальным языком. Введем понятие «векторное представление текста» (word embeddings) – отображение $$ слова из естественного языка в вектор фиксированной длины (обычно от 100 до 500 измерений, чем выше это значение, тем представление точнее, но сложнее его вычислить).

Например, слова «наука», «книга» могут иметь следующее представление:

v(«наука») = [0.956, -1.987…]
v(«книга») = [0.894, 0.234…]

На Хабре уже писали об этом (подробно можно почитать здесь). Для данной задачи более всего подходит распределенная модель представления текста. Представим, что есть некое «пространство смыслов» — N-мерная сфера, в которой каждое слово, предложение или абзац будут точкой. Вопрос в том, как его построить?

В 2013 году появилась статья «Efficient Estimation of Word Representations in Vector Space», автор Томас Миколов, в которой он говорит о word2vec. Это набор алгоритмов для нахождения распределенного представления слов. Так каждое слово переводится в точку в некотором семантическом пространстве, причем алгебраические операции в этом пространстве соответствуют операциям над смыслом слов (поэтому используют слово семантическое).

На картинке отображено это очень важное свойство пространства на примере вектора «женственности». Если от вектора слова «король» вычесть вектор слова «мужчина» и прибавить вектор слова «женщина», то получим «королеву». Больше примеров Вы можете найти в лекциях Яндекса, также там представлено объяснение работы word2vec «для людей», без особой математики.

На Python это выглядит примерно так (потребуется установить пакет gensim).

import gensim  w2v_fpath = "all.norm-sz100-w10-cb0-it1-min100.w2v" w2v = gensim.models.KeyedVectors.load_word2vec_format(w2v_fpath, binary=True, unicode_errors='ignore') w2v.init_sims(replace=True)  for word, score in w2v.most_similar(positive=[u"король", u"женщина"], negative=[u"мужчина"]):     print(word, score) 

Здесь используется уже построенная модель word2vec проектом Russian Distributional Thesaurus

Получим:

королева 0.856020450592041 бургундская 0.8100876212120056  регентша 0.8040660619735718 клеменция 0.7984248995780945 короля 0.7981560826301575 ангулемская 0.7949156165122986 королевская 0.7862951159477234 анжуйская 0.7808529138565063 лотарингская 0.7741949558258057 маркграфиня 0.7644592523574829 

Подробнее рассмотрим ближайшие к «королю» слова. Существует ресурс для поиска семантически связанных слов, результат выводится в виде эго-сети. Ниже представлены 20 ближайших соседей для слова «король».

Модель, которую предложил Миколов очень проста – предполагается, что слова, находящиеся в схожих контекстах, могут значить одно и то же. Рассмотрим архитектуру нейронной сети.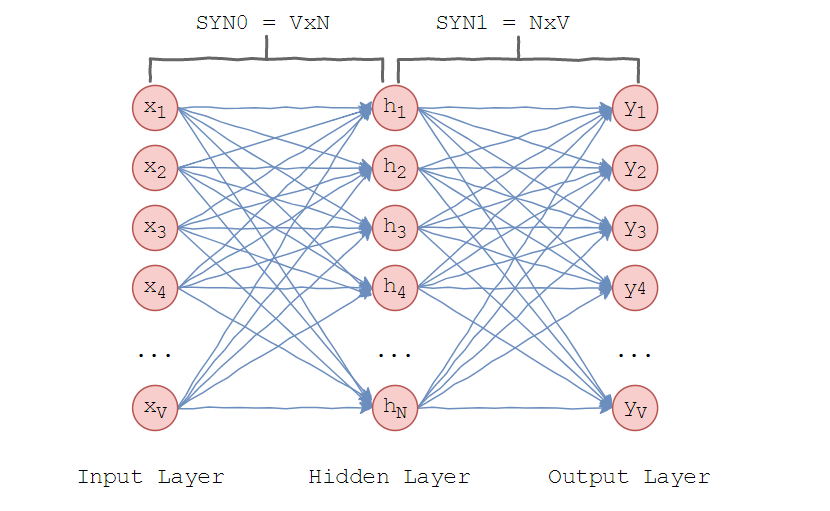

Word2vec использует один скрытый слой. Во входном слое установлено столько нейронов, сколько слов в словаре. Размер скрытого слоя – размерность пространства. Размер выходного слоя такой же, как входного. Таким образом, считая, что словарь для обучения состоит из V слов и N размерность векторов слов, веса между входным и скрытым слоем образуют матрицу SYN0 размера VxN. Она представляет собой следующее.

Каждая из V строк является векторным N-мерным представлением слова.

$$

Аналогично, веса между скрытым и выходным слоем образуют матрицу SYN1 размера NxV. Тогда на входе выходного слоя будет:

$$

где $$ – j-ый столбец матрицы SYN1.

Скалярное произведение – косинус угла между двумя точками в n-мерном пространстве. И эта формула показывает, как близко находятся векторы слов. Если слова противоположные, то это значение -1. Затем используем softmax – «функцию мягкого максимума», чтобы получить распределение слов.

$$

С помощью softmax word2vec максимизирует косинусную меру между векторами слов, которые встречаются рядом и минимизирует, если не встречаются. Это и есть выход нейронной сети. Чтобы лучше понять, как работает алгоритм, рассмотрим корпус для обучения, состоящий из следующих предложений:

«Кот увидел собаку»,
«Кот преследовал собаку»,
«Белый кот взобрался на дерево».
Словарь корпуса содержит восемь слов: [«белый», «взобрался», «дерево», «кот», «на», «преследовал», «собаку», «увидел»]

После сортировки в алфавитном порядке на каждое слово можно ссылаться по его индексу в словаре. В этом примере нейронная сеть будет иметь восемь входных и выходных нейронов. Пусть будет три нейрона в скрытом слое. Это означает, что SYN0 и SYN1 будут соответственно 8x3 и 3x8 матрицами. Перед началом обучения эти матрицы инициализируются небольшими случайными значениями, как это обычно бывает при обучении. Пусть SYN0 и SYN1 инициализированы так:

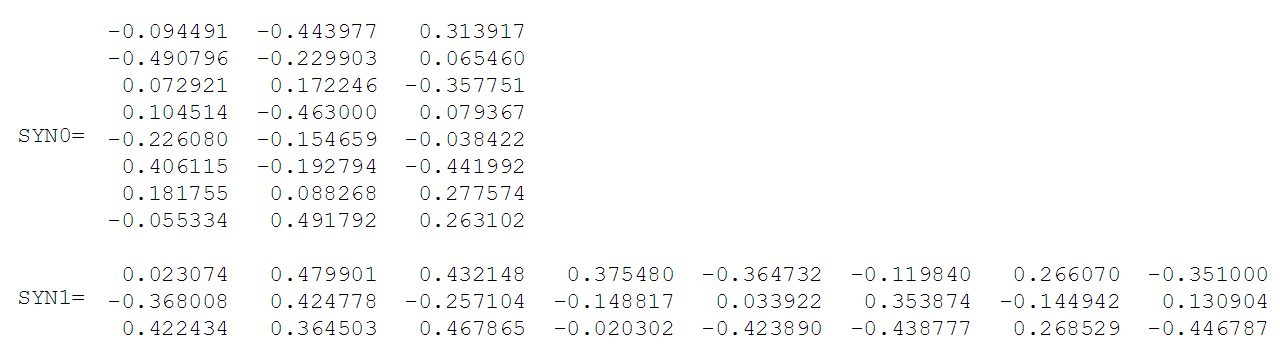Предположим, нейронная сеть должна найти отношение между словами «взобрался» и «кот». То есть, сеть должна показывать высокую вероятность слова «кот», когда «взобрался» подается на вход сети. В терминологии компьютерной лингвистики слово «кот» называется центральное, а слово «взобрался» — контекстное.

В этом случае входной вектор X будет $$ (потому что «взобрался» находится вторым в словаре). Вектор слова «кот» — $$.

При подаче на вход сети вектора, представляющего «взобрался», вывод на нейронах скрытого слоя можно вычислить так:

$$

Обратите внимание, что вектор H скрытого слоя равен второй строке матрицы SYN0. Таким образом, функция активации для скрытого слоя – это копирование вектора входного слова в скрытый слой. Аналогично для выходного слоя:

$$

Нужно получить вероятности слов на выходном слое, $$ для$$, которые отражают отношение центрального слова с контекстным на входе. Для отображения вектора в вероятность, используют softmax. Выход j-го нейрона вычисляется следующим выражением:

$\$\$display\$\$y\_j=P(word\_\{context\}|word\_j\; )=\; frac\{exp^\{val\_jxval\_\{context\}\}\}\{sum\_\{kin\; V\}exp^\{val\_jxval\_k\}\}\; =softmax\$\$display\$\$$

Таким образом вероятности для восьми слов в корпусе равны: [0,143073 0,094925 0,114441 0,111166 0,14492 0,122874 0,119431 0,1448800], вероятность «кота» равна 0,111166 (по индексу в словаре).

Так мы сопоставили каждому слову вектор. Но нам нужно работать не со словами, а со словосочетаниями или с целыми предложениями, т.к. люди общаются именно так. Для это существует Doc2vec (изначально Paragraph Vector) – алгоритм, который получает распределенное представление для частей текстов, основанный на word2vec. Тексты могут быть любой длины: от словосочетания до абзацев. И очень важно, что на выходе получаем вектор фиксированной длины.

На этой технологии основан Boltoon. Сначала мы строим 300-мерное семантическое пространство (как упоминалось выше, выбирают размерность от 100 до 500) на основе русскоязычной Википедии (ссылка на дамп).

Еще немного Python.

model = Doc2Vec(min_count=1, window=10, size=100, sample=1e-4, workers=8)

Создаем экземпляр класса для последующего обучения с параметрами:

• min_count: минимальная частота появления слова, если частота ниже заданной – игнорировать
• window: «окно», в котором рассматривается контекст
• size: размерность вектора (пространства)
• sample: максимальная частота появления слова, если частота выше заданной – игнорировать
• workers: количество потоков

model.build_vocab(documents)

Строим таблицу словарей. Documents – дамп Википедии.

model.train(documents, total_examples=model.corpus_count, epochs=20)

Обучение. total_examples – количество документов на вход. Обучение проходит один раз. Это ресурсоемкий процесс, строим модель из 50 МБ дампа Википедии (мой ноутбук с 8 ГБ RAM больше не потянул). Далее сохраняем обученную модель, получая эти файлы.

Как упоминалось выше, SYN0 и SYN1 – матрицы весов, образованные во время обучения. Эти объекты сохранены в отдельные файлы с помощью pickle. Их размер пропорционален NxVxW, где N – размерность вектора, V – количество слов в словаре, W – вес одного символа. Из этого получился такой большой размер файлов.

Возвращаемся к базе данные с вопросами и ответами. Находим координаты всех фраз в только что построенном пространстве. Получается, что с расширением базы данных не придется переучивать систему, достаточно учитывать добавленные фразы и находить их координаты в том же пространстве. Это и есть основное достоинство Boltoon’а – быстрая адаптация к обновлению данных.

Теперь поговорим об обратной связи с пользователем. Найдем координату вопроса в пространстве и ближайшую к нему фразу, имеющуюся в базе данных. Но здесь возникает проблема поиска ближайшей точки к заданной в N-мерном пространстве. Предлагаю использовать KD-Tree (подробнее о нем можно почитать здесь).

KD-Tree (K-мерное дерево) – структура данных, которая позволяет разбить K-мерное пространство на пространства меньшей размерности посредством отсечения гиперплоскостями.

from scipy.spatial import KDTree  def build_tree(self, ethalon):     return KDTree(list(ethalon.values())) 

Но оно имеет существенный недостаток: при добавлении элемента перестройка дерева осуществляется за O(NlogN) в среднем, что долго. Поэтому Boltoon использует «ленивое» обновление — перестраивает дерево каждые M добавлений фраз в базу данных. Поиск происходит за O(logN).

Для дообучения Boltoon’a был введен следующий функционал: после получения вопроса отправляется ответ с двумя кнопками для оценки качества.

В случае отрицательного ответа, пользователю предлагается скорректировать его, и исправленный результат заносится в базу данных.

Пример диалога с Boltoon’ом с использованием фраз, которых нет в базе данных.

Конечно, это сложно назвать «умом», никаким разумом Boltoon не обладает. Ему далеко до топовых ботов вроде Siri или недавней Алисы, но это не делает его бесполезным и неинтересным, в конце концов, это студенческий проект в рамках летней практики, созданный одним человеком. В дальнейшем, я планирую прикрутить модуль обработки ответов (согласование с полом собеседника, например), запоминание контекста разговора (в рамках нескольких предшествующих сообщений) и обработку опечаток. Надеюсь, получится более разумный Boltoon 2.0. Но это уже разговор для следующей статьи.
P.S. Вы можете потестировать Boltoon'а в telegram по ссылке @boltoon_bot, только не забывайте оценивать каждый полученный ответ, иначе последующие Ваши сообщения будут проигнорированы. И я вижу все логи, кто и что написал, так что давайте соблюдать рамки приличия.
P.P.S. Хочу поблагодарить своих преподавателей PavelMSTU и ov7a за консультации и конструктивную критику по данной статье.