«4 свадьбы и одни похороны» или линейная регрессия для анализа открытых данных правительства Москвы
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Искусственный интеллект
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Разработка ИИГолосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
ИИ теория
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Внедрение ИИКомпьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Big data
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Работа разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2017-10-23 10:25

Несмотря на множество замечательных материалов по Data Science например, от Open Data Science, я продолжаю собирать объедки с пиршества разума и продолжаю делится с вами, своим опытом по освоению навыков машинного обучения и анализа данных с нуля.
В последних статьях мы рассмотрели пару задачек по классификации, в процессе потом и кровью добывая себе данные, теперь пришло время регрессии. Поскольку ничего светотехнического в этот раз под рукой не оказалось, я решил поскрести по другим сусекам.
Помнится, в одной из статей я агитировал читателей посмотреть в сторону отечественных открытых данных. Но поскольку я не барышня из рекламы «кефирчика для пищеварения» или шампуня с лошадиной силой, совесть не позволяла советовать что-либо, не испытав на себе.
С чего начать? Конечно с открытых данных правительства РФ, там же ведь целое министерство есть. Мое знакомство с открытыми данными правительства РФ, было примерно, такое же как на иллюстрации к этой статье. Нет ну не то чтобы мне совсем не был интересен реестр Кинозалов города Новый Уренгой или перечень прокатного оборудования катка в Туле, просто для задачи регрессии они не очень подходят.
Если порыться думаю и на сайте ОД правительства РФ можно найти, что-то путное, просто не очень легко.
Данные Минфина я тоже решил оставить, на потом.
Пожалуй, больше всего мне понравились открытые данные правительства Москвы, там я присмотрел пару потенциальных задачек и выбрал в итоге Сведения о регистрации актов гражданского состояния в Москве по годам
Что вышло из применения минимальных навыков в области линейной регрессии можно в краткой форме посмотреть на GitHub, ну и конечно же заглянув под кат.

Как обычно, в начале статьи расскажу о навыках необходимых для понимания этой статьи.
От вас потребуется:
Если вы совсем новичок в области анализа данных и машинного обучения, посмотрите прошлые статьи цикла в порядке их следования, там каждая статья писалась по «горячим следам» и вы поймете стоит ли Вам тратить время на Data Science.
Все ранее подготовленные статьи ниже под спойлером
Ну и как обещал раньше теперь статьи этого цикла будут комплектоваться содержанием.
Содержание:
Часть I: «Жениться — не лапоть надеть» — Получение и первичный анализ данных.
Часть II: «Один в поле не воин» — Регрессия по 1 признаку
Часть III: «Одна голова хорошо, а много лучше» — Регрессия по нескольким признакам с регуляризацией
Часть IV: «Не все то золото что блестит» — Добавляем признаки
Часть V: «Крой новый кафтан, а к старому примеряй!» — Прогноз тренда
Итак, перейдем подробней к задаче. Наша с Вами цель, откопать какой-нибудь набор данных достаточный для того, чтобы продемонстрировать основные приемы линейной регрессии и самим определить, что мы будем прогнозировать.
В этот раз буду краток и не буду отходить от темы рассмотрев только линейную регрессию (вы же наверняка знаете о существовании и других методов)
Динамика регистрации актов гражданского состояния, нам вполне подойдет.
Это почти сотня записей, разбитых по месяцам, в которых есть данные о количестве свадеб, рождений, установление родительства, смертей, смен имен и т.д.
Для решения задачи регрессии вполне подойдет.
Весь код целиком, размещен на GitHub
Ну а по частям мы его препарируем прямо сейчас.
Для начала импортируем библиотеки:
Затем загрузим данные. Библиотека Pandas позволяет загружать файлы с удаленного сервера, что в общем и целом просто замечательно, при условии, конечно что на портале не изменится алгоритм переадресации страниц.
(надеюсь, что ссылка на скачивание в коде, не накроется, если она перестанет работать пожалуйста напишите в «личку», чтобы я мог обновить)
Посмотрим на данные:
Если мы хотим пользоваться данными о месяцах, их необходимо перевести в понятный модели формат, у scikit-learn есть свои методы, но мы для надежности сделаем руками (ибо не очень много работы) ну и заодно удалим пару бесполезных в нашем случае столбцов с ID и мусором.
Поскольку я не уверен, что табличный вид у всех откроется нормально посмотрим на данные с помощью картинки.
 Построим парные диаграммы, из которых будет понятно, какие столбцы нашей таблицы, линейно зависят друг от друга. Однако сразу все данные мы не будем рассматривать, чтобы потом было, что добавить, поэтому вначале уберем часть данных.
Построим парные диаграммы, из которых будет понятно, какие столбцы нашей таблицы, линейно зависят друг от друга. Однако сразу все данные мы не будем рассматривать, чтобы потом было, что добавить, поэтому вначале уберем часть данных.
Достаточно простой способ выделить(«удалить») часть столбцов из pandas Dataframe, это просто сделать выборку по нужным столбцам:
Ну а теперь можно и график построить.
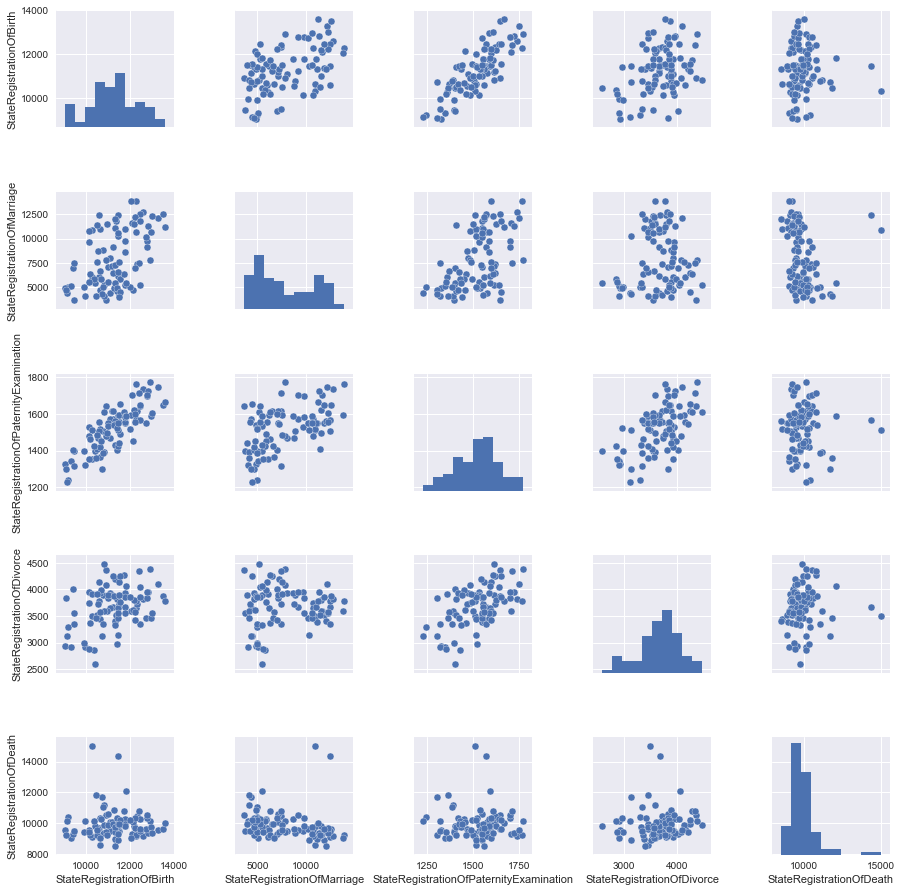
Хорошей практикой является масштабирование признаков, чтобы не сравнивать лошадей с весом копны сена и средним атмосферным давлением в течении месяца.
В нашем случае все данные представлены в одних величинах (количестве зарегистрированных актов), но давайте все же посмотрим, что изменит масштабирование.
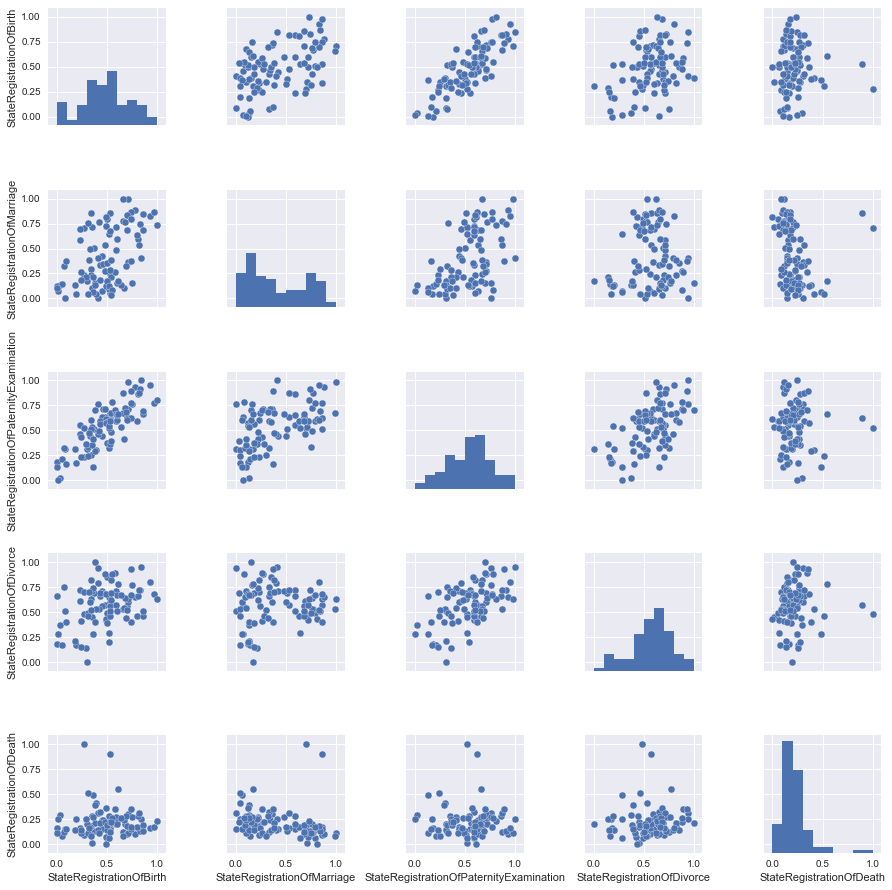
Почти ничего, но для надежности пока будем брать масштабированные данные.
Подготовим данные, а именно выделим два столбца признак и целевую функцию, затем с помощью готовых библиотек поделим данные на обучающую и контрольную выборку (манипуляции в конце кода были нужны, для приведения данных к нужной форме)
Важно отметить, что сейчас несмотря на явную возможность привязаться к хронологии, мы в целях демонстрации рассмотрим данные просто как набор записей без привязки ко времени.
«Скормим» наши данные модели и посмотрим на коэффициент при нашем признаке, а также оценим точность подгонки модели с помощью R^2 (коэффициент детерминации).
Получилось не очень, с другой стороны сильно лучше чем если бы мы «тыкались на угад»
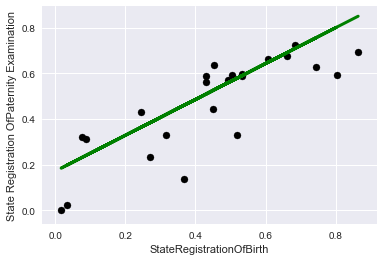
Посмотрим это на графиках, вначале на обучающих данных:

А теперь на контрольных:
Чтобы было интересней давайте выберем другую целевую функцию, которая не так очевидно линейно зависит от признаков.
Чтобы соответствовать названию статью, в качестве целевой функции выберем регистрацию браков.
А все остальные столбцы из набора с картинок парных диаграмм сделаем признаками.
Обучим вначале просто модель линейной регрессии.
Получим результат чуть хуже, чем в прошлом случае (что и не удивительно)
Для борьбы с переобучением и/или отбора признаков, вместе с моделью линейной регрессии обычно используют механизм регуляризации, в данной статьи мы рассмотрим механизм Lasso (L1 – regularization)
Чем больше коэффициент регуляризации альфа, тем активнее модель штрафует большие значения признаков, вплоть до приведения некоторых коэффициентов уравнения регрессии к нулю.
Надо отметить, что тут я делаю прям вот нехорошие вещи, подогнал коэффициент регуляризации под тестовые данные, в реальности так делать не стоит, но нам чисто для демонстрации сойдет.
Посмотрим на вывод:
В данном случае модель с регуляризацией не сильно повышает качество, попробуем добавить еще признаков.
Для начала посмотрим на результаты без регуляризации
С ума сойти! Почти 100% точность!
Как же этот признак можно было назвать бесполезным?!
Ну давайте мыслить здраво, наше количество браков входит в общее количество, поэтому если у нас есть сведения о других признаках, то и точность близится к 100%. На практике это не особо полезно.
Давайте перейдем к нашему «Лассо»
Вначале выберем небольшой коэффициент регуляризации:
Ну ничего сильно не поменялось, это нам не интересно, давайте посмотрим, что будет если его увеличить.
Итак, видим, что почти все признаки были признаны моделью бесполезными, а самым полезным остался признак общего количества записей, так, что если бы нам вдруг пришлось использовать только 1-2 признака мы бы знали, что выбрать, чтобы минимизировать потери.
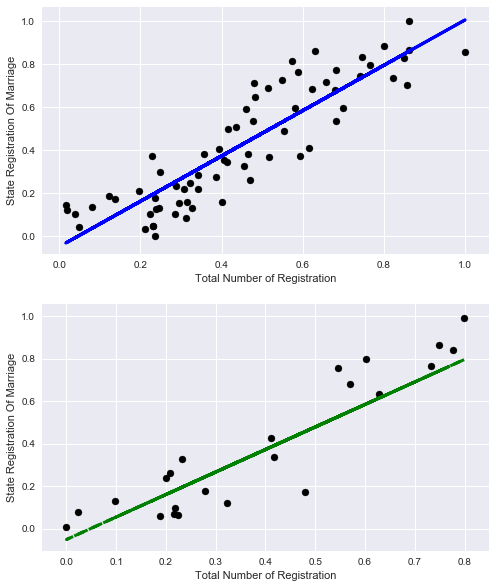
Давайте чисто из любопытства посмотрим как можно было объяснить процент регистрации браков только лишь общим количеством записей.
Ну что же неплохо, но объективно меньше, чем с учётом остальных признаков.
Давайте посмотрим на графики:
Давайте попробуем к исходному набору данных теперь добавить другой бесполезный признак
State Registration Of Name Change (смену имени), можете самостоятельно построить модель и посмотреть, какую долю данных объясняет этот признак (маленькую поверьте на слово).
А мы сразу подберем данные и обучим модель на старых 4х признаках и этом бесполезном
Не будем пробовать регуляризацию она кардинально ничего не изменит, как видно данный признак нам все только портит.
Давайте наконец-то выберем полезный признак.
Все знают, что есть горячий сезон для свадеб (лето и начало осени), а есть тихий сезон (зима).
Меня кстати удивило, что в мае отмечают мало свадеб.
Неплохое повышение качества и главное все соответствует здравой логике.
Для удобства будем считать срок в месяцах с января 2010, для этого напишем простую анонимную функцию, которая нам преобразует данные, в итоге заменим столбец год, на количество месяцев.
Обучаться будем на данных до 2016 года, а будущим для нас станет все что начинается с 2016 года.
Как видно при такой разбивке данных, точность несколько снижается и тем не менее качество предсказания всяко лучше, чем пальцем в небо.
Убедимся посмотрев на графики.
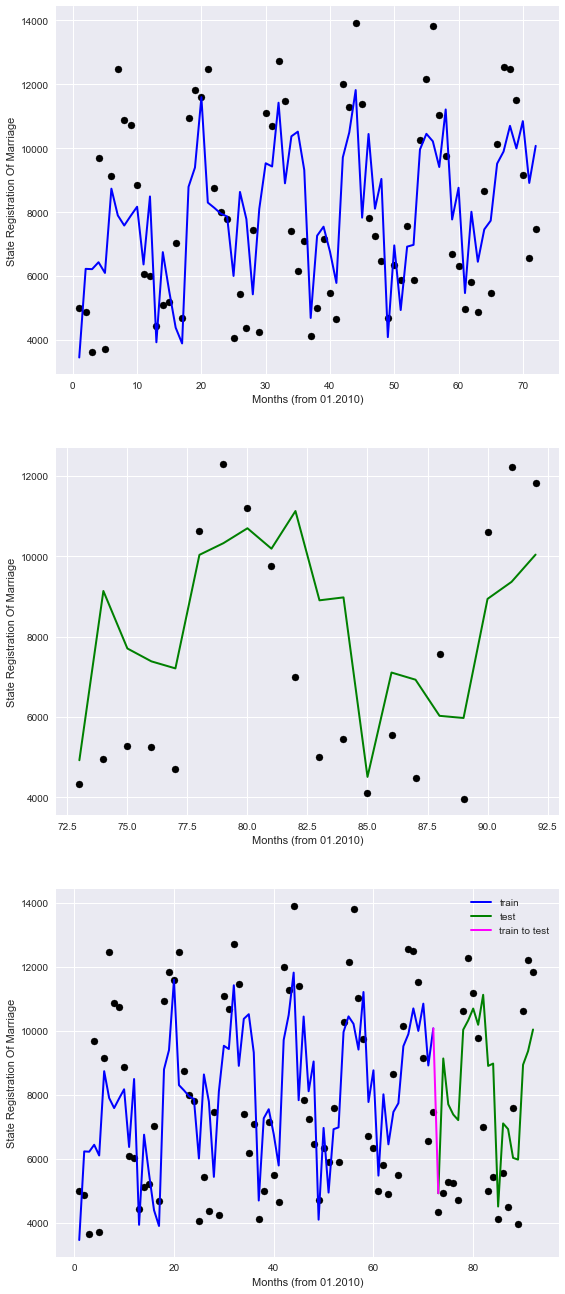
На графиках синим цветом представлено «прошлое», зеленым «будущее», а фиолетовым связка.
Итак, видно, что наша модель неидеально описывает точки, однако по крайней мере учитывает сезонные закономерности.
Таким образом, можно надеется, что и в будущем по имеющимся данным модель, сможет нас хоть как-то сориентировать, в части регистрации браков.
Хотя для анализа трендов есть, куда как более совершенные инструменты, которые выходят за рамки данной статьи (и на мой взгляд, начальных навыков в Data Science)
В завершении картинка, по мотивам общения Александра Григорьевича с журналистами и ответов на неудобные вопросы.

В последних статьях мы рассмотрели пару задачек по классификации, в процессе потом и кровью добывая себе данные, теперь пришло время регрессии. Поскольку ничего светотехнического в этот раз под рукой не оказалось, я решил поскрести по другим сусекам.
Помнится, в одной из статей я агитировал читателей посмотреть в сторону отечественных открытых данных. Но поскольку я не барышня из рекламы «кефирчика для пищеварения» или шампуня с лошадиной силой, совесть не позволяла советовать что-либо, не испытав на себе.
С чего начать? Конечно с открытых данных правительства РФ, там же ведь целое министерство есть. Мое знакомство с открытыми данными правительства РФ, было примерно, такое же как на иллюстрации к этой статье. Нет ну не то чтобы мне совсем не был интересен реестр Кинозалов города Новый Уренгой или перечень прокатного оборудования катка в Туле, просто для задачи регрессии они не очень подходят.
Если порыться думаю и на сайте ОД правительства РФ можно найти, что-то путное, просто не очень легко.
Данные Минфина я тоже решил оставить, на потом.
Пожалуй, больше всего мне понравились открытые данные правительства Москвы, там я присмотрел пару потенциальных задачек и выбрал в итоге Сведения о регистрации актов гражданского состояния в Москве по годам
Что вышло из применения минимальных навыков в области линейной регрессии можно в краткой форме посмотреть на GitHub, ну и конечно же заглянув под кат.

Введение
Как обычно, в начале статьи расскажу о навыках необходимых для понимания этой статьи.
От вас потребуется:
- Почитать самоучитель или пробежать простой обучающий курс по Машинному обучению
- Немного понимать Python
- Иметь практически нулевые знания в области математики
Если вы совсем новичок в области анализа данных и машинного обучения, посмотрите прошлые статьи цикла в порядке их следования, там каждая статья писалась по «горячим следам» и вы поймете стоит ли Вам тратить время на Data Science.
Все ранее подготовленные статьи ниже под спойлером
Другие статьи цикла
2. Практикуем первые навыки
1. Учим азы:
- «Ловись Data большая и маленькая!» — (Краткий обзор курсов по Data Science от Cognitive Class)
- «Теперь он и тебя сосчитал» или Наука о данных с нуля (Data Science from Scratch)
- «Айсберг вместо Оскара!» или как я пробовал освоить азы DataScience на kaggle
- ««Паровозик, который смог!» или «Специализация Машинное обучение и анализ данных», глазами новичка в Data Science
2. Практикуем первые навыки
Ну и как обещал раньше теперь статьи этого цикла будут комплектоваться содержанием.
Содержание:
Часть I: «Жениться — не лапоть надеть» — Получение и первичный анализ данных.
Часть II: «Один в поле не воин» — Регрессия по 1 признаку
Часть III: «Одна голова хорошо, а много лучше» — Регрессия по нескольким признакам с регуляризацией
Часть IV: «Не все то золото что блестит» — Добавляем признаки
Часть V: «Крой новый кафтан, а к старому примеряй!» — Прогноз тренда
Итак, перейдем подробней к задаче. Наша с Вами цель, откопать какой-нибудь набор данных достаточный для того, чтобы продемонстрировать основные приемы линейной регрессии и самим определить, что мы будем прогнозировать.
В этот раз буду краток и не буду отходить от темы рассмотрев только линейную регрессию (вы же наверняка знаете о существовании и других методов)
Часть I: «Жениться — не лапоть надеть» — Получение и первичный анализ данных
К сожалению, открытые данные правительства Москвы не настолько обширны и бескрайны как бюджет затраченный на благоустройство по программе «Моя улица», но тем не менее кое-что путное найти удалось.Динамика регистрации актов гражданского состояния, нам вполне подойдет.
Это почти сотня записей, разбитых по месяцам, в которых есть данные о количестве свадеб, рождений, установление родительства, смертей, смен имен и т.д.
Для решения задачи регрессии вполне подойдет.
Весь код целиком, размещен на GitHub
Ну а по частям мы его препарируем прямо сейчас.
Для начала импортируем библиотеки:
import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import numpy as np from sklearn.preprocessing import MinMaxScaler from sklearn.model_selection import train_test_split from sklearn import linear_model import warnings warnings.filterwarnings('ignore') %matplotlib inline Затем загрузим данные. Библиотека Pandas позволяет загружать файлы с удаленного сервера, что в общем и целом просто замечательно, при условии, конечно что на портале не изменится алгоритм переадресации страниц.
(надеюсь, что ссылка на скачивание в коде, не накроется, если она перестанет работать пожалуйста напишите в «личку», чтобы я мог обновить)
#download df = pd.read_csv('https://op.mos.ru/EHDWSREST/catalog/export/get?id=230308', compression='zip', header=0, encoding='cp1251', sep=';', quotechar='"') #look at the data df.head(12) Посмотрим на данные:
| ID | global_id | Year | Month | StateRegistrationOfBirth | StateRegistrationOfDeath | StateRegistrationOfMarriage | StateRegistrationOfDivorce | StateRegistrationOfPaternityExamination | StateRegistrationOfAdoption | StateRegistrationOfNameChange | TotalNumber |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 37591658 | 2010 | январь | 9206 | 10430 | 4997 | 3302 | 1241 | 95 | 491 | 29762 |
| 2 | 37591659 | 2010 | февраль | 9060 | 9573 | 4873 | 2937 | 1326 | 97 | 639 | 28505 |
| 3 | 37591660 | 2010 | март | 10934 | 10528 | 3642 | 4361 | 1644 | 147 | 717 | 31973 |
| 4 | 37591661 | 2010 | апрель | 10140 | 9501 | 9698 | 3943 | 1530 | 128 | 642 | 35572 |
| 5 | 37591662 | 2010 | май | 9457 | 9482 | 3726 | 3554 | 1397 | 96 | 492 | 28204 |
| 6 | 62353812 | 2010 | июнь | 11253 | 9529 | 9148 | 3666 | 1570 | 130 | 556 | 35852 |
| 7 | 62353813 | 2010 | июль | 11477 | 14340 | 12473 | 3675 | 1568 | 123 | 564 | 44220 |
| 8 | 62353814 | 2010 | август | 10302 | 15016 | 10882 | 3496 | 1512 | 134 | 578 | 41920 |
| 9 | 62353816 | 2010 | сентябрь | 10140 | 9573 | 10736 | 3738 | 1480 | 101 | 686 | 36454 |
| 10 | 62353817 | 2010 | октябрь | 10776 | 9350 | 8862 | 3899 | 1504 | 89 | 687 | 35167 |
| 11 | 62353818 | 2010 | ноябрь | 10293 | 9091 | 6080 | 3923 | 1355 | 97 | 568 | 31407 |
| 12 | 62353819 | 2010 | декабрь | 10600 | 9664 | 6023 | 4145 | 1556 | 124 | 681 | 32793 |
Если мы хотим пользоваться данными о месяцах, их необходимо перевести в понятный модели формат, у scikit-learn есть свои методы, но мы для надежности сделаем руками (ибо не очень много работы) ну и заодно удалим пару бесполезных в нашем случае столбцов с ID и мусором.
#code months d={'январь':1, 'февраль':2, 'март':3, 'апрель':4, 'май':5, 'июнь':6, 'июль':7, 'август':8, 'сентябрь':9, 'октябрь':10, 'ноябрь':11, 'декабрь':12} df.Month=df.Month.map(d) #delete some unuseful columns df.drop(['ID','global_id','Unnamed: 12'],axis=1,inplace=True) #look at the data df.head(12) Поскольку я не уверен, что табличный вид у всех откроется нормально посмотрим на данные с помощью картинки.
 Построим парные диаграммы, из которых будет понятно, какие столбцы нашей таблицы, линейно зависят друг от друга. Однако сразу все данные мы не будем рассматривать, чтобы потом было, что добавить, поэтому вначале уберем часть данных.
Построим парные диаграммы, из которых будет понятно, какие столбцы нашей таблицы, линейно зависят друг от друга. Однако сразу все данные мы не будем рассматривать, чтобы потом было, что добавить, поэтому вначале уберем часть данных.Достаточно простой способ выделить(«удалить») часть столбцов из pandas Dataframe, это просто сделать выборку по нужным столбцам:
columns_to_show = ['StateRegistrationOfBirth', 'StateRegistrationOfMarriage', 'StateRegistrationOfPaternityExamination', 'StateRegistrationOfDivorce','StateRegistrationOfDeath'] data=df[columns_to_show] Ну а теперь можно и график построить.
grid = sns.pairplot(data) 
Хорошей практикой является масштабирование признаков, чтобы не сравнивать лошадей с весом копны сена и средним атмосферным давлением в течении месяца.
В нашем случае все данные представлены в одних величинах (количестве зарегистрированных актов), но давайте все же посмотрим, что изменит масштабирование.
# change scale of features scaler = MinMaxScaler() df2=pd.DataFrame(scaler.fit_transform(df)) df2.columns=df.columns data2=df2[columns_to_show] grid2 = sns.pairplot(data2) 
Почти ничего, но для надежности пока будем брать масштабированные данные.
Часть II: «Один в поле не воин» — Регрессия по 1 признаку
Посмотрим на картинки и увидим, что лучше всего прямой линией можно описать связь между двумя признаками StateRegistrationOfBirth и StateRegistrationOfPaternityExamination, что в общем и не сильно удивляет (чем чаще проверяют «отцовство», тем чаще регистрируют детей).Подготовим данные, а именно выделим два столбца признак и целевую функцию, затем с помощью готовых библиотек поделим данные на обучающую и контрольную выборку (манипуляции в конце кода были нужны, для приведения данных к нужной форме)
X = data2['StateRegistrationOfBirth'].values y = data2['StateRegistrationOfPaternityExamination'].values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42) X_train=np.reshape(X_train,[X_train.shape[0],1]) y_train=np.reshape(y_train,[y_train.shape[0],1]) X_test=np.reshape(X_test,[X_test.shape[0],1]) y_test=np.reshape(y_test,[y_test.shape[0],1]) Важно отметить, что сейчас несмотря на явную возможность привязаться к хронологии, мы в целях демонстрации рассмотрим данные просто как набор записей без привязки ко времени.
«Скормим» наши данные модели и посмотрим на коэффициент при нашем признаке, а также оценим точность подгонки модели с помощью R^2 (коэффициент детерминации).
#teach model and get predictions lr = linear_model.LinearRegression() lr.fit(X_train, y_train) print('Coefficients:', lr.coef_) print('Score:', lr.score(X_test,y_test)) Получилось не очень, с другой стороны сильно лучше чем если бы мы «тыкались на угад»
Coefficients: [[ 0.78600258]]
Score: 0.611493944197
Посмотрим это на графиках, вначале на обучающих данных:
plt.scatter(X_train, y_train, color='black') plt.plot(X_train, lr.predict(X_train), color='blue', linewidth=3) plt.xlabel('StateRegistrationOfBirth') plt.ylabel('State Registration OfPaternity Examination') plt.title="Regression on train data" 
А теперь на контрольных:
plt.scatter(X_test, y_test, color='black') plt.plot(X_test, lr.predict(X_test), color='green', linewidth=3) plt.xlabel('StateRegistrationOfBirth') plt.ylabel('State Registration OfPaternity Examination') plt.title="Regression on test data" 
Часть III: «Одна голова хорошо, а много лучше» — Регрессия по нескольким признакам с регуляризацией
Чтобы было интересней давайте выберем другую целевую функцию, которая не так очевидно линейно зависит от признаков.
Чтобы соответствовать названию статью, в качестве целевой функции выберем регистрацию браков.
А все остальные столбцы из набора с картинок парных диаграмм сделаем признаками.
#get main data columns_to_show2=columns_to_show.copy() columns_to_show2.remove("StateRegistrationOfMarriage") #get data for a model X = data2[columns_to_show2].values y = data2['StateRegistrationOfMarriage'].values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42) y_train=np.reshape(y_train,[y_train.shape[0],1]) y_test=np.reshape(y_test,[y_test.shape[0],1]) Обучим вначале просто модель линейной регрессии.
lr = linear_model.LinearRegression() lr.fit(X_train, y_train) print('Coefficients:', lr.coef_) print('Score:', lr.score(X_test,y_test)) Получим результат чуть хуже, чем в прошлом случае (что и не удивительно)
Coefficients: [[-0.03475475 0.97143632 -0.44298685 -0.18245718]]
Score: 0.38137432065
Для борьбы с переобучением и/или отбора признаков, вместе с моделью линейной регрессии обычно используют механизм регуляризации, в данной статьи мы рассмотрим механизм Lasso (L1 – regularization)
Чем больше коэффициент регуляризации альфа, тем активнее модель штрафует большие значения признаков, вплоть до приведения некоторых коэффициентов уравнения регрессии к нулю.
#let's look at the different alpha parameter: #large Rid=linear_model.Lasso (alpha = 0.01) Rid.fit(X_train, y_train) print(' Appha:', Rid.alpha) print(' Coefficients:', Rid.coef_) print(' Score:', Rid.score(X_test,y_test)) #Small Rid=linear_model.Lasso (alpha = 0.000000001) Rid.fit(X_train, y_train) print(' Appha:', Rid.alpha) print(' Coefficients:', Rid.coef_) print(' Score:', Rid.score(X_test,y_test)) #Optimal (for these test data) Rid=linear_model.Lasso (alpha = 0.00025) Rid.fit(X_train, y_train) print(' Appha:', Rid.alpha) print(' Coefficients:', Rid.coef_) print(' Score:', Rid.score(X_test,y_test)) Надо отметить, что тут я делаю прям вот нехорошие вещи, подогнал коэффициент регуляризации под тестовые данные, в реальности так делать не стоит, но нам чисто для демонстрации сойдет.
Посмотрим на вывод:
Appha: 0.01
Coefficients: [ 0. 0.46642996 -0. -0. ]
Score: 0.222071102783
Appha: 1e-09
Coefficients: [-0.03475462 0.97143616 -0.44298679 -0.18245715]
Score: 0.38137433837
Appha: 0.00025
Coefficients: [-0.00387233 0.92989507 -0.42590052 -0.17411615]
Score: 0.385551648602
В данном случае модель с регуляризацией не сильно повышает качество, попробуем добавить еще признаков.
Часть IV: «Не все то золото что блестит» — Добавляем признаки
Добавим очевидно бесполезный признак «общее количество регистраций», почему очевидно? Сейчас сами в этом убедитесь.columns_to_show3=columns_to_show2.copy() columns_to_show3.append("TotalNumber") columns_to_show3 X = df2[columns_to_show3].values # y hasn't changed X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42) y_train=np.reshape(y_train,[y_train.shape[0],1]) y_test=np.reshape(y_test,[y_test.shape[0],1]) Для начала посмотрим на результаты без регуляризации
lr = linear_model.LinearRegression() lr.fit(X_train, y_train) print('Coefficients:', lr.coef_) print('Score:', lr.score(X_test,y_test)) Coefficients: [[-0.45286477 -0.08625204 -0.19375198 -0.63079401 1.57467774]]
Score: 0.999173764473
С ума сойти! Почти 100% точность!
Как же этот признак можно было назвать бесполезным?!
Ну давайте мыслить здраво, наше количество браков входит в общее количество, поэтому если у нас есть сведения о других признаках, то и точность близится к 100%. На практике это не особо полезно.
Давайте перейдем к нашему «Лассо»
Вначале выберем небольшой коэффициент регуляризации:
#Optimal (for these test data) Rid=linear_model.Lasso (alpha = 0.00015) Rid.fit(X_train, y_train) print(' Appha:', Rid.alpha) print(' Coefficients:', Rid.coef_) print(' Score:', Rid.score(X_test,y_test)) Appha: 0.00015
Coefficients: [-0.44718703 -0.07491507 -0.1944702 -0.62034146 1.55890505]
Score: 0.999266251287
Ну ничего сильно не поменялось, это нам не интересно, давайте посмотрим, что будет если его увеличить.
#large Rid=linear_model.Lasso (alpha = 0.01) Rid.fit(X_train, y_train) print(' Appha:', Rid.alpha) print(' Coefficients:', Rid.coef_) print(' Score:', Rid.score(X_test,y_test)) Appha: 0.01
Coefficients: [-0. -0. -0. -0.05177979 0.87991931]
Score: 0.802210158982
Итак, видим, что почти все признаки были признаны моделью бесполезными, а самым полезным остался признак общего количества записей, так, что если бы нам вдруг пришлось использовать только 1-2 признака мы бы знали, что выбрать, чтобы минимизировать потери.
Давайте чисто из любопытства посмотрим как можно было объяснить процент регистрации браков только лишь общим количеством записей.
X_train=np.reshape(X_train[:,4],[X_train.shape[0],1]) X_test=np.reshape(X_test[:,4],[X_test.shape[0],1]) lr = linear_model.LinearRegression() lr.fit(X_train, y_train) print('Coefficients:', lr.coef_) print('Score:', lr.score(X_train,y_train)) Coefficients: [ 1.0571131]
Score: 0.788270672692
Ну что же неплохо, но объективно меньше, чем с учётом остальных признаков.
Давайте посмотрим на графики:
# plot for train data plt.figure(figsize=(8,10)) plt.subplot(211) plt.scatter(X_train, y_train, color='black') plt.plot(X_train, lr.predict(X_train), color='blue', linewidth=3) plt.xlabel('Total Number of Registration') plt.ylabel('State Registration Of Marriage') plt.title="Regression on train data" # plot for test data plt.subplot(212) plt.scatter(X_test, y_test, color='black') plt.plot(X_test, lr.predict(X_test), '--', color='green', linewidth=3) plt.xlabel('Total Number of Registration') plt.ylabel('State Registration Of Marriage') plt.title="Regression on test data"
Давайте попробуем к исходному набору данных теперь добавить другой бесполезный признак
State Registration Of Name Change (смену имени), можете самостоятельно построить модель и посмотреть, какую долю данных объясняет этот признак (маленькую поверьте на слово).
А мы сразу подберем данные и обучим модель на старых 4х признаках и этом бесполезном
columns_to_show4=columns_to_show2.copy() columns_to_show4.append("StateRegistrationOfNameChange") X = df2[columns_to_show4].values # y hasn't changed X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42) y_train=np.reshape(y_train,[y_train.shape[0],1]) y_test=np.reshape(y_test,[y_test.shape[0],1]) lr = linear_model.LinearRegression() lr.fit(X_train, y_train) print('Coefficients:', lr.coef_) print('Score:', lr.score(X_test,y_test)) Coefficients: [[ 0.06583714 1.1080889 -0.35025999 -0.24473705 -0.4513887 ]]
Score: 0.285094398157
Не будем пробовать регуляризацию она кардинально ничего не изменит, как видно данный признак нам все только портит.
Давайте наконец-то выберем полезный признак.
Все знают, что есть горячий сезон для свадеб (лето и начало осени), а есть тихий сезон (зима).
Меня кстати удивило, что в мае отмечают мало свадеб.
#get data columns_to_show5=columns_to_show2.copy() columns_to_show5.append("Month") #get data for model X = df2[columns_to_show5].values # y hasn't changed X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42) y_train=np.reshape(y_train,[y_train.shape[0],1]) y_test=np.reshape(y_test,[y_test.shape[0],1]) #teach model and get predictions lr = linear_model.LinearRegression() lr.fit(X_train, y_train) print('Coefficients:', lr.coef_) print('Score:', lr.score(X_test,y_test)) Coefficients: [[-0.10613428 0.91315175 -0.55413198 -0.13253367 0.28536285]]
Score: 0.472057997208
Неплохое повышение качества и главное все соответствует здравой логике.
Часть V: «Крой новый кафтан, а к старому примеряй!» — Прогноз тренда
Последнее что нам, пожалуй, осталось, это присмотреться к линейной регрессии как к инструменту для предсказания тренда. В прошлых главах мы брали данные случайно, то есть в обучающую выборку попадали данные из всего временного диапазона. В этот раз мы поделим данные на прошлое и будущее и посмотрим, удастся ли нам что-то предсказатьДля удобства будем считать срок в месяцах с января 2010, для этого напишем простую анонимную функцию, которая нам преобразует данные, в итоге заменим столбец год, на количество месяцев.
Обучаться будем на данных до 2016 года, а будущим для нас станет все что начинается с 2016 года.
#get data df3=df.copy() #get new column df3.Year=df.Year.map(lambda x: (x-2010)*12)+df.Month df3.rename(columns={'Year': 'Months'}, inplace=True) #get data for model X=df3[columns_to_show5].values y=df3['StateRegistrationOfMarriage'].values train=[df3.Months<=72] test=[df3.Months>72] X_train=X[train] y_train=y[train] X_test=X[test] y_test=y[test] y_train=np.reshape(y_train,[y_train.shape[0],1]) y_test=np.reshape(y_test,[y_test.shape[0],1]) #teach model and get predictions lr = linear_model.LinearRegression() lr.fit(X_train, y_train) print('Coefficients:', lr.coef_[0]) print('Score:', lr.score(X_test,y_test)) Coefficients: [ 2.60708376e-01 1.30751121e+01 -3.31447168e+00 -2.34368684e-01
2.88096512e+02]
Score: 0.383195050367
Как видно при такой разбивке данных, точность несколько снижается и тем не менее качество предсказания всяко лучше, чем пальцем в небо.
Убедимся посмотрев на графики.
plt.figure(figsize=(9,23)) # plot for train data plt.subplot(311) plt.scatter(df3.Months.values[train], y_train, color='black') plt.plot(df3.Months.values[train], lr.predict(X_train), color='blue', linewidth=2) plt.xlabel('Months (from 01.2010)') plt.ylabel('State Registration Of Marriage') plt.title="Regression on train data" # plot for test data plt.subplot(312) plt.scatter(df3.Months.values[test], y_test, color='black') plt.plot(df3.Months.values[test], lr.predict(X_test), color='green', linewidth=2) plt.xlabel('Months (from 01.2010)') plt.ylabel('State Registration Of Marriage') plt.title="Regression (prediction) on test data" # plot for all data plt.subplot(313) plt.scatter(df3.Months.values[train], y_train, color='black') plt.plot(df3.Months.values[train], lr.predict(X_train), color='blue', label='train', linewidth=2) plt.scatter(df3.Months.values[test], y_test, color='black') plt.plot(df3.Months.values[test], lr.predict(X_test), color='green', label='test', linewidth=2) plt.title="Regression (prediction) on all data" plt.xlabel('Months (from 01.2010)') plt.ylabel('State Registration Of Marriage') #plot line for link train to test plt.plot([72,73], lr.predict([X_train[-1],X_test[0]]) , color='magenta',linewidth=2, label='train to test') plt.legend() 
На графиках синим цветом представлено «прошлое», зеленым «будущее», а фиолетовым связка.
Итак, видно, что наша модель неидеально описывает точки, однако по крайней мере учитывает сезонные закономерности.
Таким образом, можно надеется, что и в будущем по имеющимся данным модель, сможет нас хоть как-то сориентировать, в части регистрации браков.
Хотя для анализа трендов есть, куда как более совершенные инструменты, которые выходят за рамки данной статьи (и на мой взгляд, начальных навыков в Data Science)
Заключение
Ну вот мы и рассмотрели задачу восстановления регрессии, предлагаю вам поискать и другие зависимости, на порталах открытых данных государственных структур страны, возможно вы найдете какую-нибудь интересную зависимость. В качестве «челенджа» предлагаю, вам откопать, что-нибудь на портале открытых данных Республики Беларусь opendata.byВ завершении картинка, по мотивам общения Александра Григорьевича с журналистами и ответов на неудобные вопросы.

Источник: habrahabr.ru