PyTorch — ваш новый фреймворк глубокого обучения

PyTorch — современная библиотека глубокого обучения, развивающаяся под крылом Facebook. Она не похожа на другие популярные библиотеки, такие как Caffe, Theano и TensorFlow. Она позволяет исследователям воплощать в жизнь свои самые смелые фантазии, а инженерам с лёгкостью эти фантазии имплементировать.

Данная статья представляет собой лаконичное введение в PyTorch и предназначена для быстрого ознакомления с библиотекой и формирования понимания её основных особенностей и её местоположения среди остальных библиотек глубокого обучения.

PyTorch является аналогом фреймворка Torch7 для языка Python. Разработка его началась в недрах Facebook ещё в 2012 году, всего на год позже появления самого Torch7, но открытым и доступным широкой публике PyTorch стал лишь в 2017 году. С этого момента фреймворк очень быстро набирает популярность и привлекает внимание всё большего числа исследователей. Что же делает его таким популярным?

Место среди остальных фреймворков

Для начала разберёмся, что же вообще такое фреймворк глубокого обучения. Под глубоким обучением как правило понимают обучение функции, представляющей собой композицию множества нелинейных преобразований. Такая сложная функция ещё называется потоком или графом вычислений. Фреймворк глубокого обучения должен уметь делать всего три вещи:

1. Определять граф вычислений;
2. Дифференцировать граф вычислений;
3. Вычислять его.

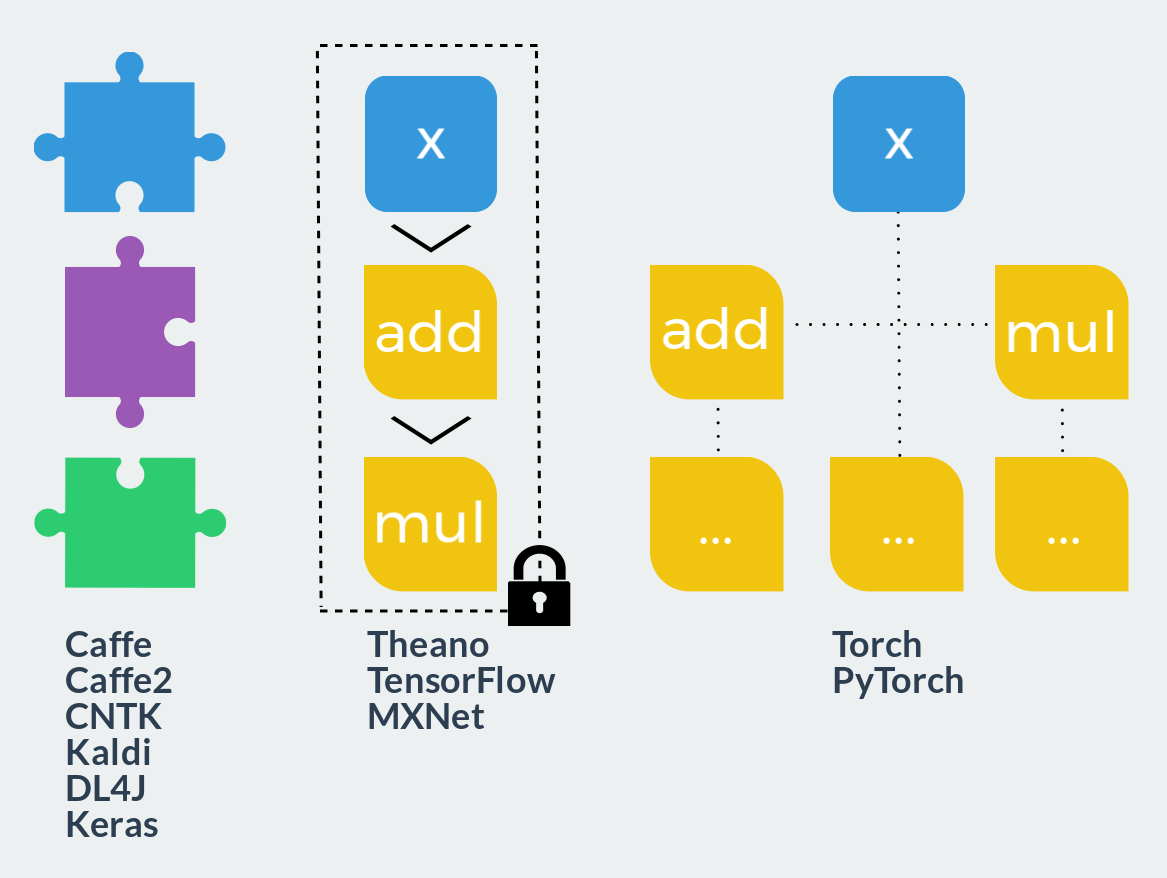
Чем быстрее ты умеешь вычислять свою функцию и чем гибче твои возможности для её определения, тем лучше. Сейчас, когда каждый фреймворк умеет использовать всю мощь видеокарт, первый критерий перестал играть значительную роль. Что нас действительно интересует, так это доступные возможности для определения потока вычислений. Все фреймворки здесь можно разделить на три крупные категории.

• Фиксированные модули. Такой подход можно сравнить с конструктором Lego: пользователь комбинирует заранее определённые блоки в граф вычислений и запускает его. Прямой и обратный проходы уже зашиты в каждом таком блоке. Определение новых блоков гораздо сложнее использования готовых и требует совершенно иных знаний и умений. Расширяемость близка к нулю, однако если ваши идеи полностью реализуются в таком фреймворке, скорость разработки максимальна. Со скоростью работы, благодаря высокой оптимизированности заранее написанного кода, также не возникает проблем. Типичные представители: Caffe, Caffe2, CNTK, Kaldi, DL4J, Keras (как интерфейс).
• Статический граф вычислений. Эти фреймворки уже можно сравнить с полимерной глиной: на этапе описания возможно создать граф вычислений произвольного размера и сложности, однако после запекания (компиляции) он станет твёрдым и монолитным. Доступными останутся всего два действия: запустить граф в прямом или обратном направлениях. Все такие фреймворки используют декларативный стиль программирования и напоминают функциональный язык или математическую нотацию. С одной стороны, этот подход комбинирует гибкость на этапе разработки и скорость в момент исполнения. С другой стороны, как и в функциональных языках, отладка становится настоящей головной болью, а модели, выходящие за рамки парадигмы, требуют либо титанических усилий, либо здоровенных костылей для реализации. Представители: Theano, TensorFlow, MXNet.
• Динамический граф вычислений. Представьте теперь, что вы можете перестраивать статический граф перед каждым его запуском. Примерно это и происходит в данном классе фреймворков. Только графа как отдельной сущности здесь нет. Он, как и в императивных языках программирования, слишком сложен для явного построения и существует лишь в в момент исполнения. Точнее сказать, граф строится динамически каждый раз при прямом проходе для того, чтобы затем иметь возможность сделать проход обратный. Подобный подход даёт максимальную гибкость и расширяемость, позволяет использовать в вычислениях все возможности используемого языка программирования и не ограничивает пользователя вообще ничем. К этому классу фреймворков как раз и относятся Torch и PyTorch.

Уверен, многие из нас начинали разбираться с глубоким обучением, используя только NumPy. Прямой проход написать на нём тривиально, а формулу обновления весов можно посчитать на листочке или вообще получить готовые веса из астрала. Выглядеть такой первый код мог так:

 import numpy as np  def MyNetworkForward(weights, bias, x):     h1 = weights @ x + bias     a1 = np.tanh(h1)      return a1  y = MyNetworkForward(weights, bias, x) loss = np.mean((y - y_hat) ** 2)

Со временем архитектуры сетей становятся сложнее и глубже и возможностей NumPy, карандаша и бумаги уже перестаёт не хватать. Если ваше соединение с астралом к этому моменту ещё не закрылось и вам есть откуда брать веса, вам повезло. В противном же случае невольно начинаешь задумываться о двух вещах:

1. Вот бы уметь запускать мои вычисления на видеокарте;
2. Вот бы все градиенты считались за меня.

При этом не хочется менять привычный подход, хочется просто написать:

 import numpy as np  def MyNetworkForward(weights, bias, x):     h1 = weights @ x + bias     a1 = np.tanh(h1)      return a1  weights.cuda() bias.cuda() x.cuda()  y = MyNetworkForward(weights, bias, x) loss = np.mean((y - y_hat) ** 2)  loss.magically_calculate_backward_pass()

Ну так вот, угадайте что? PyTorch ровно это и делает! Вот совершенно правильный код:

 import torch  def MyNetworkForward(weights, bias, x):     h1 = weights @ x + bias     a1 = torch.tanh(h1)      return a1  weights.cuda() bias.cuda() x.cuda()  y = MyNetworkForward(weights, bias, x) loss = torch.mean((y - y_hat) ** 2)  loss.backward()

Остаётся лишь применить уже посчитанные обновления параметров.

В Theano и TensorFlow мы описываем граф на декларативном DSL, который затем компилируется в некоторый внутренний байткод и исполняется в монолитном ядре, написанном на C++, или же компилируется в код на C и исполняется как отдельный бинарный объект. Если в момент компиляции нам известен весь граф целиком, его с лёгкостью можно продифференцировать, например символьно. Однако так ли необходима стадия компиляции?

Оказывается, нет. Ничто не мешает нам строить граф динамически одновременно с его вычислением! А благодаря технике автоматического дифференцирования (automatic differentiation, AD) мы можем взять и продифференцировать граф в любой момент времени в любом его состоянии. В компиляции графа нет совершенно никакой реальной необходимости. Что касается скорости, вызов лёгких нативных процедур из интерпретатора Python оказывается не медленнее, чем исполнение скомпилированного кода.

Не ограниченные DSL и компиляцией, мы можем использовать все возможности Python и делать код по-настоящему динамическим. Например, применять различные функции активации по чётным и нечётным дням:

 from datetime import date import torch.nn.functional as F  ... if date.today().day % 2 == 0:     x = F.relu(x) else:     x = F.linear(x) ...

Или мы можем создать слой, который каждый раз прибавляет к тензору только что введённое пользователем значение:

...  x += int(input()) ...

Более полезный пример я покажу в конце статьи. Резюмируя, всё сказанное выше можно выразить следующей формулой:
PyTorch = NumPy + CUDA + AD.

Тензорные вычисления

Начнём с NumPy части. Тензорные вычисления — основа PyTorch, каркас, вокруг которого наращивается вся остальная функциональность. К сожалению, нельзя сказать, что мощь и выразительность библиотеки в данном аспекте совпадает с таковой у NumPy. Во всём, что касается работы с тензорами, PyTorch руководствуется принципом максимальной простоты и прозрачности, предоставляя тонкую обёртку над вызовами BLAS.

Тензоры

Тип данных, хранимых тензором, отражается в имени его конструктора. Конструктор без параметров вернёт специальное значение — тензор без размерности, который нельзя использовать ни в каких операциях.

>>>  torch.FloatTensor() [torch.FloatTensor with no dimension]

Все возможные типы:

 torch.HalfTensor      # 16 бит, с плавающей точкой torch.FloatTensor     # 32 бита,  с плавающей точкой torch.DoubleTensor    # 64 бита, с плавающей точкой  torch.ShortTensor     # 16 бит, целочисленный, знаковый torch.IntTensor       # 32 бита, целочисленный, знаковый torch.LongTensor      # 64 бита, целочисленный, знаковый  torch.CharTensor      # 8 бит, целочисленный, знаковый torch.ByteTensor      # 8 бит, целочисленный, беззнаковый

Никакого автоматического определения типа или типа по-умолчанию не существует. torch.Tensor является сокращённым названием для torch.FloatTensor.

Автоматического приведения типов как в NumPy также не осуществляется:

>>>  a = torch.FloatTensor([1.0]) >>> b = torch.DoubleTensor([2.0]) >>> a * b

 TypeError: mul received an invalid combination of arguments - got (torch.DoubleTensor), but expected one of:  * (float value)       didn't match because some of the arguments have invalid types: (torch.DoubleTensor)  * (torch.FloatTensor other)       didn't match because some of the arguments have invalid types: (torch.DoubleTensor)

В этом плане PyTorch строже и безопаснее: вы не наткнётесь на двукратное увеличение потребляемой памяти, перепутав тип константы. Явное приведение типов доступно с помощью методов с соответствующими названиями.

>>>  a = torch.IntTensor([1]) >>> a.byte()   1 [torch.ByteTensor of size 1]  >>> a.float()   1 [torch.FloatTensor of size 1] 

x.type_as(y) вернёт тензор значений из x того же типа, что и y.

Любое приведение тензора к своему собственному типу не копирует его.

Если передать конструктору тензора в качестве параметра список, будет построен тензор соответствующей размерности и с соответствующими данными.

>>>  a = torch.IntTensor([[1, 2], [3, 4]]) >>> a   1  2  3  4 [torch.IntTensor of size 2x2]

Неправильно сформированные списки не допускаются так же, как и в NumPy.

>>>  torch.IntTensor([[1, 2], [3]])

 RuntimeError: inconsistent sequence length at index (1, 1) - expected 2 but got 1

Допускается построение тензора из значения любого типа последовательности, что весьма интуитивно и соответствует поведению NumPy.

Другой возможный набор аргументов конструктора тензора — его размер. Количество аргументов при этом определяет размерность.

Построенный таким методом тензор содержит мусор — случайные значения.

>>>  torch.FloatTensor(1)  1.00000e-17 *  -7.5072 [torch.FloatTensor of size 1]

>>>  torch.FloatTensor(3, 3)  -7.5072e-17  4.5909e-41 -7.5072e-17  4.5909e-41 -5.1601e+16  3.0712e-41  0.0000e+00  4.5909e-41  6.7262e-44 [torch.FloatTensor of size 3x3]

Индексирование

Поддерживается стандартное индексирование Python: обращение по индексу и срезы.

>>>  a = torch.IntTensor([[1, 2, 3], [4, 5, 6]]) >>> a   1  2  3  4  5  6 [torch.IntTensor of size 2x3]

>>>  a[0]   1  2  3 [torch.IntTensor of size 3]

>>>  a[0][1] 2 >>> a[0, 1] 2

>>>  a[:, 0]   1  4 [torch.IntTensor of size 2]  >>> a[0, 1:3]   2  3 [torch.IntTensor of size 2]

Также в качестве индексов могут выступать другие тензоры. Однако, возможности здесь всего две:

• Одномерный torch.LongTensor, индексирующий по нулевому измерению (по элементам в случае векторов и по строкам в случае матриц);
• Соразмерный torch.ByteTensor, содержащий только значения 0 или 1, служащий маской.

>>>  a = torch.ByteTensor(3,4).random_() >>> a    26  119  225  238   83  123  182   83  136    5   96   68 [torch.ByteTensor of size 3x4]  >>> a[torch.LongTensor([0, 2])]    81  218   40  131  144   46  196    6 [torch.ByteTensor of size 2x4]

>>>  a > 128   0  1  0  1  0  0  1  0  1  0  1  0 [torch.ByteTensor of size 3x4]  >>> a[a > 128]   218  131  253  144  196 [torch.ByteTensor of size 5]

Всю доступную информацию о тензоре помогут узнать функции x.dim(), x.size() и x.type(). x.data_pt() укажет на место в памяти, где находятся данные.

>>>  a = torch.Tensor(3, 3) >>> a.dim() 2 >>> a.size() torch.Size([3, 3]) >>> a.type() 'torch.FloatTensor' >>> a.data_ptr() 94124953185440

Операции над тензорами

Соглашение о именовании в PyTorch гласит, что любая функция вида xxx возвращает новый тензор, т.е. является immutable функцией. В противоположность ей функция вида xxx_ изменяет изначальный тензор, т.е. является mutable функцией. Последние ещё носят название inplace функций.

Почти для любой immutable функции в PyTorch существует её менее чистый собрат. Однако бывает и так, что функция существует лишь в каком-то одном варианте. По понятным причинам, функции, изменяющие размер тензора всегда являются immutable.

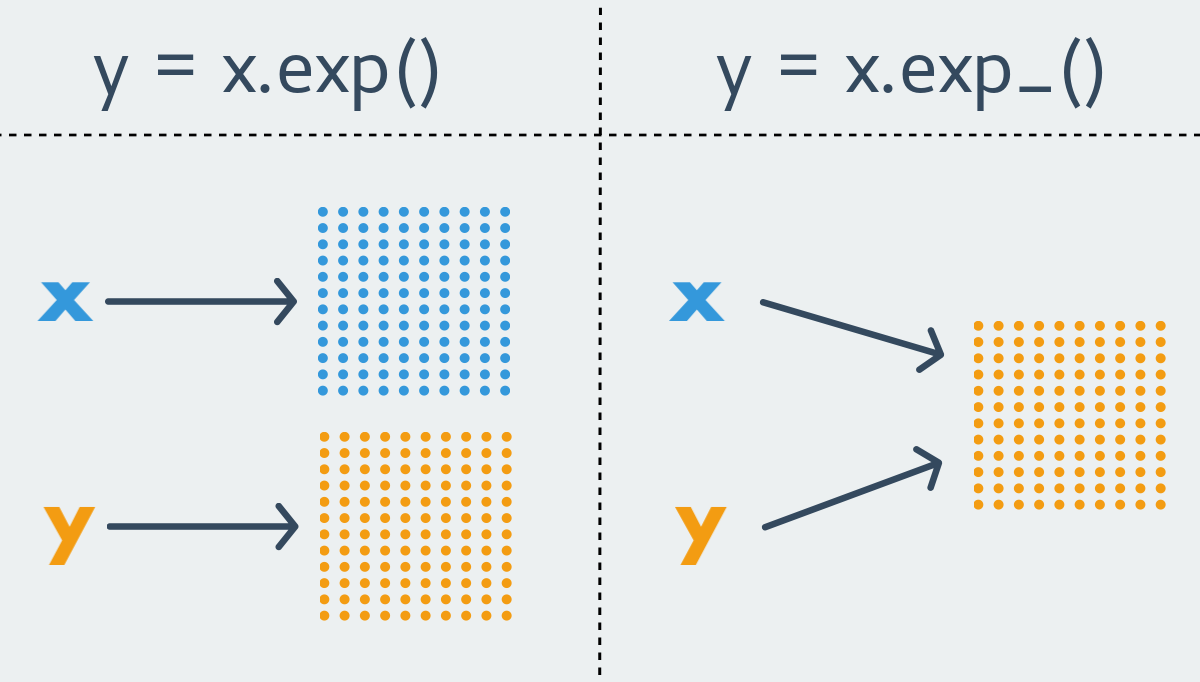
Перечислять все доступные операции над тензорами я не буду, остановлюсь лишь на самых важных и разделю их на категории.

Функции инициализации

Как правило, они используются для инициализации при создании новых тензоров заданного размера

 x = torch.FloatTensor(3, 4)   # мусор x.zero_()                     # нули

Так как mutable функции возвращают ссылку на объект, удобнее записывать объявление и инициализацию в одну строчку.

 x = torch.FloatTensor(3, 4).zero_()

• x.zero_()
  Инициализирует вектор нулями. Не имеет immutable варианта.
• x.fill_(n)
  Заполняет тензор константой n. Аналогично не имеет immutable варианта.
• x.random_(from, to)
  Заполняет тензор сэмплами из дискретного (даже для вещественнозначных тензоров) равномерного распределения.
  

  Если from и to не указаны, то они приравниваются нижней и верхней границам используемого типа данных соответственно.
  

• x.uniform_(from=0, to=1)
  Тоже равномерное распределение, но уже непрерывное и с более привычными границами по-умолчанию. Доступно только для вещественнозначных тензоров.
• x.normal_(mean=0, std=1)
  Нормальное распределение. Доступно только для вещественнозначных тензоров.
• x.bernoulli_(p=0.5)
  Распределение Бернулли. В качестве p может использоваться скаляр либо тензор той же размерности со значениями 0 <= p <= 1. Важно отличать эту версию от immutable варианта, так как он имеет другую семантику. Вызов y = x.bernoulli() эквивалентен y.bernoulli_(x), т.е. x здесь сам используется как тензор параметров распределения.
• torch.eye(n, m)
  Создаёт единичную матрицу n x m. Здесь по неясным для меня причинам не существует уже inplace варианта.

Доступны также экспоненциальное и геометрическое распределения, распределение Коши, логарифм нормального распределения и ещё несколько более сложных вариантов инициализации тензора. Не стесняйтесь смотреть в документацию!

Математические операции

Самая часто используемая группа. Если операция здесь не изменяет размер и тип тензора, то у неё существует inplace вариант.

• z = x.add(y)
z = torch.add(x, y)
x.add_(y)
  Сложение.
• z = x.sub(y)
z = torch.sub(x, y)
x.sub_(y)
  Вычитаение.
• z = x.mul(y)
z = torch.mul(x, y)
x.mul_(y)
  Умножение.
• z = x.div(y)
z = torch.div(x, y)
x.div_(y)
  Деление. Для целочисленных типов деление целочисленное.
• z = x.exp()
z = torch.exp(x)
x.exp_()
  Экспонента.
• z = x.log()
z = torch.log(x)
x.log_()
  Натуральный логарифм.
• z = x.log1p()
z = torch.log1p(x)
x.log1p_()
  Натуральный логарифм от x + 1. Функция оптимизирована по точности вычислений для малых x.
• z = x.abs()
z = torch.abs(x)
x.abs_()
  Модуль.

Естественно, присутствуют все основные тригонометрические операции в том виде, в каком вы ожидаете их увидеть. Перейдём теперь к менее тривиальным функциям.

• z = x.t()
z = torch.t(x)
x.t_()
  Транспонирование. Несмотря на то, что размер тензора меняется, существует inplace вариант функции, так как размер данных в памяти остаётся тем же.
• z = x.mm(y)
z = torch.mm(x, y)
  Матричное умножение.
• z = x.mv(v)
z = torch.mv(x, v)
  Умножение матрицы на вектор.
• z = x.dot(y)
z = torch.dot(x, y)
  Скалярное умножение тензоров.
• bz = bx.bmm(by)
bz = torch.bmm(bx, by)
  Перемножает матрицы целыми батчами.
  

  >>>  bx = torch.randn(10, 3, 4) >>> by = torch.randn(10, 4, 5) >>> bz = bx.bmm(bz) >>> bz.size() torch.Size([10, 3, 5])

Существуют также полные аналоги BLAS функций со сложными сигнатурами, такие как addbmm, addmm, addmv, addr, baddbmm, btrifact, btrisolve, eig, gels и множество других.

Операции редукции похожи друг на друга по сигнатуре. Почти все они своим последним необязательным аргументом принимают dim — размерность, по которой редукция проводится. Если аргумент не задан, операция действует на весь тензор целиком.

• s = x.mean(dim)
s = torch.mean(x, dim)
  Выборочное среднее. Определена только для вещественнозначных тензоров.
• s = x.std(dim)
s = torch.std(x, dim)
  Выборочное стандартное отклонение. Определена только для вещественнозначных тензоров.
• s = x.var(dim)
s = torch.var(x, dim)
  Выборочная дисперсия. Определена только для вещественнозначных тензоров.
• s = x.median(dim)
s = torch.median(x, dim)
  Медиана.
• s = x.sum(dim)
s = torch.sum(x, dim)
  Сумма.
• s = x.prod(dim)
s = torch.prod(x, dim)
  Произведение.
• s = x.max(dim)
s = torch.max(x, dim)
  Максимум.
• s = x.min(dim)
s = torch.min(x, dim)
  Минимум.

Всевозможные операции сравнения ( eq, ne, gt, lt, ge, le) также определены и возвращают в качестве результата своей работы маску типа ByteTensor .

Операторы +, +=, -, -=, *, *=, /, /=, @ работают ровно так, как вы и ожидаете, вызывая соответствующие описанные выше функции. Однако из-за сложности и не полной очевидности API, я не рекомендую пользоваться операторами, а использовать вместо этого явный вызов нужных функций. По крайней мере не стоит смешивать два стиля, это позволит избежать ошибок навроде x += x.mul_(2).

У PyTorch в запасе ещё много интересных функций вроде сортировки или поэлементного применения функции, но все они крайне редко используются в глубоком обучении. Если же вы захотите использовать PyTorch в качестве библиотеки тензорных вычислений, не забудьте перед этим заглянуть в документацию.

Broadcasting

Broadcasting — сложная тема. На мой взгляд, лучше бы его не было. Но он есть, хотя и появился лишь в одном из последних релизов. Многие операции в PyTorch теперь поддерживают broadcasting в привычном NumPy стиле.

Если говорить в общем, то два непустых тензора называются bradcastable, если, начиная с последнего измерения, размеры обоих тензоров в этом измерении либо равны, либо размер одного из них равен единице, либо измерений в тензоре больше не существует. Легче понять на примерах.

>>>  x = torch.FloatTensor(5, 7, 3) >>> y = torch.FloatTensor(5, 7, 3) # bradcatable, тривиальный случай: все размеры, начиная с последнего измерения, равны

>>>  x = torch.FloatTensor(5, 3, 4, 1) >>> y = torch.FloatTensor(   3, 1, 1) # bradcatable, размер по последнему измерению равен, по предпоследнему измерению у второго тензора размер равен единице, по второму измерению размеры равны, а дальше измерения у второго тензора заканчиваются

>>>  x = torch.FloatTensor(5, 2, 4, 1) >>> y = torch.FloatTensor(   3, 1, 1) # не bradcatable, размер по второму измерению не равен (2 != 3) и при этом ни один из этих размеров не равен единице

>>>  x = torch.FloatTensor() >>> y = torch.FloatTensor(2, 2) # не bradcatable, у x нет хотя бы одного (последнего) измерения

Тензор размерности torch.Size([1]), будучи скаляром, очеидным образом broadcastable с любым другим тензором.

Размер тензора, получившегося в результате broadcasting, расчитывается следующим образом:

1. Если количество измерений у тензоров не равно, то там, где это необходимо, добавляются единицы.
2. Затем размер получившегося тензора расчитывается как поэлементный максимум исходных тензоров.

>>>  x = torch.FloatTensor(5, 1, 4, 1) >>> y = torch.FloatTensor(   3, 1, 1) >>> (x+y).size() torch.Size([5, 3, 4, 1])

В примере размерность второго тензора была дополнена единицей в начале, а затем поэлементный максимум определил размерность результирующего тензора.

Подвох кроется в inplace операциях. Broadcasting для них разрешён лишь в том случае, когда размер исходного тензора не изменится.

>>>  x = torch.FloatTensor(5, 3, 4, 1) >>> y = torch.FloatTensor(   3, 1, 1) >>> (x.add_(y)).size() torch.Size([5, 3, 4, 1])

>>>  x=torch.FloatTensor(1, 3, 1) >>> y=torch.FloatTensor(3, 1, 7) >>> (x.add_(y)).size()

 RuntimeError: The expanded size of the tensor (1) must match the existing size (7) at non-singleton dimension 2.

Во втором случае тензоры очевидно broadcastable, однако inplace операция не разрешена, поскольку x в ходе неё изменил бы размер.

Из NumPy и обратно

Функции torch.from_numpy(n) и x.numpy() могут быть использованы, чтобы конвертировать тензоры одной библиотеки в тензоры другой.

Тензоры при этом используют одно и то же внутренне хранилище, копирования данных не происходит.

>>>  import torch >>> import numpy as np >>> a = np.random.rand(3, 3) >>> a array([[ 0.3191423 ,  0.75283128,  0.31874139],        [ 0.0077988 ,  0.66912423,  0.3410516 ],        [ 0.43789109,  0.39015864,  0.45677317]]) >>> b = torch.from_numpy(a) >>> b   0.3191  0.7528  0.3187  0.0078  0.6691  0.3411  0.4379  0.3902  0.4568 [torch.DoubleTensor of size 3x3]  >>> b.sub_(b)   0  0  0  0  0  0  0  0  0 [torch.DoubleTensor of size 3x3]  >>> a array([[ 0.,  0.,  0.],        [ 0.,  0.,  0.],        [ 0.,  0.,  0.]])

На этом все основные моменты тензорной библиотеки PyTorch предлагаю считать рассмотренными. Надеюсь, теперь читателю понятно, что реализовать прямой проход для произвольной функции на PyTorch ничуть не сложнее, чем сделать это с помощью NumPy. Нужно лишь свыкнуться с inplace операциями и запомнить имена основных функций. Для примера, линейный слой с функцией активации softmax:

 def LinearSoftmax(x, w, b):     s = x.mm(w).add_(b)     s.exp_()     s.div_(s.sum(1))      return s

CUDA

Здесь всё просто: тензоры могут жить либо "на процессоре", либо "на видеокарте". Правда, они весьма привередливы и живут только на видеокартах от Nvidia, причём не на самых старых. По-умолчанию тензор создаётся на CPU.

 x = torch.FloatTensor(1024, 1024).uniform_()

Память видеокарты при этом пуста.

 0MiB /  4036MiB

Одним вызовом мы можем переместить тензор на GPU.

 x = x.cuda()

При этом nvidia-smi покажет, что процесс python занял некоторое количество видеопамяти.

 205MiB /  4036MiB

Свойство x.is_cuda поможет понять где сейчас находится тензор x.

>>>  x.is_cuda True

На самом деле x.cuda() возвращает копию тензора, а не перемещает его.

Когда исчезнут все ссылки на тензор, находящийся в видеопамяти, PyTorch не удалит его моментально. Вместо этого при следующем выделении он либо переиспользует этот участок видеопамяти, либо очистит её.

Если у вас несколько видеокарт, функция x.cuda(device=None) с радостью примет в качестве опционального аргумента номер видеокарты, куда стоит положить тензор, а функция x.get_device() покажет на каком устройстве тензор x находится. Функция x.cpu() скопирует тензор из видеокарты "на процессор".

Естественно, мы не можем производить никакие операции с тензорами, находящимеся на разных устройствах.

Вот, например, как можно перемножить два тензора на видеокарте и вернуть результат обратно в оперативную память:

>>>  import torch >>> a = torch.FloatTensor(10000, 10000).uniform_() >>> b = torch.FloatTensor(10000, 10000).uniform_() >>> c = a.cuda().mul_(b.cuda()).cpu()

И всё это доступно прямо из интерпретатора! Представьте аналогичный код на TensorFlow, где вам придётся создать граф, сессию, скомпилировать граф, инициализировать переменные и запустить граф на сессии. С помощью PyTorch я могу даже отсортировать тензор на видеокарте одной строчкой кода!

Тензоры можно не только копировать на видеокарту, но и создавать их прямо на ней. Для этого используется модуль torch.cuda.

В torch.cuda нет сокращения Tensor = FloatTensor.

Контекстный менеджер torch.cuda.device(device) позволяет создавать все определённые внутри него тензоры на указанной видеокарте. Результаты операций над тензорами с других устройств останутся там, где и должны быть. Переданное в x.cuda(device=None) значение приоритетнее, чем то, которое диктует контекстный менеджер.

 x = torch.cuda.FloatTensor(1) # x.get_device() == 0 y = torch.FloatTensor(1).cuda() # y.get_device() == 0  with torch.cuda.device(1):     a = torch.cuda.FloatTensor(1)     # a.get_device() == 1      b = torch.FloatTensor(1).cuda()     # a.get_device() == b.get_device() == 1      c = a + b     # c.get_device() == 1      z = x + y     # z.get_device() == 0      d = torch.FloatTensor(1).cuda(2)     # d.get_device() == 2

Функция x.pin_memory(), доступная только для тензоров на CPU, копирует тензор в page-locked область памяти. Особенность её в том, что данные из неё могут быть очень быстро скопированы на GPU без участия процессора. Метод x.is_pinned() покажет текущий статус тензора. После того, как тензор окажется в page-locked памяти, мы можем передать именованный параметр async=True функции x.cuda(device=None, async=False), чтобы попросить её загружать тензор на видеокарту асинхронно. Таким образом, ваш код может не ждать завершения копирования и сделать за это время что-нибудь полезное.

Параметр async не имеет эффекта, если x.is_pinned() == False. Ошибки это тоже не вызовет.

Как видите, адаптация произвольного вашего кода для вычислений на видеокарте требует лишь копирования всех тензоров в видеопамять. Большинству операций без разницы, где находятся ваши тензоры, если они находятся на одном устройстве.

Автоматическое дифференцирование

Механизм автоматического дифференцирования, заключённый в модуле torch.autograd, является хоть и не главным, но, без сомнения, важнейшим компонентом библиотеки, без которого та потеряла бы всякий смысл.

Вычисление градиента функции в заданной точке — центральная операция методов оптимизации, на которых, в свою очередь, держится всё глубокое обучение. Обучение здесь — синоним оптимизации. Существует три основных способа вычислить градиент функции в точке:

1. Численно методом конечных разностей;
2. Символьно;
3. Использовать технику автоматического дифференцирования.

Первым методом пользуются лишь для проверки результатов из-за его низкой точности. Символьное вычисление производной эквивалентно тому, что вы делаете вручную, используя бумагу и карандаш, и заключается в применении списка правил к дереву символов. Про автоматическое же дифференцирование я расскажу в следующих параграфах. Библиотеки вроде Caffe и CNTK используют заранее предпосчитанную производную функции в символьном виде. Theano и TensorFlow используют комбинацию методов 2 и 3.

Автоматическое дифференцирование (AD) — достаточно простая и весьма очевидная техника вычисления градиента функции. Если вы, не используя интернет, попытаетесь решить задачу дифференцирования функции в заданной точке, вы совершенно точно придёте к AD.

Вот как AD работает. Любую из интересующих нас функций можно выразить как композицию некоторых элементарных функций, производные которых нам известны. Затем, используя правило дифференцирования сложной функции, мы можем подниматься всё выше и выше, пока не придём к искомой производной. Например, рассмотрим фукнцию двух переменных

Переобозначим

Каждая из получившихся функций является элементарной функцией — мы можем с лёгкостью вычислить её производную.

Допустим, нас инетересует

По правилу дифференцирования сложной функции можем записать

Все компоненты этого уравнения — производные элементарных функций и начальные значения — нам известны. Осталось лишь подставить их и вычислить результат. Однако подстановку мы будем совершать не в произвольном порядке, а начнём с начала — самых вложенных элементов.

Вот так за один проход мы можем вычислить производную функции в заданной точке. И необходимо для этого ровно такое же количество операций, как и для вычисления самой функции. Обратите внимание, что икс со звёздочкой — не символ, а некоторое числовое значение. Поэтому на каждом шаге рассмотренного алгоритма мы сохраняем не символьное выражение, а одно единственное число — текущее значение производной.

Чтобы лучше понять AD, мы можем реализовать простейший его вариант всего в 20 строчек кода на чистом Python! Будем вычислять значение функции и её производную в одной и той же точке одновременно. Первым делом запомним значение переменной в точке и её производную.

 class Varaible:     def __init__(self, value, derivative):         self.value = value         self.derivative = derivative

При сложении двух переменных мы сконструируем новую переменную, значение которой будет равняться сумме исходных переменных, а производная будет вычисляться по правилу вычисления производной суммы двух функций.

     def __add__(self, other):         return Varaible(             self.value + other.value,             self.derivative + other.derivative         )

Аналогично для умножения и возведения в степень

     def __mul__(self, other):         return Varaible(             self.value * other.value,             self.derivative * other.value + self.value * other.derivative         )      def __pow__(self, other):         return Varaible(             self.value ** other,             other * self.value ** (other - 1)         )

Теперь мы с лёгкостью можем одновременно вычислить и значение нашей функции и её частную производную по переменной x1 за один проход.

 def f(x1, x2):     vx1 = Varaible(x1, 1)     vx2 = Varaible(x2, 0)     vf = vx1 * vx2 + vx1 ** 2     return vf.value, vf.derivative  print(f(2, 3)) # (10, 7)

Ровно таким же поведением обладает класс Variable из модуля torch.autograd. Конечно, в отличии от нашей наивной реализации, он хорошо оптимизирован, поддерживает тензоры PyTorch и все возможные с ними дифференцируемые операции. К тому же, он вычисляет производную не по одному аргументу за раз, а по всем сразу. Давайте рассмотрим пример.

>>>  from torch.autograd import Variable  >>> x = torch.FloatTensor(3, 1).uniform_() >>> w = torch.FloatTensor(3, 3).uniform_()  >>> b = torch.FloatTensor(3, 1).uniform_()  >>> x = Variable(x, requires_grad=True) >>> w = Variable(w) >>> b = Variable(b)  >>> y = w.mv(x).add_(b) >>> y Variable containing:  0.7737  0.6839  1.1542 [torch.FloatTensor of size 3]  >>> loss = y.sum() >>> loss Variable containing:  2.6118 [torch.FloatTensor of size 1]  >>> loss.backward() >>> x.grad Variable containing:  0.2743  1.0872  1.6053 [torch.FloatTensor of size 3]

И снова нам никак не нужно изменять наш код для вычислений: достаточно лишь обернуть тензоры в Variable и он сам позабитится о сохранении всех методов и свойств, а также добавит парочку новых. x.backward() выполнит обратный проход и посчитает производную по всем переменным, при создании которых мы указали requires_grad=True. Производная при этом запишется в свойство x.grad. Получить же свой тензор обратно мы можем используя свойство x.data.

В операциях нельзя смешивать обычные тензоры и тензоры, обёрнутые в Variable.

Свойство x.requires_grad покажет, нуждается ли узел графа в вычислении градиента. Правило такое: если хоть у одного дочернего узла это свойство установлено, оно будет установлено и у родителя.

Что стоит обсудить отдельно, так это inplace операции. Далеко не все такие операции, доступные для тензора, доступны для Variable, так как исходное значение тензора может быть необходимо для вычисления производной. Общее правило: пока у вас нет серьёзных ограничений по памяти, лучше всегда использовать immutable операции. В противном случае придётся рассматривать каждую отдельно взятую операцию на предмет возможности её замены mutable версией. Волноваться здесь не стоит: PyTorch никогда не разрешит вам сделать что-то, что молча приведёт к неправильному результату вычислений.

Пример

В качестве примера мы не будем обучать однослойный перцептрон и даже не будем строить FaceResNet-1337. С этими задачами PyTorch, как и остальные фреймворки, справляется играючи, а массу подобных примеров легко найти в сети. Мы посмотрим на задачу, от которой остальные фреймворки в ужасе разбегутся.

Допустим, вы прочитали статью Deep Function Machines: Generalized Neural Networks for Topological Layer Expression и решили попробовать реализовать её на практике. Статья обобщает слой нейронной сети как отображение между произвольными Хаусдорфовыми пространствами. Таким образом мы можем построить слой нейронной сети с непрерывным ядром, отображающий одно функциональное пространство в другое. Автор доказывает теорему, о том, что произвольному такому слою соответствует дискретный слой стандартной нейронной сети, причём единственный. Отношение это определяется следующим образом:

Без вывода и доказательства результат кажется достаточно простым. w — непрерывное параметризованное ядро, W — дискретное ядро, которое мы строим. Осталось лишь для каждого прохода вычислить W, применить его к каким-нибудь данным, посчитать производные, распространить ошибку через интеграл и обновить параметры w. Звучит легко? Для PyTorch — да. В качестве ядра используем волновое ядро из статьи.

 import numpy as np import torch from torch.autograd import Variable  def kernel(u, v, s, w, p):     uv = Variable(torch.FloatTensor([u, v]))      return s[0] + w.mv(uv).sub_(p).cos().dot(s[1:])

Быстро реализуем простейшую схему интегрирования.

 def integrate(fun, a, b, N=100):     res = 0     h = (b - a) / N      for i in np.linspace(a, b, N):         res += fun(a + i) * h      return res

Теперь так же быстро накидаем всё остальное.

 def V(v, n, s, w, p):     fun = lambda u: kernel(u, v, s, w, p).mul_(u - n)     return integrate(fun, n, n+1)  def Q(v, n, s, w, p):     fun = lambda u: kernel(u, v, s, w, p)     return integrate(fun, n, n+1)  def W(N, s, w, p):     Qp = lambda v, n: Q(v, n, s, w, p)     Vp = lambda v, n: V(v, n, s, w, p)      W = [None] * N     W[0] = torch.cat([Qp(v, 1) - Vp(v, 1) for v in range(1, N + 1)])     for j in range(2, N):         W[j-1] = torch.cat([Qp(v, j) - Vp(v, j) + Vp(v, j - 1) for v in range(1, N + 1)])     W[N-1] = torch.cat([ Vp(v, N-1) for v in range(1, N + 1)])      W = torch.cat(W)      return W.view(N, N).t()

Инициализируем наши веса.

 s = Variable(torch.FloatTensor([1e-5, 1, 1]), requires_grad=True) w = Variable(torch.FloatTensor(2, 2).uniform_(-1e-5, 1e-5), requires_grad=True) p = Variable(torch.FloatTensor(2).uniform_(-1e-5, 1e-5), requires_grad=True)

Подготовим данные.

 data_x_t = torch.FloatTensor(100, 3).uniform_() data_y_t = data_x_t.mm(torch.FloatTensor([[1, 2, 3]]).t_()).view(-1)

И обучим наш прототип.

 alpha = -1e-3 for i in range(1000):     data_x, data_y = Variable(data_x_t), Variable(data_y_t)      Wc = W(3, s, w, p)     y = data_x.mm(Wc).sum(1)     loss = data_y.sub(y).pow(2).mean()      print(loss.data[0])      loss.backward()     s.data.add_(s.grad.data.mul(alpha))     s.grad.data.zero_()      w.data.add_(w.grad.data.mul(alpha))     w.grad.data.zero_()      p.data.add_(p.grad.data.mul(alpha))     p.grad.data.zero_()

Запустим и увидим в терминале стройную колонну убывающих значений. Ниже показано как ядро меняется в процессе обучения.

Я даже не вспотел. Я разбирался с 3d графиками в matplotlib дольше, чем писал этот код. Да, он не идеален, но это работающий прототип, созданный за 15 минут. Считать вручную все эти производные нереально. TensorFlow… Я не представляю, как реализовать это на TensorFlow. PyTorch же наплевал на сложность и безумность вашей идеи. Если функция дифференцируема, PyTorch её дифференцирует. Если вам нужно перемножить тензоры на видеокарте, PyTorch не заставит вас определять граф, он позволит вам просто перемножить тензоры на видеокарте.

Рассмотрим код обучения поближе.

 data_x, data_y = Variable(data_x_t), Variable(data_y_t)

Этот код оборачивает наши тензоры в переменные, чтобы все дальнейшие вычисления строили за собой граф. Каждый раз это необходимо делать из-за того что наш граф динамический и, следовательно, одноразовый: совершить обратный проход по нему можно лишь единожды.

 loss.backward()

Этот вызов, как вам уже должно быть известно, считает обратный проход по графу.

 s.data.add_(s.grad.data.mul(alpha))

Здесь мы берём тензор из посчитанного градиента (переменной), домножаем его на некоторое маленькое по модулю отрицательное число и прибавляем к тензору исходных весов на месте. Таким образом совершается один шаг градиентного спуска.

 s.grad.data.zero_()

Вызов backward() не обнуляет градиент, поэтому нужно сделать это вручную.

Естественно, вам не придётся каждый раз вручную писать весь этот код: для стандартных задач в PyTorch предусмотрены все те же высокоуровневые абстракции, что и, например, в Keras.

Заключение

В данной статье мы рассмотрели основы PyTorch: тензорные вычисления, cuda вычисления и автоматическое дифференцирование. Тепреь вы с лёгкостью можете взять PyTorch и начать заниматься глубоким обучением с его помощью.

Читателю может показаться, что PyTorch слишком низкоуровневый. Кажется, что для продуктивной работы над всем этим ещё предстоит написать удобную обёртку. С одной стороны это так: никто не запрещает вам написать поверх PyTorch ту обёртку, которая удобна лично вам. Вы можете написать её в модульном стиле, как в Caffe, а можете описать свой собственный декларативный DSL как в TensorFlow. PyTorch низкоуровневый настолько, насколько это только возможно и позволяет вам создавать поверх него те инструменты, с которыми будет максимально удобно работать лично вам.

С другой стороны, существуют официальные реализации таких высокоуровневых обёрток, заключённые в модулях torch.nn и torch.optim. Модуль torch.utils.data позволяет крайне удобно асинхронно работать с данными. Отдельный пакет torchvision содержит всё необходимое для быстрого старта работы с изображениями. Обо всём этом поговорим в следующей статье.

PyTorch великолепен. Он предоставляет вам различные уровни абстракции и позволяет с лёгкостью реализовывать свои. Он не загоняет вас в рамки какой-то одной парадигмы. Он быстрый, эффективный и распределённый. Попробуйте его и он вам непременно понравится.

Спасибо за прочтение! Ставьте лайки, подписывайтесь на профиль, оставляйте комментарии, не тратьте время на борьбу с инструментами. Дополнения приветствуются.