Машинное обучение: от Ирисов до Телекома

Мобильные операторы, предоставляя разнообразные сервисы, накапливают огромное количество статистических данных. Я представляю отдел, реализующий систему управления трафиком абонентов, которая в процессе эксплуатации у оператора генерирует сотни гигабайт статистической информации в сутки. Меня заинтересовал вопрос: как в этих Больших Данных (Big Data) выявить максимум полезной информации? Не зря ведь одна из V в определении Big Data — это дополнительный доход.

Я взялся за эту задачу, не являясь специалистом в исследовании данных. Сразу возникла масса вопросов: какие технические средства использовать для анализа? На каком уровне достаточно знать математику, статистику? Какие методы машинного обучения надо знать и насколько глубоко? А может лучше для начала освоить специализированный язык для исследования данных R или Python?

Как показал мой опыт, для начального уровня исследования данных нужно совсем не много. Но мне для быстрого погружения не хватало простого примера, на котором наглядно был бы показан полный алгоритм исследования данных. В этой статье на примере Ирисов Фишера мы пройдем весь путь начального обучения, а далее применим полученное понимание к реальным данным оператора связи. Читатели, уже знакомые с исследованием данных, могут сразу переходить к главе, посвященной Телекому.

Термины

Для начала давайте разберемся с предметом изучения. Сейчас термины Искусственный Интеллект, Машинное Обучение, Глубокое Машинное Обучение зачастую используются как синонимы, но на самом деле существует вполне определенная иерархия: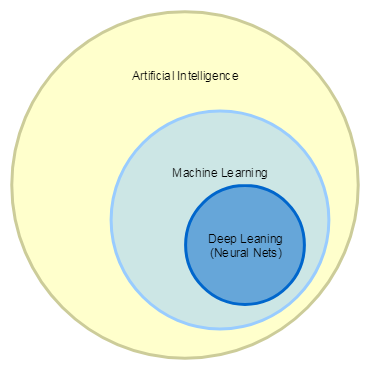

• К Искусственному Интеллекту относятся все задачи, в которых машины выполняют интеллектуальные задачи, такие как игра в шашки или шахматы, помощники, способные распознавать речь и давать ответы на вопросы, разнообразные роботы.
• Машинное Обучение – более узкое понятие и относится к классу задач, для решения которых компьютер обучают выполнять определенные действия, имея заранее известные правильные ответы, например, классификация объектов по набору признаков или рекомендация музыки и фильмов.
• Под Глубоким Обучением подразумевают задачи, которые решаются с помощью нейронных сетей и Больших Данных, такие как распознавание образов или перевод текста.

В статье мы будем говорить о Машинном Обучении. В нем выделяют два способа обучения:

• с учителем
• без учителя

С учителем – это когда у нас есть данные с правильными ответами. Тогда алгоритм можно обучить на этом наборе данных, и далее применять его для предсказания. К таким алгоритмам относится классификация и регрессия. Классификация — это отнесение объектов к определенному классу по набору признаков. Например, распознавание номеров машин, или в медицине диагностика заболеваний, или кредитный скоринг в банковской сфере. Регрессия – это предсказание вещественной переменной, например, цен на акции.

Без учителя (самообучение) – это поиск скрытых закономерностей в данных. К таким алгоритмам относится кластеризация. Например, все крупные торговые сети ищут закономерности в покупках своих клиентов и пытаются работать с целевыми группами покупателей, а не с общей массой.

Регрессия, классификация и кластеризация являются основными алгоритмами исследования данных, поэтому их и будем рассматривать.

Исследование данных

Алгоритм исследования данных состоит из определенной последовательности шагов. В зависимости от задачи и имеющихся данных набор шагов может меняться, но общее направление всегда определенное:

• Сбор и очистка данных. Как показывает практика, этот этап может занимать до 90% времени всего анализа данных;
• Визуальный анализ данных, их распределение, статистики;
• Анализ зависимости (корреляции) между переменными (признаками);
• Отбор и определение признаков, которые будут использоваться для построения моделей;
• Разделение на данные для обучения модели и тестовые;
• Построение моделей на данных для обучения / оценка результата на тестовых данных;
• Интерпретация полученной модели, визуализация результатов.

С алгоритмом разобрались, а какие средства использовать для анализа? Существует масса средств, от Excel до специализированных средств, например, MathLab. Мы возьмем Python cо специализированными библиотеками. Не надо опасаться сложностей, тут все просто:

• Скачиваем Python и все математические пакеты в одном дистрибутиве, который называется Анаконда
• Установка под Linux проблем не вызовет: bash Anaconda2-4.4.0-Linux-x86_64.sh

• Запускаем: jupyter notebook

• При этом автоматически открывается браузер:

• Проверяем, что приложение работает: print «HelloWorld!»

• Нажимаем Ctrl+Enter, смотрим, что все ok.

Для самостоятельного изучения работы в IPython Notebook в интернете есть масса информации, например, простое введение: Обзор Ipython Notebook 2.0.

А мы начинаем наше исследование!

Сбор и очистка данных

В примере с Ирисами для нас все данные собрали и заполнили. Просто загружаем их и смотрим:

#Импортируем нужные библиотеки: import numpy as np import pandas as pd from sklearn import datasets from sklearn import linear_model from sklearn.cluster import KMeans from sklearn import cross_validation from sklearn import metrics  from pandas import DataFrame %pylab inline

Далее:

# Загружаем набор данных Ирисы: iris = datasets.load_iris() # Смотрим на названия переменных print iris.feature_names # Смотрим на данные, выводим 10 первых строк:  print iris.data[:10] # Смотрим на целевую переменную: print iris.target_names print iris.target

Видим, что набор данных состоит из длины/ширины двух типов лепестков Ириса: sepal и petal. Не спрашивайте меня, где они находятся у Ириса). Целевая переменная — это сорт Ириса: 0 — Setosa, 1 — Versicolor, 2 — Virginica. Соответственно, наша задача — по имеющимся данным попробовать найти зависимости между размерами лепестков и сортами Ирисов.

Для удобства манипулирования данными делаем из них DataFrame:

iris_frame = DataFrame(iris.data) # Делаем имена колонок такие же, как имена переменных: iris_frame.columns = iris.feature_names # Добавляем столбец с целевой переменной:  iris_frame['target'] = iris.target # Для наглядности добавляем столбец с сортами:  iris_frame['name'] = iris_frame.target.apply(lambda x : iris.target_names[x]) # Смотрим, что получилось: iris_frame

Вроде получилось, то что хотели:

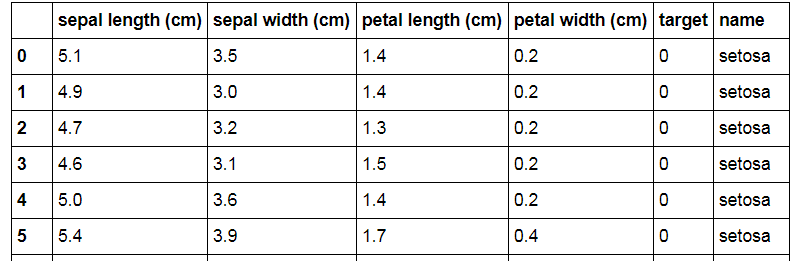
Описательные статистики

# Строим гистограммы по каждому признаку:  pyplot.figure(figsize(20, 24)) plot_number = 0 for feature_name in iris['feature_names']: for target_name in iris['target_names']:    plot_number += 1    pyplot.subplot(4, 3, plot_number)    pyplot.hist(iris_frame[iris_frame.name == target_name][feature_name])    pyplot.title(target_name)    pyplot.xlabel('cm')    pyplot.ylabel(feature_name[:-4])

Посмотрев на такие гистограммы, опытный исследователь может сразу делать первые выводы. Я вижу только, что распределение у некоторых переменных похоже на нормальное. Попробуем сделать более наглядно. Строим таблицу с зависимостями между признаками и раскрашиваем точки в зависимости от сортов Ирисов:

import seaborn as sns sns.pairplot(iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)','name']], hue = 'name')

Тут уже даже неискушенному исследователю видно, что «petal width (cm)» и «petal length (cm)» имеют сильную зависимость — точки вытянуты вдоль одной линии. И в принципе по этим же признакам можно строить классификацию, т.к. точки по цвету сгруппированы достаточно компактно. А вот, например, с помощью переменных «sepal width (cm)» и «sepal length (cm)» качественную классификацию не построить, т.к. точки, относящиеся к сортам Versicolor и Virginica, перемешаны между собой.

Зависимость между переменными

Теперь посмотрим на математические значения зависимостей:

iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']].corr()

В более наглядном виде построим тепловую карту зависимости признаков:

import seaborn as sns corr = iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']].corr() mask = np.zeros_like(corr) mask[np.triu_indices_from(mask)] = True with sns.axes_style("white"): ax = sns.heatmap(corr, mask=mask, square=True, cbar=False, annot=True, linewidths=.5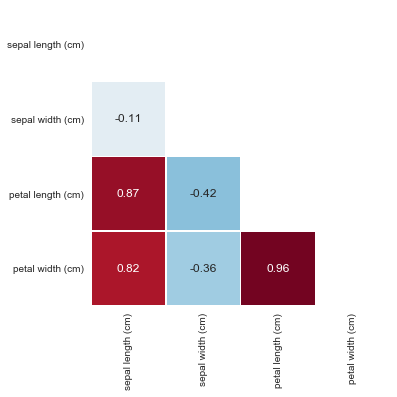

Значения коэффициента корреляции интерпретируются следующим образом:

• До 0,2 — очень слабая корреляция
• До 0,5 — слабая
• До 0,7 — средняя
• До 0,9 — высокая
• Больше 0,9 — очень высокая

Действительно видим, что между переменными «petal length (cm)» и «petal width (cm)» выявлена очень сильная зависимость 0.96.

Отбираем и создаем признаки

В первом приближении можно просто включить все переменные в модель и посмотреть, что будет. Далее можно будет подумать, какие признаки убрать, а какие создать.

Данные для обучения и тестовые данные

Разделяем данные на данные для обучения и тестовые данные. Обычно выборку разделяют на обучающую и тестовую в процентном соотношении 66/33, 70/30 или 80/20. Возможны и другие разбиения в зависимости от данных. В нашем примере на тестовые данные отводим 30% от всей выборки (параметр test_size = 0.3):

train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']], iris_frame['target'], test_size = 0.3, random_state = 0) # визуально проверяем, что получившееся разбиение соответствует нашим ожиданиям: print train_data print test_data print train_labels print test_labels

Цикл построения моделей – оценка результата

Переходим к самому интересному.

Линейная регрессия – LinearRegression

Как наглядно представить линейную регрессию? Если смотреть на зависимость между двумя переменными, то это проведение линии так, чтобы расстояния от линии до точек были в сумме минимальные. Самый распространенный способ оптимизации – это минимизация среднеквадратичной ошибки по алгоритму градиентного спуска. Объяснение градиентного спуска есть много где, например тут в разделе “Что такое градиентный спуск?”. Но можно не читать и воспринимать линейную регрессию как абстрактный алгоритм нахождения линии, которая наиболее точно повторяет направление распределения объектов. Строим модель, используя переменные, которые, как мы поняли ранее, имеют сильную зависимость — это «petal length (cm)» и «petal width (cm)»:

from scipy import polyval, stats fit_output = stats.linregress(iris_frame[['petal length (cm)','petal width (cm)']]) slope, intercept, r_value, p_value, slope_std_error = fit_output print(slope, intercept, r_value, p_value, slope_std_error)

Смотрим на метрики качества модели:

(0.41641913228540123, -0.3665140452167277, 0.96275709705096657, 5.7766609884916033e-86, 0.009612539319328553)
Из наиболее интересного — это коэффициент корреляции между переменными r_value со значением 0.96275709705096657. Его мы уже видели ранее, а здесь еще раз убедились в его существовании. Рисуем график с точками и линией регрессии:

import matplotlib.pyplot as plt plt.plot(iris_frame[['petal length (cm)']], iris_frame[['petal width (cm)']],'o', label='Data') plt.plot(iris_frame[['petal length (cm)']], intercept + slope*iris_frame[['petal length (cm)']], 'r', linewidth=3, label='Linear regression line') plt.ylabel('petal width (cm)') plt.xlabel('petal length (cm)') plt.legend() plt.show()

Видим, что, действительно, найденная линия регрессии хорошо повторяет направление распределения точек. Теперь, если у нас будет в наличии, например, длина листочка pental, мы сможем с большой точностью определить, какая у него ширина!

Классификация

Как интуитивно представить классификацию? Если смотреть на задачу разделения на два класса объектов, которые имеют два признака (например, нужно разделить яблоки и бананы, если известны их размеры), то классификация сводится к проведению линии на плоскости, которая делит объекты на два класса. Если надо разделить на большее число классов, то проводится несколько линий. Если смотреть на объекты с тремя переменными, то представляется трехмерное пространство и задача проведения плоскостей. Если переменных N, то нужно просто вообразить гиперплоскость в N-мерном пространстве). Итак, берем самый известный алгоритм классификации: стохастический градиентный спуск (Stochastic Gradient Descent). С градиентным спуском мы уже встречались в линейной регрессии, а стохастический говорит о том, что для быстроты работы используется не вся выборка, а случайные данные.

train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']], iris_frame[['target']], test_size = 0.3, random_state = 0) model = linear_model.SGDClassifier(alpha=0.001, n_iter=100, random_state = 0) model.fit(train_data, train_labels) model_predictions = model.predict(test_data) print metrics.accuracy_score(test_labels, model_predictions) print metrics.classification_report(test_labels, model_predictions)

Смотрим на метрики качества модели:

На самом деле, оценить модель можно, не особо разбираясь в сути значений метрик: если accuracy, precision и recall больше 0.85, то это хорошая модель, если больше 0.95, то отличная.

Если кратко, то используемые в примере метрики отражают следующее:

• accuracy — это главная метрика, которая показывает долю правильных ответов модели. Ее значение равно отношению числа правильных ответов, которые дала модель, к числу всех объектов. Но она не полностью отражает качество модели. Поэтому вводятся precision и recall.

Эти метрики даны как в разрезе качества распознавания каждого класса (сорта ириса), так и суммарные значения. Смотрим на суммарные значения:

• precision (точность) — эта метрика показывает, насколько мы можем доверять модели, другими словами, какое у нас количество «ложных срабатываний». Значение метрики равно отношению числа ответов, которые модель считает правильными, и они действительно были правильными (это число обозначается «true positives») к сумме «true positives» и числа объектов которые модель посчитала правильными, а на самом деле они были неправильные (это число обозначается «false positives»). В виде формулы: precision = «true positives» / («true positives» + «false positives»)
• recall (полнота) — эта метрика показывает насколько модель может вообще обнаруживать правильные ответы, другими словами, какое у нас количество «ложных пропусков». Ее численное значение равно отношению ответов, которые модель считает правильными, и они действительно были правильными к числу всех правильных ответов в выборке. В виде формулы: recall = «true positives» / «all positives»
• f1-score (f-мера) — это объединение precision и recall
• support — просто число найденных объектов в классе

Есть еще важные метрики модели: PR-AUC и ROC-AUC, с ними можно ознакомиться, например, тут: Метрики в задачах машинного обучения.

Таким образом, видим, что значения метрик на нашем примере очень хорошие. Посмотрим на график. Для наглядности выборку рисуем в двух координатах и раскрашиваем по классам.

Сначала отобразим тестовую выборку, как она есть:

Потом, как ее предсказала наша модель. Видим, что точки на границе (которые я обвел красным) были классифицированы неправильно:

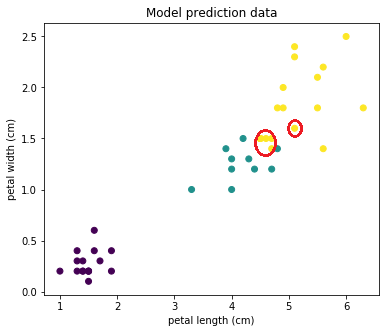
Но при этом большинство объектов предсказано правильно!

Cross-Validation

Как-то уж очень подозрительно хороший результат… Что может быть не так? Например, мы случайно хорошо разбили данные на обучающую и тестовую выборку. Чтобы убрать эту случайность применяют так называемую кросс-валидацию. Это когда данные разбиваются несколько раз на обучающую и тестовую выборку, и результат работы алгоритма усредняется. Проверим работу алгоритма на 10 случайных выборках:

train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']], iris_frame['target'], test_size = 0.3) model = linear_model.SGDClassifier(alpha=0.001, n_iter=100, random_state = 0) scores = cross_validation.cross_val_score(model, train_data, train_labels, cv=10) print scores.mean()

Смотрим на результат. Он ожидаемо ухудшился: 0.860909090909

Подбор оптимальных параметров алгоритма

Что еще можно сделать для оптимизации алгоритма? Можно попытаться подобрать параметры самого алгоритма. Видим, что в алгоритм передаются alpha=0.001, n_iter=100. Давайте найдем для них оптимальные значения.

from sklearn import grid_search train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']], iris_frame['target'], test_size = 0.3) parameters_grid = { 'n_iter' : range(5,100), 'alpha' : np.linspace(0.0001, 0.001, num = 10), } classifier = linear_model.SGDClassifier(random_state = 0) cv = cross_validation.StratifiedShuffleSplit(train_labels, n_iter = 10, test_size = 0.3, random_state = 0) grid_cv = grid_search.GridSearchCV(classifier, parameters_grid, scoring = 'accuracy', cv = cv)grid_cv.fit(train_data, train_labels) print grid_cv.best_estimator_

На выходе получаем модель с оптимальными параметрами:

SGDClassifier(alpha=0.00089999999999999998, average=False, class_weight=None,
epsilon=0.1, eta0=0.0, fit_intercept=True, l1_ratio=0.15,
learning_rate='optimal', loss='hinge', n_iter=96, n_jobs=1,
penalty='l2', power_t=0.5, random_state=0, shuffle=True, verbose=0,
warm_start=False)

Видим, что в ней alpha=0.0009, n_iter=96. Подставляем эти значения в модель:

train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']], iris_frame['target'], test_size = 0.3) model = linear_model.SGDClassifier(alpha=0.0009, n_iter=96, random_state = 0) scores = cross_validation.cross_val_score(model, train_data, train_labels, cv=10) print scores.mean()

Смотрим, стало немного лучше: 0.915505050505

Отбираем и создаем признаки

Пришло время поэкспериментировать с признаками. Давайте уберем из модели менее значимые признаки, а именно «sepal length (cm)» и «sepal width (cm)». Загоняем в модель:

train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(iris_frame[['petal length (cm)','petal width (cm)']], iris_frame['target'], test_size = 0.3) model = linear_model.SGDClassifier(alpha=0.0009, n_iter=96, random_state = 0) scores = cross_validation.cross_val_score(model, train_data, train_labels, cv=10) print scores.mean()

Смотрим, стало еще немного лучше: 0.937727272727
Для иллюстрации подхода, давайте сделаем новый признак: площадь листка petal и посмотрим, что получится.

iris_frame['petal_area'] = 0.0 for k in range(0,150): iris_frame['petal_area'][k] = iris_frame['petal length (cm)'][k] * iris_frame['petal width (cm)'][k] 

Подставляем в модель:

train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(iris_frame[['petal_area']], iris_frame['target'], test_size = 0.3) model = linear_model.SGDClassifier(alpha=0.0009, n_iter=96, random_state = 0) scores = cross_validation.cross_val_score(model, train_data, train_labels, cv=10) print scores.mean()

Забавно, но в нашем примере получается, что площадь лепестка petal (вернее, даже не площадь, т.к. лепестки не прямоугольники, а «произведение длины на ширину») наиболее точно предсказывает сорт Ириса: 0.942373737374

Наверно, это можно объяснить тем, что переменные 'petal length (cm)' и 'petal width (cm)', и так неплохо разделяет Ирисы на классы, а их произведение еще «растягивает» классы вдоль прямой:

Мы познакомились с основными способами оптимизации моделей, теперь рассмотрим алгоритм кластеризации — пример машинного обучения без учителя.

Кластеризация — K-means

Суть кластеризации крайне проста — необходимо разделить имеющиеся объекты на группы, так чтобы в группы входили похожие объекты. У нас теперь нет правильных ответов для обучения модели, поэтому алгоритм должен сам группировать объекты по «близости» расположения объектов друг к другу. Для примера, рассмотрим самый известный алгоритм K-средних. Он не зря называется K-средних, т.к. метод основан на нахождении K центров кластеров так, чтобы среднее расстояния от них до объектов, которые им принадлежат были минимальные. Сначала алгоритм определяет K произвольных центров, далее все объекты распределяются по близости к этим центрам. Получили K кластеров объектов. Далее в этих кластерах заново вычисляются центры по среднему расстоянию до объектов, и объекты снова перераспределяются. Алгоритм работает до тех пор, пока центры кластеров не перестанут сдвигаться на какую-то определенную дельту.

train_data, test_data, train_labels, test_labels = cross_validation.train_test_split(iris_frame[['sepal length (cm)','sepal width (cm)','petal length (cm)','petal width (cm)']], iris_frame[['target']], test_size = 0.3) model = KMeans(n_clusters=3) model.fit(train_data) model_predictions = model.predict(test_data) print metrics.accuracy_score(test_labels, model_predictions) print metrics.classification_report(test_labels, model_predictions)

Смотрим на результаты:

Видим, что даже с параметрами по умолчанию получается очень неплохо: accuracy, precision и recall больше 0.9. Убеждаемся на картинках. Видим достойный, но не везде точный результат:


У алгоритма есть недостаток — для его работы нужно задавать число кластеров, которое мы хотим найти. И если оно будет неадекватное, то результаты работы алгоритма будут бесполезны. Посмотрим, что будет, если задать число кластеров, например, 5:

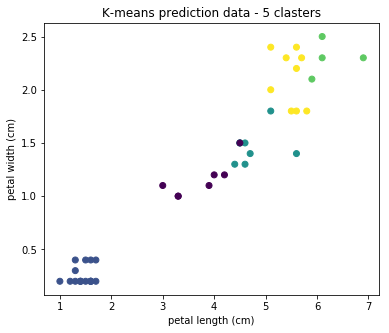
Видим, что на практике результат не применим. Существуют алгоритмы определения оптимального числа кластеров, но в этой статье мы не будем на них останавливаться.

Заключение по исследованию Ирисов

Итак, на примере Ирисов мы рассмотрели три основных метода машинного обучения: регрессию, классификацию и кластеризацию. Провели оптимизацию алгоритмов и визуализацию результатов. Получили очень хорошие результаты, но это и было ожидаемо на специально подготовленном наборе данных. Полный Python Notebook можно найти на Github. Переходим к Телекому.

Телеком

В Телекоме есть задачи, которые с помощью анализа данных решают и в других сферах (банки, страхование, ретейл):

• Предсказание оттока абонентов (Churn Prevention);
• Обнаружение мошенничества (Fraud Prevention);
• Выявление похожих абонентов (Сегментация абонентской базы);
• Перекрестные продажи (Cross-Sale) и поднятие суммы продажи (Up-Sale);
• Выявление абонентов, сильно влияющих на свое окружение (Альфа-абоненты).

Кроме того, имеются и специфичные задачи:

• Предсказание потребления ресурсов сети абонентами: объём трафика, число звонков, SMS;
• Исследование перемещений абонентов с целью оптимизации сети.

Откуда оператор связи может получить данные для анализа? Из разнообразных информационных систем и оборудования, которое участвует в предоставлении услуг абонентам:

• В биллинговой системе хранятся данные по платежам и расходам абонентов, тарифы, персональные данные;
• Из оборудования DPI извлекаются данные о том, какие сайты посещал абонент;
• C базовых станций можно получить геоданные c местонахождением абонента;
• Оборудование обслуживания генерирует данные о потреблении абонентом услуг связи.

Моей целью было определить, какие задачи можно попробовать решить с помощью данных, которые генерирует система по управлению трафиком абонентов. Для того чтобы биллинговая система правильно тарифицировала трафик абонента, ей необходимо знать: кто / где / когда / какого типа и объема трафик потребил. Эта информация поступает с оборудования в виде, так называемых, CDR (Call Data Record) файлов. В эти файлы в формате csv записываются идентификаторы абонента IMSI и MSISDN, местоположение c точностью до базовой станции CELL ID, идентификатор оборудования абонента IMEI, временная метка сессии и информация о потребленной услуге.

Для соблюдения конфиденциальности все данные для исследования были обезличены и заменены на случайные значения с соблюдением формата. Посмотрим на данные:

Какие алгоритмы машинного обучения можно применить к этим данным? Можно, например, агрегировать потребление трафика разного типа по абонентам за определенный период и провести кластеризацию. Должна получиться примерно такая картинка:

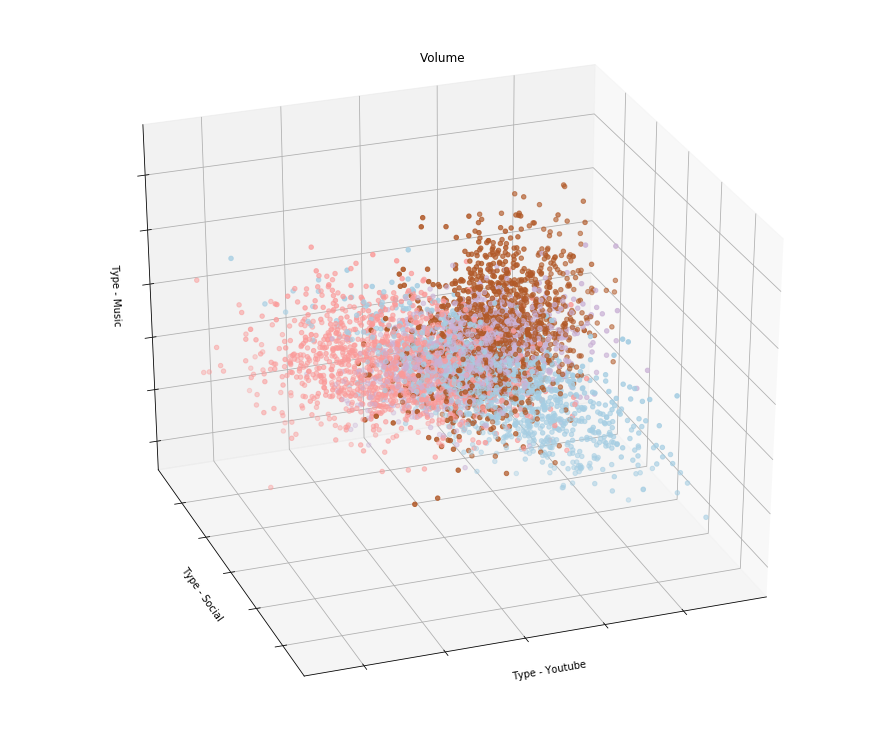
Т.е. если, например, результат кластеризации показал, что абоненты разделились на группы, которые по-разному используют Youtube, соцсети и слушают музыку, то можно сделать тарифы, которые учитывают их интересы. Предполагаю, что операторы связи так и поступают, выпуская линейки тарифов с дифференциацией оплаты по типу трафика.

Что еще можно проанализировать в имеющихся данных? Есть несколько кейсов с оборудованием абонентов. Оператор знает модель устройства абонента и может, например, предлагать определенные услуги только пользователям Samsung. Или, зная координаты базовых станций, можно нарисовать тепловую карту распределения телефонов Samsung (у меня нет реальных координат, поэтому карта к действительности не имеет отношения):

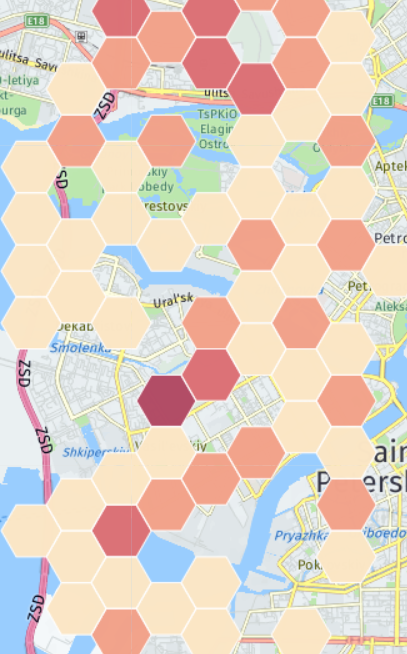
Может так получиться, что в каком-то регионе их окажется в процентном отношении больше, чем в других. Тогда эту информацию можно предложить Samsung-у для проведения рекламных акций или открытия салонов по продаже смартфонов. Далее можно посмотреть, на Top моделей устройств, с которых абоненты заходят в интернет:

Для маскировки современного положения вещей была взята устаревшая база IMEI, но сути подхода это не меняет. По списку видно, что большинство устройств — это Apple, модемы и Samsung-и, в конце появляются Meizu, Micromax и Xiaomi.

Собственно, это все применения исходным данным, которые я смог найти за короткое время. Конечно, по этим данным можно смотреть на разнообразные статистики и временные ряды, анализировать выбросы т.п., но вот так чтобы выявить какую-нибудь зависимость средствами машинного обучения… к сожалению, я не нашел пока, как это сделать.

Таким образом, вывод по исследованию Телеком данных такой: для полноценного решения задач оператора связи нужны данные из всех имеющиеся информационных систем, т.к. только имея доступ ко всем данным, можно эффективно стоить модели.

Общие выводы

• В первичном анализе данных никакой магии нет. Все основано на нескольких простых алгоритмах, понять и применять которые можно на интуитивном уровне.
• Но конечно, остаются и сложные задачи, решить которые можно только имея опыт и глубокие знания статистики, алгоритмом машинного обучения и программирования.