Логарифмируй это: метод логарифмической производной в машинном обучении

Прием, о котором пойдет речь — метод логарифмической производной — помогает нам делать всякие штуки, используя основное свойство производной от логарифма. Лучше всего этот метод зарекомендовал себя в решении задач стохастической оптимизации, которые мы исследовали ранее. Благодаря его применению, мы нашли новый способ получения стохастических градиентных оценок. Начнем с примера использования приема для определения оценочной функции.

Довольно математично.

Оценочная функция (score function)

Метод логарифмической производной — это применение правила для градиента к параметрам ? логарифма функции p(x;?):

$\$\$$display$$?? log p(x;?)=??p(x;?)/p(x;?)$$display$$

Применение метода оказывается удачным, когда функция p(x;?) является функцией правдоподобия, т. е. функция f с параметрами ? представляет собой вероятность случайной величины x. В этом частном случае функция

$$

называется оценочной, а правая часть представляет собой отношение оценок. Функция оценки имеет ряд полезных свойств:

Основная операция для оценки максимального правдоподобия. Максимальное правдоподобие является одним из главных принципов машинного обучения, используемых в обобщенной линейной регрессии, глубоком обучении, ядерных машинах, уменьшении размерности и тензорных разложениях, и т.д. Оценка необходима в решении всех этих задач.

Матождание оценки равно нулю. Наше первое использование метода логарифмической производной это покажет:

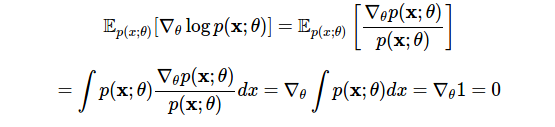В первой строке мы применили производный логарифм, а во второй поменяли порядок дифференцирования и интегрирования. Данное тождество обнаруживает нужный нам тип вероятностной гибкости: оно позволяет вычитать любой член из оценки, имеющей нулевое ожидание, при этом изменение не повлияет на ожидаемый результат (см. далее: контрольные переменные).

Дисперсия оценки — это информация Фишера, используемая для определения нижней границы Крамера-Рао.


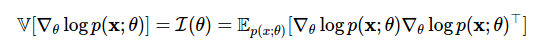
Теперь мы можем переходить в одной границе от градиентов логарифмической вероятности к градиентам вероятности и обратно. Однако главный злой герой сегодняшнего поста — сложный ожидаемый градиент из Способа 4 — возникает снова. Мы можем использовать нашу новую силу (функцию оценки) и найти еще одно умное оценочное решение для этого класса проблем.

Блок оценки оценочной функции

Наша задача — вычислить градиент математического ожидания функции f: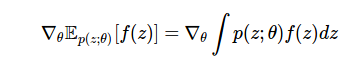


Это часто встречающаяся задача машинного обучения, необходимая для последующего вычисления в вариационном выводе, функции значений и обучении политикам (стратегиям) в обучающем процессе с подкреплением, ценообразовании производных инструментов в финансовой инженерии, учете запасов в исследованиях операций, и т.д.

Вычислить этот градиент трудно, так как интеграл обычно неизвестен, а параметры ? , относительно которых мы вычисляем градиент, имеют распределение p(z;?). Кроме того, нам может понадобиться вычислить этот градиент для недифференцируемой функции. Используя метод логарифмической производной и свойства функции оценки, мы можем вычислить этот градиент более удобным способом:

Выведем это выражение и рассмотрим его последствия для нашей задачи оптимизации. Для этой цели мы будем использовать еще один часто встречающийся метод — метод вероятностной идентичности, согласно которому мы умножим наши выражения на 1 — число, образованное делением плотности вероятности на саму себя. Объединив этот метод с методом логарифмической производной, мы получим блок оценки оценочной функции градиента:


В этих четырех строках мы произвели множество операций. В первой строке мы заменили производную интегралом. Во второй — применили наш вероятностный метод, который позволил сформировать коэффициент оценки. Используя логарифмическую производную, мы заменили этот коэффициент градиентом логарифмической вероятности в третьей строке. Это дает нам желаемую стохастическую оценку в четвертой строке, которую мы вычислили методом Монте-Карло, предварительно взяв выборку из p(z), а затем вычислив взвешенный градиентный член.

Это несмещенная оценка градиента. Наши предположения в этом процессе были несложными:

• Замена интегрирования дифференцированием действительна. Это трудно показать в общем плане, но сама замена обычно не вызывает никаких проблем. Мы можем подтвердить корректность этого приема, сославшись на формулу Лейбница и анализ приведенный здесь [1].
• Функция f(z) не должна быть дифференцируемой. Так мы сможем оценивать ее или наблюдать изменения значений для заданного z.
• Получение выборок из распределения p(z) не представляет сложности, так как это необходимо для оценки интеграла методом Монте-Карло.

Как и многие другие наши приемы, путь, который мы выбрали здесь, был уже пройден во многих других исследовательских областях, и в каждой области уже имеется свой термин, история разработки метода и круг задач, связанных с формулировкой проблемы. Приведем примеры:

1. Блок оценки оценочной функции (Score function estimator)

Наш вывод позволил нам преобразовать градиент ожидания в ожидание функции оценки

$$

что делает его удобным для обозначения таких оценок как блоки оценочной функции [2]. Это довольно распространенный термин, и я предпочитаю применять именно его.

Много проницательных наблюдений и ряд исторически важных разработок по теме изложены в работе под названием "Оптимизация и анализ чувствительности компьютерных имитационных моделей методом оценочной функции".

2. Методы отношения правдоподобия

Одним главных популяризаторов этого класса оценки стал П.В. Глинн [3]. Он интерпретирует отношение оценки

$\$\$$display$$??p(z;?)/p(z;?)$$display$$

как отношение правдоподобия и описывает блоки оценки как методы отношения правдоподобия. Я полагаю, что это несколько нестандартное использование термина «отношение правдоподобия». Оно обычно представляет собой отношение одной и той же функции при разных параметрах, а не отношение разных функций при одном и том же параметре. Поэтому я предпочитаю термин «Блок оценки оценочной функции». Многие авторы, и, в частности, например Майкл Фу [4], говорят о методах отношения правдоподобия и оценки (LR/SF). Наиболее важные работы по теме: "Оценочное отношение коэффициента правдоподобия для стохастических систем", где Глинн подробно объясняет важнейшие свойства дисперсии, и Оценка градиента Майкла Фу.

3. Автоматизированный вариационный вывод

Вариационный вывод трансформирует трудно решаемые интегралы, возникающие в байесовском анализе, в задачи для стохастической оптимизации. Неудивительно, что в этой области также появляются блоки оценки оценочных функций известные под разными терминами: вариационный стохастический поиск, автоматический вариационный вывод, вариационный вывод по модели «черного ящика», нейронный вариационный вывод — и это лишь те немногие, о которых мне известно.

4. Вознаграждение и градиенты стратегии

Для решения задач обучения с подкреплением мы можем сопоставить функцию f с вознаграждением, полученным от среды, распределение p(z;?) с политикой, а оценку — с градиентом политики или, в отдельных случаях, с характерным возможным выбором (characteristic eligibility).

Интуитивно это можно объяснить следующим образом: любые градиенты политики, которые соответствуют высоким вознаграждениям, получают большие веса за счет подкрепления со стороны блока оценки. Следовательно, блок оценки назван REINFORCE (ПОДКРЕПЛЕНИЕ) [5] и это обобщение в данный момент формирует теорему градиента стратегии (политики).

Контрольные переменные

Чтобы выполнить эту оценку по методу Монте-Карло эффективно, мы должны сделать ее дисперсию как можно меньше. В противном случае от градиента не будет никакой пользы. Добиться большего контроля дисперсии можно благодаря использованию модифицированную оценки:


где новый член ? называется контрольной переменной, широко используемой для уменьшения дисперсии в оценках по методу Монте-Карло. Контрольная переменная — это любой дополнительный член добавляемый в оценку, имеющую нулевое среднее значение. Такие переменные можно вводить на любом этапе, поскольку они не влияют на ожидания. Контрольные переменные влияют на дисперсию. Основной проблемой при использовании оценок является выбор контрольной переменной. Самый простой способ — использовать постоянный параметр, однако имеются и другие методы: разумные схемы выборки (например, антитетические или стратифицированные), дельта-методы или адаптивные постоянные параметры. Одно из самых всесторонних обсуждений источников дисперсии и методов уменьшения дисперсии приведено в этой книге П. Глассермана [6]

Группы стохастических систем оценки

Сравните сегодняшнюю оценку с той, которую мы вывели, используя метод линейной производной в методе 4.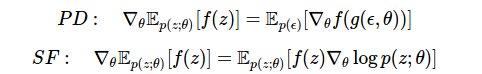

Здесь у нас есть два эффективных подхода. Мы можем:

• дифференцировать функцию f, используя линейные производные, если функция дифференцируема, или
• дифференцировать плотность p(z), используя функцию оценки.

Существуют и другие способы создания стохастических градиентных оценок, но эти два являются наиболее распространенными. Их можно легко комбинировать, что позволяет нам использовать наиболее подходящую оценку (обеспечивающую самую низкую дисперсию) на разных этапах наших вычислений. Решить такую задачу, в частности, можно за счет использования стохастического вычислительного графа.

Заключение

Метод логарифмической производной позволяет нам чередовать нормировано вероятностные и логарифмически вероятностные представления распределений. Он составляет основу определения функции оценки, и служит способом максимально правдоподобной оценки и важного асимптотического анализа, сформировавших большую часть наших статистических знаний. Важно отметить, что данный метод может использоваться для оценки градиента общего назначения в решении задач стохастической оптимизации, лежащих в основе многих важных проблем машинного обучения, с которыми мы сталкиваемся в настоящее время. Оценки градиента по методу Монте-Карло необходимы для подлинно универсального машинного обучения, к которому мы стремимся. Для этого важно понимать закономерности и методы, лежащие в основе такой оценки.

---