Аппроксимация математических функций нейронной сетью

Всем привет. Начал я активно изучать нейронные сети, и решил похвастаться в этой статье, чему я уже научился.

На мой взгляд самое простое с чего нужно начинать изучать нейросети — это аппроксимация таких простых математических функций, как синус, квадратичная функция, экспонента и т.д. Согласно универсальной теореме аппроксимации — нейронная сеть с одним скрытым слоем может аппроксимировать любую непрерывную функцию многих переменных с любой точностью. Главное чтобы в этой сети было достаточное количество нейронов. И еще важно удачно подобрать начальные значения весов нейронов. Чем удачнее будут подобраны веса, тем быстрее нейронная сеть будет сходиться к исходной функции.

Исходя из этого, я решил проверить эту теорему на практике, и написал вот такую вот программу:

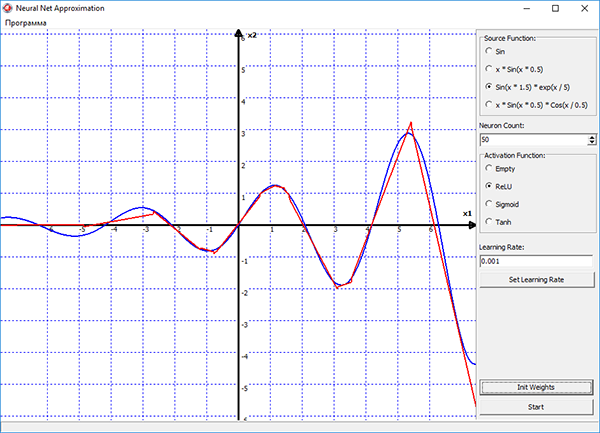Обучение сети в программе, осуществляется методом стохастического градиентного спуска, который реализован в виде алгоритма обратного распространения ошибки. Процесс обучения наглядно отображается на графике в программе. Синим цветом на графике показана исходная функция, красным — функция построенная нейронной сетью. Можно выбирать различные функции активации для нейронов скрытого слоя, подбирать скорость обучения и изменять количество нейронов прямо в процессе обучения. И смотреть в реальном времени как изменение этих параметров влияет на процесс обучения сети.

Сама нейросеть имеет следующую структуру:


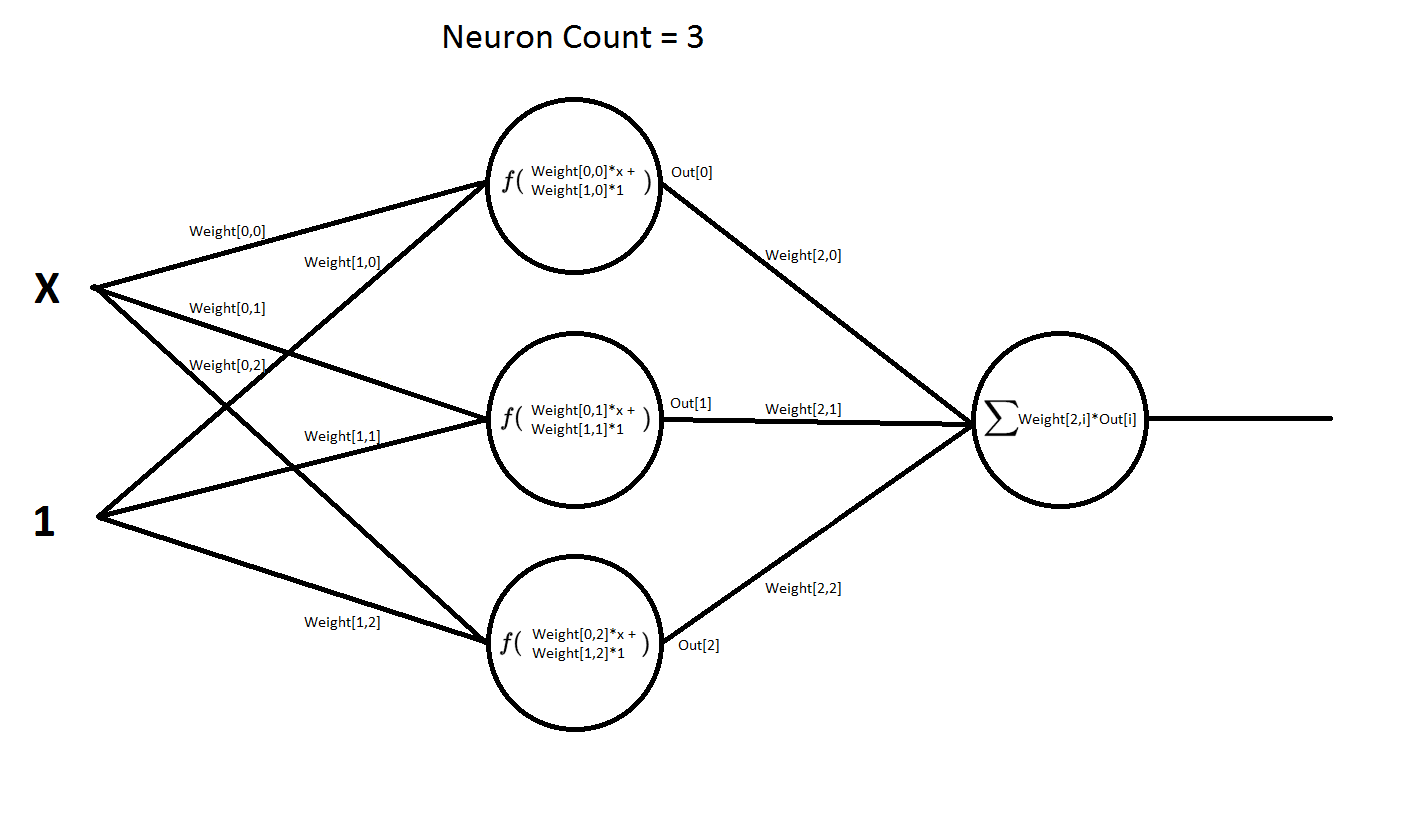
То есть она имеет два входа и один выход. Первый вход x — это значения функции, которые она может принимать по оси x. На второй вход всегда подается единица. В терминах нейросетей такой вход называется входом смещения. При его наличии сеть намного быстрее обучается и намного быстрее сходится к нужному нам результату. Эта сеть имеет два слоя слой, скрытый и выходной. На данной схеме показана сеть, которая содержит 3 нейрона в скрытом слое. Но в программе число этих нейронов можно менять в реальном времени, т.е. прямо в процессе обучения сети. Во втором же слое, число нейронов всегда неизменно. Т.е. там всегда один нейрон.

В нейронах в скрытого слоя применяется активационная функция — это может быть и выпрямитель «ReLU», сигмоид и гиперболический тангенс. Так же можно вообще убрать оттуда функцию активации «Empty», и там по сути там останется один сумматор. Будет интересно посмотреть как поведет себя сеть, не имея в себе нелинейных функций.

В нейроне второго слоя функции активации нет. Там обычный сумматор. Если бы там тоже была функция активации, то мы бы уже не смогли построить график функции нейронной сети.

Ну давайте теперь посмотрим, как это теперь всё будет работать в программе. Для начала попробуем аппроксимировать самую простою функцию синус. Поставим функцию активации на empty, то есть в нейронов скрытого слоя у нас не будет функции активации, а только сумматор. Поставим скорость обучения 00.1, Проинициализируем веса начальными случайными значениями, нажимаем кнопку старт и видим следующую картину:

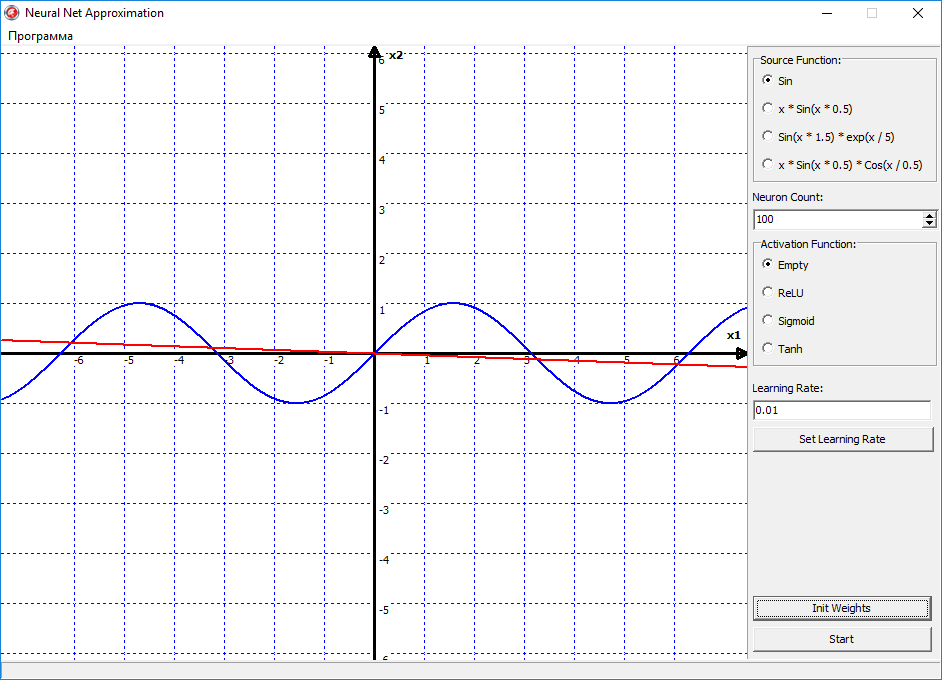Красная линия начала дрыгаться, а это значит пошло обучение. Но теперь, как бы мы не меняли настройки программы, кол-во нейронов или скорость обучения, эта дрыгающаяся линия так и остаётся линией. Почему? Да всё очень просто. Потому что в нейронах скрытого слоя нет активационных функций, то есть нет нелинейности в нейронной сети, и на выходе она всегда будет давать прямую линию. Этот пример я показал специально, что в нейросети обязательно должна присутствовать нелинейность, иначе сеть будет выдавать всегда вот такой результат, и в итоге ничему не обучиться.

Теперь давайте попробуем переключить функцию активации на ReLU «выпрямитель», и посмотрим что будет:

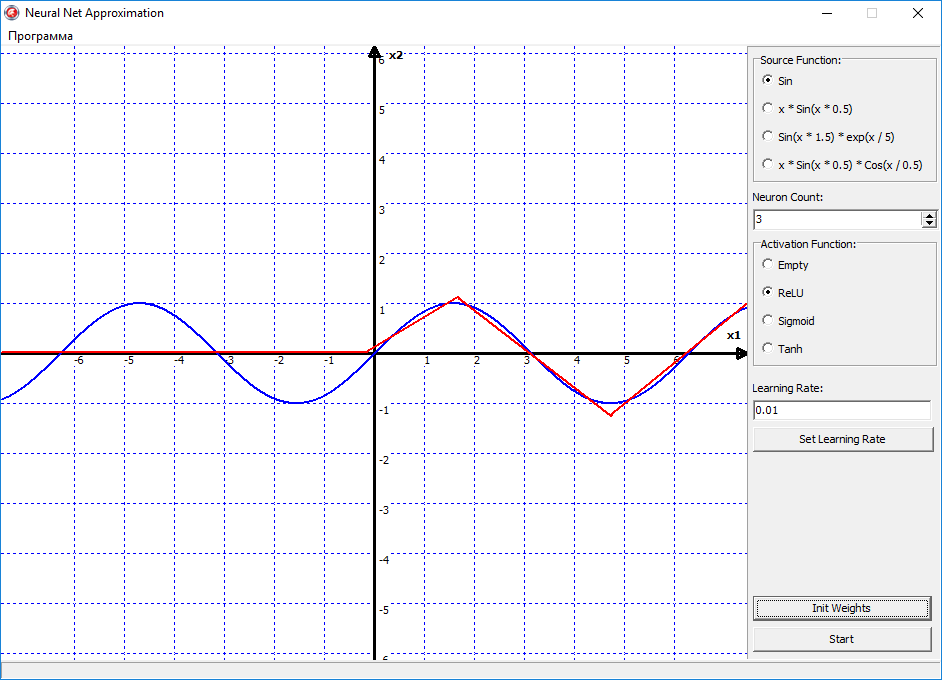Ну вот видно, что тут уже поинтереснее начинается поведения сети, и эта линия начала выгибаться, то есть появилась нелинейность в сети. По сути, правую часть синуса, сеть уже аппроксимировала успешно. Давайте пробовать увеличивать количество нейронов, и наблюдать за изменениями:

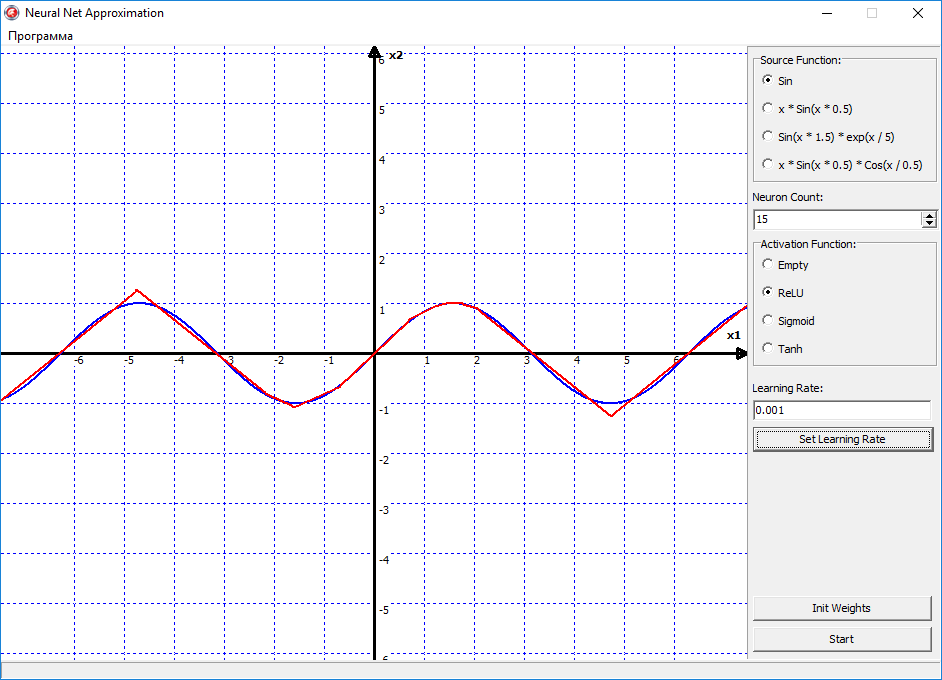Теперь стало еще интересней, получается, что 15 нейронов в принципе хватило, чтобы более-менее аппроксимировать функцию синуса. На этом графике можно видеть, что ReLU — это всё таки грубая функция активации, то есть она ломает нашу прямую линию на множество мелких отрезков, с острыми углами. То есть если мы будем увеличивать количество нейронов, то функция будет становиться более гладкой, за счёт увеличения числа переломов, которые ломают линию на отрезки. Но преимущество ReLU в том, что это очень простая функция. И имеет очень простую производную. Соответственно скорость вычислений существенно возрастает. Поэтому ReLU можно использовать там, где не важна высокая точность, а важно скорость работы нейронной сети.

Но давайте теперь переключим функцию активации на сигмоид, и смотрим что получилось:

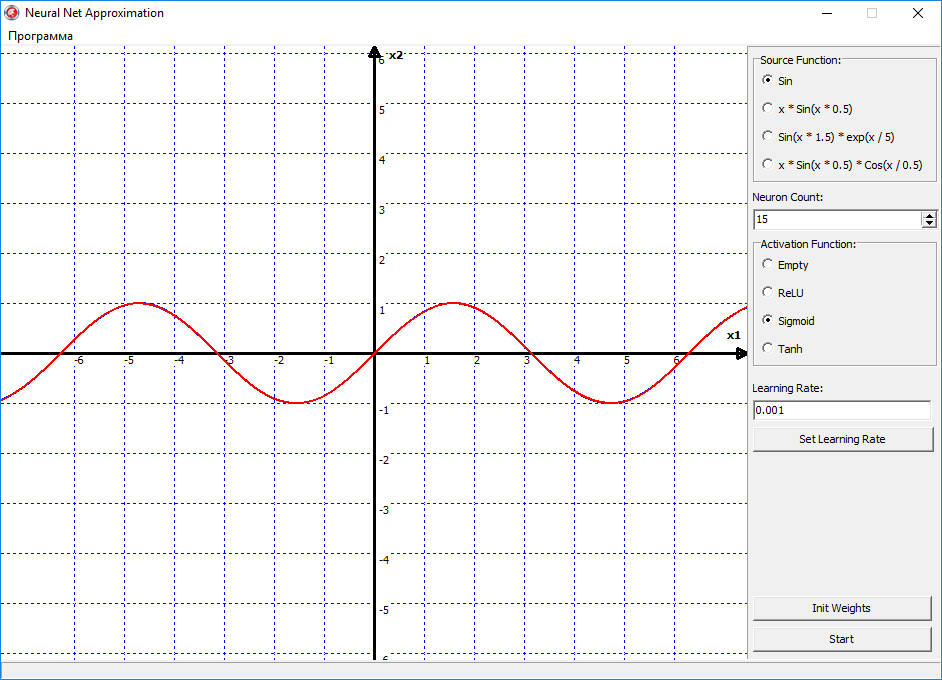Вуаля, и сеть с идеальной точность аппроксимировала функцию синуса. Все из-за того, что сигмоид — это более гладкая функция активации. И имеет более высокую точность. В отличии от ReLU, она не ломает прямую, как если бы вы взяли в руки две соломинки, и сломали их пополам. Сигмоид же сгибает эту линию, как сгибается металлическая проволока, в отличии от хрупкой соломинки. Но конечно же недостаток сигмоида в том, что его скорость вычисления ее существенно больше.

Также если теперь переключить функцию активации на гиперболический тангенс. Сеть тоже с идеальной точностью ее аппроксимирует. Но отличие тангенса от сигмоида в том, что тангенс на выходе дает диапазон значений от -1 до 1. А сигмоид от 0 до 1. Поэтому тут уже нужно смотреть, какая функция будет лучше подходить под какую-то конкретную задачу. То есть если в вашей задачи нужно чтобы нейросеть выдавал значения от нуля до единицы, то соответственно подойдет больше сигмоид, если от минус единицы до единицы, то тангенс.

Можно также экспериментировать с аппроксимацией не только синуса, но других, совершенно различных функций. Сеть будет аппроксимировать их без проблем:


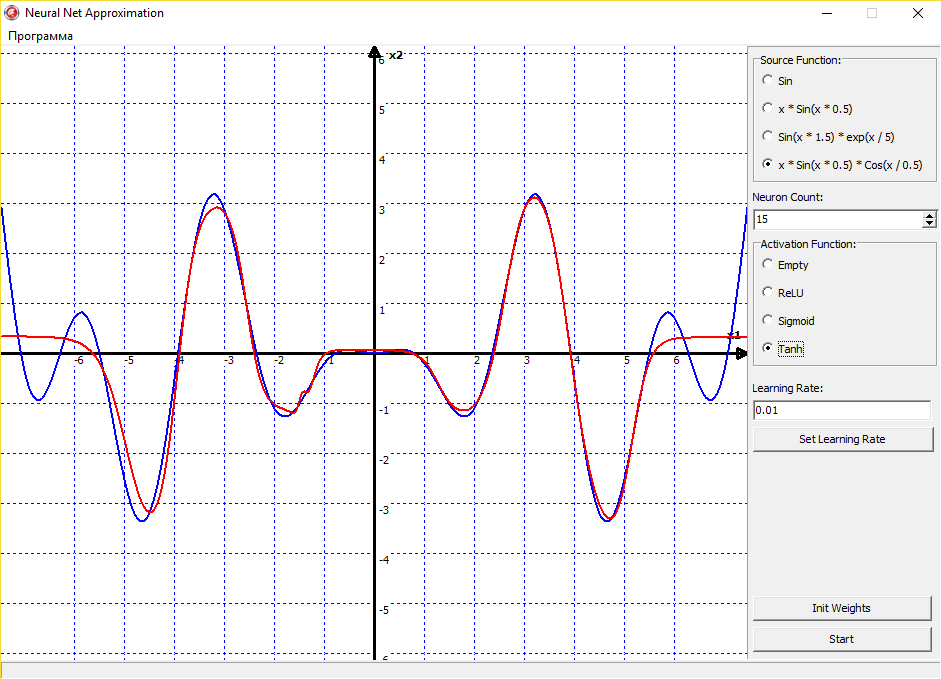
Выходит, что универсальная теорема аппроксимации действительно верна, и нейронная сеть может аппроксимировать функцию с любой точностью. Тут остается главным только правильный подбор функции активации, скорости обучения и правильная инициализация начальных значений весов. Со всем этим надо экспериментировать, нарабатывать опыт и тренировать свою интуицию. Поскольку нет какого-то четкого правила обучения нейронных сетей. Все зависит от опыта программиста, ну и еще от везения.