Прикладное применение задачи нелинейного программирования
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2017-05-15 16:32

Закончив специалитет и готовясь к защите кандидатской диссертации, я задался вполне логичным вопросом: «а что же дальше?» Имея за плечами опыт как обычной работы, так и исследовательской, я вновь вернулся к той самой идее, которая, казалось бы, должна была утонуть под толщей пыли. Но вернулся я к этой идее в более осознанной форме.
Я решил заняться разработкой программного обеспечения, связанного с той отраслью, которой занимаюсь уже на протяжении 8 лет, и моими личными академическими пристрастиями, которые включают в себя методы оптимизации и машинное обучение.
 Ну что ж, всем заинтересовавшимся:
Ну что ж, всем заинтересовавшимся: Занимаясь реализацией программного обеспечения для своего диплома (и впоследствии диссертации), я подходил к этому вопросу «в лоб»: меня не волновало, насколько создаваемая система будет гибкой, как легко она будет модифицируема. Желание получить результат здесь и сейчас вкупе с неопытностью приводили к тому, что код постоянно приходилось переписывать, что, конечно же, не влияло положительно на профессиональное развитие. Уже сейчас я понимаю, что, как бы ни хотелось, нельзя сломя голову бросаться решать задачу. Надо вникнуть в ее суть, оценить имеющиеся знания, понять, чего недостает, сопоставить понятия предметной области классам, интерфейсам и абстракциям. Словом, нужно осознать имеющиеся резервы и грамотно подойти к проектированию архитектуры программного приложения.
Как вы уже догадались, эта статья будет посвящена разработке и описанию первых элементов будущего приложения.
Определение подхода к разработке и формулировка основной задачи
На Хабре есть большое количество статей, посвященных методологиям разработки ПО. Например, в этой достаточно понятно описаны основные подходы. Остановимся подробнее на каждом из них:- «Waterfall Model» — не подходит по причине как минимум того, что четко определенных требований у меня нет, есть лишь набор идей, между которыми придется впоследствии наладить взаимодействие,
- «V-Model» — не подходит по той же причине,
- «Incremental Model» — более подходящая по сравнению с предыдущими модель, однако тут так же требуется подробная формализация
- «RAD Model» — модель, которая больше подходит команде опытных специалистов,
- «Agile Model» — отлично подходит по критерию отсутствия необходимости конкретизации требований, а также по гибкости в процессе разработки,
- «Iterative Model» — несмотря на то что в работе указана необходимость четкого определения целей, идейно такая модель кажется близкой (учитывая слова «Основная задача должна быть определена, но детали реализации могут эволюционировать с течением времени»),
- «Spiral Model» — направлена для реализации больших проектов, к которым вряд ли можно отнести предполагаемое ПО.
Я буду стараться придерживаться концепций модели «Agile». На каждую итерацию разработки будет предлагаться определенный набор целей и задач, которые будут подробнее освещаться в статьях.
Итак, на данный момент имеется следующая формулировка общей задачи: разрабатываемое программное обеспечение, должно реализовывать различные алгоритмы оптимизации (как и классические аналитические, так и современные эвристические) и машинного обучения (алгоритмы классификации, кластеризации, редукции размерности пространства, регрессии). Итоговой финальной целью является разработка методик применения данных алгоритмов в области синтеза оптимального управления и создания торговых стратегий на финансовых рынках. В качестве основного языка для разработки был выбран Scala.
Итак, в этой работе я расскажу:
- О задаче оптимизации и причинах ее выбора в качестве основополагающего объекта изучения,
- Об основных абстракциях и их реализациях, которые позволят использовать подход, основывающийся на решении прикладных задач путем сведения к задаче оптимизации,
- Об алгоритме K-Means, простейшем алгоритме Random Search и как заставить их дружить и работать на благо единой цели.
Оптимизация
Вследствие того что большую часть своей исследовательской практики я посвятил решениям задачи оптимизации, мне будет удобней оперировать именно с этой точки зрения. Обычно под решением задачи оптимизации, как бы это банально и косноязычно ни звучало, понимается поиск некоторого «оптимального» (с точки зрения условий задачи) объекта. Понятия «оптимальности» варьируются от одной предметной области к другой. Например, в задаче поиска минимума функции требуется найти точку, которой соответствует наименьшее значение целевой функции, в задача мета-оптимизации требуется определить параметры алгоритма, при которых он дает наиболее точный результат/наиболее быстро отрабатывает/дает наиболее стабильный результат, в задаче синтеза оптимального управления требуется синтезировать контроллер, позволяющий перевести объект в терминальное состояние за наименьшее время и т.д. Уверен, что каждый специалист сможет продолжить это список задачами, связанными с его профессиональной сферой. В математике, особое внимание уделяется задаче нелинейного программирования, к которой можно свести большое количество других прикладных задач. В общем случае, для постановки задачи нелинейного программирования требуется задать:- произвольную функцию (она выполняет роль некоторого критерия качества: для задач минимизации требуется найти вектор, которому соответствует наименьшее значение, для максимизации — наоборот),
- набор ограничений, которые по сути определяют область допустимых значений аргумента оптимизируемой функции.
Таким образом, суть данной задачи можно описать следующим образом: требуется найти в области поиска вектор, обеспечивающий минимальное/максимальное значение целевой функции.
Существует огромное количество алгоритмов решения этой задачи. Условно их можно разделить на две группы:
- аналитические алгоритмы:
- имеют более узкий круг решаемых задач в связи с тем, что могут накладывать ограничения на компоненты задачи,
- могут вводить в задачу объекты более высокого уровня (например, производные определенного порядка),
- несомненным достоинством таких методов является то, что по большей части они позволяют гарантированно получить результат определенной точности.
- эвристические алгоритмы:
- отсутствует свойство гарантированности вычислений, т.е. нельзя быть уверенным в том, что полученное решение попало хотя бы в область притяжения локального экстремума,
- имеют меньшую вычислительную сложность, что дает возможность их применения с целью получения практически приемлемого результата за приемлемое время (например, на задачах большой размерности, когда получение ответа с помощью аналитического алгоритма может занять сутки).
В принципе, эвристические алгоритмы можно воспринимать как способ направленного перебора. В этой группе вы можете обнаружить достаточно известные генетические алгоритмы, алгоритм симуляции отжига, различные популяционные алгоритмы. Большое количество алгоритмов объясняется достаточно просто: нет универсального алгоритма, который был бы хорош одновременно для всех типов задач. Кто-то лучше справляется с выпуклыми функциями, другой направлен на работу с функциями, обладающими овражной структурой линий уровня, третий специализируется на многоэкстремальных функциях. Как и в жизни — у всего есть своя специализация.
Используемые абстракции
На основе приведенных ранее рассуждений мне кажется, что проще всего работать с двумя понятиями: преобразование и алгоритм. На них и остановимся подробнее.Преобразования (Transformations)
Вследствие того что почти любую процедуру/функцию/алгоритм можно рассматривать как некоторое преобразование, будем оперировать с этим объектом как с одним из базовых. Предлагается следующая иерархия между различными типами преобразований: Остановимся на элементах поподробнее:
Остановимся на элементах поподробнее:- Неоднородное преобразование (Inhomogeneous Transformation) — самый общий вид преобразования, когда классы входного и выходного объекта могут быть различными,
- Однородное преобразование (Homogeneous Transformation) — частный вид неоднородного преобразования, когда классы входного и выходного объекта одинаковые,
- Векторная функция (Vector Function) — преобразование, которой трансформирует вектор, состоящий из элементов множества A, в другой вектор, состоящий из элементов того же множества,
- Функция (Function) — аналогична векторной функции (за исключением того, что выходной элемент теперь является скаляром),
- Метрика (Metric) — некоторое оценивающее преобразование, ставящее в соответствие объекту числовое значение.
Код класса неоднородного преобразования
class InhomogeneousTransformation[A, B](transform: A => B) extends Serializable { def apply(a: A): B = transform(a) def *[C](f: InhomogeneousTransformation[B, C]) = new InhomogeneousTransformation[A, C](x => f(transform(x))) } Видно, что он содержит всего два метода, один из которых реализует процедуру составления композиции нескольких преобразований (только в не совсем привычном порядке). Это в дальнейшем понадобится для создания более сложных преобразований из простых.
Код класса однородного преобразования
class HomogeneousTransformation[A](transform: A => A) extends InhomogeneousTransformation[A, A](transform) { } Здесь два параметра типа были свернуты в один.
Код класса векторной функции
class VectorFunction[A <: Algebra[A]] (transform: Vector[A] => Vector[A])(implicit converter: Double => A) extends HomogeneousTransformation[Vector[A]](transform) { } Налицо измененная параметризация обобщенного класса. Теперь данный параметр определяет то, из объектов какого класса будет состоять преобразуемый вектор. Следует отметить ограничение, накладываемое на класс, что определяется данным кодом "[A <: Algebra[A]]". Ограничение выражается в следующем: объекты, из которых составляется вектор, должны поддерживать основные арифметические операции и их можно использовать как аргумент привычных элементарных функций (показательных, тригонометрических и т.п.). Подробный код можно будет посмотреть на исходниках, которые выложены на github'e (ссылка будет в конце работы).
Коды класса Function и способа его неявного приведения к неоднородному преобразованию
class Function[A <: Algebra[A]] (transform: Vector[A] => A)(implicit converter: Double => A) extends VectorFunction[A](x => Vector("result" -> transform(x))) { def calculate(v: Vector[A]): A = transform(v) } object Function { implicit def createFromInhomogeneousTransformation[A <: Algebra[A]] (transformation: InhomogeneousTransformation[Vector[A], A])(implicit converter: Double => A) = new Function[A](x => transformation(x)) } Код класса метрики и соответствующие преобразования
class Metric[A](transform: A => Real) extends InhomogeneousTransformation[A, Real](transform) { } object Metric { implicit def createFromInhomogeneousTransformation[A](transformation: InhomogeneousTransformation[A, Real]) = new Metric[A](x => transformation(x)) implicit def toFunction (metric: Metric[Vector[Real]])(implicit converter: Double => Real): Function[Real] = new Function[Real](x => metric(x)) } Алгоритм
Я думаю, что естественным будет определить алгоритм как набор трех операций: инициализация, итеративная часть и терминация. На вход алгоритма подается некоторое задание (Task). В ходе инициализации происходит генерация начального состояния (State) алгоритма, которое модифицируется в ходе повторения итеративной части. В конце с помощью процедуры терминации из последнего состояния алгоритма создается объект, соответствующий типу R выходного параметра алгоритма.Код класса алгоритм
trait GeneralAlgorithm[T <: GeneralTask, S <: GeneralState, R] { def initializeRandomly(task: T): S def initializeFromSeed(task: T, seed: S): S final def initialize(task: T, state: Option[S]): S = { state match { case None => initializeRandomly(task) case Some(seed) => initializeFromSeed(task, seed) } } def iterate(task: T, state: S): S def terminate(task: T, state: S): R def prepareFolder(log: Option[String]): Unit = { if (log.isDefined) { val temp = new File(log.get) if (!temp.exists() || !temp.isDirectory()) temp.mkdir() else { if (temp.exists() && temp.isDirectory()) { def prepare(file: File): Unit = if (file.isDirectory()) { file.listFiles.foreach(prepare) file.delete() } else file.delete() prepare(temp) } } } } def logState(log: Option[String], state: S, fileId: Int): Unit = { log match { case Some(fileName) => { val writer = new ObjectOutputStream(new FileOutputStream(s"${fileName}/${fileId}.st")) writer.writeObject(state) writer.close() } case None => () } } final def work(task: T, terminationRule: S => Boolean, seed: Option[S] = None, log: Option[String] = None): R = { prepareFolder(log) var currentState = initialize(task, seed) var id = 0 logState(log, currentState, id) val startTime = System.nanoTime() while (!terminationRule(currentState)) { currentState = iterate(task, currentState) id = id + 1 currentState.id = id currentState.timestamp = 1e-9 * (System.nanoTime() - startTime) logState(log, currentState, id) } terminate(task, currentState) } } Из предыдущего описания задачи нелинейного программирования ясно, что задание (Task) для алгоритма оптимизации состоит из функции и области поиска (пока ограничимся простым случаем, когда область поиска задается многомерным параллелепипедом).
case class OptimizationTask[A <: Algebra[A]](f: Function[A], searchArea: Map[String, (Double, Double)]) extends GeneralTask { def apply(v: Vector[A]): A = f.calculate(v) } abstract class OptimizationState[A <: Algebra[A]] extends GeneralState { def getCurrentBest(optimizationTask: OptimizationTask[A])(implicit cmp: Ordering[A]): Vector[A] } class MultiPointOptimizationState[A <: Algebra[A]](points: Seq[Vector[A]]) extends OptimizationState[A] { override def toString: String = { s"ID: ${id} " + s"Timestamp: ${timestamp} " + points.zipWithIndex.map{ case (point, id) => s"# ${id} ${point} "}.mkString(" ") } override def getCurrentBest(optimizationTask: OptimizationTask[A])(implicit cmp: Ordering[A]): Vector[A] = points.minBy(point => optimizationTask(point)) def apply(id: Int): Vector[A] = points(id) def size: Int = points.size } class OnePointOptimizationState[A <: Algebra[A]](point: Vector[A]) extends MultiPointOptimizationState(points = Seq(point)) { override def getCurrentBest(optimizationTask: OptimizationTask[A])(implicit cmp: Ordering[A]): Vector[A] = point def apply(): Vector[A] = point } abstract class OptimizationAlgorithm[A <: Algebra[A], S <: OptimizationState[A]] extends GeneralAlgorithm[OptimizationTask[A], S, Vector[A]] { } K-Means VS. Random Search
Что ж, первые два пункта обещанной программы освещены, пора переходить к третьему. Оба алгоритма хорошо описаны в различных источниках, поэтому я думаю, что у читателей не составит труда разобраться с ними. Вместо этого я проведу параллели к описанным ранее абстракциям.class Task(val vectors: Seq[Vector[Real]], val numberOfCentroids: Int) extends GeneralTask { def apply(id: Int): Vector[Real] = vectors(id) def size: Int = vectors.size def toOptimizationTask(): (OptimizationTask[Real], InhomogeneousTransformation[Vector[Real], kCentroidsClusterization]) = { val varNames = vectors.head.components.keys.toSeq val values = vectors.flatMap(_.components.toSeq) val searchAreaPerName = varNames.map { name => val accordingValues = values .filter(_._1 == name) .map(_._2.value) (name, (accordingValues.min, accordingValues.max)) } val totalSearchArea = Range(0, numberOfCentroids) .flatMap { centroidId => searchAreaPerName .map { case (varName, area) => (s"${varName}_${centroidId}", area) } }.toMap val varNamesForCentroids = Range(0, numberOfCentroids) .map { centroidId => (centroidId, varNames.map { varName => s"${varName}_${centroidId}" }) } .toMap val splitVector: InhomogeneousTransformation[Vector[Real], Map[Int, Vector[Real]]] = new InhomogeneousTransformation( v => Range(0, numberOfCentroids) .map { centroidId => (centroidId, Vector(v(varNamesForCentroids(centroidId)) .components .map { case (key, value) => (key.dropRight(1 + centroidId.toString.length), value) })) }.toMap) val vectorsToClusterization: InhomogeneousTransformation[Map[Int, Vector[Real]], kCentroidsClusterization] = new InhomogeneousTransformation(v => new kCentroidsClusterization(v)) val clusterizationForMetric: InhomogeneousTransformation[kCentroidsClusterization, (kCentroidsClusterization, Seq[Vector[Real]])] = new InhomogeneousTransformation(clusterization => (clusterization, vectors)) val quality: Metric[Vector[Real]] = splitVector * vectorsToClusterization * clusterizationForMetric * SquareDeviationSumMetric (new OptimizationTask(f = quality, searchArea = totalSearchArea), splitVector * vectorsToClusterization) } } val quality: Metric[Vector[Real]] = splitVector * vectorsToClusterization * clusterizationForMetric * SquareDeviationSumMetric (new OptimizationTask(f = quality, searchArea = totalSearchArea), splitVector * vectorsToClusterization) Простейшее описание алгоритма случайного поиска можно посмотреть на википедии. Отличия в реализованной версии заключаются в том, что генерируется не одна точка из текущей, а несколько, а также вместо нормального распределения используется равномерное.
Кластеризатор, построенный с помощью алгоритма K-Means однозначно определяется своими центроидами. Сам алгоритм K-Means представляет собой постоянную замену текущих центроид новыми центроидами, рассчитанными как среднее значение всех векторов в отдельно взятых кластерах. Таким образом, в любой момент времени состояние алгоритма K-Means можно представить как набор векторов.
Таким образом, кластеризатор может быть построен либо напрямую с помощью алгоритма K-Means, либо с помощью решения задачи поиска оптимального кластеризатора, обеспечивающего минимум суммарного расстояния точек кластеров от соответствующих центроид.
Сгенерируем несколько синтетических наборов данных размерности 2, 3 и 5.
Генерация нормально распределенной случайной величины
f[mu_, sigma_, N_] := RandomVariate[#, N] & /@ MapThread[NormalDistribution, {mu, sigma}] // Transpose Num = 100; sigma = 0.1; data2D = Join[ f[{0.5, 0}, {sigma, sigma}, Num], f[{-0.5, 0}, {sigma, sigma}, Num] ]; ListPlot[data2D] Export[NotebookDirectory[] <> "data2D.csv", data2D, "CSV"]; 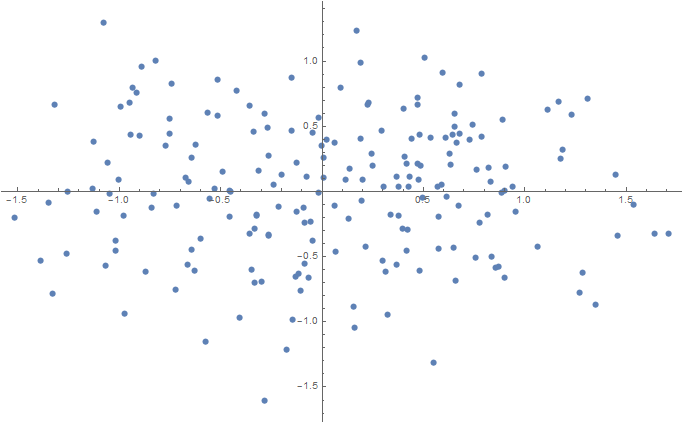
Num = 100; mu1 = 0.0; sigma1 = 0.1; mu2 = 2.0; sigma2 = 0.2; mu3 = 5.0; sigma3 = 0.3; data3D = Join[ f[{mu1, mu1, mu1}, {sigma1, sigma1, sigma1}, Num], f[{mu2, mu2, mu2}, {sigma2, sigma2, sigma2}, Num], f[{mu3, mu3, mu3}, {sigma3, sigma3, sigma3}, Num] ]; dimReducer = DimensionReduction[data3D, Method -> "TSNE"]; ListPlot[dimReducer[data3D]] Export[NotebookDirectory[] <> "data3D.csv", data3D, "CSV"]; 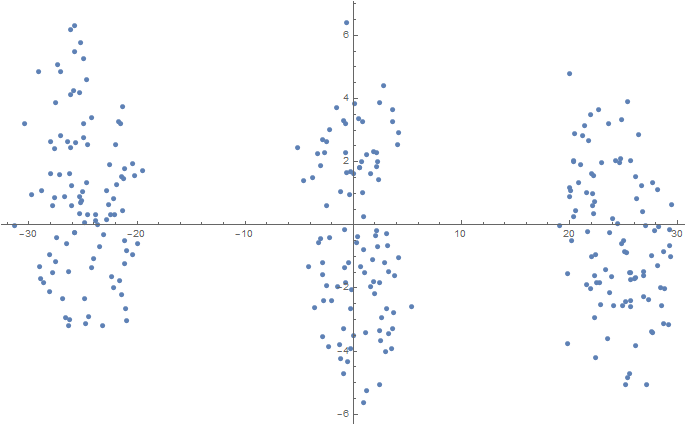
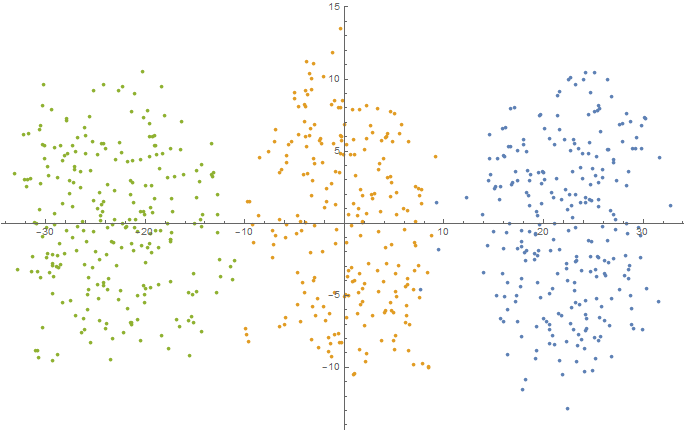
Num = 250; mu1 = -2.5; sigma1 = 0.9; mu2 = 0.0; sigma2 = 1.5; mu3 = 2.5; sigma3 = 0.9; data5D = Join[ f[{mu1, mu1, mu1, mu1, mu1}, {sigma1, sigma1, sigma1, sigma1, sigma1}, Num], f[{mu2, mu2, mu2, mu2, mu2}, {sigma2, sigma2, sigma2, sigma2, sigma2}, Num], f[{mu3, mu3, mu3, mu3, mu3}, {sigma3, sigma3, sigma3, sigma3, sigma3}, Num] ]; dimReducer = DimensionReduction[data5D, Method -> "TSNE"]; ListPlot[dimReducer[data5D]] Export[NotebookDirectory[] <> "data5D.csv", data5D, "CSV"]; 
И «прогоним» их через оба алгоритма построение кластеризатора. Полученные результаты сведем в таблицу:
| 2D | 3D | 5D | |
|---|---|---|---|
| Clusterization Quality (via K-Means): | 90.30318857796479 | 96.48947132305597 | 1761.3743823022821 |
| Clusterization Quality (via Optimization): | 87.42370021528419 | 96.4552486768293 | 1760.993575500699 |


По таблице видно, что даже несложный алгоритм оптимизации может успешно решить задачу построения простейшего кластеризатора. При этом созданный кластеризатор будет оптимальным (а если честно, то субоптимальным, так как используемый метод оптимизации не гарантирует нахождение точки глобального оптимума) с точки зрения используемой метрики качества. Естественно, для задач большей размерности используемый алгоритм оптимизации уже вряд ли подойдет (тут лучше пользоваться более сложными и эффективными алгоритмами, основывающимися на нескольких эвристиках разного уровня). Для небольшой же синтетической задачи Random Search справился достаточно хорошо.
Вместо послесловия
Хочется поблагодарить всех, кто прочитал статью, отписался в комментариях. Словом, всех, кто внес свой вклад в создание данной работы. Наверное, следует сразу отметить, что статьи на эту тематику будут появляться по мере возможностей и моей текущей загруженности. Но мне хочется сказать, что на этот раз я постараюсь довести начатое мной дело до конца. Ссылки и литератураИсточник: habrahabr.ru