Генетический советник для торговли опционами

При торговле опционами одна из главных задач состоит в определении справедливой цены опциона. На основании нее можно понять какие опционы недооценены рынком, а какие переоценены в данный момент. Исходя из этого и принимаются решения о покупке или продаже конкретного опциона. В данной статье рассматривается опыт создания советника в основе которого лежит Генетический Алгоритм (ГА), позволяющего как раз автоматизировать процесс выбора опционов для продажи и покупки соответственно Советник, в отличие от торговых роботов (или Механических Торговых Систем — МТС), не производит сделок, он лишь дает рекомендации трейдеру, который уже самостоятельно принимает решение совершать сделку или нет.

Для начала — пару слов о генетическом алгоритме:

Подробно описывать генетический алгоритм не имеет смысла, поскольку эта тема хорошо представлена и на данном ресурсе и вообще на просторах Интернета. Остановлюсь только на основных моментах, которые необходимы для понимания концепции генетического советника в целом.

Итак, генетический алгоритм можно рассматривать как направленный случайный поиск оптимального решения, какой либо задачи. Для примера, рассмотрим целевую функцию вида:

$\$\$display\$\$\; S=F(X\_1,X\_2,...X\_n)\; (1)\; \$\$display\$\$$

Где: S — значение функции F от нескольких аргументов X1..Xn. Допустим что все аргументы X лежат в некотором диапазоне целочисленных значений от -100 до 100. Чтобы найти максимальное (оптимальное) значение S, необходимо подобрать такое сочетание аргументов X при котором функция F и будет максимальной. При небольшом количестве аргументов задачу можно решить аналитически, однако при увеличении количества аргументов сложность такого решения существенно возрастает. Теоретически, задачу можно решить и методом перебора возможных решений, при условии, что все аргументы X целочисленные. Однако, при диапазоне аргументов от -100 до 100 и количестве аргументов 10 число возможных решений примерно равно

$\$\$display\$\$1.076*10^\{23\}\$\$display\$\$$

Если предположить что для вычисления одного варианта требуется 1 наносекунда то для перебора всех вариантов компьютеру понадобится несколько миллионов лет! Т.е. решение перебором в таком виде нежизнеспособно. Тут и приходит на помощь генетический алгоритм, суть которого заключается в том, что все аргументы функции кодируются в двоичном виде. Для кодирования одного аргумента с диапазоном -100:100 (или 201 возможное значение) нам потребуется 8 бит (один ген), $\$inline\$2^8=256\$inline\$$ (ближайшее двоичное значение больше чем 201), итого для кодирования всех 10 аргументов нам нужно использовать 80 бит. Эта двоичная последовательность называется генотипом (хромосомой) (в генетическом алгоритме используются термины из биологии). Первоначально создается популяция из случайных генотипов. Т.е. в нашем случае создается несколько двоичных последовательностей (допустим 20) каждая из которых имеет длину 80 бит и которые заполняются 0 и 1 случайным образом.

Далее для каждой особи (двоичной последовательности) мы рассчитываем значение функции и отбираем те особи которые показывают максимальные значения (к примеру, первые 10 максимальных значений из 20) целевой функции (аналог естественного отбора, выживают те кто наиболее приспособлен). Для отобранных особей проводим процедуру скрещивания, мутации и создаем новое поколение особей, которые уже более приспособлены чем первоначальная популяция, из которой вновь выбираем наиболее приспособленные особи. Проводя такой цикл несколько раз мы последовательно «выращиваем» генотип который приближает нас к максимальному значению целевой функции. Стоит отметить что вариантов отбора, скрещивания и мутации генотипов существует достаточно много, кроме того существует проблема локальных максимумов, вырождения популяции, но эти вопросы выходят за рамки данной статьи и рекомендованы для самостоятельного изучения.

Опционы

Опционы это производные финансовые инструменты с нелинейной стоимостью. В основе опционов лежит Базовый Актив (БА). Опционы бывают 2-х видов опционы CALL, стоимость которых увеличивается с РОСТОМ цены БА и опционы PUT, стоимость которых увеличивается при СНИЖЕНИИ цены БА. Для расчета теоретической цены опциона используется знаменитая формула Блэка-Шоулза. На российском рынке БА для опционов является соответствующий фьючерс. Так для опционов на доллар США, БА является фьючерс (Si) на доллар США. У опционов, также как и фьючерсов, есть срок жизни. Дата, когда опцион заканчивает свое существование, называется датой экспирации. В этот момент производится окончательный расчет по опционам которые есть у трейдера в корзине.

Несмотря на сложность этих инструментов они обладают свойствами которых нет у других финансовых инструментов. Одна из таких особенностей заключается в том, что они позволяют по сути торговать одновременно один и тоже инструмент (базовый актив) но на разных ожидаемых ценах (страйках), это дает возможность выстраивать сложные комбинации из опционов разных типов (CALL/PUT) и разных цен (страйков).

Условно, торговлю опционами можно разделить на 2 типа: статический и динамический.

При статической торговле, трейдер делает некоторое предположение относительно цены БА в будущем, и в зависимости от этого выстраивает позицию. Например, если трейдер считает что цена останется в некотором диапазоне, то он может продать опционы CALL и PUT и заработать на полученной премии от продажи. Однако, если цена БА приблизится к краю такой позиции, то ее необходимо «регулировать» что бы не получить убыток.

При динамической торговле, делается ставка не на конкретное движение цены БА, а на колебание цены, т.е. волатильность. При высокой волатильности цены на опционы могут значительно изменяться, что дает возможность для заработка.

Рассматриваемая концепция торговли опционами с помощью ГА относится к статической торговле, на которой и остановимся поподробнее.

«Дешевые» и «Дорогие» опционы

Итак, представим трейдера, который делает предположение что доллар США в ближайшее время подорожает и он хочет на этом заработать с использованием опционной позиции. Трейдер покупает 10 опционов CALL со страйком 56000 по цене 1800 руб за опцион. В этом случае позиция трейдера будет иметь вид представленный на Рис.1.

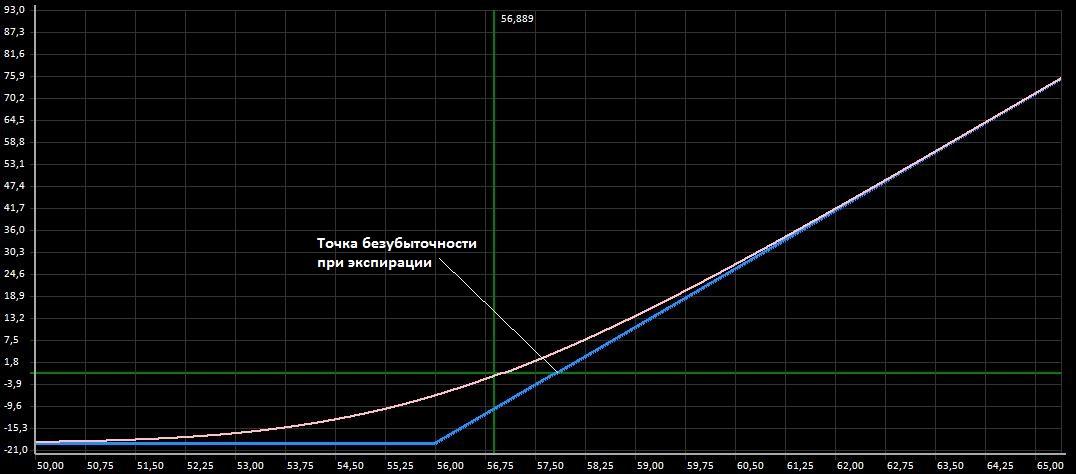Рис.1. Купленные опционы CALL

Из которой видно что позиция будет прибыльной если к моменту экспирации цена БА будет больше чем 57800, в противном случае позиция будет убыточной, и максимальный убыток составит 18000 руб. Для уменьшения максимального убытка трейдер решает продать еще 10 опционов CALL со страйком 58000 по цене 905 руб. В этом случае позиция будет иметь вид представленный на Рис.2. Такая позиция называется «бычий CALL-Спрэд».

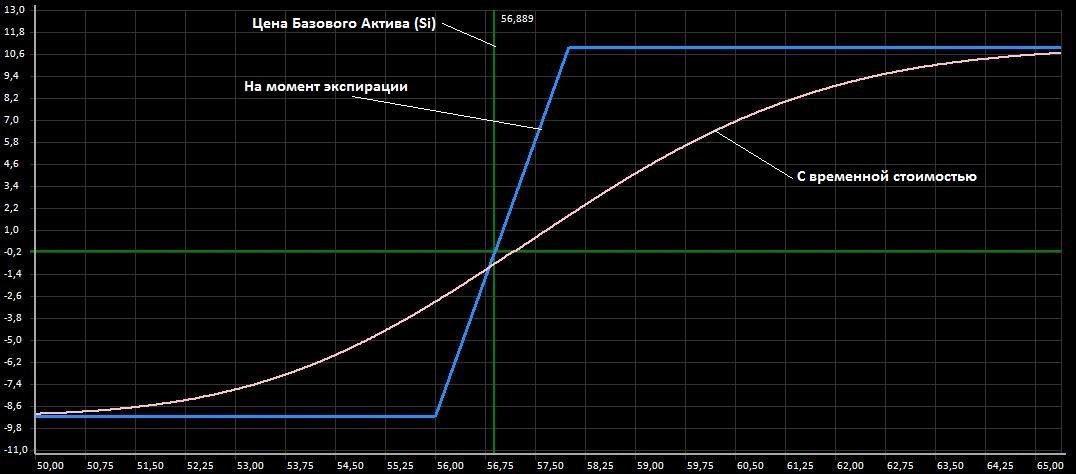Рис.2. Бычий CALL-Спрэд

Максимальный убыток сокращается до 8950 руб но при этом и максимальная прибыль становится ограниченной, точка безубыточности смещается левее.

Теперь представим что опционы со страйком 56000 переоценены рынком и были куплены по цене 2000 руб, а опционы со страйком 58000, наоборот неодоценены и проданы по 700 руб, тогда позиция будет иметь вид:

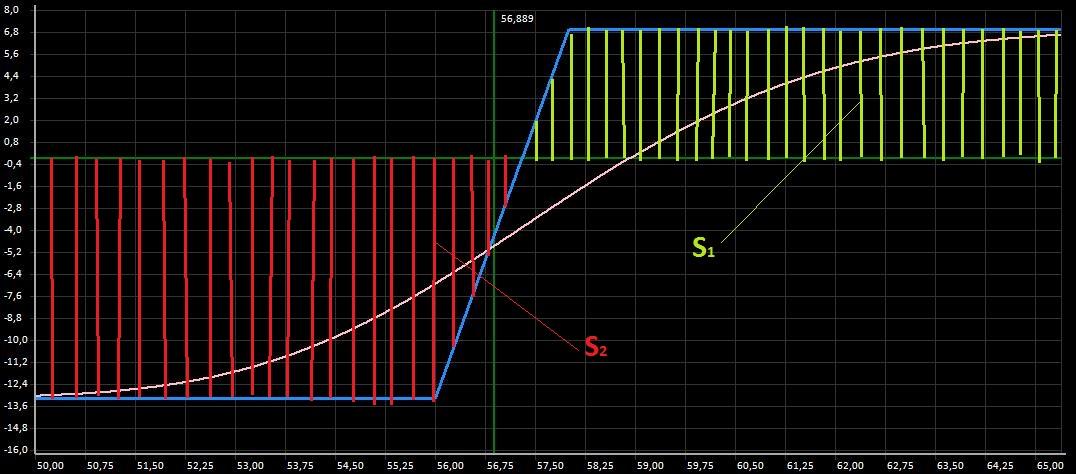Рис.3. Купили дороже, продали дешевле

Рассмотрим противоположную ситуацию, когда трейдеру удалось купить опционы дешевле (1500 руб) а продать дороже (1200 руб) тогда позиция имела бы вид:

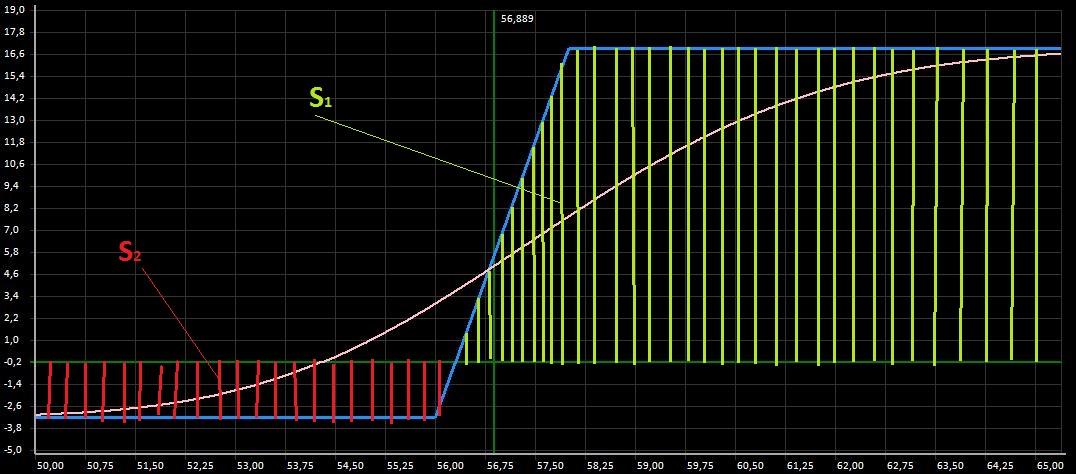Рис.4. Купили дешевле, продали дороже.

Анализируя графики на рисунках 2,3 и 4 становится очевидным что «положительная» площадь графика S1 увеличивается, а «отрицательная» S2 уменьшается пропорционально тому чем дешевле опционы мы покупаем и дороже продаем. Другими словами стремясь купить недооцененные (дешевые) опционы и продать переоцененные (дорогие) мы увеличиваем «положительную» площадь позиции –S1 и уменьшаем «отрицательную» — S2. Таким образом качество опционной позиции формально можно оценивать по размеру площади S1. Идеальный случай когда S1 максимальна а S2 отсутствует вовсе.

Кроме того, можно выдвинуть гипотезу, что при ограниченном размере Гарантийного Обеспечения (ГО) позиции и заданном диапазоне страйков, в каждый момент времени теоретически существует такое сочетание купленных и проданных опционов при котором «положительная» площадь позиции будет максимальной.

В общем виде «положительную» площадь можно представить как функцию суммы площадей купленных и проданных опционов разных страйков:

$\$\$display\$\$S\_1=F(X\_1,X\_2...X\_n)\; (2)\$\$display\$\$$

Где: X1..Xn – количество проданных/купленных опционов на каждом страйке Нетрудно заметить, что функция площади S1 (2) соответствует целевой функции ГА (1) рассмотренного выше. Т.е. применительно для опционной позиции размер «положительной» площади и будет являться целевой функцией. Для нахождения максимально возможной «положительной» площади позиции с ГО, например, не более 100000 руб можно перебрать все возможные комбинации опционов, однако, как было показано ранее, это занимает катастрофически много времени, поэтому использование ГА для поиска оптимальной позиции (по критерию максимальной «положительной» площади) вполне оправдано.

Необходимо добавить, что такой подход можно применять не только для формирования начальной позиции, но и для регулирования существующей. Поскольку цены на рынке все время меняются то возможно появление такой ситуации когда покупка или продажа опционов приведет к увеличению «положительной» площади текущей позиции. В этом случае целевая функция будет иметь вид:

$\$\$display\$\$S\_1=F\_0(Z\_1,Z\_2,...Z\_k)\; +\; F(X\_1,X\_2,...X\_n)\; (3)\$\$display\$\$$

Где: F0 – это функция суммы площадей существующей позиции, Z1..Zk — количество проданных/купленных опционов на каждом страйке. Реализация

Таким образом, основная функция советника это поиск такого сочетания купленных/проданных опционов при котором «положительная» площадь позиции будет максимальной при заданной длине одного гена, т.е. при ограничении максимального количества опционов для одного страйка.

Сам советник написан на языке C# который выполняет все вычисления. Исходные данные для расчетов советник получает из терминала QUIK с помощью модуля написанного на языке Lua и коннектора написанного на C++. См. рис.5.

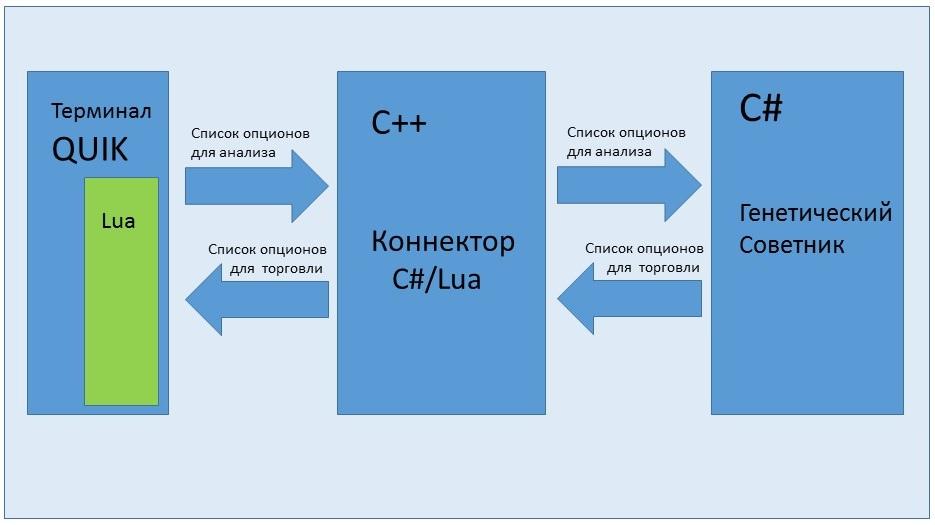Рис.5. Структурная схема советника.

Модуль Lua анализирует цены опционов и передает их в советник, причем нет смысла использовать все возможные страйки поскольку на многих страйках «жизни» почти нет (например, на очень дальних страйках). Поэтому для анализа используются только те опционы которые можно купить или продать с высокой вероятностью. После расчетов советник передает список опционов для покупки/продажи обратно в QUIK, где тот же модуль на Lua выставляет заявки и контролирует их исполнение.

Функционал советника позволяет строить график текущей позиции, выполнять генетический поиск оптимальной позиции, корректировать полученный результат вручную при необходимости, передавать данные для торговли обратно в QUIK. Вид советника представлен на Рис.6а. и 6в.

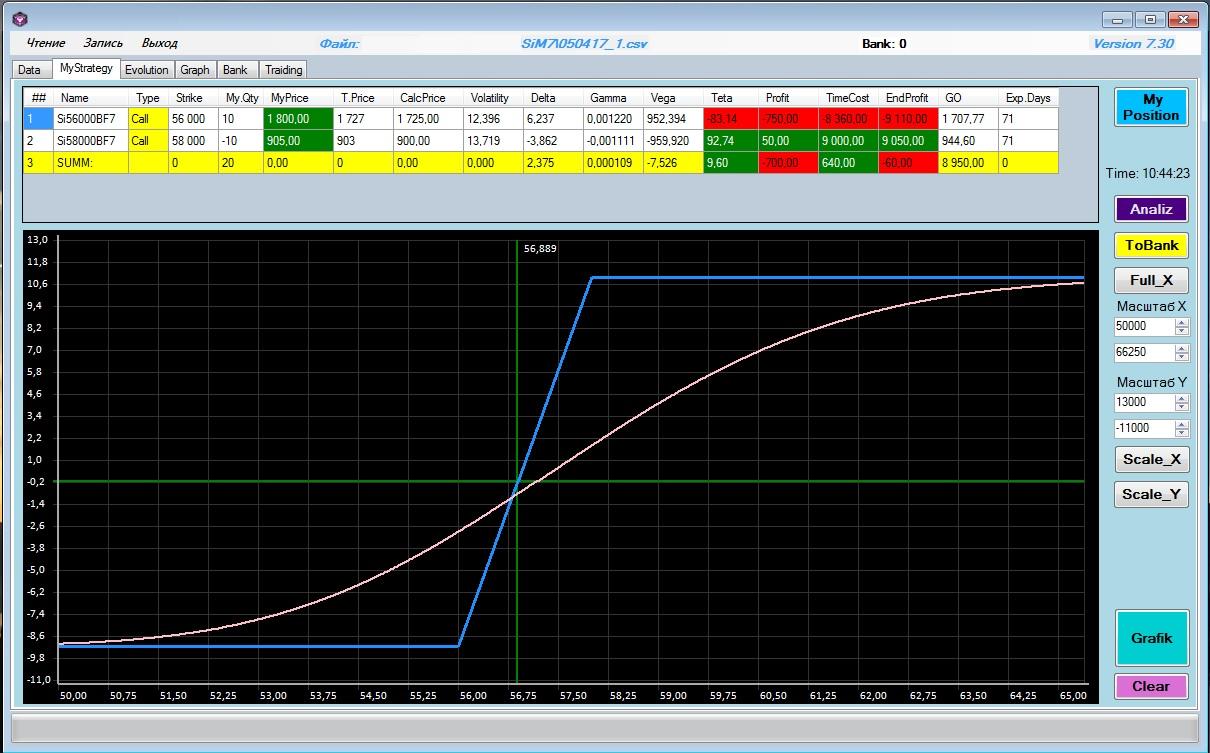Рис.6а. Интерфейс генетического советника

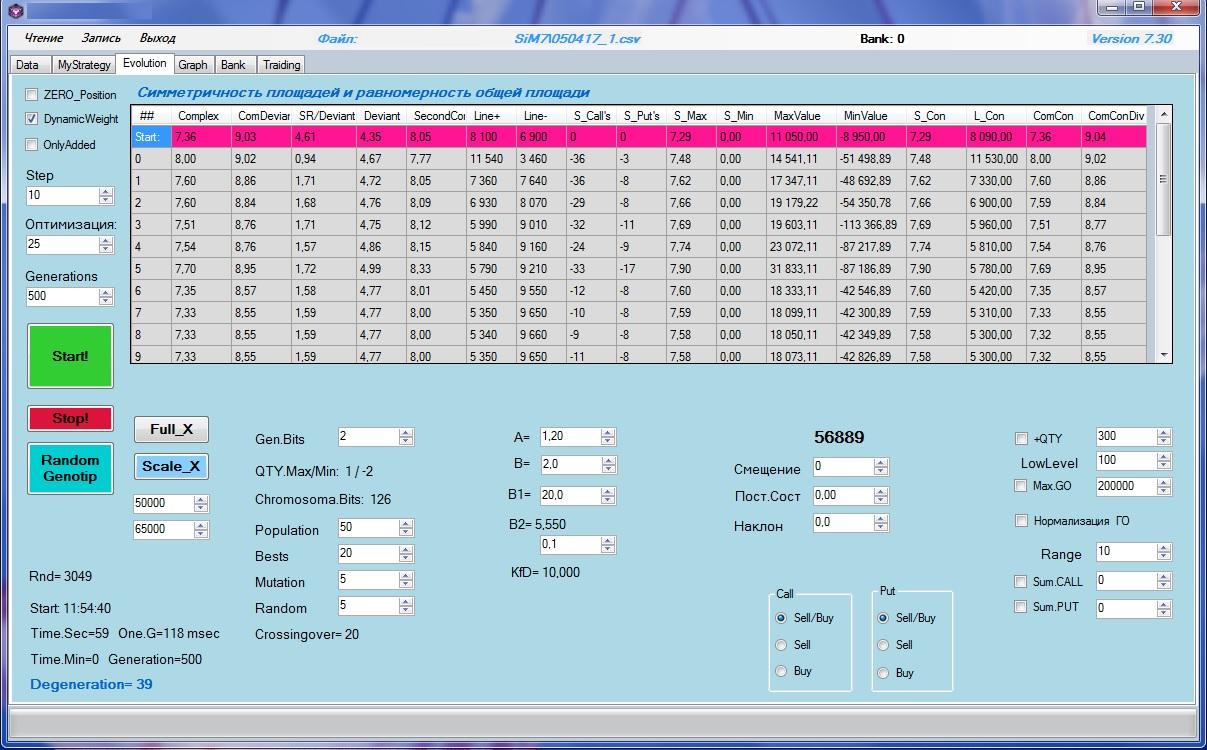Рис.6в. Настройки генетического алгоритма.

Подробнее о целевой функции

Мы выбрали в качестве целевой функции «положительную» площадь позиции, однако такой подход не отражает в полной мере «качество» опционной позиции. Где под качеством понимается соотношение доходность/риск. Например, при достаточно большой «положительной» площади «отрицательная» площадь может быть еще больше. Или, например, «положительная» площадь может быть вытянута вверх. Т.е. целевую функцию надо сделать более «умной» что бы она более эффективно отражала качество позиции. Один из простых вариантов это использовать соотношение «положительной» и «отрицательной» площадей — S1/S2. В этом варианте целевая функция будет увеличиваться и при увеличении положительной площади (доходность) и при уменьшении «отрицательной» (риск).

Первые «подводные камни»

Для оценки работы советника возьмем созданную позицию CALL-спрэд (Рис.2) и попытаемся ее улучшить с помощью советника. Через 1000 поколений получаем новую позицию – Рис.7.

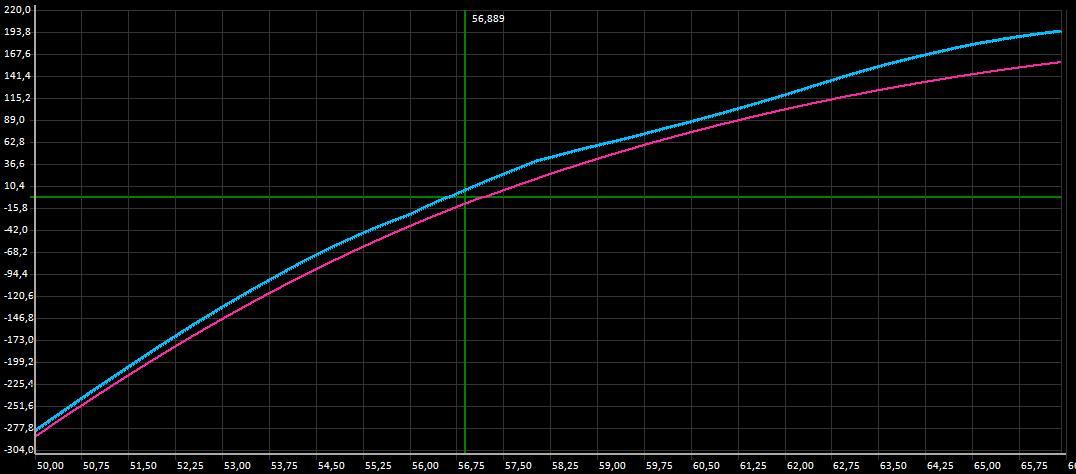Рис.7. Первый результат работы ГА.

Полученный результат, мягко говоря, не впечатляет, хотя формально ГА выполнил свою функцию размер «положительной» площади больше «отрицательной». Позиция стала отдаленно напоминать купленный синтетический фьючерс. Объясняется полученный график достаточно просто. Дело в том что для ГА нет разницы в какой области графика находится «положительная» площадь – на дальних страйках или на ближних. Но для реальной торговли важно что бы «положительная» площадь была сосредоточена вблизи текущей цены БА. Поскольку вероятность изменения цены на небольшую величину выше чем сильное движение цены (если, конечно, изначально не делалась ставка на сильное движение). В этой связи необходимо изменить расчет целевой функции таким образом, что бы площадь вблизи цены БА имела больший вес, чем площадь на дальних страйках. Для этого введем в расчет целевой функции динамический весовой коэффициент — Ks, который учитывает расположение площади относительно текущей цены БА. Площадь, фактически, является интегралом функции, который вычисляется в данном случае методом прямоугольников. При расчете, в каждой точке значение площади одного прямоугольника будем умножать на этот коэффициент. За основу коэффициента возьмем сигмоидную (логистическую) функцию но сделаем ее симметричной относительно текущей цены БА:

$\$\$display\$\$Ks(Страйк)=1/(1+e^\{Ax-B\})\; (4)\$\$display\$\$$

Где: A-коэффициент крутизны сигмоидной функции, B-коэффициент «ширины» — выбираются опытным путем. х(Страйк) — аргумент сигмоидной функции рассчитывается как:

$\$\$display\$\$\; x=ABS((Страйк-ЦенаБА)/(Шаг\; Страйка))(5)\; \$\$display\$\$$

Очевидно, что ценность дальних страйков будет падать по мере приближения даты экспирации. При текущей цене БА в 56000 пунктов и за 90 дней до экспирации велика вероятность что цена за 90 дней может увеличиться до 65000 пунктов или опуститься до 45000. Но если до экспирации остается, к примеру, 2 дня, то вероятность достижения цены уровня 65000 или 45000 с текущей цены 56000 существенно снижается. Поэтому динамический коэффициент должен учитывать время до экспирации, а также уровень текущей волатильности. Это можно сделать добавив в формулу известный коэффициент учитывающий оба эти параметра:

$\$\$display\$\$\; Волатильность/?\{Количество\; .дней.\; до.\; экспирации\}(6)\; \$\$display\$\$$

В результате получим семейство симметричных сигмоидных функций в зависимости от времени до экспирации и волатильности. Рис.8.
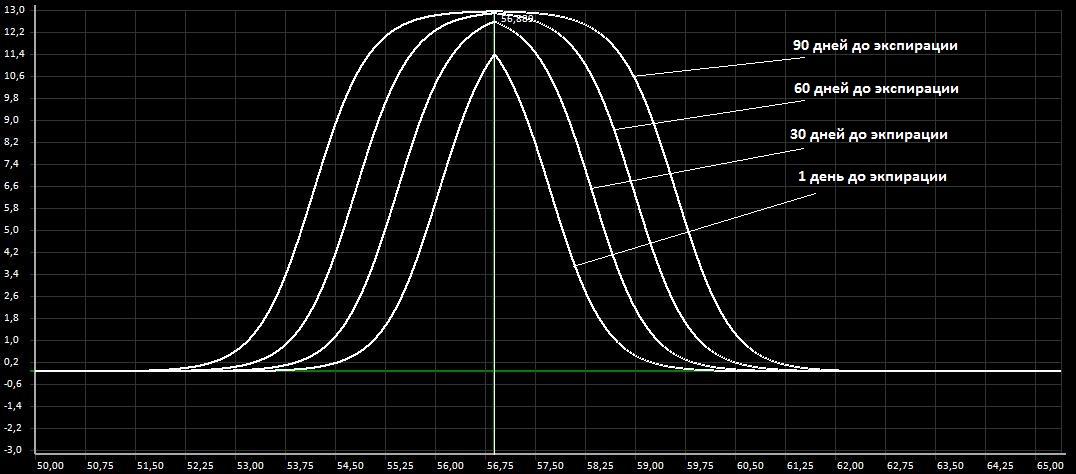
Рис.8. Семейство симметричных сигмоидных функций при различных сроках экспирации (при одном значении волатильности)

Теперь целевая функция настроена так что бы отдавать предпочтение площади которая находится вблизи цены БА с учетом времени до экспирации и текущей волатильности. После такого изменения эффективность позиции существенно улучшилась. На Рис.9. показан результат работы советника

Рис.9. Первоначальная позиция и позиция сформированная ГА при использовании динамического коэффициента Ks.

В результате работы ГА к имеющимся первоначально 20 контрактам, было добавлено еще 52 новых контракта (30 различных опционов), корзина теперь состоит из 72 контрактов, ГО около 37000 руб. Позиция стала интересней – в левой части отрицательная область отсутствует вообще, т.е. при понижении цены БА позиция остается в плюсе. Правая часть имеет ограничение по прибыли, и при цене БА выше 61500 позиция станет отрицательной, однако при увеличении цены БА можно повторно подобрать более выгодную позицию.

Кроме того, если в формулу (5) вместо цены БА подставить не текущую цену БА а ожидаемую, то фокус нашей целевой функции будет сдвинут именно в ожидаемую область. Допустим, что цена БА увеличится, исходя из ожиданий, подставим в формулу (5) значение 58889 (на 2000 пунктов больше текущей цены).

Тогда график сигмоидной функции и полученный результат будет иметь вид на Рис.10.

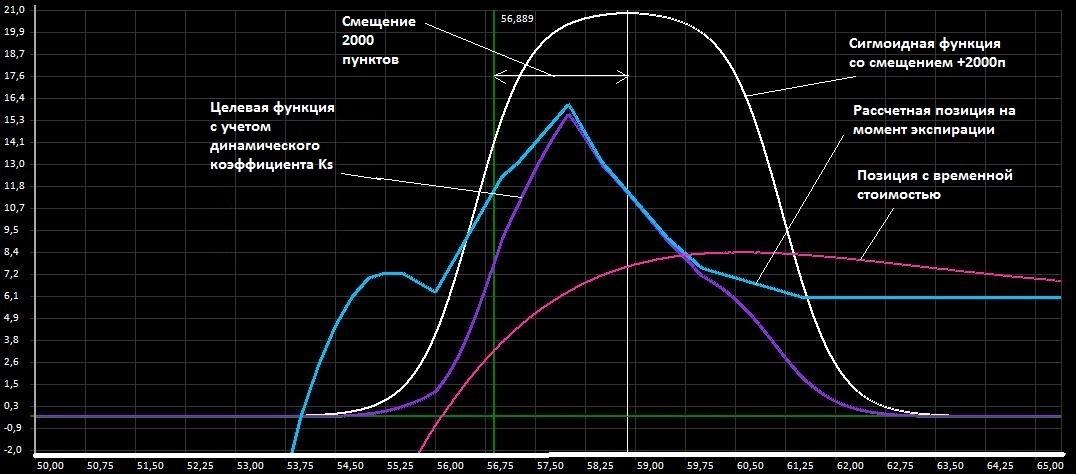Рис.10. Работа ГА со смещенной сигмоидной функцией на 2000 пунктов

На рисунке видно что новая позиция изменилась, теперь справа у нас нет отрицательной области. Таким образом оперируя коэффициентами A,B и смещением цены БА можно выстраивать новую позицию с акцентом в интересующей нас области.

Семейства позиций последовательно сформированных ГА с разным смещением сигмоидной функции на одних исходных данных изображены на Рис.11.

Рис.11.Семейство позиций с разными смещениями цены БА.

Еще раз о целевой функции и ограничениях

Форма позиций на Рис.11. отличается от предыдущих, поскольку использована другая целевая функция. Как показала практика создание целевой функции самая сложная задача – именно она определяет результат. Одна и та же целевая функция может давать разные результаты в разных состояниях рынка. Поэтому в советник добавлена возможность выбора различных целевых функций учитывающих несколько факторов: соотношение площадей S1/S2, соотношение длин участков где площадь положительна, непрерывность площади, равномерность распределения площади и т.д. Кроме того советник позволяет наложить некоторые ограничения на позицию, например, максимальный размер ГО, количество проданных (купленных) опционов и т.д.

Выводы

Практические испытания советника дают основания полагать что представленная концепция создания опционной позиции вполне имеет право на жизнь. Реальные тесты показали способность советника создавать эффективные стратегии.

К преимуществам, такой системы можно отнести автоматизированное формирование и регулирование позиции. ГА позволяет получить весьма «красивые» позиции опционов которые крайне затруднительно получить при «ручной» торговле (ввиду сложного сочетания большого количества разных опционов). ГА дает достаточно высокую сходимость. Если провести формирование позиции несколько раз на одних и тех же данных то результаты будут близки друг к другу.

Однако советнику требуется время на формирование позиции. ГА работает не так уж быстро, особенно при большом количестве опционов и длинной хромосоме. Кроме того, иногда приходится перебрать разные варианты целевых функций что бы построить приемлемую позицию в конкретной рыночной ситуации. За это время данные на основании которых строится позиция могут потерять актуальность. Поэтому производительность компьютера здесь выходит на первое место.

Самая большая проблема, это ситуация, когда экспирация уже близка, а цена БА находится у края позиции. В этом случае регулирование позиции становится затруднительным из-за резкого сокращения количество опционов которые можно использовать. Хотя ГА справляется и с этой задачей, но получаются рискованные позиции с высокой стоимостью ГО. Справедливости ради, надо отметить, что такая проблема существует и при торговле руками.

Спасибо всем кто дочитал до конца!