Комплексная нейронная сеть на основе ряда Фурье от функции многих переменных

Второй такой задачей является прогнозирование временных рядов с заданной точностью. Сети прямого распространения с сигмоидальной активационной функцией не дают возможности предсказать ошибку по количеству скрытых нейронов. Для того чтобы можно было предсказать эту ошибку стоит использовать какой-нибудь ряд для скорости сходимости которого есть расчетные формулы. В качестве такого ряда был выбран ряд Фурье.

Ряд Фурье

Комплексный ряд Фурье от одной переменной.

Но нейронные сети зачастую работают с функциями многих переменных. Предлагаю рассмотреть ряд Фурье от двух независимых переменных. [2]

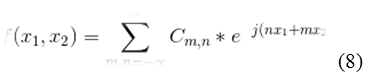
В общем случае следует использовать ряд Фурье для функций от «k» переменных.

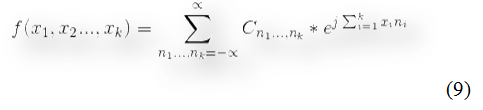Архитектура

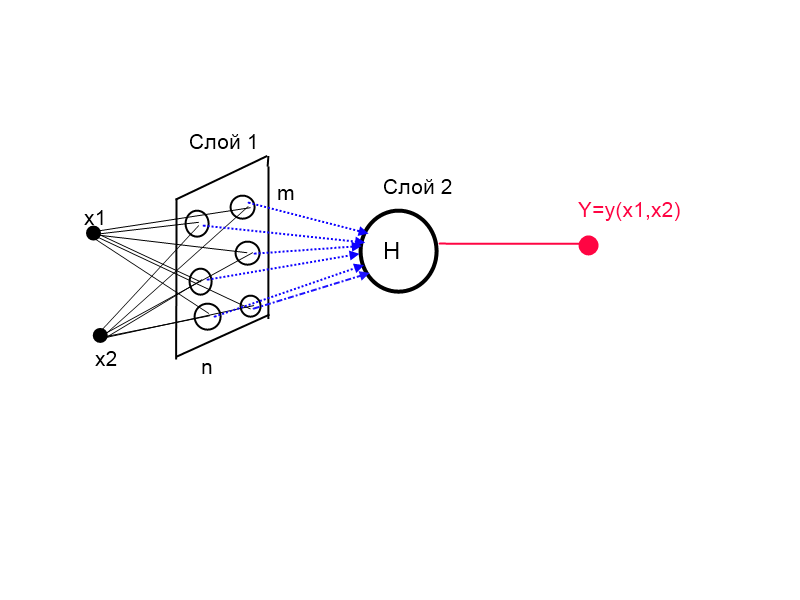
Рисунок 1. Архитектура комплексной сети (КИНСФ)

На рисунке 1 показана архитектура комплексной искусственной нейронной сети Фурье (КИНСФ), которая по сути реализует формулу 9. Здесь скрытый слой представляет собой матрицу нейронов mxn где m — число дескрипторов разложения Фурье, а n — размерность входного вектора. Веса в первом слое имеют физический смысл частот с наибольшей энергией, а веса второго слоя имеют смысл коэффициентов ряда Фурье. Таким образом, количество входов у каждого нейрона выходного слоя равно m*n, что соответствует количеству коэффициентов ряда Фурье.

На рисунке 2 представлена схема отдельного нейрона скрытого слоя.

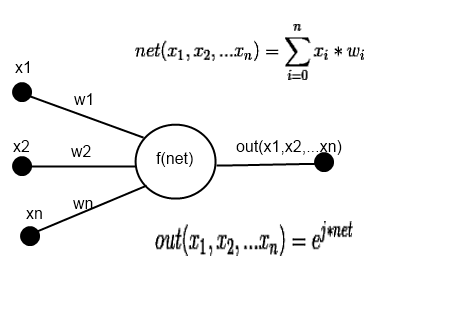
Рисунок 2. Схема нейрона скрытого слоя.

На рисунке 3 — схема нейрона выходного слоя.

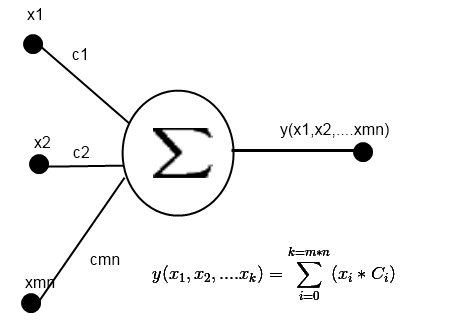Рисунок 3. Схема нейрона выходного слоя.

Оптимизация архитектуры

Создание матрицы нейронов предполагает использование больших вычислительных ресурсов. Можно сократить количество нейронов на скрытом слое в n раз. В этом случае каждый нейрон скрытого слоя имеет n выходов, если у нас в сети n входов, то при таком подходе количество связей уменьшается n квадрат раз без потери качества аппроксимации функций. Такая нейронная сеть представлена на рисунке 4.

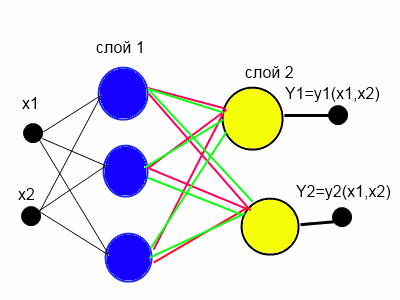Рисунок 4. КИНСФ, сведение матрицы в вектор.

Принцип работы НС

Запишем принцип работы данной НС в матричной форме.

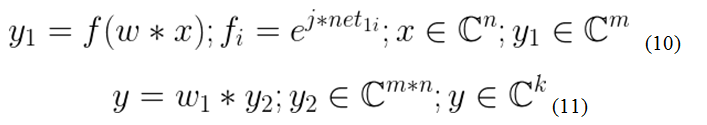Выражение 10 описывает выход скрытого слоя, где: n — размерность вектора входного «x», m — размерность выходного вектора скрытого слоя «y1», f—активационная вектор-функция, j — мнимая единица, w—матрица весов, net1=w*x, k — количество выходов НС. Выражение 11 в свою очередь показывает работу выходного слоя, вектор «y2» получен путем n-кратного дублирования вектора y1. В приложении «А», для наглядности методов реализации, представлен листинг программы, которая работает на основе выражений 10-11.

Сведение задачи обучения, к задаче обучения однослойного персептрона.

Используя физический смысл весов нейронов скрытого слоя, а именно что веса нейронов скрытого слоя представляет собой частоты. Предположив что колебания периодические можно определить начальные циклические частоты для каждого направления, и проинициализировать веса таким образом, что переходя от нейрона к нейрону частоты будут кратно увеличиваться. Так можно свести задачу обучения сложной двухслойной сети к задаче обучения однослойного персептрона. Единственная сложность заключается в том, что входы и выходы этого персептрона является комплексными. Но методы обучения данной сети мы рассмотрим в следующей статье.

Модификация КИНСФ для задач распознавания

В задачах распознавания или классификации на выходе нейронные сети необходимо получить, так называемую функцию принадлежности[3], значение которой лежит в пределах, от нуля до единицы. Для ее получения очень удобно использовать логистическую сигмоидальную функцию(Рисунок 5). преобразовав немного нейроны моей сети, возможно получить сеть для распознавания образов. Такая сеть хорошо подходит для распознавания бинарных изображений, обработанных по методу, который указан выше(выражения 1—6). Она принимает на вход комплексные числа, после чего аппроксимирует функцию принадлежности образа к классу.[4]
На рисунке 6 изображен нейрон скрытого слоя, а на рисунке 7 — выходного.

Как мы видим, схема скрытого нейрона не изменилась, чего нельзя сказать о нейронах выходного слоя.

Рисунок 6. Схема скрытого нейрона.

Рисунок 7. Схема выходного нейрона.

Эксперимент

Для эксперимента был выбран ряд картинок, одна из них представлена ниже. Перед распознаванием использовались алгоритмы бинаризация и приведения к общему виду.

Приведение к общему виду выполнялось по алгоритму, представленному выше(1-6). После чего вектор, в случае с КИНСФ подавался полностью «как есть» на искусственную нейронную сеть, а в случае с НС с сигмаидальной активационной функцией, отдельно подавались реальные и мнимые компоненты, после чего вектор распознавался. Эксперимент проводился с использованием двух типов НС. Сеть прямого распространения с сигмоидальной активационной функцией и КИНСФ. Объем обучающей выборки составил 660 векторов разбитых на 33 класса. Программа представлена на рисунке 8.

Рисунок 8. Программа для распознавания рукописного текста.

На сеть с сигмоидальной активационной функцией подаются отдельно реальные и мнимые составляющие комплексного вектора. КИНСФ и ИНС с сигмоидальной активационной функцией обучались с помощью дельта-правила 500 циклов обучения. В результате тестирования 400 изображений КИНСФ выдал точность в 87%, а ИНС с сигмоидальной активационной функцией 73%.

Код

      public class KINSF_Simple     {         ComplexVector input; // Вход         ComplexVector output, //Выход                          fOut; //Выход скрытого слоя         Matrix fL; // Матрица весов первого слоя         ComplexMatrix C; // Матрица весов второго слоя         int inpN, outpN, hN, n =0 ;         Complex J = new Complex(0,1); // Мнимая единица                           public KINSF_Simple(int inpCout, int outpCout, int hLCount)         {             inpN = inpCout;             outpN = outpCout;             hN = hLCount;             // Инициализация весов случ. образом              fL = Statistic.rand(inpN, hN);             C = Statistic.randComplex(inpN*hN,outpN);         }                                    /// <summary>         /// Вектор-функция активации первого слоя         /// </summary>         /// <param name="compVect">Вход</param>         /// <returns></returns>         public ComplexVector FActiv1(ComplexVector compVect)         {             ComplexVector outp = compVect.Copy();             for(int i = 0; i<outp.N; i++)             {                 outp.Vecktor[i] = Complex.Exp(J*outp.Vecktor[i]);             }             return outp;         }                                    /// <summary>         /// Выход первого слоя         /// </summary>         /// <param name="inp">Вход</param>         void OutputFirstLayer(ComplexVector inp)         {             input = inp;             fOut = FActiv1(inp*fL);         }                           /// <summary>         /// Выход второго слоя         /// </summary>         void OutputOutLayer()         {                 List<Complex> outList = new List<Complex>();                 for(int i = 0; i<inpN; i++)                 {                     outList.AddRange(fOut.Vecktor);                 }                 ComplexVector outVector = new ComplexVector(outList.ToArray());                                  output = fOut*C;         }                                    /// <summary>         /// Отклик НС на входной вектор         /// </summary>         /// <param name="inp">Входной вектор</param>         /// <returns></returns>         public ComplexVector NetworkOut(ComplexVector inp)         {             OutputFirstLayer(inp);             OutputOutLayer();             return output;         } } 

Видео работы

Ниже приведено видео работы данной программы, что была в тесте. Записывал его как демонстрацию того, как можно применять ИНС. Сразу извиняюсь за вольное изложение.

Итоги

Преимущества:

Данная сеть имеет ряд преимуществ. Важнейшим является то, что эта сеть может работать с комплексными числами. Ее можно использовать для работы с сигналами, заданными в комплексном виде. Также она очень хорошо подойдет для распознавания бинарных изображений. Она может аппроксимировать функцию, оставляя все свойства преобразования Фурье, что делает ее работу легко анализируемой. Ведь именно не анализируемость работы нейронных сетей приводит к тому, что научных проектах от них все чаще отказываются, решая задачи другими методами. Также физический смысл весов позволит использовать эту нейронную сеть для численного разложения функции многих переменных в ряд Фурье.

Недостатки:

Существенным недостатком данной нейронной сети является наличие большого количества связей. Намного превышающего количество связей сетей прямого распространения типа персептрон.

Дальнейшее изучение:

В ходе дальнейшей работы над этой нейронной сетью планируется: разработать более совершенные методы обучения, доказать сходимость обучения, доказать отсутствие ошибки переобучения для любого количества нейронов на скрытом слое, построить рекуррентную нейронную сеть на базе КИНСФ, предназначенную для обработки речевых и прочих сигналов.