Интересные алгоритмы кластеризации, часть вторая: DBSCAN
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Искусственный интеллект
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Разработка ИИГолосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
ИИ теория
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Внедрение ИИКомпьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Big data
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Работа разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2017-02-20 10:34

Углубимся ещё немного в малохоженные дебри Data Science. Сегодня в очереди на препарацию алгоритм кластеризации DBSCAN. Прошу под кат людей, которые сталкивались или собираются столкнуться с кластеризацией данных, в которых встречаются сгустки произвольной формы — сегодня ваш арсенал пополнится отличным инструментом.
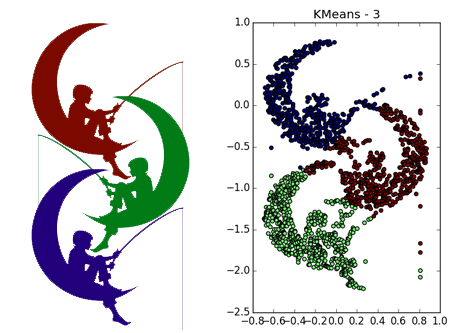 DBSCAN (Density-based spatial clustering of applications with noise, плотностной алгоритм пространственной кластеризации с присутствием шума), как следует из названия, оперирует плотностью данных. На вход он просит уже знакомую матрицу близости и два загадочных параметра — радиус -окрестности и количество соседей. Так сразу и не поймёшь, как их выбрать, причём здесь плотность, и почему именно DBSCAN хорошо расправляется с шумными данными. Без этого сложно определить границы его применимости.
DBSCAN (Density-based spatial clustering of applications with noise, плотностной алгоритм пространственной кластеризации с присутствием шума), как следует из названия, оперирует плотностью данных. На вход он просит уже знакомую матрицу близости и два загадочных параметра — радиус -окрестности и количество соседей. Так сразу и не поймёшь, как их выбрать, причём здесь плотность, и почему именно DBSCAN хорошо расправляется с шумными данными. Без этого сложно определить границы его применимости.
Давайте разберёмся. Как и в прошлой статье, предлагаю сначала обратиться к умозрительному описанию алгоритма, а затем подвести под него математику. Мне нравится объяснение, на которое я наткнулся на Quora, так что не буду изобретать велосипед, и воспроизведу его здесь с небольшими доработками.
Мы хотим разбить людей в зале на группы.
Но как выделить группы столь разной формы, да ещё и не забыть про одиночек? Попробуем оценить плотность толпы вокруг каждого человека. Наверное, если плотность толпы между двумя людьми выше определённого порога, то они принадлежат одной компании. В самом деле, будет странно, если люди, водящие «паровозик», будут относиться к разным группам, даже если плотность цепочки между ними меняется в некоторых пределах.
Будем говорить, что рядом с некоторым человеком собралась толпа, если близко к нему стоят несколько других человек. Ага, сразу видно, что нужно задать два параметра. Что значит «близко»? Возьмём какое-нибудь интуитивно понятное расстояние. Скажем, если люди могут дотронуться до голов друг друга, то они находятся близко. Около метра. Теперь, сколько именно «несколько других человек»? Допустим, три человека. Двое могут гулять и просто так, но третий — определённо лишний.
Пусть каждый подсчитает, сколько человек стоят в радиусе метра от него. Все, у кого есть хотя бы три соседа, берут в руки зелёные флажки. Теперь они коренные элементы, именно они формируют группы.
Обратимся к людям, у которых меньше трёх соседей. Выберем тех, у которых по крайней мере один соседей держит зелёный флаг, и вручим им жёлтые флаги. Скажем, что они находятся на границе групп.
Остались одиночки, у которых мало того что нет трёх соседей, так ещё и ни один из них не держит зелёный флаг. Раздадим им красные флаги. Будем считать, что они не принадлежат ни одной группе.
Таким образом, если от одного человека до другого можно создать цепочку «зелёных» людей, то эти два человека принадлежат одной группе. Очевидно, что все подобные скопища разделены либо пустым пространством либо людьми с жёлтыми флагами. Можно их пронумеровать: каждый в группе №1 может достичь по цепочке рук каждого другого в группе №1, но никого в №2, №3 и так далее. То же для остальных групп.
Если рядом с человеком с жёлтым флажком есть только один «зелёный» сосед, то он будет принадлежать той группе, к которой принадлежит его сосед. Если таких соседей несколько, и у них разные группы, то придётся выбирать. Тут можно воспользоваться разными методами — посмотреть, кто из соседей ближайший, например. Придётся как-то обходить краевые случаи, но ничего страшного.
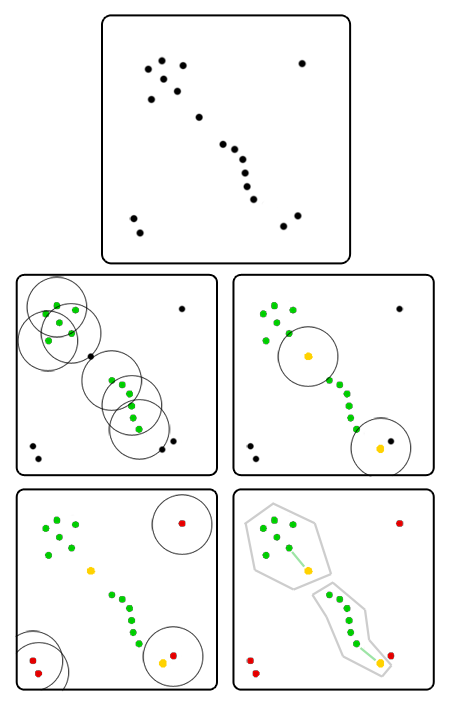 Как правило, нет смысла помечать всех коренных элементов толпы сразу. Раз от каждого коренного элемента группы можно провести цепочку до каждого другого, то всё равно с какого начинать обход — рано или поздно найдёшь всех. Тут лучше подходит итеративный вариант:
Как правило, нет смысла помечать всех коренных элементов толпы сразу. Раз от каждого коренного элемента группы можно провести цепочку до каждого другого, то всё равно с какого начинать обход — рано или поздно найдёшь всех. Тут лучше подходит итеративный вариант:
Выберем какой-нибудь корневой объект из датасета, пометим его и поместим всех его непосредственно плотно-достижимых соседей в список обхода. Теперь для каждой из списка: пометим эту точку, и, если она тоже корневая, добавим всех её соседей в список обхода. Тривиально доказывается, что кластеры помеченных точек, сформированные в ходе этого алгоритма максимальны (т.е. их нельзя расширить ещё одной точкой, чтобы удовлетворялись условия) и связны в смысле плотно-достижимости. Отсюда следует, что если мы обошли не все точки, можно перезапустить обход из какого-нибудь другого корневого объекта, и новый кластер не поглотит предыдущий.
Секундочку… Да это же замаскированный обход графа в ширину с ограничениями! Так и есть, только добавились навороты с условиями обхода и краевыми точками.
Википедия любезно предоставляет каркас псевдокода алгоритма
Или, для тех, кому псевдокод не люб, очень-очень наивная реализация на питоне
Пример более корректной реализации DBSCAN на питоне можно найти в пакете sklearn. Пример реализации в Матлабе уже был на Хабре. Если вы предпочитаете R, взгляните сюда и сюда.
DBSCAN с не-случайным правилом обработки краевых точек детерминирован. Однако большинство реализаций для ускорения работы и уменьшения количества параметров отдают краевые точки первым кластерам, которые до них дотянулись. Например, центральная жёлтая точка на картинке выше в разных запусках может принадлежать как нижнему, так и верхнему кластеру. Как правило, это несильно влияет на качество работы алгоритма, ведь через граничные точки кластер всё равно не распространяется дальше — ситуация, когда точка перескакивает из кластера в кластер и «открывает дорогу» к другим точкам, невозможна.
DBSCAN не вычисляет самостоятельно центры кластеров, однако вряд ли это проблема, особенно учитывая произвольную форму кластеров. Зато DBSCAN автоматически определяет выбросы, что довольно здорово.
Соотношение , где — размерность пространства, можно интуитивно рассматривать как пороговую плотность точек данных в области пространства. Ожидаемо, что при одинаковом соотношении , и результаты будут примерно одинаковы. Иногда это действительно так, но есть причина, почему алгоритму нужно задать два параметра, а не один. Во-первых типичное расстояние между точками в разных датасетах разное — явно задавать радиус приходится всегда. Во-вторых, играют роль неоднородности датасета. Чем больше и , тем больше алгоритм склонен «прощать» вариации плотности в кластерах. С одной стороны, это может быть полезно: неприятно увидеть в кластере «дырки», где просто не хватило данных. С другой стороны, это вредно, когда между кластерами нет чёткой границы или шум создаёт «мост» между скоплениями. Тогда DBSCAN запросто соединит две разные группы. В балансе этих параметров и кроется сложность применения DBSCAN: реальные наборы данных содержат кластеры разной плотности с границами разной степени размытости. В условиях, когда плотность некоторых границ между кластерами больше или равна плотности каких-то обособленных кластеров, приходится чем-то жертвовать.
Существуют варианты DBSCAN, способные смягчить эту проблему. Идея состоит в подстраивании в разных областях по ходу работы алгоритма. К сожалению, возрастает количество параметров алгоритма.
Существуют эвристики для выбора и . Чаще всего применяется такой метод и его вариации:
Чтобы получить чуть лучшее интуитивное представление о и , можно поиграться с параметрами онлайн здесь. Выберите DBSCAN Rings и подёргайте ползунки.
В любом случае, главные недостатки DBSCAN — неспособность соединять кластеры через проёмы, и, наоборот, способность связывать явно различные кластеры через плотно населённые перемычки. Отчасти поэтому при увеличении размерности данных коварный удар в спину наносит проклятие размерности: чем больше , тем больше мест, где могут случайно возникнуть проёмы или мосты. Напомню, что адекватное количество точек данных возрастает экспоненциально с увеличением .
DBSCAN хорошо поддаётся модифицированию. Здесь предлагают скрещивать DBSCAN с k-means для ускорения. В статье демонстрируются красивые графики, но мне не совсем понятно, как такой алгоритм выступает на кластерах размерности сильно меньше размерности пространства. См. также вариант скрещивания с Gaussian Mixture и беспараметрический вариант алгоритма.
DBSCAN распараллеливается, но это нетривиально сделать эффективно. Если процесс №1 обнаружил что множество — субкластер, а процесс №2, что — субкластер, и , то и можно объединить. Проблема состоит в том, чтобы вовремя заметить, что пересечение множеств не пусто, ведь постоянная синхронизация списков здорово подрывает производительность. См. эти статьи для вариантов реализации.
У DBSCAN есть история успешных применений. Например, можно отметить его использование в задачах:
На этом я бы хотел завершить вторую часть цикла. Надеюсь, статья вам была полезна, и теперь вы знаете, когда в задачах анализа данных стоит попробовать DBSCAN, а когда его применять не следует.

Давайте разберёмся. Как и в прошлой статье, предлагаю сначала обратиться к умозрительному описанию алгоритма, а затем подвести под него математику. Мне нравится объяснение, на которое я наткнулся на Quora, так что не буду изобретать велосипед, и воспроизведу его здесь с небольшими доработками.
Интуитивное объяснение
В гигантском зале толпа людей справляет чей-то день рождения. Кто-то слоняется один, но большинство — с товарищами. Некоторые компании просто толпятся гурьбой, некоторые — водят хороводы или танцуют ламбаду.Мы хотим разбить людей в зале на группы.
Но как выделить группы столь разной формы, да ещё и не забыть про одиночек? Попробуем оценить плотность толпы вокруг каждого человека. Наверное, если плотность толпы между двумя людьми выше определённого порога, то они принадлежат одной компании. В самом деле, будет странно, если люди, водящие «паровозик», будут относиться к разным группам, даже если плотность цепочки между ними меняется в некоторых пределах.
Будем говорить, что рядом с некоторым человеком собралась толпа, если близко к нему стоят несколько других человек. Ага, сразу видно, что нужно задать два параметра. Что значит «близко»? Возьмём какое-нибудь интуитивно понятное расстояние. Скажем, если люди могут дотронуться до голов друг друга, то они находятся близко. Около метра. Теперь, сколько именно «несколько других человек»? Допустим, три человека. Двое могут гулять и просто так, но третий — определённо лишний.
Пусть каждый подсчитает, сколько человек стоят в радиусе метра от него. Все, у кого есть хотя бы три соседа, берут в руки зелёные флажки. Теперь они коренные элементы, именно они формируют группы.
Обратимся к людям, у которых меньше трёх соседей. Выберем тех, у которых по крайней мере один соседей держит зелёный флаг, и вручим им жёлтые флаги. Скажем, что они находятся на границе групп.
Остались одиночки, у которых мало того что нет трёх соседей, так ещё и ни один из них не держит зелёный флаг. Раздадим им красные флаги. Будем считать, что они не принадлежат ни одной группе.
Таким образом, если от одного человека до другого можно создать цепочку «зелёных» людей, то эти два человека принадлежат одной группе. Очевидно, что все подобные скопища разделены либо пустым пространством либо людьми с жёлтыми флагами. Можно их пронумеровать: каждый в группе №1 может достичь по цепочке рук каждого другого в группе №1, но никого в №2, №3 и так далее. То же для остальных групп.
Если рядом с человеком с жёлтым флажком есть только один «зелёный» сосед, то он будет принадлежать той группе, к которой принадлежит его сосед. Если таких соседей несколько, и у них разные группы, то придётся выбирать. Тут можно воспользоваться разными методами — посмотреть, кто из соседей ближайший, например. Придётся как-то обходить краевые случаи, но ничего страшного.

- Подходим к случайному человеку из толпы.
- Если рядом с ним меньше трёх человек, переносим его в список возможных отшельников и выбираем кого-нибудь другого.
- Иначе:
- Исключаем его из списка людей, которых надо обойти.
- Вручаем этому человеку зелёный флажок и создаём новую группу, в которой он пока что единственный обитатель.
- Обходим всех его соседей. Если его сосед уже в списке потенциальных одиночек или рядом с ним мало других людей, то перед нами край толпы. Для простоты можно сразу пометить его жёлтым флагом, присоединить к группе и продолжить обход. Если сосед тоже оказывается «зелёным», то он не стартует новую группу, а присоединяется к уже созданной; кроме того мы добавляем в список обхода соседей соседа. Повторяем этот пункт, пока список обхода не окажется пуст.
- Повторяем шаги 1-3, пока так или иначе не обойдём всех людей.
- Разбираемся со списком отшельников. Если на шаге 3 мы уже раскидали всех краевых, то в нём остались только выбросы-одиночки — можно сразу закончить. Если нет, то нужно как-нибудь распределить людей, оставшихся в списке.
Формальный подход
Введём несколько определений. Пусть задана некоторая симметричная функция расстояния и константы и . Тогда- Назовём область , для которой , -окрестностью объекта .
- Корневым объектом или ядерным объектом степени называется объект, -окрестность которого содержит не менее объектов: .
- Объект непосредственно плотно-достижим из объекта , если и — корневой объект.
- Объект плотно-достижим из объекта , если , такие что непосредственно плотно-достижим из
Выберем какой-нибудь корневой объект из датасета, пометим его и поместим всех его непосредственно плотно-достижимых соседей в список обхода. Теперь для каждой из списка: пометим эту точку, и, если она тоже корневая, добавим всех её соседей в список обхода. Тривиально доказывается, что кластеры помеченных точек, сформированные в ходе этого алгоритма максимальны (т.е. их нельзя расширить ещё одной точкой, чтобы удовлетворялись условия) и связны в смысле плотно-достижимости. Отсюда следует, что если мы обошли не все точки, можно перезапустить обход из какого-нибудь другого корневого объекта, и новый кластер не поглотит предыдущий.
Секундочку… Да это же замаскированный обход графа в ширину с ограничениями! Так и есть, только добавились навороты с условиями обхода и краевыми точками.
Википедия любезно предоставляет каркас псевдокода алгоритма
Псевдокод
DBSCAN(D, eps, MinPts) { C = 0 for each point in dataset D { if is visited continue next point mark as visited NeighborPts = regionQuery( , eps) if sizeof(NeighborPts) < MinPts mark as NOISE else { C = next cluster expandCluster( , NeighborPts, C, eps, MinPts) } } } expandCluster( , NeighborPts, C, eps, MinPts) { add to cluster C for each point Q in NeighborPts { if Q is not visited { mark Q as visited QNeighborPts = regionQuery(Q, eps) if sizeof(QNeighborPts) >= MinPts NeighborPts = NeighborPts joined with QNeighborPts } if Q is not yet member of any cluster add Q to cluster C } } regionQuery( , eps) return all points within eps-neighborhood (including ) Или, для тех, кому псевдокод не люб, очень-очень наивная реализация на питоне
Python
from itertools import cycle from math import hypot from numpy import random import matplotlib.pyplot as plt def dbscan_naive( , eps, m, distance): NOISE = 0 C = 0 visited_points = set() clustered_points = set() clusters = {NOISE: []} def region_query(p): return [q for q in if distance(p, q) < eps] def expand_cluster(p, neighbours): if C not in clusters: clusters[C] = [] clusters[C].append(p) clustered_points.add(p) while neighbours: q = neighbours.pop() if q not in visited_points: visited_points.add(q) neighbourz = region_query(q) if len(neighbourz) > m: neighbours.extend(neighbourz) if q not in clustered_points: clustered_points.add(q) clusters[C].append(q) if q in clusters[NOISE]: clusters[NOISE].remove(q) for p in : if p in visited_points: continue visited_points.add(p) neighbours = region_query(p) if len(neighbours) < m: clusters[NOISE].append(p) else: C += 1 expand_cluster(p, neighbours) return clusters if __name__ == "__main__": = [(random.randn()/6, random.randn()/6) for i in range(150)] .extend([(random.randn()/4 + 2.5, random.randn()/5) for i in range(150)]) .extend([(random.randn()/5 + 1, random.randn()/2 + 1) for i in range(150)]) .extend([(i/25 - 1, + random.randn()/20 - 1) for i in range(100)]) .extend([(i/25 - 2.5, 3 - (i/50 - 2)**2 + random.randn()/20) for i in range(150)]) clusters = dbscan_naive( , 0.2, 4, lambda x, y: hypot(x[0] - y[0], x[1] - y[1])) for c, points in zip(cycle('bgrcmykgrcmykgrcmykgrcmykgrcmykgrcmyk'), clusters.values()): X = [p[0] for p in points] Y = [p[1] for p in points] plt.scatter(X, Y, c=c) plt.show() Пример более корректной реализации DBSCAN на питоне можно найти в пакете sklearn. Пример реализации в Матлабе уже был на Хабре. Если вы предпочитаете R, взгляните сюда и сюда.
Нюансы применения
В идеальном случае DBSCAN может достичь сложности , но не стоит особо на это рассчитывать. Если не пересчитывать каждый раз точек, то ожидаемая сложность — . Худший случай (плохие данные или брутфорс-реализация) — . Наивные реализации DBSCAN любят отъедать памяти под матрицу расстояний — это явно избыточно. Многие версии алгоритма умеют работать и с более щадящими структурами данных: sklearn и R реализации можно оптимизировать при помощи KD-tree прямо из коробки. К сожалению, из-за багов это работает не всегда.DBSCAN с не-случайным правилом обработки краевых точек детерминирован. Однако большинство реализаций для ускорения работы и уменьшения количества параметров отдают краевые точки первым кластерам, которые до них дотянулись. Например, центральная жёлтая точка на картинке выше в разных запусках может принадлежать как нижнему, так и верхнему кластеру. Как правило, это несильно влияет на качество работы алгоритма, ведь через граничные точки кластер всё равно не распространяется дальше — ситуация, когда точка перескакивает из кластера в кластер и «открывает дорогу» к другим точкам, невозможна.
DBSCAN не вычисляет самостоятельно центры кластеров, однако вряд ли это проблема, особенно учитывая произвольную форму кластеров. Зато DBSCAN автоматически определяет выбросы, что довольно здорово.
Соотношение , где — размерность пространства, можно интуитивно рассматривать как пороговую плотность точек данных в области пространства. Ожидаемо, что при одинаковом соотношении , и результаты будут примерно одинаковы. Иногда это действительно так, но есть причина, почему алгоритму нужно задать два параметра, а не один. Во-первых типичное расстояние между точками в разных датасетах разное — явно задавать радиус приходится всегда. Во-вторых, играют роль неоднородности датасета. Чем больше и , тем больше алгоритм склонен «прощать» вариации плотности в кластерах. С одной стороны, это может быть полезно: неприятно увидеть в кластере «дырки», где просто не хватило данных. С другой стороны, это вредно, когда между кластерами нет чёткой границы или шум создаёт «мост» между скоплениями. Тогда DBSCAN запросто соединит две разные группы. В балансе этих параметров и кроется сложность применения DBSCAN: реальные наборы данных содержат кластеры разной плотности с границами разной степени размытости. В условиях, когда плотность некоторых границ между кластерами больше или равна плотности каких-то обособленных кластеров, приходится чем-то жертвовать.
Существуют варианты DBSCAN, способные смягчить эту проблему. Идея состоит в подстраивании в разных областях по ходу работы алгоритма. К сожалению, возрастает количество параметров алгоритма.
Существуют эвристики для выбора и . Чаще всего применяется такой метод и его вариации:
- Выберите . Обычно используются значения от 3 до 9, чем более неоднородный ожидается датасет, и чем больше уровень шума, тем большим следует взять .
- Вычислите среднее расстояние по ближайшим соседям для каждой точки. Т.е. если , нужно выбрать трёх ближайших соседей, сложить расстояния до них и поделить на три.
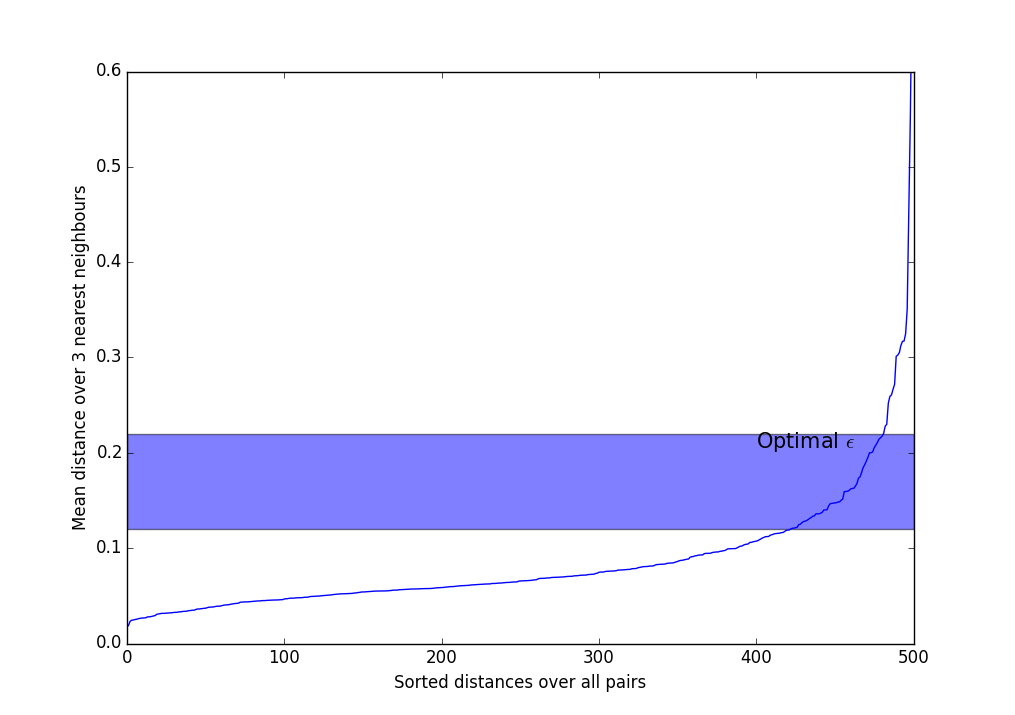
- Сортируем полученные значения по возрастанию и выводим на экран.
- Видим что-то вроде такого резко возрастающего графика. Следует взять где-нибудь в полосе, где происходит самый сильный перегиб. Чем больше , тем больше получатся кластеры, и тем меньше их будет.

Чтобы получить чуть лучшее интуитивное представление о и , можно поиграться с параметрами онлайн здесь. Выберите DBSCAN Rings и подёргайте ползунки.
В любом случае, главные недостатки DBSCAN — неспособность соединять кластеры через проёмы, и, наоборот, способность связывать явно различные кластеры через плотно населённые перемычки. Отчасти поэтому при увеличении размерности данных коварный удар в спину наносит проклятие размерности: чем больше , тем больше мест, где могут случайно возникнуть проёмы или мосты. Напомню, что адекватное количество точек данных возрастает экспоненциально с увеличением .
DBSCAN хорошо поддаётся модифицированию. Здесь предлагают скрещивать DBSCAN с k-means для ускорения. В статье демонстрируются красивые графики, но мне не совсем понятно, как такой алгоритм выступает на кластерах размерности сильно меньше размерности пространства. См. также вариант скрещивания с Gaussian Mixture и беспараметрический вариант алгоритма.
DBSCAN распараллеливается, но это нетривиально сделать эффективно. Если процесс №1 обнаружил что множество — субкластер, а процесс №2, что — субкластер, и , то и можно объединить. Проблема состоит в том, чтобы вовремя заметить, что пересечение множеств не пусто, ведь постоянная синхронизация списков здорово подрывает производительность. См. эти статьи для вариантов реализации.
Эксперименты
Don't open, pictures inside
Разбиение тех же данных при помощи k-means и Affinity propagation, см. в моём предыдущем посте.
DBSCAN отлично работает на плотных, хорошо отделённых друг от друга кластерах. При этом их форма совершенно не важна. Пожалуй, DBSCAN лучше всех неспециализированных алгоритмов обнаруживает кластеры малой размерности.


 Обратите внимание, что в примере с четырьмя прямыми в зависимости от параметров можно получить как 8 так и 4 кластера из-за разрывов в прямых. Вообще, часто это желательное поведение — неизвестно, правда ли распределение такое или у нас просто не хватает данных. Тут нам повезло: расстояние между прямыми больше размера проёма. Также обратите внимание на то, какие точки относятся к разным кластерам в примере со спиралями. Длина спирали, отнесённая к кластеру, увеличивается с уменьшением числа соседей, т.к. ближе к центру спирали точки расположены плотнее.
Обратите внимание, что в примере с четырьмя прямыми в зависимости от параметров можно получить как 8 так и 4 кластера из-за разрывов в прямых. Вообще, часто это желательное поведение — неизвестно, правда ли распределение такое или у нас просто не хватает данных. Тут нам повезло: расстояние между прямыми больше размера проёма. Также обратите внимание на то, какие точки относятся к разным кластерам в примере со спиралями. Длина спирали, отнесённая к кластеру, увеличивается с уменьшением числа соседей, т.к. ближе к центру спирали точки расположены плотнее.
Скопления разного размера определяются неплохо…
… даже когда данные сильно зашумлены. Здесь у DBSCAN преимущество перед k-means, который запросто примет несимметрично распределённые выбросы за кластер.
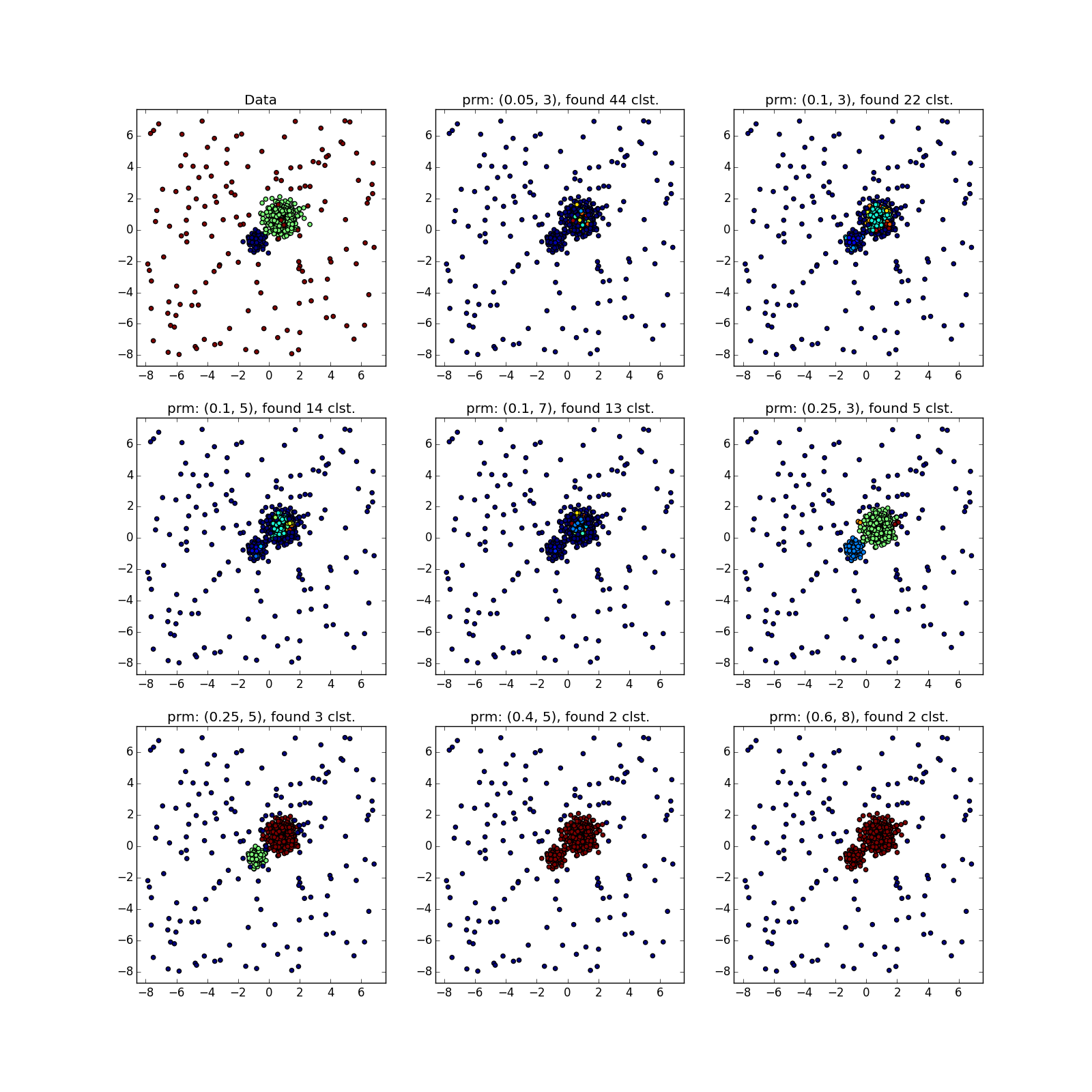
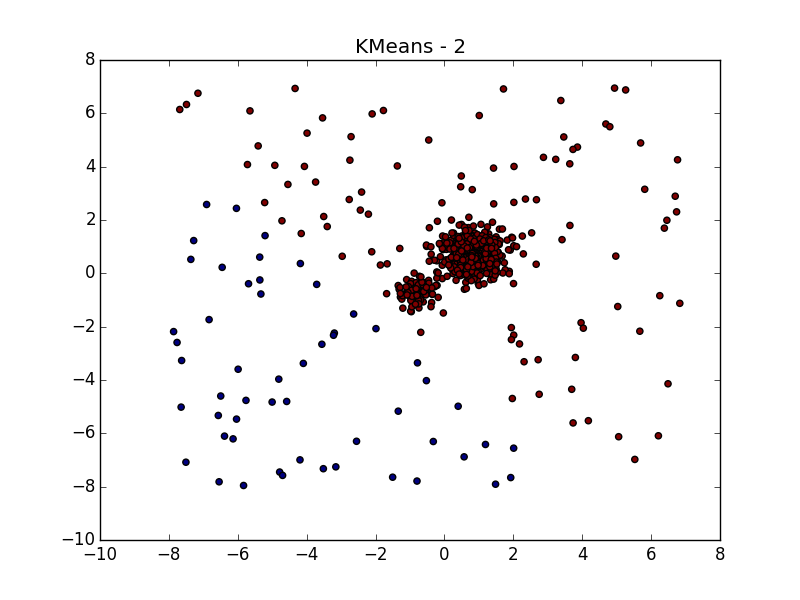 А вот со скоплениями разной плотности всё не так радужно. DBSCAN либо находит только кластер большей плотности, либо всё целиком.
А вот со скоплениями разной плотности всё не так радужно. DBSCAN либо находит только кластер большей плотности, либо всё целиком.
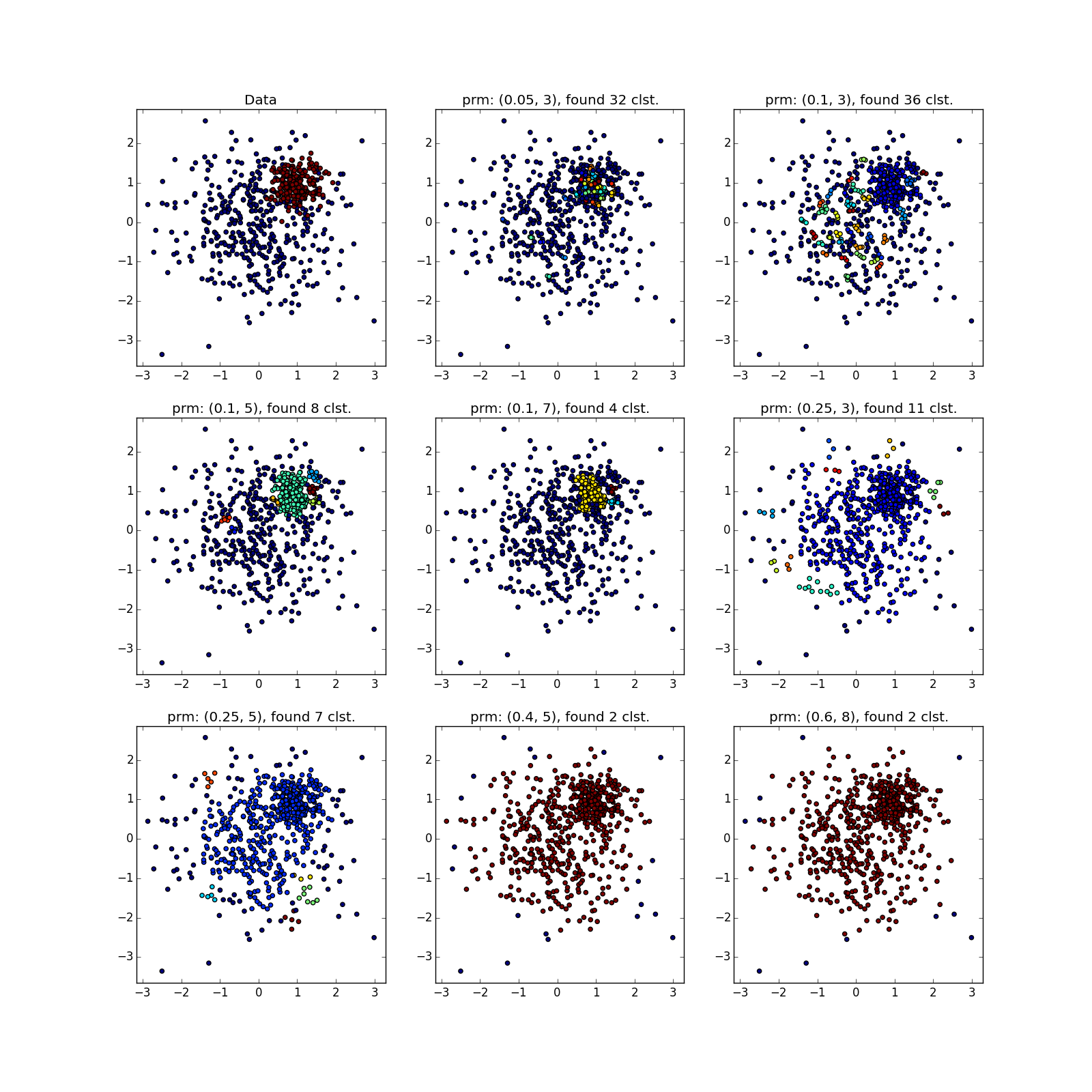
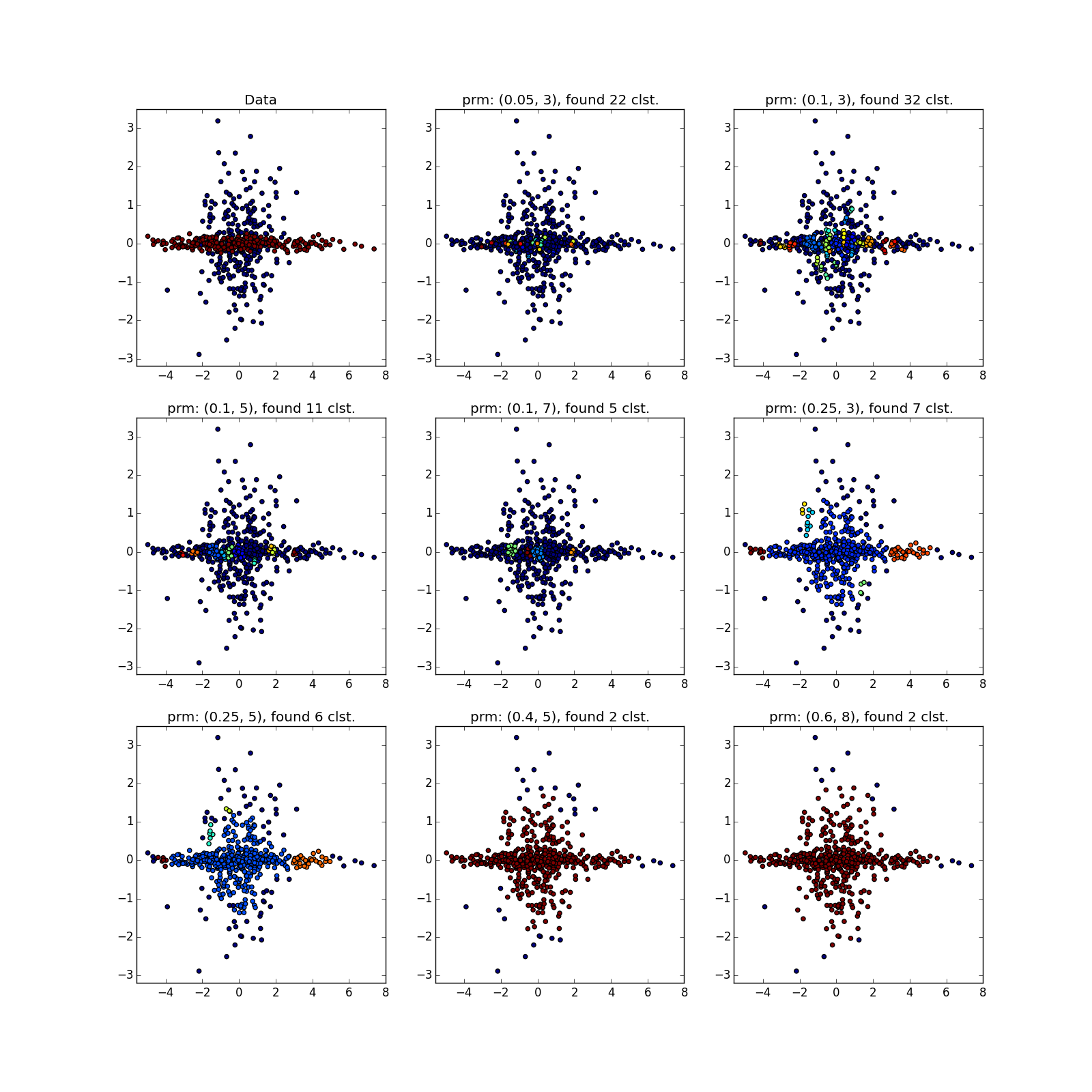
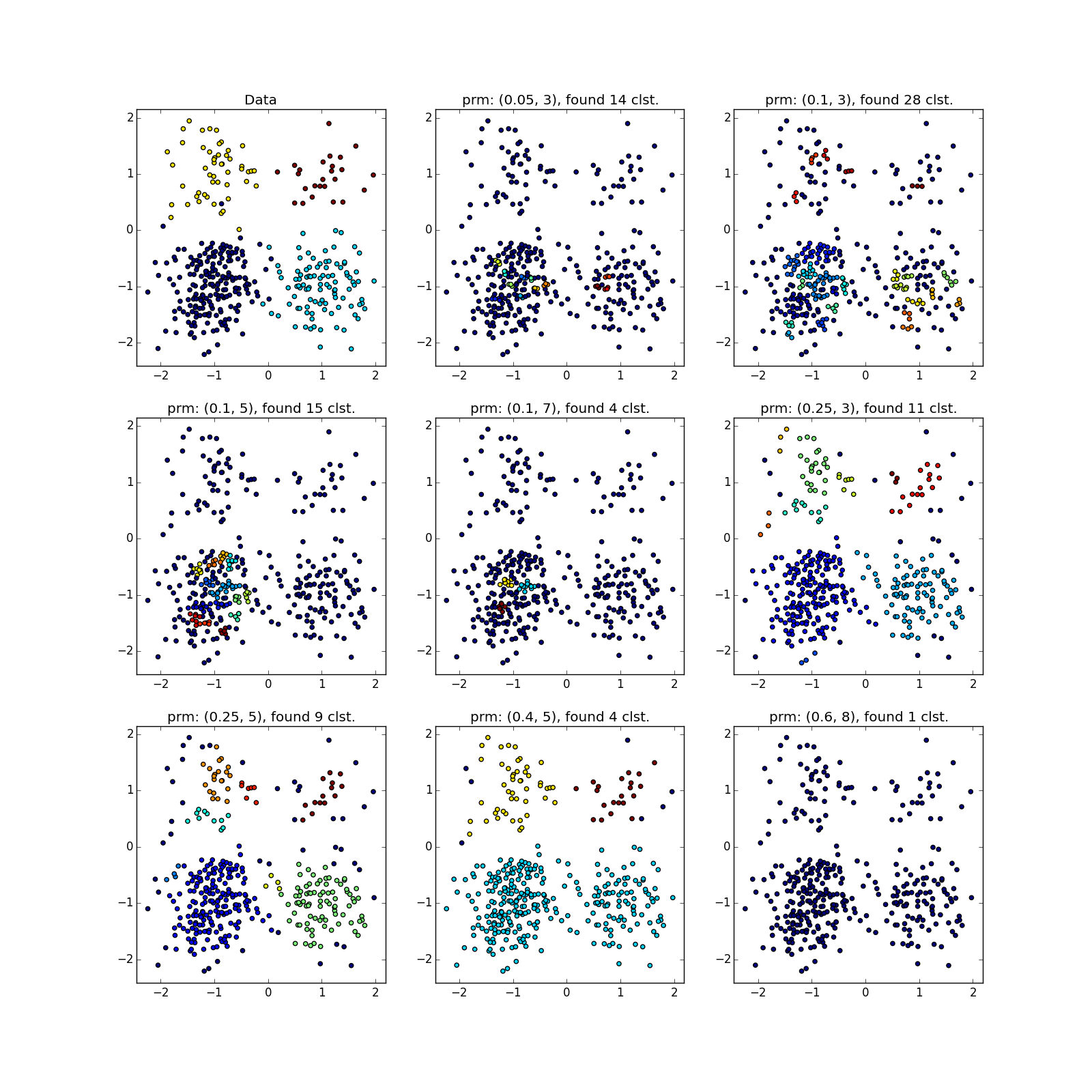 Увидеть что-то подозрительное можно разве что по счастливой случайности, либо прогнав DBSCAN несколько раз с разными параметрами. По сути — ручное исполнение разновидностей алгоритма, про которые я упоминал выше.
Увидеть что-то подозрительное можно разве что по счастливой случайности, либо прогнав DBSCAN несколько раз с разными параметрами. По сути — ручное исполнение разновидностей алгоритма, про которые я упоминал выше.
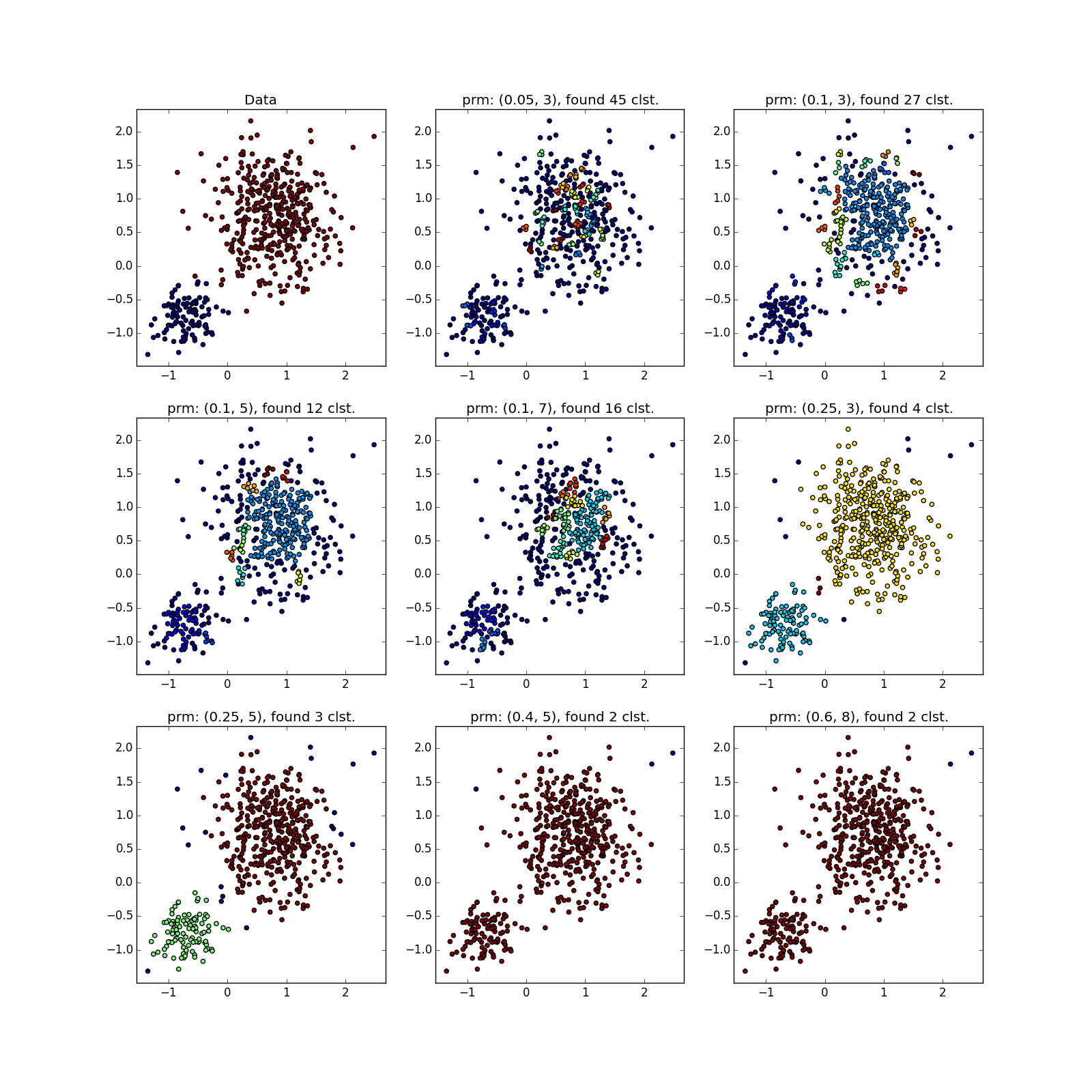
С более сложными распределениями — как повезёт. Если они хорошо отделимы друг от друга, DBSCAN работает. См. (0.4, 5) — отличное разбиение, хотя многовато точек, которые алгоритм посчитал выбросами.

Если преобладают перемычки, то не очень. В выделенных местах скопилось много точек, из-за которых DBSCAN не может различить «лепестки» явно различных распределений.
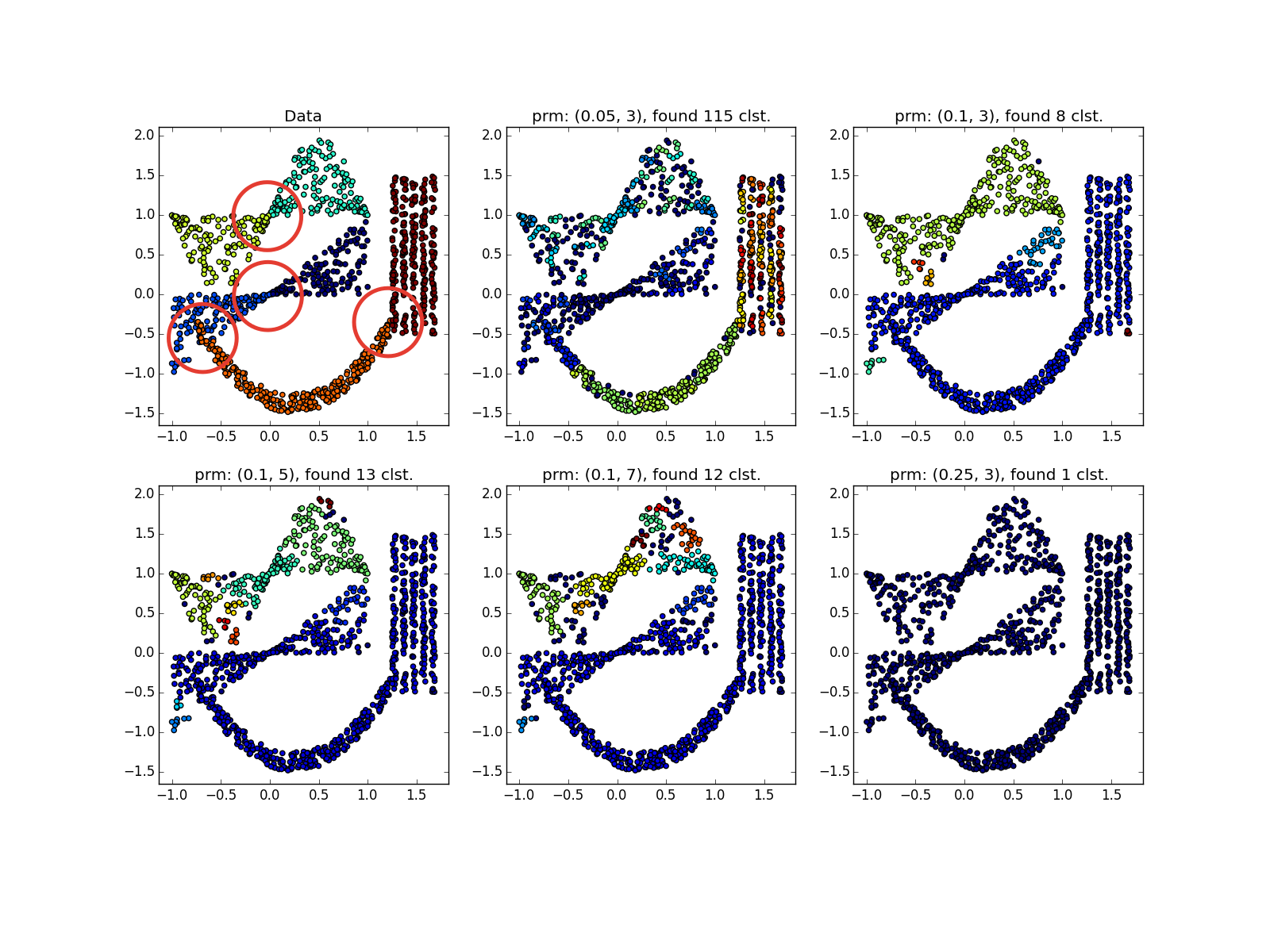
DBSCAN отлично работает на плотных, хорошо отделённых друг от друга кластерах. При этом их форма совершенно не важна. Пожалуй, DBSCAN лучше всех неспециализированных алгоритмов обнаруживает кластеры малой размерности.


 Обратите внимание, что в примере с четырьмя прямыми в зависимости от параметров можно получить как 8 так и 4 кластера из-за разрывов в прямых. Вообще, часто это желательное поведение — неизвестно, правда ли распределение такое или у нас просто не хватает данных. Тут нам повезло: расстояние между прямыми больше размера проёма. Также обратите внимание на то, какие точки относятся к разным кластерам в примере со спиралями. Длина спирали, отнесённая к кластеру, увеличивается с уменьшением числа соседей, т.к. ближе к центру спирали точки расположены плотнее.
Обратите внимание, что в примере с четырьмя прямыми в зависимости от параметров можно получить как 8 так и 4 кластера из-за разрывов в прямых. Вообще, часто это желательное поведение — неизвестно, правда ли распределение такое или у нас просто не хватает данных. Тут нам повезло: расстояние между прямыми больше размера проёма. Также обратите внимание на то, какие точки относятся к разным кластерам в примере со спиралями. Длина спирали, отнесённая к кластеру, увеличивается с уменьшением числа соседей, т.к. ближе к центру спирали точки расположены плотнее.Скопления разного размера определяются неплохо…

… даже когда данные сильно зашумлены. Здесь у DBSCAN преимущество перед k-means, который запросто примет несимметрично распределённые выбросы за кластер.

 А вот со скоплениями разной плотности всё не так радужно. DBSCAN либо находит только кластер большей плотности, либо всё целиком.
А вот со скоплениями разной плотности всё не так радужно. DBSCAN либо находит только кластер большей плотности, либо всё целиком.

 Увидеть что-то подозрительное можно разве что по счастливой случайности, либо прогнав DBSCAN несколько раз с разными параметрами. По сути — ручное исполнение разновидностей алгоритма, про которые я упоминал выше.
Увидеть что-то подозрительное можно разве что по счастливой случайности, либо прогнав DBSCAN несколько раз с разными параметрами. По сути — ручное исполнение разновидностей алгоритма, про которые я упоминал выше. С более сложными распределениями — как повезёт. Если они хорошо отделимы друг от друга, DBSCAN работает. См. (0.4, 5) — отличное разбиение, хотя многовато точек, которые алгоритм посчитал выбросами.

Если преобладают перемычки, то не очень. В выделенных местах скопилось много точек, из-за которых DBSCAN не может различить «лепестки» явно различных распределений.

Итог
Используйте DBSCAN, когда:- У вас в меру большой () датасет. Даже если под рукой оптимизированная и распаралленная реализация.
- Заранее известна функция близости, симметричная, желательно, не очень сложная. KD-Tree оптимизация часто работает только с евклидовым расстоянием.
- Вы ожидаете увидеть сгустки данных экзотической формы: вложенные и аномальные кластеры, складки малой размерности.
- Плотность границ между сгустками меньше плотности наименее плотного кластера. Лучше если кластеры вовсе отделены друг от друга.
- Сложность элементов датасета значения не имеет. Однако их должно быть достаточно, чтобы не возникало сильных разрывов в плотности (см. предыдущий пункт).
- Количество элементов в кластере может варьироваться сколь угодно.
- Количество выбросов значения не имеет (в разумных пределах), если они рассеяны по большому объёму.
- Количество кластеров значения не имеет.
У DBSCAN есть история успешных применений. Например, можно отметить его использование в задачах:
- Обнаружения социальных кружков
- Сегментирования изображений
- Моделирования поведения пользователей веб-сайтов
- Предварительная обработка в задаче предсказания погоды
На этом я бы хотел завершить вторую часть цикла. Надеюсь, статья вам была полезна, и теперь вы знаете, когда в задачах анализа данных стоит попробовать DBSCAN, а когда его применять не следует.
Источник: habrahabr.ru