Как алгоритмы помогают нам думать

Когда известный американский математик и инженер Дэнни Хиллис учился в MIT, его сосед по общежитию имел обыкновение обращаться со своими носками странным для математика способом, о котором Хиллис рассказал в своей книге «Узор на камне».

Каждая пара немного отличалась от других, поэтому после стирки носки было не так-то просто рассортировать по отдельным парам. Для этого сосед использовал следующую тактику: он вытаскивал первый попавшийся носок из кучи чистого белья, затем вынимал следующий и сравнивал с первым. Если носки совпадали, он откладывал получившуюся пару в сторону. Если не совпадали, то отправлял второй носок обратно в кучу и доставал из неё следующий. Этот процесс, как можно догадаться, занимал у него порядочное количество времени.

Однажды, в очередной раз появившись в комнате с корзиной свежевыстиранной одежды, сосед заявил, что теперь для сортировки носков он будет использовать более эффективный алгоритм. И действительно, вся процедура значительно изменилась. Как и прежде, он доставал первый носок из кучи, затем сравнивал с ним второй, но в случае несовпадения уже не возвращал его к остальному белью, а укладывал рядом.

В результате перед ним постепенно вырастал ряд носков, для каждого из которых вскоре обнаруживалась подходящая пара. Естественно, теперь это требовало гораздо меньше времени. Как ехидно замечает Хиллис, теперь родители его соседа, отличисляющие приличные деньги на учёбу в MIT, могли бы гордиться своим сыном.

Именно правильные алгоритмы могут помочь нам сохранить нужный баланс между порядком и хаосом, между тщательной регламентацией и спонтанным выбором.

Слово «алгоритм» происходит от имени персидского учёного IX века Аль-Хорезми, математические сочинения которого пользовались большим уважением в Средневековой Европе.

Источник: academic.ru

Когда речь идёт об алгоритмах, мы в первую очередь вспоминаем математику и компьютерное программирование. Но это понятие совсем не обязательно должно быть связано со сложными техническими проблемами. Алгоритм — это всего лишь последовательность действий, необходимая для достижения нужного результата. Поэтому алгоритмы объединяют и компьютерные вычислительные процессы, и человеческое поведение.

Мы склонны воспринимать компьютеры как бездушные механизмы, но на самом деле у них есть чему поучиться. И для этого совсем необязательно втискивать сложный мир человеческих эмоций и социального поведения в строгую последовательность вычислений. Алгоритмы умеют обращаться со случаем и неопределённостью даже лучше нас самих.

Правильные алгоритмы могут помочь нам принимать верные решения в условиях неопределённости, недостатка времени или ресурсов. Подумайте, например, о том, как вы выбираете новую квартиру. Вы осматриваете доступные варианты, оцениваете их качества и в какой-то момент принимаете решение: эта квартира вам подходит, больше смотреть не нужно. Но когда лучше всего остановиться? Обычно мы делаем это интуитивно. Математика же предлагает точное решение: лучше всего остановиться, просмотрев 37% доступных вариантов.

Это решение восходит к известной «дилемме секретаря». Представьте, что вам нужно нанять секретаря на новую должность. Кандидаты приходят к вам в кабинет случайном порядке; вы можете сравнивать их друг с другом, но ничего не знаете о следующих. Если сразу же после собеседования вы не приглашаете кандидата на работу, вы его теряете: он уйдёт и больше не вернётся.

Если у вас есть только два кандидата, можно выбрать кого угодно — шанс нанять лучшего всё равно будет 50/50. А вот если появляется третий, то у нас уже есть выбор. Если довериться случаю, то шанс нанять лучшего кандидата будет составлять 33,33%. Если же пропустить первого кандидата, можно нанять второго — в том случае, если он будет лучше первого — или третьего, если не будет. В таком случае вероятность оптимального решения вновь составит 50%.

А что получится, если увеличить количество кандидатов до ста? В таком случае лучше всего будет провести 37 собеседований, а затем выбрать первого, кто будет лучше всех предыдущих. Но главная прелесть этой формулы в том, что она работает при любых пропорциях: смело пропускайте первые 37% возможных вариантов, сколько бы их ни было, а затем остановитесь сразу же, как увидите кого-то получше всех предыдущих.

«Проблема секретаря» получила известность после публикации очередной колонки математика Мартина Гарднера в Scientific American.

Источник: theguardian.com

Правило тридцати семи процентов появилось в рамках теории оптимальной остановки, которая, в свою очередь, была основана на теории вероятности. Точку оптимальной остановки можно вывести с помощью сложных математических формул, но это правило работает и без них. С математической точки зрения это действительно оптимальное решение проблем вроде дилеммы секретаря. Даже в этом случае шанс найти лучшего кандидата будет составлять лишь 37%, но по сравнению с другими вариантами это очень и очень неплохо.

Не напоминает ли процесс поиска секретаря в этой задачке другие решения, которые нам приходится принимать в своей жизни? При поиске брачного партнёра тоже можно использовать правило тридцати семи процентов. По крайней мере, так попытался сделать математик Майкл Трик из университета Карнеги — Меллон.

Для начала он определил период времени, в который решение задачи должно быть найдено: а именно в возрасте от 18 до 40 лет. Получилось так, что ему в этот момент было как раз 26,1 лет — период, который как раз приходился на границу, определяемую в 37%. Следовательно, он должен был жениться на первой же встретившейся девушке, которая показалась бы ему лучше предыдущих. Когда он её встретил и действительно сделал предложение, то получил в ответ отказ.

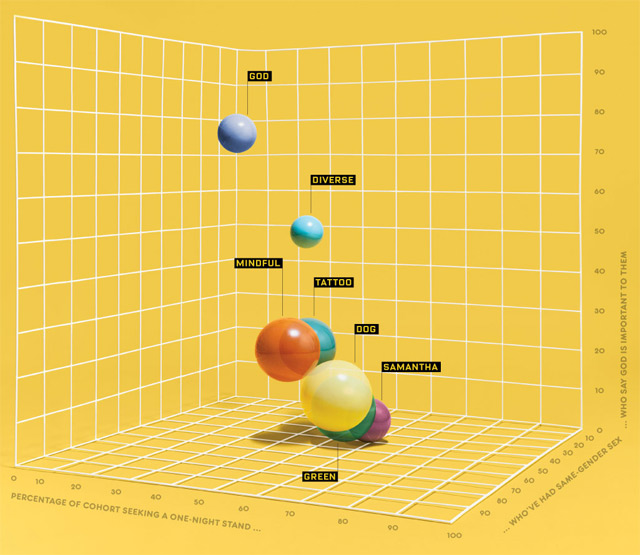
Ещё один известный случай алгоритмических поисков любви — история Криса Маккинли из Калифорнийского университета. В 2012 году тридцатипятилетний математик работал над диссертацией по анализу больших массивов данных, а заодно решил провести разведку данных на сайте знакомств OkCupid. Сервис отличается от многих других хитрой системой ранжирования: он сопоставляет друг с другом ответы пользователей на большой список вопросов и вычисляет ваш фактор совместимости.

Заполнив анкету, Маккинли нашёл около 100 девушек, у которых этот фактор превышал 90%. Но на свиданиях всё как-то не складывалось, поэтому математик решил использовать другой метод. Он создал 12 фейковых профилей и ответил на все предложенные вопросы случайным образом. В результате он получил полный доступ к анкетам всех девушек: ответив на конкретный вопрос, можно увидеть, что ответил на него тот человек, анкету которого ты просматриваешь.

Собрав около 20 тыс. анкет, он пропустил их через систему фильтров, а затем отсортировал с помощью специального скрипта по таким критериям как «Заботливые», «Верующие», «Татуировки» и т.п. После ещё целой серии дополнительных действий он создал две анкеты, заполнив их уже целенаправленно, и получил гораздо больше результатов с высокой совместимостью. Когда наступило время свиданий, ему понадобилось всего 88 попыток, чтобы отыскать действительно родственную душу.

Семь основных категорий из списка Маккинли.

Источник: habrahabr.ru

Правильные алгоритмы могут помочь нам найти баланс между новизной и старым добрым постоянством. Если вы хотите хорошо пообедать, что лучше предпочесть — любимое кафе, которое вы давно знаете, или новое место, которое открылось где-то за углом? Ведь вполне возможно, что там вам понравится ещё больше, просто вы этого пока не знаете.

Это похоже на так называемую «проблему многорукого бандита». Представьте себе множество игральных автоматов, причём на каждом из них шансы выиграть отличаются. Сколько раз вы будете переходить от одного автомата к другому, прежде чем остановиться на каком-то одном? Ответ будет сильно зависеть от того, сколько времени вы собираетесь провести в казино. Если у вас есть пять минут, лучше остановится у первого автомата, который будет приносить верную прибыль.

Чтобы разрешить дилемму старого и нового, ваш алгоритм должен свести к минимуму сожаление, которое вы испытаете, остановившись на надёжном и проверенном и не попробовав чего-то ещё. Когда Джефф Безос принял рискованное решение об основании Amazon, он открыл для себя то, что позднее назвал «принципом минимизации сожалений»:

Я представил себя 80-летним, и попытался минимизировать количество вещей, о которых я мог бы сожалеть в этом возрасте, оглядываясь на прожитую жизнь. И я понял, что в 80 лет я не буду сожалеть о своей попытке принять участие в том, что называется интернетом, который, как мне казалось, имеет огромный потенциал. Я знал, что не буду сожалеть о провале, если у меня ничего не получится, но уж точно стану расстраиваться, вспоминая, что я даже не попробовал ничего сделать. Осознание этого отказа от действий преследовало бы меня всю мою жизнь.

 

Джефф Безос

основатель Amazon.com

Дилемма старого и нового предлагает новое объяснение того, почему с возрастом люди теряют значительную часть своих социальных контактов. Может показаться, что это происходит в результате потери способностей общаться и вести активный образ жизни. Но это изменение может быть принято сознательно: люди просто перестают вкладываться в поддержание тех связей, которые мало что им дают, и сосредотачиваются на самом важном — близких друзьях и членах собственной семьи. Приближаясь к концу своей жизни, люди просто хотят остановиться на том, что обладает для них наибольшим значением.

Если казино скоро закрывается, времени для риска у вас уже нет. Вот почему поступление в колледж — приятное и волнующее событие, в отличие от переезда в дом престарелых. В обоих местах можно найти новые знакомства и получить новый опыт, но восприниматься он будет совершенно по-разному.

Казино в Лас-Вегасе можно представить как модель жизненных решений, которые нам приходится принимать постоянно.

Источник: wikipedia.org

На самом деле математика не поможет нам ответить на действительно важные вопросы, с которыми мы сталкиваемся в своей жизни: решение всегда принимаем мы сами. Но математика может предоставить ценные инструменты, с помощью которых можно посмотреть на свой опыт с другой стороны.

Во многих ситуациях мы и так действуем по алгоритмам, выписанных в нас эволюцией или культурой, — но совершенно этого не осознаём. Чем же хуже программирование собственного поведения, которое мы можем осуществить, опираясь на сознательный выбор подходящего алгоритма?

Источник: newtonew.com

Комментарии: