Кластеризация с пакетом ClusterR, часть 2
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Искусственный интеллект
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Разработка ИИГолосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
ИИ теория
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Внедрение ИИКомпьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Big data
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Работа разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2016-10-24 00:55

Эта статья посвящена кластеризации, а точнее, моему недавно добавленному в CRAN пакету ClusterR. Детали и примеры ниже в большинстве своем основаны на пакете Vignette.
Кластерный анализ или кластеризация - задача группирования набора объектов таким образом, чтобы объекты внутри одной группы (называемой кластером) были более похожи (в том или ином смысле) друг на друга, чем на объекты в других группах (кластерах). Это одна из главных задач исследовательского анализа данных и стандартная техника статистического анализа, применяемая в разных сферах, в т.ч. машинном обучении, распознавании образов, анализе изображений, поиске информации, биоинформатике, сжатии данных, компьютерной графике.
Наиболее известные примеры алгоритмов кластеризации - кластеризация на основе связности (иерархическая кластеризация), кластеризация на основе центров (метод k-средних, метод k-медоидов), кластеризация на основе распределений (GMM - Gaussian mixture models - Гауссова смесь распределений) и кластеризация на основе плотности (DBSCAN - Density-based spatial clustering of applications with noise - пространственная кластеризация приложений с шумом на основе плотности, OPTICS - Ordering points to identify the clustering structure - упорядочивание точек для определения структуры кластеризации, и др.).
В первой части: гауссова смесь распределений (GMM), метод k-средних, метод k-средних в мини-группах.
Алгоритм k-медоидов (Л. Кауфман, П. Руссо, 1987) - алгоритм кластеризации, имеющий общее с алгоритмом k-средних и алгоритмом смещения медоидов. Алогритмы k-средних и k-медоидов - разделяющие, и оба пытаются минимизировать расстояние между точками предположительно из одного кластера и точкой, назначенной центром этого кластера. В отличие от алгоритма k-средних, метод k-медоидов выбирает точки из набора данных в качестве центров (медоиды или эталоны) и работает с произвольной метрикой расстояний между точками. Полезный инструмент для определения k - ширина контура. Метод k-медоидов более устойчив к шуму и аномальным значениям, чем k-средних, поскольку он минимизирует сумму попарных отклонений, а не сумму квадратов эвклидовых расстояний. Медоид можно определить как объект кластера, чье среднее отклонение от всех остальных объектов в кластере минимально, т.е. это наиболее близкая к центру кластера точка.
Наиболее распространенная реализация кластеризации k-медоидов - алгоритм разделения вокруг медоидов (РАМ - Partitioning Around Medoids). РАМ имеет две фазы: «построить» (BUILD) и «переставить» (SWAP). На фазе BUILD алгоритм ищет хороший набор исходных медоидов, а на фазе SWAP осуществляются все возможные перемещения между BUILD-медоидами и значениями, до тех пор, пока целевая функция не перестанет убывать (Кластеризация в объектно-ориентированном окружении, А. Штруйф, М. Хуберт, П. Руссо, 1997).
В пакете ClusterR функции Cluster_Medoids и Clara_Medoids соответствуют алгоритмам PAM (partitioning around medoids) и CLARA (clustering large applications - кластеризация больших приложений).
В следующем примере кода использую данные mushroom для иллюстрации, как работает метод k-медоидов с метрикой расстояния, отличной от эвклидовой. Данные mushroom состоят из 23 категорийных атрибутов (включая класс) и 8124 значений. В документации к пакету больше информации об этих данных.
В качестве входных данных функция Cluster_Medoids может также принимать матрицу отклонений (в дополнение к матрице с данными). В случае данных mushroom, где все переменные категориальные (с двумя или более уникальными значениями), имеет смысл использовать расстояние gower. Расстояние gower применяет разные функции для разных показателей в зависимости от типа (числовой, упорядоченный и неупорядоченный список). Эта метрика отклонения реализована в ряде пакетов R, среди прочих в пакете cluster (функция daisy) и пакете FD (функция gowdis). Я воспользуюсь функцией gowdis из пакета FD, поскольку она также позволяет задать определенные пользователем веса в качестве отдельного фактора.
Как ранее упоминалось, функция gowdis пакета FD позволяет пользователю задавать разные веса для каждой отдельной переменной. Параметр weights можно подстраивать, например, с помощью случайного поиска, для достижения лучших результатов кластеризации. Например, с помощью таких весов каждой отдельной переменной можно улучшить и adjusted-rand-index (внешняя валидация), и average silhouette width (средняя ширина контура, внутренняя валидация).
CLARA (CLustering LARge Applications - кластеризация больших приложений) - очевидный выбор для кластеризации больших наборов данных. Вместо поиска медоидов для всего набора данных - расчет матрицы неподобия - также невыполнимая задача - CLARA берет небольшую выборку и применяет к ней алгоритм РАМ (Partitioning Around Medoids - разделение вокруг медоидов), чтобы сгенерировать оптимальный набор медоидов для этой выборки. Качество полученных медоидов определяется средним неподобием между каждым объектом в наборе данных и медоидом его кластера.
Функция Clara_Medoids в пакете ClusterR использует аналогичную логику, применяя функцию Cluster_Medoids к каждой выборке. Clara_Medoids принимает еще два параметра: samples и sample_size. Первый определяет количество выборок, которые нужно сформировать из исходного набора данных, второй - долю данных в каждой итерации формирования выборок (дробное число между 0.0 и 1.0). Стоит упомянуть, что функция Clara_Medoids не принимает на вход матрицу неподобия, в отличие от функции Cluster_Medoids.
Я применю функцию Clara_Medoids к ранее использованному набору данных mushroom, взяв расстояние Хемминга как метрику неподобия, и сравню время вычисления и результат с результатом функции Cluster_Medoids. Расстояние Хемминга подходит для данных mushroom, т.к. оно применимо к дискретным переменным и определяется, как количество атрибутов, принимающих разные значения для двух сравниваемых экземпляров («Алгоритмы интеллектуального анализа данных: объяснение с R», Пауэл Чикош, 2015, стр. 318).
С использованием расстояния Хемминга и Clara_Medoids, и Cluster_Medoids возвращают примерно одинаковый результат (по сравнению с результатами для расстояния gower), но при этом функция Clara_Medoids работает более чем в четыре раза быстрее, чем Cluster_Medoids, для этого набора данных.
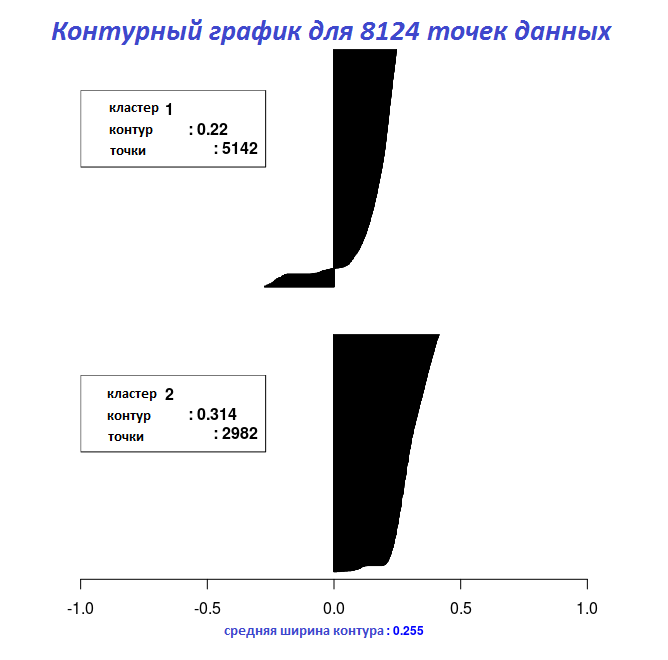
С результатами последних двух фрагментов кода можно построить на графике ширину контура с помощью функции Silhouette_Dissimilarity_Plot. Здесь стоит упомянуть, что неподобие и ширина контура в функции Clara_Medoids - на лучшей выборке, а не на всем наборе данных, как для функции Cluster_Medoids.
Реализация функций k-медоидов (Cluster_Medoids и Clara_Medoids) заняла у меня довольно много времени, поскольку вначале я думал, что начальные медоиды инициализируются так же, как и центры в алгоритме k-средних. Т.к. у меня не было доступа к книге Кауфмана и Руссо, очень помог пакет cluster с подробнейшей документацией. Он включает оба алгоритма, и РАМ (Partitioning Around Medoids - разделение вокруг медоидов), и CLARA (CLustering LARge Applications - кластеризация больших приложений), при желании можно сравнить результаты.
В следующем фрагменте кода сравню функцию pam пакета cluster и Cluster_Medoids пакета ClusterR и полученные медоиды, основываясь на предыдущем примере квантизации.
Для этого набора данных (5625 строк и 3 колонки) функция Cluster_Medoids возвращает те же медоиды почти в четыре раза быстрее, чем функция pam, если доступен OpenMP (6 потоков).
Актуальная версия пакета ClusterR доступна в моем Github репозитории, а для баг-репортов, пожалуйста, используйте эту ссылку.
Кластерный анализ или кластеризация - задача группирования набора объектов таким образом, чтобы объекты внутри одной группы (называемой кластером) были более похожи (в том или ином смысле) друг на друга, чем на объекты в других группах (кластерах). Это одна из главных задач исследовательского анализа данных и стандартная техника статистического анализа, применяемая в разных сферах, в т.ч. машинном обучении, распознавании образов, анализе изображений, поиске информации, биоинформатике, сжатии данных, компьютерной графике.
Наиболее известные примеры алгоритмов кластеризации - кластеризация на основе связности (иерархическая кластеризация), кластеризация на основе центров (метод k-средних, метод k-медоидов), кластеризация на основе распределений (GMM - Gaussian mixture models - Гауссова смесь распределений) и кластеризация на основе плотности (DBSCAN - Density-based spatial clustering of applications with noise - пространственная кластеризация приложений с шумом на основе плотности, OPTICS - Ordering points to identify the clustering structure - упорядочивание точек для определения структуры кластеризации, и др.).
В первой части: гауссова смесь распределений (GMM), метод k-средних, метод k-средних в мини-группах.
Метод k-медоидов
Алгоритм k-медоидов (Л. Кауфман, П. Руссо, 1987) - алгоритм кластеризации, имеющий общее с алгоритмом k-средних и алгоритмом смещения медоидов. Алогритмы k-средних и k-медоидов - разделяющие, и оба пытаются минимизировать расстояние между точками предположительно из одного кластера и точкой, назначенной центром этого кластера. В отличие от алгоритма k-средних, метод k-медоидов выбирает точки из набора данных в качестве центров (медоиды или эталоны) и работает с произвольной метрикой расстояний между точками. Полезный инструмент для определения k - ширина контура. Метод k-медоидов более устойчив к шуму и аномальным значениям, чем k-средних, поскольку он минимизирует сумму попарных отклонений, а не сумму квадратов эвклидовых расстояний. Медоид можно определить как объект кластера, чье среднее отклонение от всех остальных объектов в кластере минимально, т.е. это наиболее близкая к центру кластера точка.
Наиболее распространенная реализация кластеризации k-медоидов - алгоритм разделения вокруг медоидов (РАМ - Partitioning Around Medoids). РАМ имеет две фазы: «построить» (BUILD) и «переставить» (SWAP). На фазе BUILD алгоритм ищет хороший набор исходных медоидов, а на фазе SWAP осуществляются все возможные перемещения между BUILD-медоидами и значениями, до тех пор, пока целевая функция не перестанет убывать (Кластеризация в объектно-ориентированном окружении, А. Штруйф, М. Хуберт, П. Руссо, 1997).
В пакете ClusterR функции Cluster_Medoids и Clara_Medoids соответствуют алгоритмам PAM (partitioning around medoids) и CLARA (clustering large applications - кластеризация больших приложений).
В следующем примере кода использую данные mushroom для иллюстрации, как работает метод k-медоидов с метрикой расстояния, отличной от эвклидовой. Данные mushroom состоят из 23 категорийных атрибутов (включая класс) и 8124 значений. В документации к пакету больше информации об этих данных.
Cluster_Medoids
В качестве входных данных функция Cluster_Medoids может также принимать матрицу отклонений (в дополнение к матрице с данными). В случае данных mushroom, где все переменные категориальные (с двумя или более уникальными значениями), имеет смысл использовать расстояние gower. Расстояние gower применяет разные функции для разных показателей в зависимости от типа (числовой, упорядоченный и неупорядоченный список). Эта метрика отклонения реализована в ряде пакетов R, среди прочих в пакете cluster (функция daisy) и пакете FD (функция gowdis). Я воспользуюсь функцией gowdis из пакета FD, поскольку она также позволяет задать определенные пользователем веса в качестве отдельного фактора.
data(mushroom) X = mushroom[, -1] y = as.numeric(mushroom[, 1]) # конвертировать метки в числа gwd = FD::gowdis(X) # посчитать расстояние 'gower' для факторных переменных gwd_mat = as.matrix(gwd) # конвертировать расстояния в матрицу cm = Cluster_Medoids(gwd_mat, clusters = 2, swap_phase = TRUE, verbose = F) | adjusted_rand_index | avg_silhouette_width |
|---|---|
| 0.5733587 | 0.2545221 |
| predictors | weights |
|---|---|
| cap_shape | 4.626 |
| cap_surface | 38.323 |
| cap_color | 55.899 |
| bruises | 34.028 |
| odor | 169.608 |
| gill_attachment | 6.643 |
| gill_spacing | 42.08 |
| gill_size | 57.366 |
| gill_color | 37.938 |
| stalk_shape | 33.081 |
| stalk_root | 65.105 |
| stalk_surface_above_ring | 18.718 |
| stalk_surface_below_ring | 76.165 |
| stalk_color_above_ring | 27.596 |
| stalk_color_below_ring | 26.238 |
| veil_type | 0.0 |
| veil_color | 1.507 |
| ring_number | 37.314 |
| ring_type | 32.685 |
| spore_print_color | 127.87 |
| population | 64.019 |
| habitat | 44.519 |
weights = c(4.626, 38.323, 55.899, 34.028, 169.608, 6.643, 42.08, 57.366, 37.938, 33.081, 65.105, 18.718, 76.165, 27.596, 26.238, 0.0, 1.507, 37.314, 32.685, 127.87, 64.019, 44.519) gwd_w = FD::gowdis(X, w = weights) # расстояние 'gower' с применением весов d_mat_w = as.matrix(gwd_w) # преобразование расстояний в матрицу cm_w = Cluster_Medoids(gwd_mat_w, clusters = 2, swap_phase = TRUE, verbose = F) | adjusted_rand_index | avg_silhouette_width |
|---|---|
| 0.6197672 | 0.3000048 |
Clara_Medoids
CLARA (CLustering LARge Applications - кластеризация больших приложений) - очевидный выбор для кластеризации больших наборов данных. Вместо поиска медоидов для всего набора данных - расчет матрицы неподобия - также невыполнимая задача - CLARA берет небольшую выборку и применяет к ней алгоритм РАМ (Partitioning Around Medoids - разделение вокруг медоидов), чтобы сгенерировать оптимальный набор медоидов для этой выборки. Качество полученных медоидов определяется средним неподобием между каждым объектом в наборе данных и медоидом его кластера.
Функция Clara_Medoids в пакете ClusterR использует аналогичную логику, применяя функцию Cluster_Medoids к каждой выборке. Clara_Medoids принимает еще два параметра: samples и sample_size. Первый определяет количество выборок, которые нужно сформировать из исходного набора данных, второй - долю данных в каждой итерации формирования выборок (дробное число между 0.0 и 1.0). Стоит упомянуть, что функция Clara_Medoids не принимает на вход матрицу неподобия, в отличие от функции Cluster_Medoids.
Я применю функцию Clara_Medoids к ранее использованному набору данных mushroom, взяв расстояние Хемминга как метрику неподобия, и сравню время вычисления и результат с результатом функции Cluster_Medoids. Расстояние Хемминга подходит для данных mushroom, т.к. оно применимо к дискретным переменным и определяется, как количество атрибутов, принимающих разные значения для двух сравниваемых экземпляров («Алгоритмы интеллектуального анализа данных: объяснение с R», Пауэл Чикош, 2015, стр. 318).
cl_X = X # скопировать исходные данные # функция Clara_Medoids принимает только числовые атрибуты # поэтому сначала привести к числовым for (i in 1:ncol(cl_X)) { cl_X[, i] = as.numeric(cl_X[, i]) } start = Sys.time() cl_f = Clara_Medoids(cl_X, clusters = 2, distance_metric = 'hamming', samples = 5, sample_size = 0.2, swap_phase = TRUE, verbose = F, threads = 1) end = Sys.time() t = end - start cat('time to complete :', t, attributes(t)$units, ' ') # время вычисления : 3.104652 сек | adjusted_rand_index | avg_silhouette_width |
|---|---|
| 0.5944456 | 0.2678507 |
start = Sys.time() cl_e = Cluster_Medoids(cl_X, clusters = 2, distance_metric = 'hamming', swap_phase = TRUE, verbose = F, threads = 1) end = Sys.time() t = end - start cat('time to complete :', t, attributes(t)$units, ' ') # время вычисления : 14.93423 сек | adjusted_rand_index | avg_silhouette_width |
|---|---|
| 0.5733587 | 0.2545221 |
С использованием расстояния Хемминга и Clara_Medoids, и Cluster_Medoids возвращают примерно одинаковый результат (по сравнению с результатами для расстояния gower), но при этом функция Clara_Medoids работает более чем в четыре раза быстрее, чем Cluster_Medoids, для этого набора данных.
С результатами последних двух фрагментов кода можно построить на графике ширину контура с помощью функции Silhouette_Dissimilarity_Plot. Здесь стоит упомянуть, что неподобие и ширина контура в функции Clara_Medoids - на лучшей выборке, а не на всем наборе данных, как для функции Cluster_Medoids.
# Контурный график для объекта "Clara_Medoids" Silhouette_Dissimilarity_Plot(cl_f, silhouette = TRUE) # Контурный график для объекта "Cluster_Medoids" Silhouette_Dissimilarity_Plot(cl_e, silhouette = TRUE) 
Ссылки для функций k-медоидов
Реализация функций k-медоидов (Cluster_Medoids и Clara_Medoids) заняла у меня довольно много времени, поскольку вначале я думал, что начальные медоиды инициализируются так же, как и центры в алгоритме k-средних. Т.к. у меня не было доступа к книге Кауфмана и Руссо, очень помог пакет cluster с подробнейшей документацией. Он включает оба алгоритма, и РАМ (Partitioning Around Medoids - разделение вокруг медоидов), и CLARA (CLustering LARge Applications - кластеризация больших приложений), при желании можно сравнить результаты.
В следующем фрагменте кода сравню функцию pam пакета cluster и Cluster_Medoids пакета ClusterR и полученные медоиды, основываясь на предыдущем примере квантизации.
#==================================== # функция pam пакета cluster #==================================== start_pm = Sys.time() set.seed(1) pm_vq = cluster::pam(im2, k = 5, metric = 'euclidean', do.swap = TRUE) end_pm = Sys.time() t_pm = end_pm - start_pm cat('time to complete :', t_pm, attributes(t_pm)$units, ' ') # время вычисления : 12.05006 сек pm_vq$medoids # [,1] [,2] [,3] # [1,] 1.0000000 1.0000000 1.0000000 # [2,] 0.6325856 0.6210824 0.5758536 # [3,] 0.4480000 0.4467451 0.4191373 # [4,] 0.2884769 0.2884769 0.2806337 # [5,] 0.1058824 0.1058824 0.1058824 #==================================== # функция Cluster_Medoids пакета ClusterR с использованием 6 потоков (параллелизация доступна с OpenMP) #==================================== start_vq = Sys.time() set.seed(1) cl_vq = Cluster_Medoids(im2, clusters = 5, distance_metric = 'euclidean', swap_phase = TRUE, verbose = F, threads = 6) end_vq = Sys.time() t_vq = end_vq - start_vq cat('time to complete :', t_vq, attributes(t_vq)$units, ' ') # время вычисления : 3.333658 сек cl_vq$medoids # [,1] [,2] [,3] # [1,] 0.2884769 0.2884769 0.2806337 # [2,] 0.6325856 0.6210824 0.5758536 # [3,] 0.4480000 0.4467451 0.4191373 # [4,] 0.1058824 0.1058824 0.1058824 # [5,] 1.0000000 1.0000000 1.0000000 #==================================== # функция Cluster_Medoids пакета ClusterR в один поток #==================================== start_vq_single = Sys.time() set.seed(1) cl_vq_single = Cluster_Medoids(im2, clusters = 5, distance_metric = 'euclidean', swap_phase = TRUE, verbose = F, threads = 1) end_vq_single = Sys.time() t_vq_single = end_vq_single - start_vq_single cat('time to complete :', t_vq_single, attributes(t_vq_single)$units, ' ') # время вычисления : 8.693385 сек cl_vq_single$medoids # [,1] [,2] [,3] # [1,] 0.2863456 0.2854044 0.2775613 # [2,] 1.0000000 1.0000000 1.0000000 # [3,] 0.6325856 0.6210824 0.5758536 # [4,] 0.4480000 0.4467451 0.4191373 # [5,] 0.1057339 0.1057339 0.1057339 Для этого набора данных (5625 строк и 3 колонки) функция Cluster_Medoids возвращает те же медоиды почти в четыре раза быстрее, чем функция pam, если доступен OpenMP (6 потоков).
Актуальная версия пакета ClusterR доступна в моем Github репозитории, а для баг-репортов, пожалуйста, используйте эту ссылку.
Источник: habrahabr.ru