Кластеризация с пакетом ClusterR, часть 1

2016-09-26 21:30

Эта статья посвящена кластеризации, а точнее, моему недавно добавленному в CRAN пакету ClusterR. Детали и примеры ниже в большинстве своем основаны на пакете Vignette.

Кластерный анализ или кластеризация - задача группирования набора объектов таким образом, чтобы объекты внутри одной группы (называемой кластером) были более похожи (в том или ином смысле) друг на друга, чем на объекты в других группах (кластерах). Это одна из главных задач исследовательского анализа данных и стандартная техника статистического анализа, применяемая в разных сферах, в т.ч. машинном обучении, распознавании образов, анализе изображений, поиске информации, биоинформатике, сжатии данных, компьютерной графике.

Наиболее известные примеры алгоритмов кластеризации - кластеризация на основе связности (иерархическая кластеризация), кластеризация на основе центров (метод k-средних, метод k-медоидов), кластеризация на основе распределений (GMM - Gaussian mixture models - Гауссова смесь распределений) и кластеризация на основе плотности (DBSCAN - Density-based spatial clustering of applications with noise - пространственная кластеризация приложений с шумом на основе плотности, OPTICS - Ordering points to identify the clustering structure - упорядочивание точек для определения структуры кластеризации, и др.).

Пакет ClusterR состоит из алгоритмов кластеризации на основе центров (метод k-средних, k-средних в мини-группах, k-медоидов) и распределений (GMM). Также пакет предлагает функции для:

валидации выходных данных с помощью меток истинности;
вывода результатов на контурном или двумерном графике;
предсказания новых результатов наблюдений;
оценки оптимального числа кластеров для каждого отдельного алгоритма.

Гауссова смесь распределений (GMM - Gaussian mixture models)

Гауссова смесь распределений - статистическая модель для представления нормально распределенных субпопуляций внутри общей популяции. Гауссова смесь распределений параметризируется двумя типами значений - смесь весов компонентов и средних компонентов или ковариаций (для многомерного случая). Если количество компонентов известно, техника, чаще всего используемая для оценки параметров смеси распределений - ЕМ-алгоритм.

Функция GMM в пакете ClusterR - реализация на R класса для моделирования данных как гауссовой смеси распределений (GMM) из библиотеки Armadillo с предположением о диагональных ковариационных матрицах. Можно настраивать параметры функции, в том числе gaussian_comps, dist_mode (eucl_dist, maha_dist), seed_mode (static_subset, random_subset, static_spread, random_spread), km_iter и em_iter (больше информации о параметрах в документации к пакету). Проиллюстрирую функцию GMM на синтетических данных dietary_survey_IBS.

library(ClusterR) data(dietary_survey_IBS) dim(dietary_survey_IBS)

## [1] 400  43

X = dietary_survey_IBS[, -ncol(dietary_survey_IBS)]   # данные (без зависимой переменной) y = dietary_survey_IBS[, ncol(dietary_survey_IBS)]    # зависимая переменная dat = center_scale(X, mean_center = T, sd_scale = T)  # центрирование и масштабирование данных gmm = GMM(dat, 2, dist_mode = "maha_dist", seed_mode = "random_subset", km_iter = 10,           em_iter = 10, verbose = F)            # предсказание центроидов, ковариационной матрицы и весов pr = predict_GMM(dat, gmm$centroids, gmm$covariance_matrices, gmm$weights)

Исходно функция GMM возвращает центроиды, матрицу ковариации (где каждая строка представляет диагональную ковариационную матрицу), веса и логарифмические функции правдоподобия для каждой гауссовой компоненты. Затем функция predict_GMM берет выходные данные модели GMM и возвращает вероятные кластеры.

В дополнение к уже упомянутым функциям можно использовать Optimal_Clusters_GMM для оценки количества кластеров данных с помощью или информационного критерия Акаике (AIC, Akaike information), или байесовского информационного критерия (BIC, Bayesian information).

opt_gmm = Optimal_Clusters_GMM(dat, max_clusters = 10, criterion = "BIC",                                 dist_mode = "maha_dist", seed_mode = "random_subset",                                km_iter = 10, em_iter = 10, var_floor = 1e-10,                                 plot_data = T)

При выборе модели из предопределенного множества предпочтительнее выбирать ту, у которой самый низкий BIC, здесь это справедливо для количества кластеров, равного 2.

Предполагая, что доступны метки истинности, для валидации выходных кластеров можно использовать методы external_validation (rand_index, adjusted_rand_index, jaccard_index, fowlkes_Mallows_index, mirkin_metric, purity, entropy, nmi (нормализованная взаимная информация) и var_info (вариация информации).

res = external_validation(dietary_survey_IBS$class, pr$cluster_labels,                            method = "adjusted_rand_index", summary_stats = T) res

##   ## ----------------------------------------  ## purity                         : 1  ## entropy                        : 0  ## normalized mutual information  : 1  ## variation of information       : 0  ## ----------------------------------------  ## specificity                    : 1  ## sensitivity                    : 1  ## precision                      : 1  ## recall                         : 1  ## F-measure                      : 1  ## ----------------------------------------  ## accuracy OR rand-index         : 1  ## adjusted-rand-index            : 1  ## jaccard-index                  : 1  ## fowlkes-mallows-index          : 1  ## mirkin-metric                  : 0  ## ----------------------------------------

И если параметр summary_stats установлен в TRUE, то возвращаются также метрики специфичности, чувствительности, точности, полноты, F-меры (specificity, sensitivity, precision, recall, F-measure соответственно).

Метод k-средних

Кластеризация методом k-средних - метод векторного квантования, исходно применяемый в обработке сигналов, часто используется для кластерного анализа данных. Цель кластеризации методом k-средних - разделить n значений на k кластеров, в которых каждое значение принадлежит кластеру с ближайшим средним, выступающим прототипом кластера. Это приводит к разделению области данных на ячейки Вороного. Наиболее часто применяемый алгоритм использует итеративную уточняющую технику. Из-за повсеместного употребления, его называют алгоритмом k-средних; в частности, среди специалистов в сфере компьютерных наук он также известен как алгоритм Ллойда.

Пакет ClusterR предоставляет две разных функции k-средних, KMeans_arma, реализацию на R метода k-средних из библиотеки armadillo, и KMeans_rcpp, которая использует пакет RcppArmadillo. Обе функции приводят к одним и тем же результатам, однако, возвращают разные признаки (код ниже иллюстрирует это).

KMeans_arma

KMeans_arma быстрее, чем функция KMeans_rcpp, однако, исходно она выводит центроиды только некоторых кластеров. Более того, количество колонок в данных должно превышать количество кластеров, иначе функция вернет ошибку. Кластеризация будет работать быстрее на многоядерных машинах с включенным OpenMP (например, -fopenmp в GCC). Алгоритм инициализируется один раз, и обычно 10 итераций достаточно для сходимости. Исходные центроиды распределяются с помощью одного из алгоритмов - keep_existing, static_subset, random_subset, static_spread или random_spread. Если seed_mode равно keep_existing, пользователь должен передать на вход матрицу центроидов.

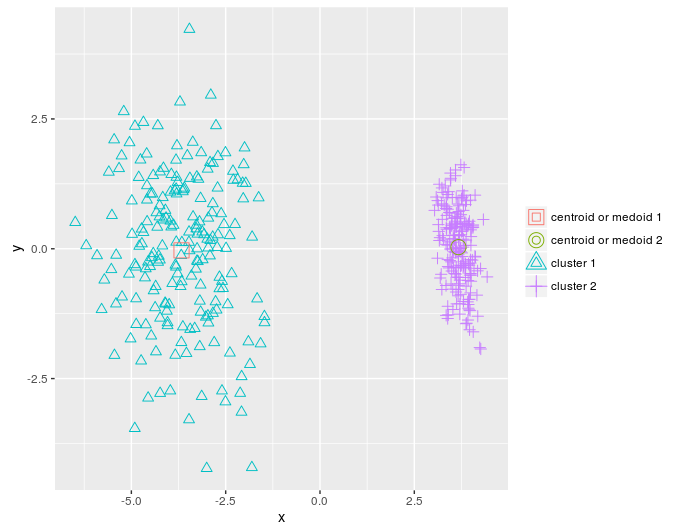
Я уменьшу количество измерений в данных dietary_survey_IBS с помощью анализа главных компонент (PCA - principal component analysis), а именно - функции princomp из пакета stats, чтобы можно было вывести двумерный график кластеров, построенных в результате.

pca_dat = stats::princomp(dat)$scores[, 1:2] km = KMeans_arma(pca_dat, clusters = 2, n_iter = 10, seed_mode = "random_subset",                   verbose = T, CENTROIDS = NULL) pr = predict_KMeans(pca_dat, km) table(dietary_survey_IBS$class, pr) class(km) = 'matrix' plot_2d(data = pca_dat, clusters = as.vector(pr), centroids_medoids = as.matrix(km))

KMeans_rcpp

Как утверждалось выше, функция KMeans_rcpp предлагает некоторые дополнительные возможности по сравнению с функцией KMeans_arma:

она позволяет более одной инициализации (можно параллелизировать с OpenMP)
помимо инициализаций с optimal_init, quantile_init, random или kmeans++, можно задать центроиды в параметре CENTROIDS
время работы алгоритма и его сходимость можно настраивать параметрами num_init, max_iters и tol
если num_init > 1, KMeans_rcpp возвращает атрибуты лучшей инициализации, используя критерий within-cluster-sum-of-squared-error (сумма-квадратов-ошибок-внутри-кластера)
алгоритм возвращает следующие атрибуты: clusters, fuzzy_clusters (если fuzzy = TRUE), centroids, total_SSE, best_initialization, WCSS_per_cluster, obs_per_cluster, between.SS_DIV_total.SS

Больше подробностей о KMeans_rcpp есть в документации пакета. Проиллюстрирую разные параметры KMeans_rcpp на примере векторного квантования и пакета OpenImageR.

library(OpenImageR) path = 'elephant.jpg' im = readImage(path)  # сначала изменим размер картинки, чтобы уменьшить количество измерений im = resizeImage(im, 75, 75, method = 'bilinear')             imageShow(im)                                                # вывод исходного изображения im2 = apply(im, 3, as.vector)                                # векторизированный RGB

# кластеризация с KMeans_rcpp km_rc = KMeans_rcpp(im2, clusters = 5, num_init = 5, max_iters = 100,                      initializer = 'optimal_init', threads = 1, verbose = F) km_rc$between.SS_DIV_total.SS

## [1] 0.9873009

Атрибут between.SS_DIV_total.SS равен (total_SSE - sum(WCSS_per_cluster)) / total_SSE. Если в кластеризации нет закономерности, промежуточная сумма квадратов будет очень небольшой частью общей суммы квадратов, а если атрибут between.SS_DIV_total.SS близок к 1.0, значения кластеризуются достаточно хорошо.

getcent = km_rc$centroids getclust = km_rc$clusters new_im = getcent[getclust, ]     # каждое значение ассоциируется с ближайшим центроидом dim(new_im) = c(nrow(im), ncol(im), 3)        # обратное преобразование к трехмерной картинке imageShow(new_im)

Кроме того, можно воспользоваться функцией Optimal_Clusters_KMeans (которая неявно использует KMeans_rcpp), чтобы определить оптимальное количество кластеров. Доступны такие критерии: variance_explained, WCSSE (within-cluster-sum-of-squared-error - сумма-квадратов-ошибок-внутри-кластера), dissimilarity, silhouette, distortion_fK, AIC, BIC и Adjusted_Rsquared. В документации по пакету есть больше информации по каждому критерию.

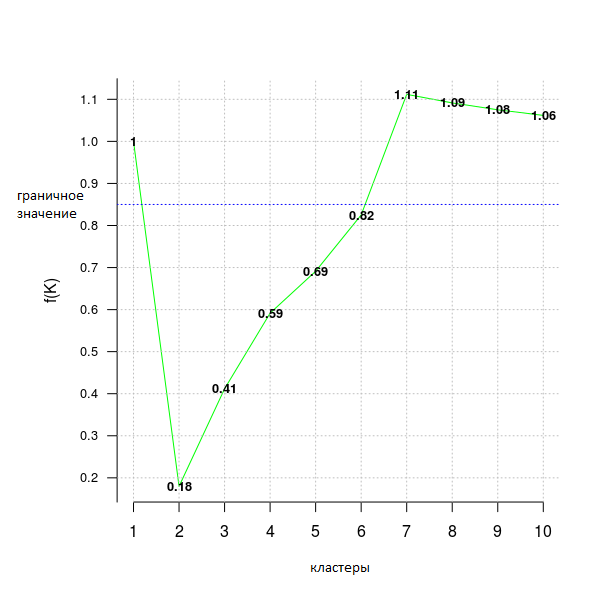
В следующем примере кода используется критерий distortion_fK, который полностью описан в статье -Selection of K in K-means clustering, Pham., Dimov., Nguyen., (2004)- («Выбор К в кластеризации методом К-средних»).

opt = Optimal_Clusters_KMeans(im2, max_clusters = 10, plot_clusters = T,                                verbose = F, criterion = 'distortion_fK', fK_threshold = 0.85)

Значения меньше фиксированной границы (здесь fK_threshold = 0.85) можно рекомендовать для кластеризации. Однако, существует более одного оптимального разбиения на кластеры, поэтому f(K) следует использовать только для предположения об их количестве, но окончательное решение, принимать это значение или нет - за пользователем.

Метод k-средних в мини-группах

Метод k-средних в мини-группах - вариация классического алгоритма k-средних. Он особенно полезен для больших наборов данных, поскольку вместо использования всего набора (как в k-средних) берутся мини-группы из случайных значений данных, чтобы оптимизировать целевую функцию.

Параметры алгоритма MiniBatchKmeans почти такие же, как и функции KMeans_rcpp из пакета ClusterR. Наиболее важная разница - параметр batch_size (размер мини-групп) и init_fraction (процент данных для определения исходных центроидов, который применяется, если initializer равен -kmeans++- или -quantile_init-).

Воспользуюсь примером векторного квантования, чтобы показать разницу во времени вычисления и качестве вывода функций KMeans_rcpp и MiniBatchKmeans.

path_d = 'dog.jpg' im_d = readImage(path_d)  # сначала изменим размер картинки, чтобы уменьшить количество измерений im_d = resizeImage(im_d, 350, 350, method = 'bilinear')             imageShow(im_d)                                                # вывод исходного изображения

im3 = apply(im_d, 3, as.vector)                                # векторизированный RGB dim(im3)                                              # исходные измерения данных

# 122500      3

Сначала выполним кластеризацию k-средних.

start = Sys.time() km_init = KMeans_rcpp(im3, clusters = 5, num_init = 5, max_iters = 100,                      initializer = 'kmeans++', threads = 1, verbose = F) end = Sys.time() t = end - start cat('time to complete :', t, attributes(t)$units, '
')  # время выполнения : 2.44029 secs  getcent_init = km_init$centroids getclust_init = km_init$clusters new_im_init = getcent_init[getclust_init, ]  # каждое значение ассоциируется с ближайшим центроидом dim(new_im_init) = c(nrow(im_d), ncol(im_d), 3)     # обратное преобразование к трехмерной картинке imageShow(new_im_init)

Теперь кластеризацию k-средних в мини-группах.

start = Sys.time() km_mb = MiniBatchKmeans(im3, clusters = 5, batch_size = 20, num_init = 5, max_iters = 100,                          init_fraction = 0.2, initializer = 'kmeans++', early_stop_iter = 10,                         verbose = F) pr_mb = predict_MBatchKMeans(im3, km_mb$centroids) end = Sys.time() t = end - start cat('time to complete :', t, attributes(t)$units, '
')  # время выполнения : 0.8346727 secs   getcent_mb = km_mb$centroids new_im_mb = getcent_mb[pr_mb, ]   # каждое значение ассоциируется с ближайшим центроидом dim(new_im_mb) = c(nrow(im_d), ncol(im_d), 3)     # обратное преобразование к трехмерной картинке imageShow(new_im_mb)

Несмотря на небольшую разницу в качестве вывода, k-средних в мини-группах возвращает результат в среднем в два раза быстрее, чем классический метод k-средних для этого набора данных.

Чтобы реализовать метод k-средних в мини-группах, я использовал следующие ресурсы:

Источник: habrahabr.ru

Кластеризация с пакетом ClusterR, часть 1

Комментарии: