Стилизация изображений с помощью нейронных сетей: никакой мистики, просто матан

Приветствую тебя, Хабр! Наверняка вы заметили, что тема стилизации фотографий под различные художественные стили активно обсуждается в этих ваших интернетах. Читая все эти популярные статьи, вы можете подумать, что под капотом этих приложений творится магия, и нейронная сеть действительно фантазирует и перерисовывает изображение с нуля. Так уж получилось, что наша команда столкнулась с подобной задачей: в рамках внутрикорпоративного хакатона мы сделали стилизацию видео, т.к. приложение для фоточек уже было. В этом посте мы с вами разберемся, как это сеть "перерисовывает" изображения, и разберем статьи, благодаря которым это стало возможно. Рекомендую ознакомиться с прошлым постом перед прочтением этого материала и вообще с основами сверточных нейронных сетей. Вас ждет немного формул, немного кода (примеры я буду приводить на Theano и Lasagne), а также много картинок. Этот пост построен в хронологическом порядке появления статей и, соответственно, самих идей. Иногда я буду его разбавлять нашим недавним опытом. Вот вам мальчик из ада для привлечения внимания.

Visualizing and Understanding Convolutional Networks (28 Nov 2013)

Первым делом стоит упомянуть статью, в которой авторы смогли показать, что нейронная сеть - это не черный ящик, а вполне даже интерпретируемая вещь (кстати, сегодня это можно сказать не только о сверточных сетях для компьютерного зрения). Авторы решили научиться интерпретировать активации нейронов скрытых слоев, для этого они использовали деконволюционную нейронную сеть (deconvnet), предложенную несколькими годами ранее (кстати, теми же Зейлером и Фергусом, которые являются авторами и этой публикации). Деконволюционная сеть - это на самом деле такая же сеть со свертками и пулингами, но примененными в обратном порядке. В оригинальной работе по deconvnet сеть использовалась в режиме обучения без учителя для генерации изображений. В этот раз авторы применили ее просто для обратного прохода от признаков, полученных после прямого прохода по сети, до исходного изображения. В итоге получается изображение, которое можно интерпретировать как сигнал, вызвавший данную активацию на нейронах. Естественно, возникает вопрос: а как сделать обратный проход через свертку и нелинейность? А тем более через max-пулинг, это уж точно не инвертируемая операция. Рассмотрим все три компонента.

Обратный ReLu

В сверточных сетях в качестве функции активации часто используется ReLu(x) = max(0, x), который делает все активации на слое не отрицательными. Соответственно, при обратном проходе через нелинейность необходимо получить также не отрицательные результаты. Для этого авторы предлагают использовать этот же ReLu. С точки зрения архитектуры Theano необходимо переопределить функцию градиента операции (бесконечно ценный ноутбук находится в рецептах лазаньи, оттуда вы почерпнете детали того, что за класс ModifiedBackprop).

class ZeilerBackprop(ModifiedBackprop):     def grad(self, inputs, out_grads):         (inp,) = inputs         (grd,) = out_grads         #return (grd * (grd > 0).astype(inp.dtype),)  # explicitly rectify         return (self.nonlinearity(grd),)  # use the given nonlinearity

Обратная свертка

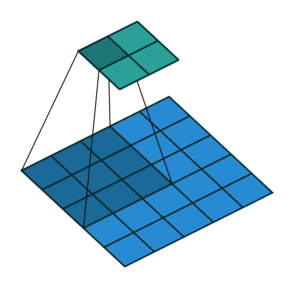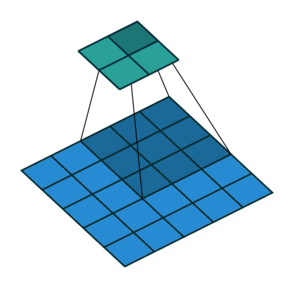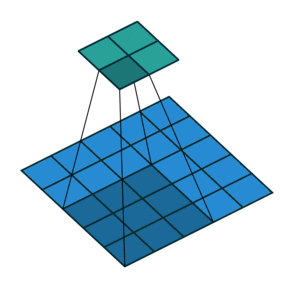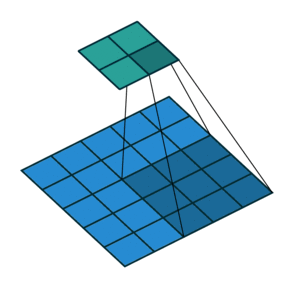
Тут немного сложнее, но все логично: достаточно применить транспонированную версию того же ядра свертки, но к выходам из обратного ReLu вместо предыдущего слоя, используемого при прямом проходе. Но боюсь, что на словах это не так очевидно, посмотрим на визуализацию этой процедуры (тут вы найдете еще больше визуализаций сверток).

Свертка при stride=1

Свертка при stride=1	Обратная версия

Свертка при stride=2

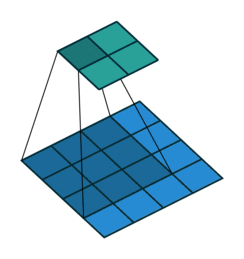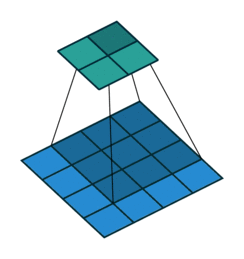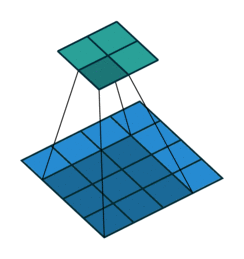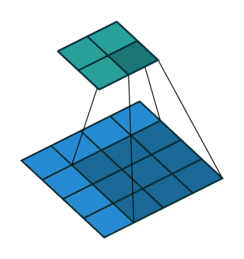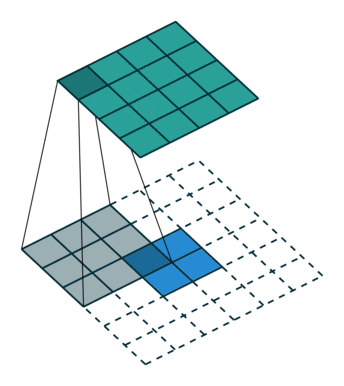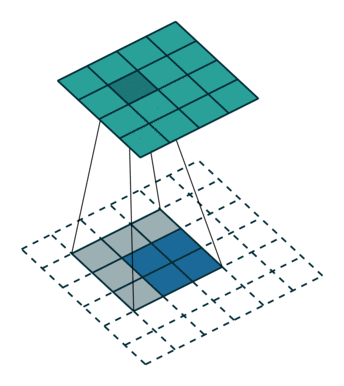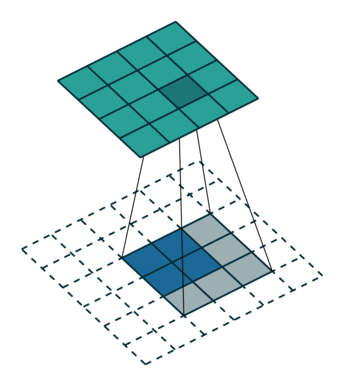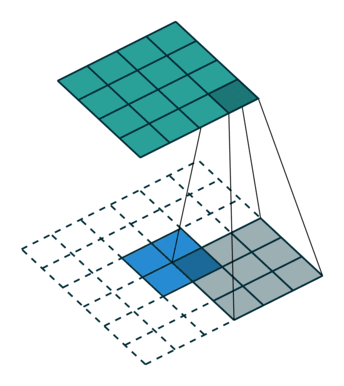Свертка при stride=2	Обратная версия

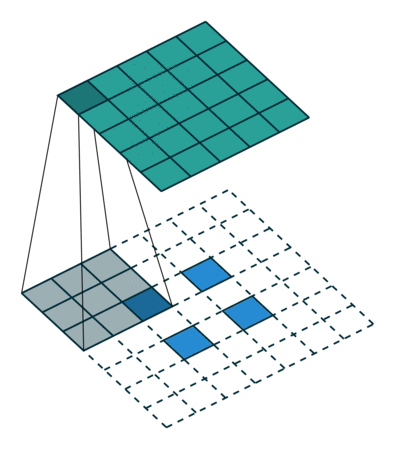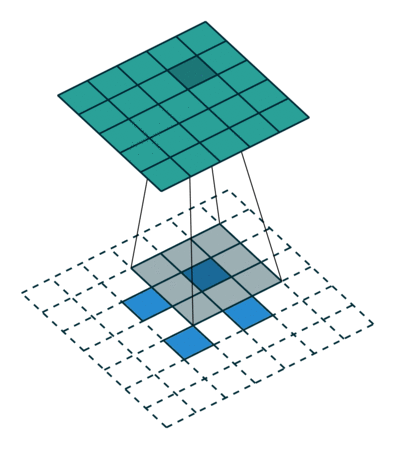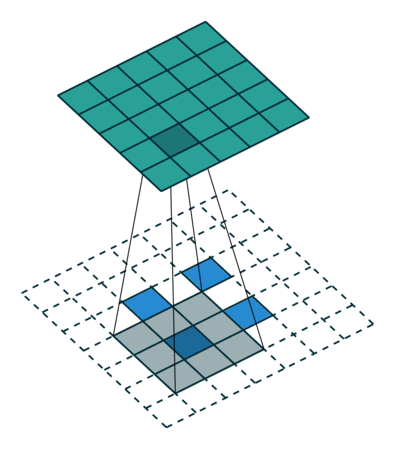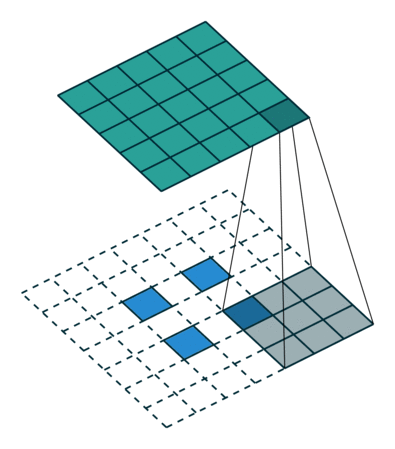Обратный пулинг

Вот эта операция (в отличие от предыдущих) вообще говоря не инвертируема. Но нам все же хотелось бы при обратном проходе каким-то способом пройти через максимум. Для этого авторы предлагают использовать карту того, где был максимум при прямом проходе (max location switches). При обратном проходе входной сигнал в анпулинг преобразуется так, чтобы приближенно сохранить структуру исходного сигнала, тут действительно проще увидеть, чем описать.

Результат

Алгоритм визуализации крайне прост:

1. Сделать прямой проход.
2. Выбрать интересующий нас слой.
3. Зафиксировать активации одного или нескольких нейронов и обнулить остальные.
4. Сделать обратный вывод.

Каждый серый квадрат на изображении ниже соответствует визуализации фильтра (который применяется для свертки) или весов одного нейрона, а каждая цветная картинка - это та часть оригинального изображения, которая активирует соответствующий нейрон. Для наглядности нейроны внутри одного слоя сгруппированы в тематические группы. В общем внезапно оказалось, что нейронная сеть выучивает ровно то, о чем писали Хьюбел и Вейзел в работе про структуру зрительной системы, за что и были удостоены Нобелевской премии в 1981 году. Благодаря этой статье мы получили наглядное представление того, что выучивает сверточная нейронная сеть на каждом слое. Именно эти знания позволят позже манипулировать содержимым генерируемого изображения, но до этого еще далеко, следующие несколько лет ушли на совершенствование способов "трепанации" нейронных сетей. Помимо этого, авторы статьи предложили способ анализа, как лучше выстраивать архитектуру сверточной нейронной сети для достижения лучших результатов (правда, ImageNet 2013 они так и не выиграли, но попали в топ; UPD: таки оказывается выиграли, Clarifai это они и есть).

Визуализация фич

Вот пример визуализации активаций, используя deconvnet, сегодня этот результат смотрится уже так себе, но тогда это был прорыв.

Saliency Maps, используя deconvnet

Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps (19 Apr 2014)

Данная статья посвящена исследованию методов визуализации знаний, заключенных в сверточной нейронной сети. Авторы предлагают два способа визуализации, основанных на градиентном спуске.

Class Model Visualisation

Итак, представьте, что у нас есть обученная нейронная сеть для решения задачи классификации на какое-то количество классов. Обозначим за значение активации выходного нейрона, который соответствует классу c. Тогда следующая задача оптимизации дает нам ровно то изображение, которое максимизирует выбранный класс:

Такую задачу легко решить, используя Theano. Обычно мы просим фреймворк взять производную по параметрам модели, но в этот раз мы считаем, что параметры фиксированы, а производная берется по входному изображению. Следующая функция выбирает максимальное значение выходного слоя и возвращает функцию, которая вычисляет производную по входному изображению.

def compile_saliency_function(net):     """     Compiles a function to compute the saliency maps and predicted classes     for a given minibatch of input images.     """     inp = net['input'].input_var     outp = lasagne.layers.get_output(net['fc8'], deterministic=True)     max_outp = T.max(outp, axis=1)     saliency = theano.grad(max_outp.sum(), wrt=inp)     max_class = T.argmax(outp, axis=1)     return theano.function([inp], [saliency, max_class])

Вы наверняка видели в интернетах странные изображения с мордами собак - DeepDream. В оригинальной статье авторы используют следующий процесс для генерации изображений, которые максимизируют выбранный класс:

1. Инициализировать начальное изображение нулями.
2. Вычислить значение производной по этому изображению.
3. Изменить изображение, прибавив к нему полученное изображение от производной.
4. Вернуться к пункту 2 или выйти из цикла.

Получаются такие вот изображения:

А если инициализировать первое изображение реальной фотографией и запустить этот же процесс? Но на каждой итерации будем выбирать случайный класс, обнулять остальные и вычислять значение производной, то получится вот такой вот deep dream.

Осторожно 60 мб

Почему же столько морд собак и глаз? Все просто: в имаджнете из 1000 классов почти 200 собак, у них есть глаза. А также много классов, где просто есть люди.

Class Saliency Extraction

Если этот процесс инициализировать реальной фотографией, остановить после первой итерации и отрисовать значение производной, то мы получим такое изображение, прибавив которое к исходному, мы увеличим значение активации выбранного класса.

Saliency Maps, используя производную

Опять результат "так себе". Важно отметить, что это новый способ визуализации активаций (ничто же не мешает нам фиксировать значения активаций не на последнем слое, а вообще на любом слое сети и брать производную по входному изображению). Следующая статья объединит оба предыдущих подхода и даст нам инструмент к тому, как настраивать трансфер стиля, который будет описан позже.

Striving for Simplicity: The All Convolutional Net (13 Apr 2015)

Данная статья вообще говоря не о визуализации, а о том, что замена пулинга сверткой с большим страйдом не приводит к потере качества. Но как побочный продукт своих изысканий авторы предложили новый способ визуализации фич, который они применили для более точного анализа того, что выучивает модель. Их идея в следующем: если мы просто берем производную, то при деконволюции обратно не проходят те фичи, которые были на входном изображении меньше нуля (применение ReLu для входного изображения). И это приводит к тому, что на пропагируемом обратно изображении появляются отрицательные значения. С другой стороны, если использовать deconvnet, то от производной ReLu берется еще один ReLu - это позволяет не пропускать обратно отрицательные значения, но как вы видели результат получается "так себе". Но что если объединить эти два метода?

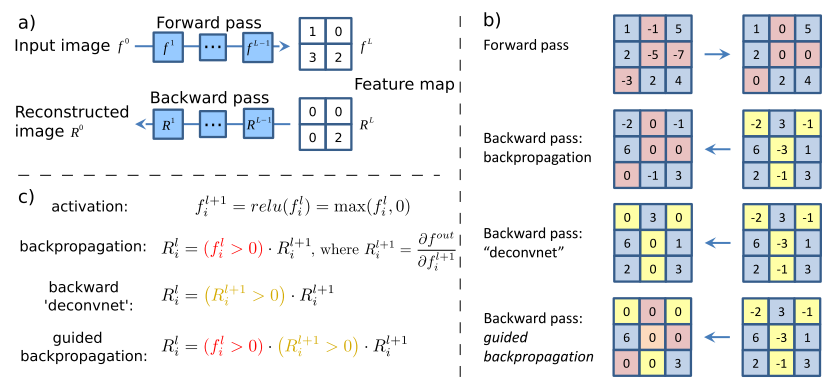
class GuidedBackprop(ModifiedBackprop):     def grad(self, inputs, out_grads):         (inp,) = inputs         (grd,) = out_grads         dtype = inp.dtype         return (grd * (inp > 0).astype(dtype) * (grd > 0).astype(dtype),)

Тогда получится вполне чистое и интерпретируемое изображение.

Saliency Maps, используя Guided Backpropagation

Go deeper

Теперь давайте задумаемся, а что нам это дает? Позволю себе напомнить, что каждый сверточный слой - это функция, которая получает на вход трехмерный тензор и на выход тоже выдает трехмерный тензор, быть может, другой размерности d x w x h; depth - это количество нейронов в слое, каждый из них генерит плашку (feature map) размером wigth x height.

Давайте попробуем провести следующий эксперимент на сети VGG-19:

• для каждого слоя нейронной сети, будем сортировать плашки по значению суммы активаций внутри плашек
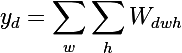
  - это даст нам наиболее выраженные признаки на изображении (в одной плашке находятся активации одной и той же фичи в разных пространственных координатах);
• затем на каждой плашке будем выбирать максимальный элемент - это даст нам позицию, где данная фича выражена наиболее четко;
• а теперь возьмем производную по входному изображению при фиксированном значении одной позиции на одной плашке и обнуленными остальными значениями в слое - это даст нам представление о фиче, а также о рецептивной области этого нейрона (того, на какую область изображения смотрит этот нейрон).

conv1_2

Да вы почти ничего не видите, т.к. рецептивная область очень маленькая, это вторая свертка 3х3, соответственно общая область 5х5. Но увеличив, мы увидим, что фича - это просто детектор градиента.

conv3_3

conv4_3

conv5_3

pool5

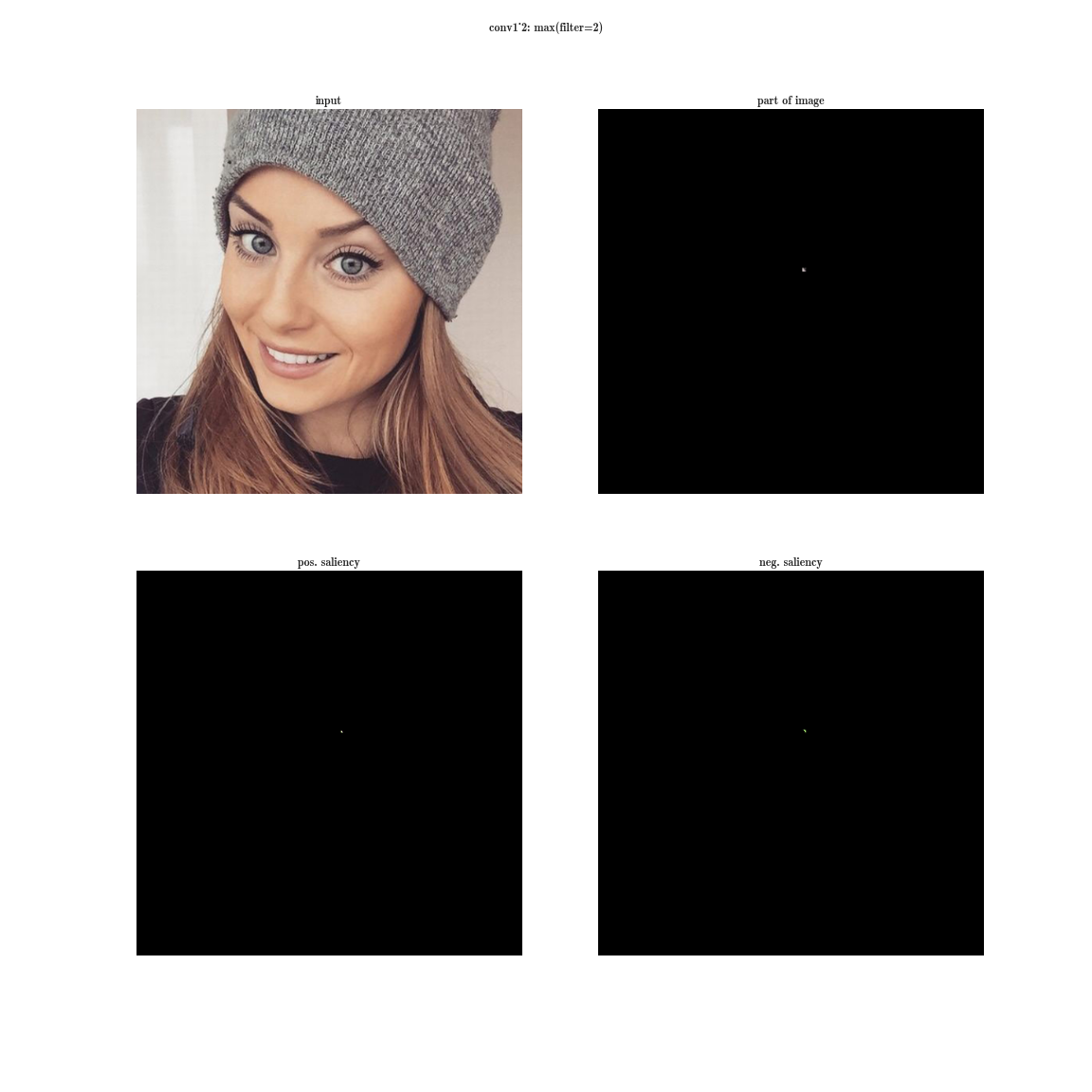
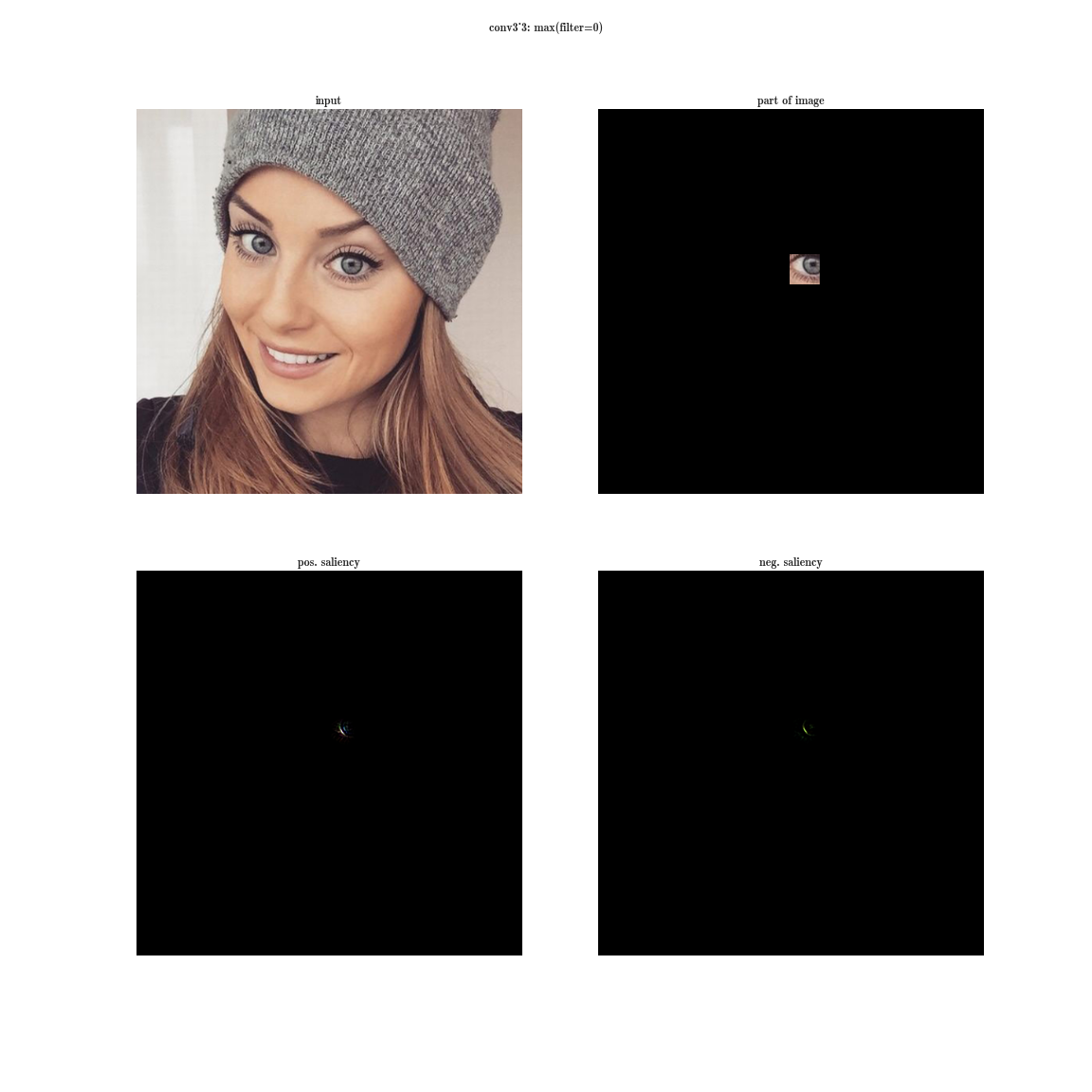
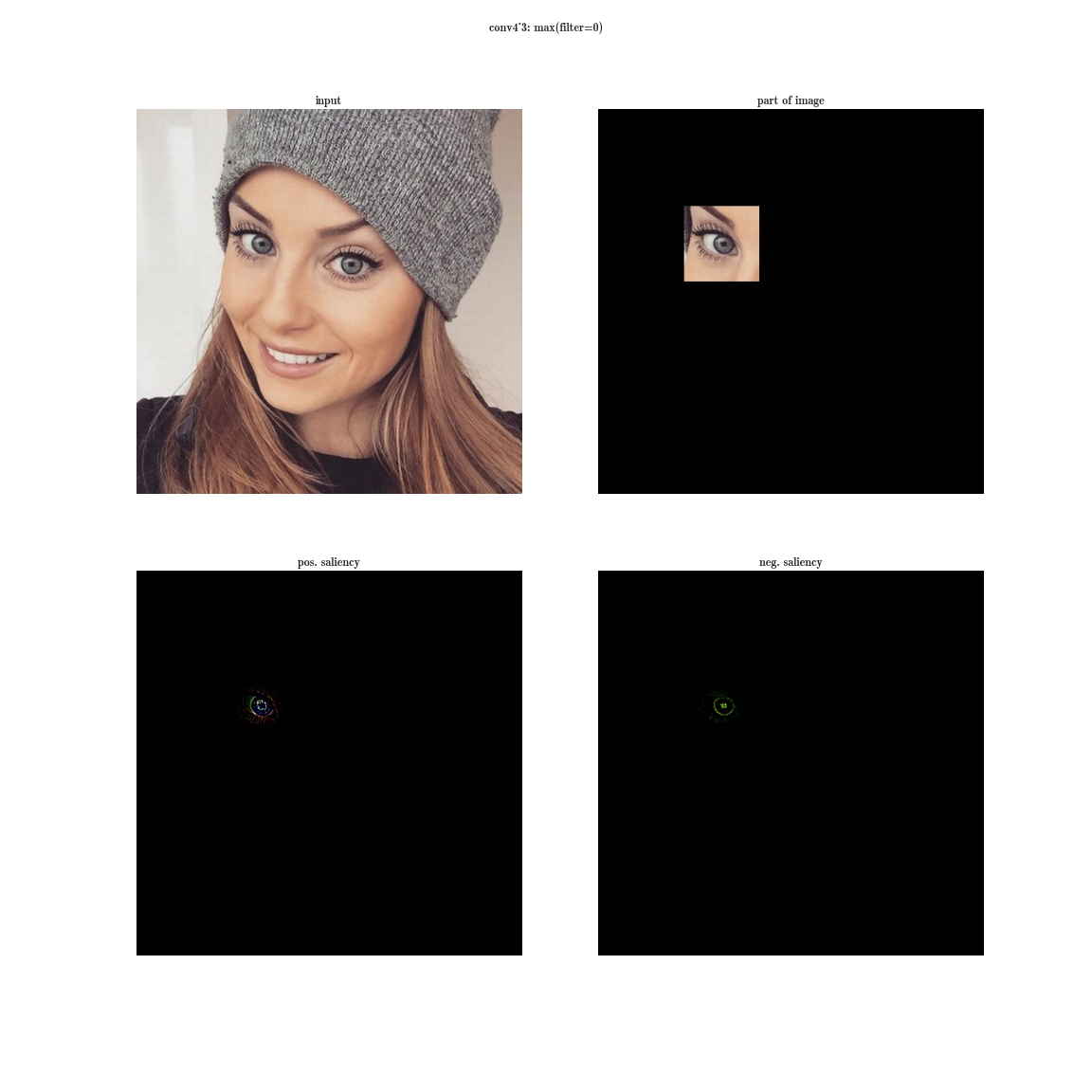
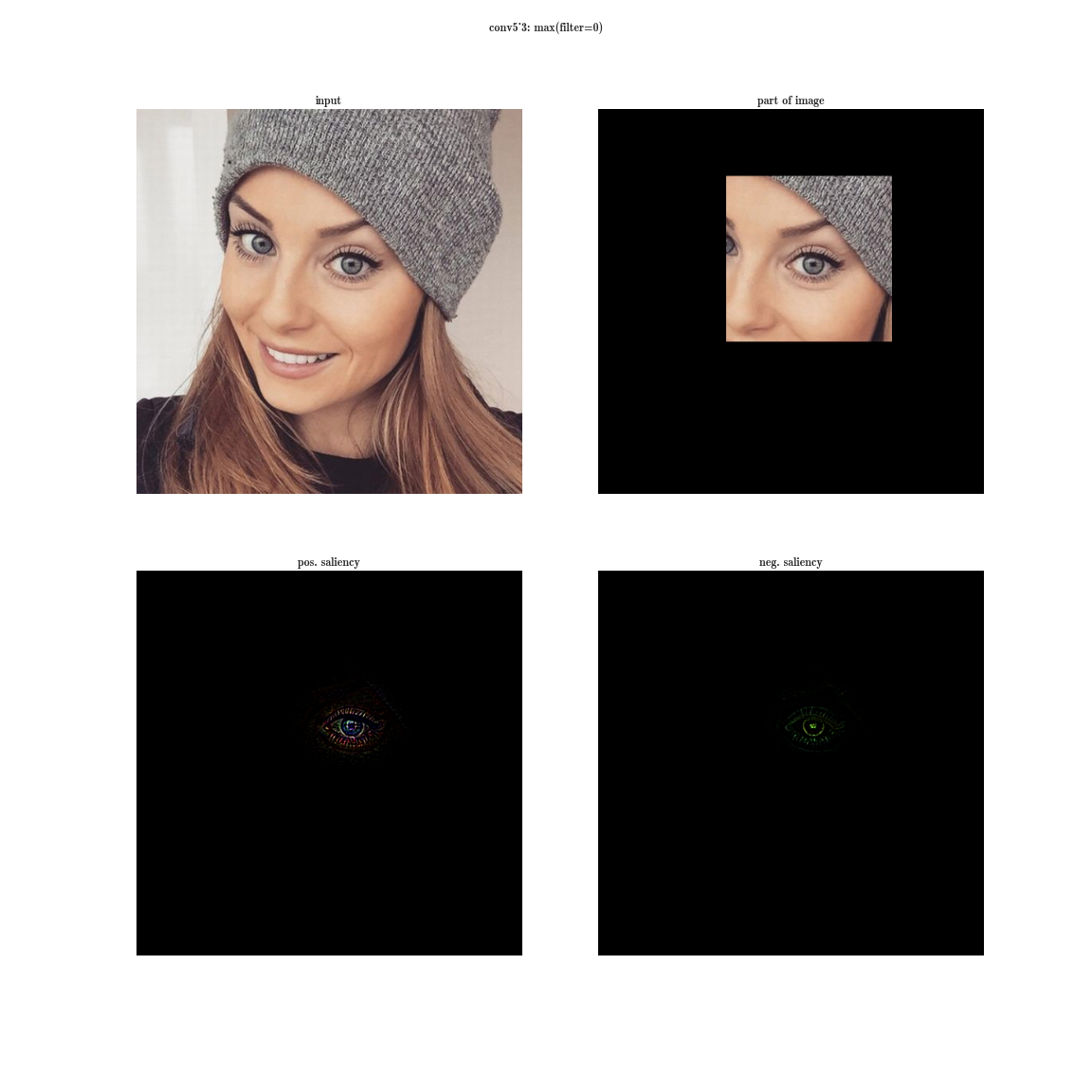
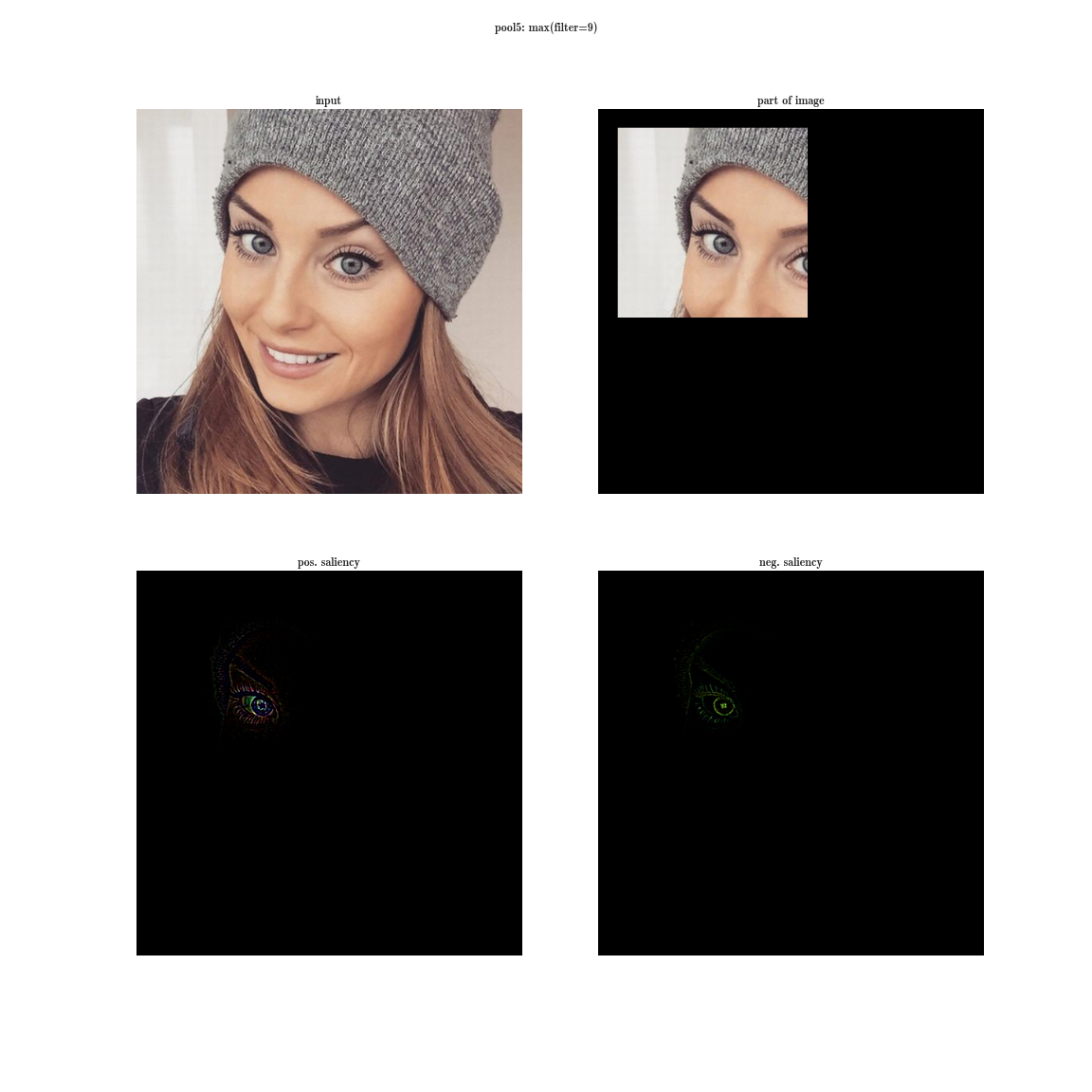
А теперь представим, что вместо максимума по плашке мы будем брать производную значения суммы всех элементов плашки по входному изображению. Тогда очевидно рецептивная область группы нейронов будет покрывать все входное изображение. Для ранних слоев мы увидим яркие карты, из которых мы делаем вывод, что это детекторы цветов, затем градиентов, затем границ и так далее в сторону усложнения паттернов. Чем глубже слой, тем более тусклое изображение получается. Это объясняется тем, что у более глубоких слоев, более сложный паттерн, который они детектируют, а сложный паттерн появляется реже, чем простой, потому и карта активаций тускнеет. Первый способ подходит для понимания слоев со сложными паттернами, а второй - как раз для простых.

conv1_1

conv2_2

conv4_3

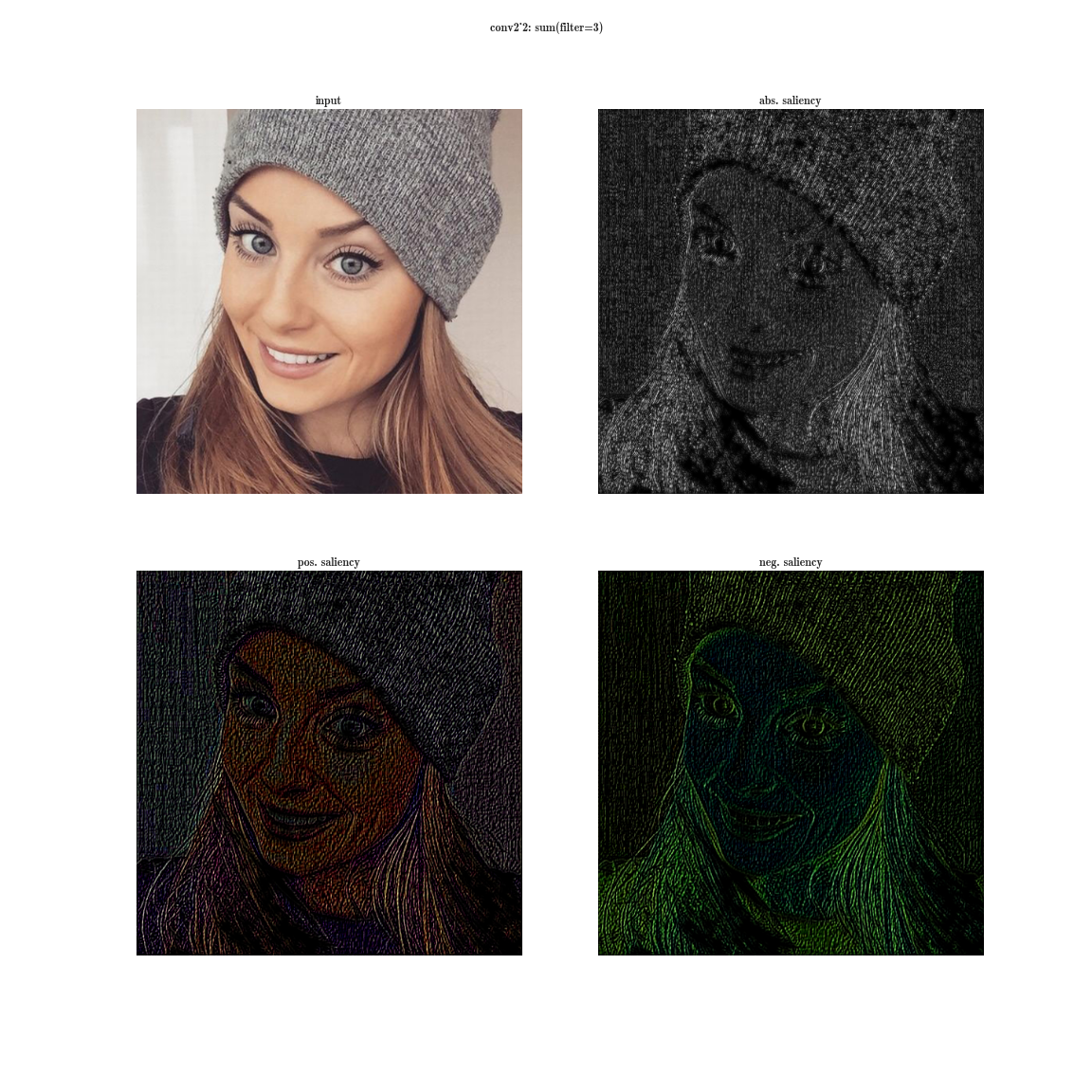
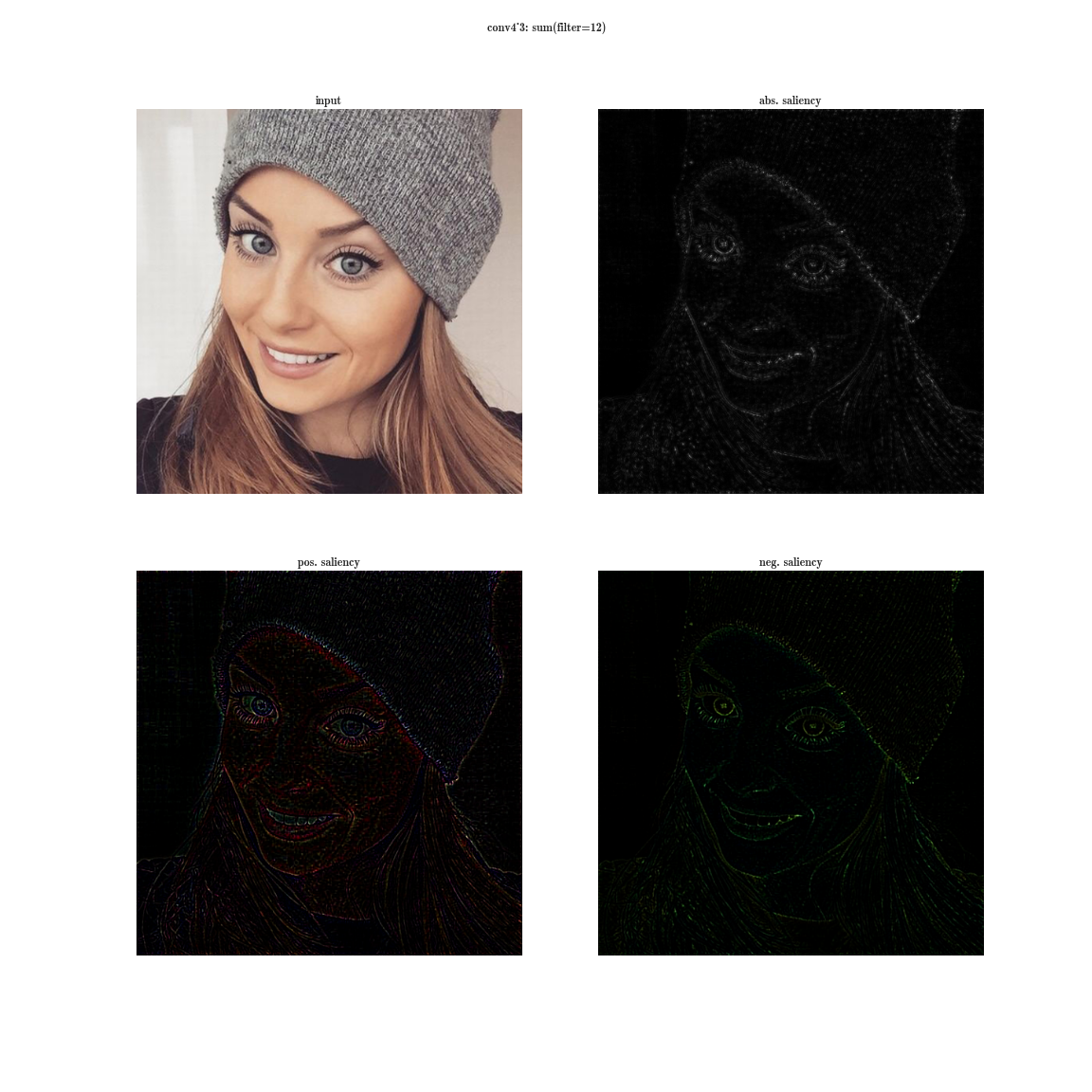
Более полную базу активаций вы можете скачать для нескольких изображений тут и тут.

A Neural Algorithm of Artistic Style (2 Sep 2015)

Итак, прошло пару лет с момента первой удачной трепанации нейронной сети. У нас (в смысле - у человечества) есть на руках мощный инструмент, который позволяет понять, что выучивает нейронная сеть, а также убрать то, что нам не очень хотелось бы что бы она выучивала. Авторы данной статьи разрабатывают метод, который позволяет сделать так, чтобы одно изображение генерировало похожую карту активаций на какое то целевое изображение, а возможно даже и не на одно - это и лежит в основе стилизации. На вход мы подаем белый шум, и похожим итеративным процессом как в deep dream мы приводим это изображение к такому, у которого карты признаков похожи на целевое изображение.

Content Loss

Как уже было упомянуто, каждый слой нейронной сети производит трехмерный тензор некоторой размерности.

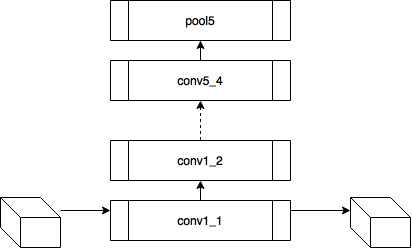
Обозначим выход i-ого слоя от входной как . Тогда если мы будем минимизировать взвешенную сумму невязок между входным изображением
и некоторым изображением, к которому мы стремимся c, то получится ровно то, что нужно. Наверное.

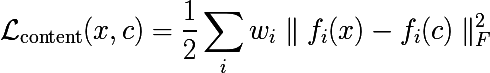
Для экспериментов с этой статьей можно использовать этот волшебный ноутбук, там происходят вычисления (как на ГПУ, так и на ЦПУ). ГПУ используется для вычисления фич нейросети и значения функции стоимости. Theano выдает функцию, которая умеет вычислять градиент целевой функции eval_grad по входному изображению x. Затем это все подается в lbfgs и запускается итеративный процесс.

# Initialize with a noise image generated_image.set_value(floatX(np.random.uniform(-128, 128, (1, 3, IMAGE_W, IMAGE_W))))  x0 = generated_image.get_value().astype('float64') xs = [] xs.append(x0)  # Optimize, saving the result periodically for i in range(8):     print(i)     scipy.optimize.fmin_l_bfgs_b(eval_loss, x0.flatten(), fprime=eval_grad, maxfun=40)     x0 = generated_image.get_value().astype('float64')     xs.append(x0)

Если же мы запустим оптимизацию такой функции, то мы быстро получим изображение, похожее на целевое. Теперь мы умеем из белого шума воссоздавать изображения, похожие на некоторое content-изображение.

Content Loss: conv4_2

Content Image

Процесс оптимизации

Легко заметить две особенности полученного изображения:

• потерялись цвета - это результат того, что в конкретном примере использовался только слой conv4_2 (или, другими словами, вес w при нем был ненулевой, а для остальных слоев нулевой); как вы помните, именно ранние слои содержат информацию о цветах и градиентных переходах, а поздние содержат информацию о более крупных деталях, что мы и наблюдаем - цвета потеряны, а контент нет;
• некоторые дома «поехали», т.е. прямые линии слегка искривились - это потому что чем более глубокий слой, тем меньше информации о пространственном положении фичи в нем содержится (результат применения сверток и пулингов).

Добавление ранних слоев сразу исправляет ситуацию с цветами.

Content Loss: conv1_1, conv2_1, conv4_2

Надеюсь, к этому моменту вы ощутили, что вы можете управлять тем, что будет перерисовано на изображение из белого шума.

Style Loss

И вот мы добрались до самого интересного: а как же нам передать стиль? Что такое стиль? Очевидно, что стиль - это не то что мы оптимизировали в Content Loss'е, ведь там содержится много информации о пространственных положениях фичей. Так что первое, что нужно сделать, - это каким-либо способом убрать эту информацию из представлений, полученных на каждом слое.

Автор предлагает следующий способ. Возьмем тензор на выходе из некоторого слоя, развернем по пространственным координатам и посчитаем матрицу ковариации между плашками. Обозначим это преобразование как G. Что мы на самом деле сделали? Можно сказать, что мы посчитали, как часто признаки внутри плашки встречаются попарно, или, другими словами, мы аппроксимировали распределение признаков в плашках многомерным нормальным распределением.

Тогда Style Loss вводится следующим образом, где s - это некоторое изображение со стилем:

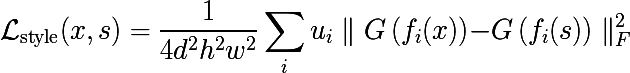
Попробуем для Винсента? Получим в принципе что-то ожидаемое - шум в стиле Ван Гога, информация о пространственном расположении фичей полностью потеряна.

Винсент

А что если вместо стилевого изображения поставить фотографию? Получится уже знакомые фичи, знакомые цвета, но пространственное положение полностью потеряно.

Фото при style loss

Наверняка вы задались вопросом о том, а почему мы вычисляем именно матрицу ковариации, а не что то другое? Ведь существует много способов того, как агрегировать признаки так, чтобы потерялись пространственные координаты. Это действительно вопрос открытый, и если взять что-то очень простое, то результат изменится не драматически. Давайте проверим это, будем вычислять не матрицу ковариации, а просто среднее значение каждой плашки.

простой style loss

Комбинированный лосс

Естественно, возникает желание смешать эти две функции стоимости. Тогда мы из белого шума будем генерировать такое изображение, что в нем будут сохранены признаки из content-изображения (у которых есть привязка к пространственным координатам), а также будут присутствовать "стилевые" признаки, не привязанные к пространственным координатам, т.е. мы будем надеяться, что детали изображения контента останутся нетронутыми со своих мест, но будут перерисованы с нужным стилем.

На самом деле присутствует еще и регуляризатор, но мы его опустим для простоты. Остается ответить на следующий вопрос: а какие слои (веса) использовать при оптимизации? И боюсь, что ответа на этот вопрос у меня нет, да и у авторов статьи тоже. У них есть предложение использовать следующие, но это совсем не значит, что другая комбинация будет работать хуже, слишком большое пространство поиска. Единственное правило, которое следует из понимания модели: нет смысла брать соседние слои, т.к. у них признаки будут отличаться друг от друга не сильно, потому в стиль добавляется по слою из каждой группы conv*_1.

# Define loss function losses = []  # content loss losses.append(0.001 * content_loss(photo_features, gen_features, 'conv4_2'))  # style loss losses.append(0.2e6 * style_loss(art_features, gen_features, 'conv1_1')) losses.append(0.2e6 * style_loss(art_features, gen_features, 'conv2_1')) losses.append(0.2e6 * style_loss(art_features, gen_features, 'conv3_1')) losses.append(0.2e6 * style_loss(art_features, gen_features, 'conv4_1')) losses.append(0.2e6 * style_loss(art_features, gen_features, 'conv5_1'))  # total variation penalty losses.append(0.1e-7 * total_variation_loss(generated_image))  total_loss = sum(losses)

Итоговую модель можно представить в следующем виде.

А вот результат домиков с Ван Гогом.

Попытка контролировать процесс

Давайте вспомним предыдущие части, уже как два года до текущей статьи, другие ученые исследовали, что же действительно выучивает нейронная сеть. Вооружившись всеми этими статьями, можно нагенерить визуализации фич различных стилей, различных изображений, различных разрешений и размеров, и попытаться понять, какие слои с каким весом брать. Но даже перевзвешивание слоев не дает полного контроля над происходящим. Проблема здесь более концептуальная: мы ведь оптимизируем не ту функцию! Как так, спросите вы? Ответ простой: эта функция минимизирует невязку- ну вы поняли. Но что мы действительно хотим - это то, чтобы изображение нам понравилось. Выпуклая комбинация content и style loss функций не является мерилом того, что наш разум считает красивым. Было замечено, что если продолжать стилизацию слишком долго, то функция стоимости естественно падает ниже и ниже, а вот эстетическая красота результата резко падает.

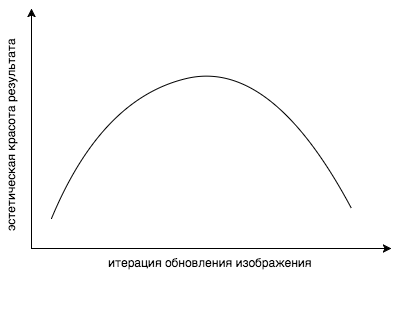
Ну да ладно, есть еще одна проблема. Допустим, мы нашли слой, который извлекает нужные нам признаки. Допустим, какие-то текстурки треугольные. Но этот слой еще содержит множество других признаков, например кружочков, которые мы очень не хотим видеть на результирующем изображении. Вообще говоря, если бы можно было нанять миллион китайцев, то можно было бы визуализировать все фичи стилевого изображения, и полным перебором просто отметить те, которые нам нужны, и только их включить в функцию стоимости. Но по понятным причинам это не так просто. Но что если мы просто удалим все кружочки, которые мы не хотим видеть на результате, из стилевого изображения? Тогда просто не сработают активации соответствующих нейронов, которые реагируют на кружочки. И, естественно, тогда в результирующей картинке этого не появится. То же самое и с цветами. Представьте яркое изображение с большим количеством цветов. Распределение цветов будет очень размазанным по всему пространству, таким же будет и распределение у результирующего изображения, но вот в процессе оптимизации наверняка потеряются те пики, которые были на оригинале. Оказалось, что простое уменьшение разрядности цветовой палитры решает эту проблему. Плотность распределения большинства цветов будет около нуля, и будут большие пики на нескольких участках. Таким образом, манипулируя оригиналом в фотошопе, мы манипулируем признаками, которые извлекаются из изображения. Человеку проще выразить свои желания визуально, нежели пытаться сформулировать их на языке математики. Пока. В итоге, дизайнеры и менеджеры, вооружившись фотошопом и скриптами для визуализации признаков, добились раза в три быстрее результата лучше, чем тот, что сделали математики с программистами.

Пример манипуляции цветом и размером фичей

Оригинал	Деградированная версия

А можно в качестве стиля взять сразу простое изображение

Стиль

Результаты

Texture Networks: Feed-forward Synthesis of Textures and Stylized Images (10 Mar 2016)

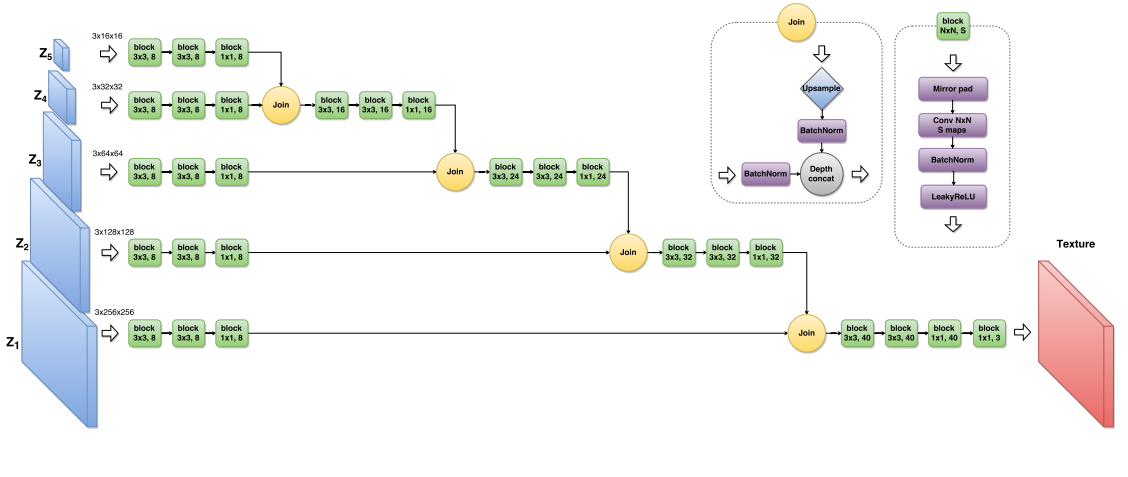
Вроде бы на этом можно было остановиться, если не один нюанс. Вышеописанный алгоритм стилизации работает очень долго. Если взять реализацию, где lbfgs запускается на ЦПУ, то процесс занимает минут пять. Если переписать так, чтобы и оптимизация шла в ГПУ, то процесс будет занимать 10-15 секунд. Это никуда не годится. Возможно авторы этой и следующей статьи думали примерно так же. Обе публикации вышли независимо с разницей в 17 дней, спустя почти год после предыдущей статьи. Авторы текущей статьи, как и авторы предыдущей, занимались генерацией текстур (если вы просто обнулите Style Loss примерно это и получится). Они предложили оптимизировать не изображение, полученное из белого шума, а некоторую нейронную сеть, которая генерирует стилизованное изображение.

Теперь если процесс стилизации не включает в себя никакой оптимизации, требуется сделать только прямой проход. А оптимизация требуется только один раз для тренировки сети-генератора. В этой статье используется иерархический генератор, где каждый следующий z размером больше предыдущего и семплируется из шума в случае генерации текстуры, и из некоторой базы изображений для тренировки стилизатора. Критично использовать что-то отличное от тренировочной части имаджнета, т.к. фичи внутри Loss-сети вычисляются сетью, обученной как раз на тренировочной части.

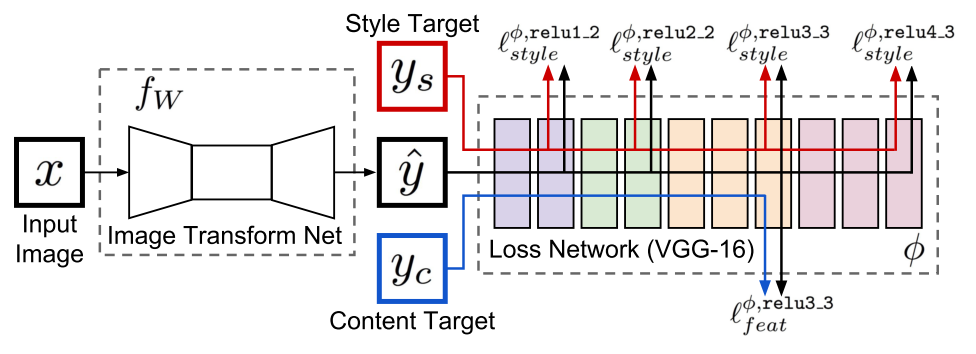
Perceptual Losses for Real-Time Style Transfer and Super-Resolution (27 Mar 2016)

Как видно из названия, авторы, которые опоздали всего на 17 дней с идеей генерирующей сети, занимались увеличением разрешения изображений. Они судя по всему были вдохновлены успехами residual learning на последнем имаджнете.

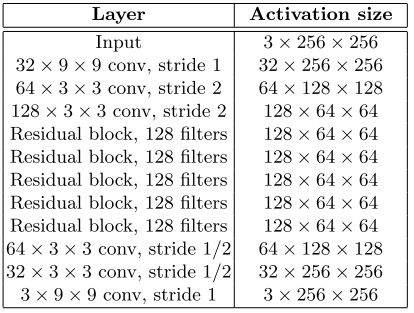
Соответственно residual block и conv block.

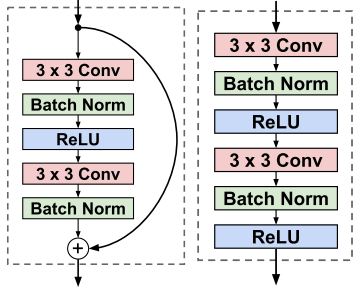
Таким образом, теперь у нас на руках помимо контроля над стилизацией есть еще и быстрый генератор (благодаря этим двум статьям время генерации одного изображения измеряется десятками мс).

Окончание

Информацию из рассмотренных статей и код авторов мы использовали как начальную точку для создания еще одного приложения для стилизации первого приложения для стилизации видео:

• Artisto на Android
• Artisto на iOS

Генерит что-то такое:

Ну и остальные полезные ссылки:

• Theano
• Lasagne
• Lasagne/Recipes, да теано+лазанья - это круто; кстати, на текущей версии TF, реализация лосс-функции занимает в ГПУ примерно 8 Гб, в то время как на Теане 700 Мб
• Lasagne/Recipes/examples/Saliency Maps and Guided Backpropagation
• Lasagne/Recipes/examples/styletransfer/Art Style Transfer
• Реализация иерархического генератора и других плюшек одним из авторов соответствующей статьи на Torch
• Реализация resnet-like генератора на неком Chainer
• Реализация модели Gatys'а на Torch, автором статьи с resnet-like генератором; данная реализация поддерживает оптимизацию в ГПУ вместо lbfgs на ЦПУ

Источник: habrahabr.ru

Комментарии: