Математика для искусственных нейронных сетей для новичков, часть 1

2016-08-26 18:44

свёрточные нейронные сети, новости нейронных сетей

Оглавление

Часть 1 - линейная регрессия
Часть 2 - градиентный спуск
Часть 3 - градиентный спуск продолжение

Введение

Этим постом я начну цикл «Нейронные сети для новичков». Он посвящен искусственным нейронным сетям (внезапно). Целью цикла является объяснение данной математической модели. Часто после прочтения подобных статей у меня оставалось чувство недосказанности, недопонимания - НС по-прежнему оставались «черным ящиком» - в общих чертах известно, как они устроены, известно, что делают, известны входные и выходные данные. Но тем не менее полное, всестороннее понимание отсутствует. А современные библиотеки с очень приятными и удобными абстракциями только усиливают ощущение «черного ящика». Не могу сказать, что это однозначно плохо, но и разобраться в используемых инструментах тоже никогда не поздно. Поэтому моей первичной целью является подробное объяснение устройства нейронных сетей так, чтобы абсолютно ни у кого не осталось вопросов об их устройстве; так, чтобы НС не казались волшебством. Так как это не математический трактат, я ограничусь описанием нескольких методов простым языком (но не исключая формул, конечно же), предоставляя поясняющие иллюстрации и примеры.

Цикл рассчитан на базовый ВУЗовский математический уровень читающего. Код будет написан на Python3.5 с numpy 1.11. Список остальных вспомогательных библиотек будет в конце каждого поста. Абсолютно все будет написано с нуля. В качестве подопытного выбрана база MNIST - это черно-белые, центрированные изображения рукописных цифр размером 28*28 пикселей. По-умолчанию, 60000 изображений отмечены для обучения, а 10000 для тестирования. В примерах я не буду изменять распределения по-умолчанию.

Пример изображений из MNIST:

Я не буду заострять внимание на структуре MNIST и просто выложу код, который загрузит базу и сохранит в нужном формате. Этот формат в дальнейшем будет использован в примерах:

loader.py

import struct import numpy as np import requests import gzip import pickle  TRAIN_IMAGES_URL = "http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz" TRAIN_LABELS_URL = "http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz"  TEST_IMAGES_URL = "http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz" TEST_LABELS_URL = "http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz"   def downloader(url: str):     response = requests.get(url, stream=True)     if response.status_code != 200:         print("Response for", url, "is", response.status_code)         exit(1)     print("Downloaded", int(response.headers.get('content-length', 0)), "bytes")     decompressed = gzip.decompress(response.raw.read())     return decompressed   def load_data(images_url: str, labels_url: str) -> (np.array, np.array):     images_decompressed = downloader(images_url)      # Big endian 4 числа типа unsigned int, каждый по 4 байта     magic, size, rows, cols = struct.unpack(">IIII", images_decompressed[:16])     if magic != 2051:         print("Wrong magic for", images_url, "Probably file corrupted")         exit(2)      image_data = np.array(np.frombuffer(images_decompressed[16:], dtype=np.dtype((np.ubyte, (rows * cols,)))) / 255,                           dtype=np.float32)      labels_decompressed = downloader(labels_url)     # Big endian 2 числа типа unsigned int, каждый по 4 байта     magic, size = struct.unpack(">II", labels_decompressed[:8])     if magic != 2049:         print("Wrong magic for", labels_url, "Probably file corrupted")         exit(2)      labels = np.frombuffer(labels_decompressed[8:], dtype=np.ubyte)      return image_data, labels   with open("test_images.pkl", "w+b") as output:     pickle.dump(load_data(TEST_IMAGES_URL, TEST_LABELS_URL), output)  with open("train_images.pkl", "w+b") as output:     pickle.dump(load_data(TRAIN_IMAGES_URL, TRAIN_LABELS_URL), output)

Линейная регрессия

Линейная регрессия - метод восстановления зависимости между двумя переменными. Линейная означает, что мы предполагаем, что переменные выражаются через уравнение вида:

Эпсилон здесь - это ошибка модели. Также для наглядности и простоты будем иметь дело с одномерной моделью - многомерность не прибавляет сложности, но иллюстрации сделать не выйдет. На секунду забудем про MNIST и сгенерируем немного данных, вытянутых в линию. Также перепишем модель (гипотезу) регрессии следующим образом:

. y с шапкой - это предсказанное моделью значение.

1 и 2 - неизвестные параметры - основная задача эти параметры отыскать, а x - свободная переменная, ее значения нам известны. Сформулируем задачу еще раз и немного другим языком - у нас есть набор экспериментальных данных в виде пар значений

и нужно найти прямую линию, на которой эти значения располагаются, найти линию, которая бы наилучшим образом обобщала экспериментальные данные. Немного кода для генерации данных:

generate_linear.py

import numpy as np import matplotlib.pyplot as plt  TOTAL = 200 STEP = 0.25   def func(x):     return 0.2 * x + 3   def generate_sample(total=TOTAL):     x = 0     while x < total * STEP:         yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8)         x += STEP   X = np.arange(0, TOTAL * STEP, STEP) Y = np.array([y for y in generate_sample(TOTAL)]) Y_real = np.array([func(x) for x in X])  plt.plot(X, Y, 'bo') plt.plot(X, Y_real, 'g', linewidth=2.0) plt.show()

В результате должно получиться что-то вроде этого - достаточно случайно для неподготовленного человеческого глаза:

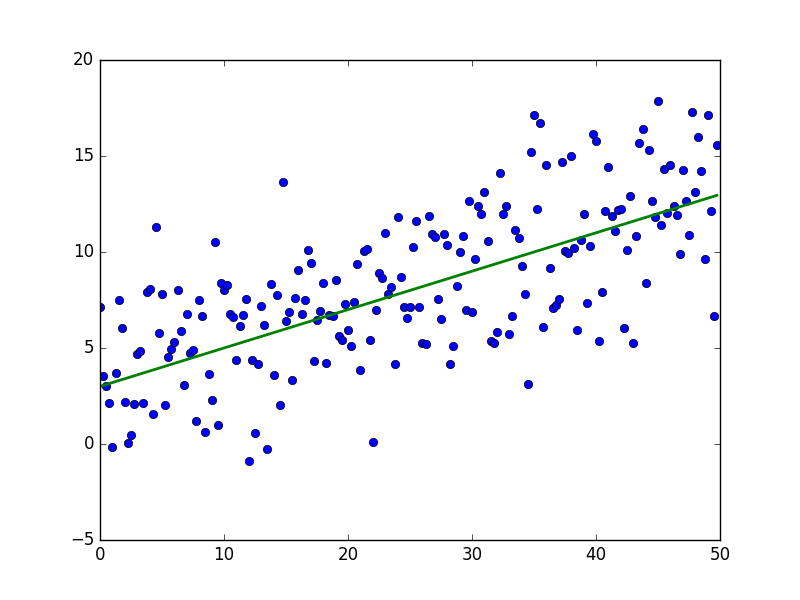
Зеленая линия - это «база» - сверху и снизу от этой линии случайным образом распределены данные, распределение равномерное. Уравнение для зеленой линии:

Метод наименьших квадратов

Суть МНК заключается в том, чтобы отыскать такие параметры

, чтобы предсказанное значение было наиболее близким к реальному. Графически это выражается как-то так:

Код

import matplotlib.pyplot as plt  plt.plot([1, 2, 3, 4, 5], [4, 2, 9, 9, 5], 'bo') plt.plot([1, 2, 3, 4, 5], [3, 5, 7, 9, 11], '-ro') plt.show()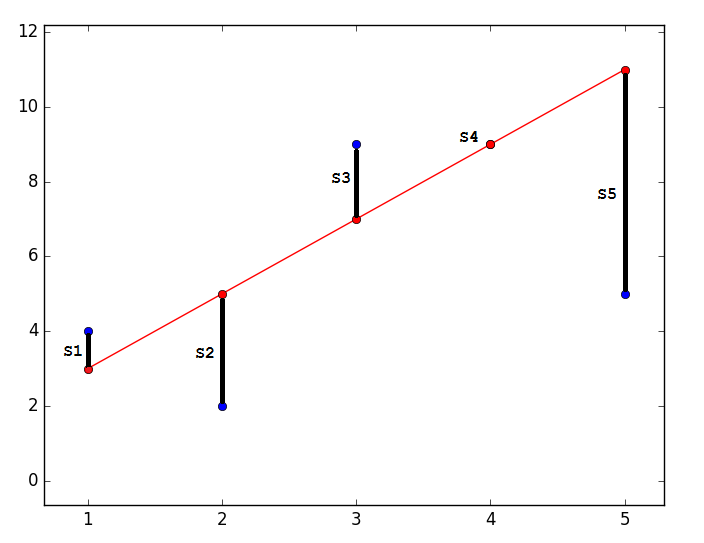

Наиболее близким - значит, что вектор

должен иметь наименьшую возможную длину. Так как вектор не единственный, то постулируется, что сумма квадратов длин всех векторов должна стремится к минимуму, учитывая вектор параметров

. На мой взгляд, довольно логичный метод, умозрительный. Тем не менее, существует математическое доказательство корректности этого метода Ремарка: под длиной будем понимать Евклидову метрику, хотя это необязательно. Ремарка 2: обратите внимание, что сумма квадратов. Опять-таки, никто не запретит попробовать минимизировать просто сумму длин. На этой картинке красные точки - предсказанное значение (

), синие - полученные в результате эксперимента(y без шапки).

- это как раз различие между ними, длина вектора.
Математически это выглядит так:

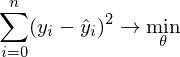
- требуется найти такой вектор

, при котором выражение

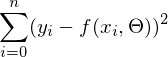достигает минимума. Функция f в этом выражении - это:

или

Я долго думал, стоит ли сразу переходить к векторизации кода и в итоге без нее статья слишком удлиняется. Поэтому введем новые обозначения:

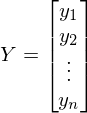
- вектор, состоящий из значений зависимой переменной y -

- вектор параметров -

A - матрица из значений свободной переменной x. В данном случае первый столбец равен 1 (отсутствует x_0) -

. В одномерном случае в матрице A только два столбца -

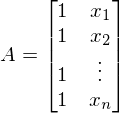
После новых обозначений уравнение линии переходит в матричное уравнение следующего вида:

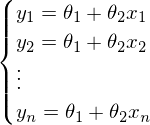
. В этом уравнении 2 неизвестных - предсказанные значения и параметры. Мы можем попробовать узнать параметры из такого же уравнения, но с известными значениями:

Иначе можно представить как систему уравнений:

Казалось бы, что все известно - и вектор Y, и вектор X - остается только решить уравнение. Большая проблема заключается в том, что система может не иметь решений - иначе, у матрицы A может не существовать обратной матрицы. Простой пример системы без решения - любые тричетыре точки не на одной прямойплоскостигиперплоскости - это приводит к тому, что матрица А становится неквадратной, а значит по определению нет обратной матрицы

.

Наглядный пример невозможности решения «простым способ» (каким-нибудь методом Гаусса решить систему):

Система выглядит так:

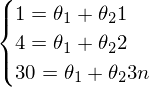- вряд ли выйдет отыскать решения для такой системы.
Как итог невозможно построить линию через эти три точки - можно лишь построить примерно верное решение.

Такое отступление - это объяснение того, зачем вообще понадобился МНК и его братья. Минимизации функции стоимости (функции потерь) и невозможность (ненужность, вредность) найти абсолютно точное решение - одни из самых базовых идей, что лежат в основе нейронных сетей. Но до них еще далеко, а пока вернемся к методу наименьших квадратов.

МНК говорит нам, что необходимо найти минимум суммы квадратов векторов вида:

Сумму квадратов с учетом того, что все преобразовано в вектораматрицы можно записать следующим образом:

.
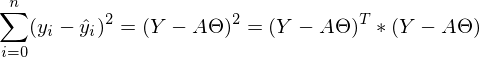У меня не повернется язык назвать это тривиальным преобразованием, новичкам бывает довольно сложно уйти от простых переменных к векторам поэтому я распишу все это выражение полностью в «раскрытых» векторах. Опять-таки, чтобы ни одна строка не была непонятым «волшебством».
Для начала просто «раскроем» вектора в соответствии с их определением:

.
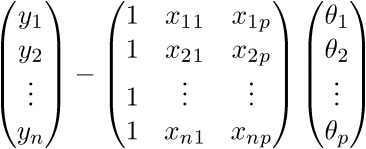Проверим размерность - для матрицы А она равна (n;p), а для вектора

- (p;1), а для вектора

- (n;1). В результате получим разницу двух векторов размерностью (n;1) -

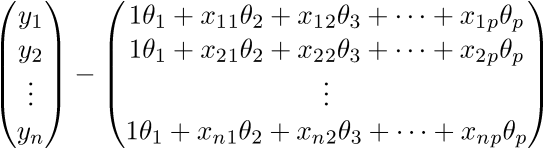
Сверимся с определением - по определению выходит, что каждая строка правой матрицы равна

. Запишем далее:

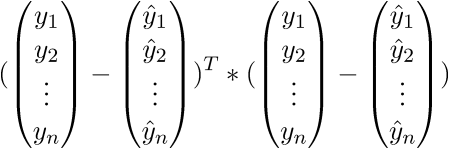
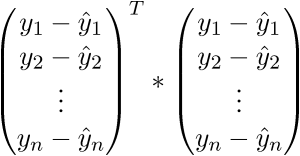
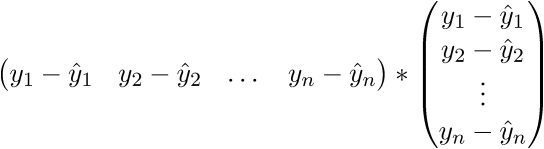
В итоге последняя строка и есть сумма квадратов длин, как нам и нужно. Каждый раз, конечно же, такие фокусы в уме проворачивать довольно долго, но к векторной нотации можно привыкнуть быстро. У этого есть и плюс для программиста - удобней работать и портировать код для GPU, где ехал вектор через вектор. Я как-то портировал генерацию шума Перлина на GPU и примерное понимание векторной нотации неплохо облегчило работу. Есть и минус - придется постоянно лезть в интернет, чтобы вспомнить тождества и правила линейной алгебры. После доказательства верности векторной нотации перейдем к дальнейшим преобразованиям:

Здесь использованы свойства транспонирования матриц - а именно транспонирование суммы и произведения. А также тот факт, что выражения

есть константа. Доказать можно взяв размерность матриц из их определения и посчитав размерность выражения после всех умножений:

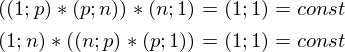
Константу можно представить как симметричную матрицу, следовательно:

После преобразований и раскрытия скобок, приходит время решить-таки поставленную задачу - найти минимум данного выражения, учитывая

. Минимум находится весьма буднично - приравнивая первый дифференциал по

к нулю. По-хорошему, нужно сначала доказать, что этот минимум вообще существует, предлагаю доказательство опустить и подсмотреть его в литературе самостоятельно. Интуитивно и так понятно, что функция квадратичная - парабола, и минимум у нее есть.

Итак,

Часть

называют псевдообратной матрицей.

Теперь в наличии все нужные формулы. Последовательность действий такая:
1) Сгенерировать набор экспериментальных данных.
2) Создать матрицу A.
3) Найти псевдообратную матрицу

.
4) Найти

После этого задача будет решена - у нас в распоряжении будут параметры прямой линии, наилучшим образом обобщающей экспериментальные данные. Иначе, у нас окажутся параметры для прямой, наилучшим образом выражающей линейную зависимость одной переменной от другой - именно это и требовалось.

generate_linear.py

import numpy as np import matplotlib.pyplot as plt  TOTAL = 200 STEP = 0.25   def func(x):     return 0.2 * x + 3  def prediction(theta):     return theta[0] + theta[1] * x   def generate_sample(total=TOTAL):     x = 0     while x < total * STEP:         yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8)         x += STEP   X = np.arange(0, TOTAL * STEP, STEP) Y = np.array([y for y in generate_sample(TOTAL)]) Y_real = np.array([func(x) for x in X])   A = np.empty((TOTAL, 2)) A[:, 0] = 1 A[:, 1] = X  theta = np.linalg.pinv(A).dot(Y) print(theta) Y_prediction = A.dot(theta)  error = np.abs(Y_real - Y_prediction) print("Error sum:", sum(error))  plt.plot(X, Y, 'bo') plt.plot(X, Y_real, 'g', linewidth=2.0) plt.plot(X, Y_prediction, 'r', linewidth=2.0) plt.show()

И результаты:

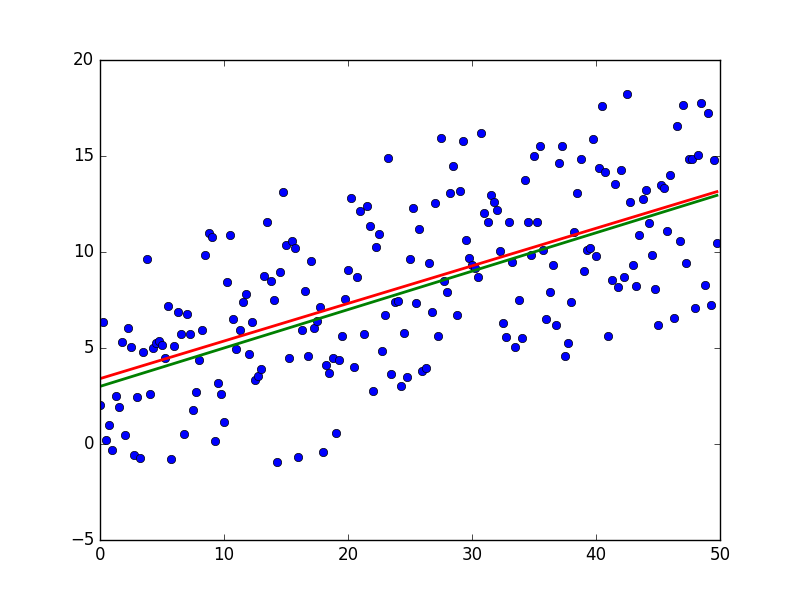
Красная линия была предсказана и почти совпадает с зеленой «базой». Параметры в моем запуске равны: [3.40470411, 0.19575733]. Попробовать предсказать значения не выйдет, потому что пока неизвестно распределение ошибок модели. Все, что можно сделать, так это проверить, правда ли для данного случая МНК будет подходящим и лучшим методом для обобщения. Условий три:
1) Мат ожидание ошибок равно нулю.
2) Дисперсия ошибок - постоянная величина.
3) Отсутствует корреляция ошибок в разных измерениях. Ковариация равна нулю.

Для этого я дополнил пример вычислением необходимых величин и провел измерения дважды:

generate_linear.py

import numpy as np import matplotlib.pyplot as plt  TOTAL = 200 STEP = 0.25   def func(x):     return 0.2 * x + 3   def prediction(theta):     return theta[0] + theta[1] * x   def generate_sample(total=TOTAL):     x = 0     while x < total * STEP:         yield func(x) + np.random.uniform(-1, 1) * np.random.uniform(2, 8)         x += STEP   X = np.arange(0, TOTAL * STEP, STEP) Y = np.array([y for y in generate_sample(TOTAL)]) Y_real = np.array([func(x) for x in X])   A = np.empty((TOTAL, 2)) A[:, 0] = 1 A[:, 1] = X  theta = np.linalg.pinv(A).dot(Y) print(theta) Y_prediction = A.dot(theta)  error = Y - Y_prediction error_squared = error ** 2 M = sum(error) / len(error) M_squared = M ** 2 D = sum([sq - M_squared for sq in error_squared]) / len(error)  print("M:", M) print("D:", D)  plt.plot(X, Y, 'bo') plt.plot(X, Y_real, 'g', linewidth=2.0) plt.plot(X, Y_prediction, 'r', linewidth=2.0) plt.show()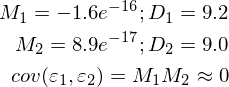

Неидеально, но все без обмана работает так, как и ожидалось.

Следующая часть.

Полный список библиотек для запуска примеров: numpy, matplotlib, requests.
Материалы, использованные в статье - https://github.com/m9psy/neural_nework_habr_guide

Источник: habrahabr.ru

Математика для искусственных нейронных сетей для новичков, часть 1 - линейная регрессия

Комментарии: