Успехи Google в квантовых вычислениях с точки зрения программирования

Успехи, о которых идет речь - демонстрация условий, в которых квантовый компьютер D-Wave быстрее обычного CPU в 100 миллионов раз. Новость об этом пролетала и тут, и вообще везде.

Что же это значит для простых смертных? Надо ли вовсю переключаться на программирование на квантовых компьютерах? Что там вообще за программирование?
Мне стало любопытно, и я немного почитал про детали (сама научная статья - тут). Как всегда, кратко рассказываю свое понимание.

Disclaimer: пост написан на основе изрядно отредактированных логов чата closedcircles.com, отсюда и стиль изложения, и наличие уточняющих вопросов.

Для начала, немного бэкграунда - что такое процессоры D-Wave.
Делать универсальный квантовый компьютер - это очень сложно и непонятно как, поэтому D-Wave делают очень узко-специализированное железо, которое решает исключительно задачу quantum annealing.

Что такое вообще annealing?

Это задача оптимизации вот такого выражения:

Есть N бинарных переменных s_i, они принимают значения -1 или +1. Можно задавать вещественные коэффициенты h_i и J_ij.
annealing - это минимизация E для всех возможных значений бинарных переменных (при фиксированных коэффициентах).

а чем управляем в итоге? h_i,J_ij?
Мы можем задавать их извне, да.
что инпут, а что аутпут? если мы задаем h_i, J_ij извне, то эта махина находит набор s_i при котором E минимальна или что?
Да, именно так.

Далее, надо понимать, что квантовый процесс не гарантирует нахождения глобального минимума, он с некой вероятностью находит значение, которое сколько-то близко к нему.

Какие практические задачи можно решать таким образом?

Пример в Гугловской статье - так называемый Number Partitioning Problem (NPP).
Классическая задача - есть набор из N положительных чисел, нужно разделить их на две кучи, чтобы суммы чисел в каждой куче были как можно ближе друг к другу.

Даже такая простая, казалось бы, задача - NP-hard и все эти дела, но ее довольно просто выразить как annealing.

Пусть бинарная переменная - это флаг принадлежности к какой-то куче.
Тогда нужно минимизировать:

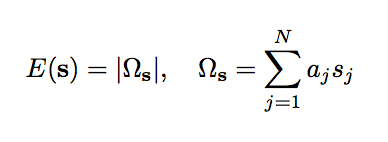
Минимизация модуля - это то же самое, что минимизация квадрата.

не понимаю связку между первой формулой и задачей разделения на кучи
Вот я расписал подробней:

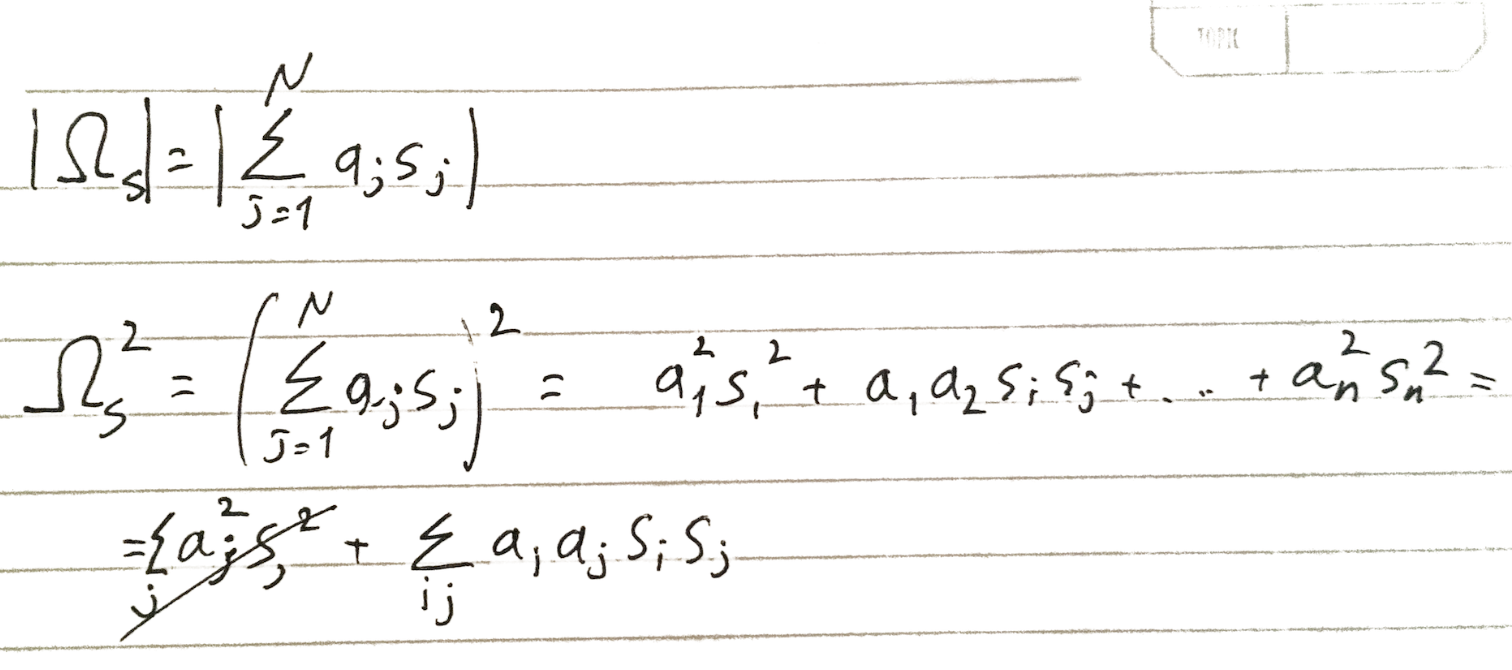
Как решаются такие задачи сейчас, на CPU?

Один из простых и все еще часто использующихся на практике методов - simulated annealing. Википедия пишет про него достаточно прилично - https://en.wikipedia.org/wiki/Simulated_annealing

Идея в том, чтобы начать с какого-то случайного состояния бинарных переменных и на каждом шаге их случайно флипать.
Если мы в результате флипа получили результат лучше - берем его. Если же нет, то берем или нет с некой вероятностью.
Вероятность зависит от разницы между новым и старым значением энергии и от так называемой "температуры" - еще одного параметра оптимизации, такого что в начале процесса температура большая, а чем дальше, тем меньше. За счет этого вероятностного процесса simulated annealing может вылезать из локальных минимумов. Разумеется, его можно проводить несколько раз, делать рестарты итд итп.
В нем нет никаких эвристик и можно управлять только "температурным режимом".

Какие ограничения у D-Wave на практике?

В последней версии D-Wave около тысячи кубитов (это то самое количество бинарных переменных в задаче).
Но есть некоторые детали!

• Первая: вот эти J_ij между двумя s_i и s_j (они еще называются couplings) требуют связи между отдельными кубитами, т.е. чтобы между двумя параметрами был ненулевой коэффициент J_ij - эти кубиты должны быть связаны.
  В NPP, например, связан каждый кубит с каждым, так как все J_ij ненулевые
  В D-Wave каждый кубит может быть связан (барабанная дробь) с ~10 другими, причем не с любыми, а заданными заранее.

  
  
• Вторая: с какой точностью можно задавать эти J_ij
  В D-Wave эта точность (снова дробь) - 4 бита.
  Напомню, что в NPP J_ij = a_i*a_j, т.е. для a_i остается 2 бита, лол.

На всякий случай, русским языком - сложно придумать практическую задачу, которую можно решать на этом всем добре.

И вот мужики в Гугле стараются придумать очень теоретическую задачу, которая бы максимально хорошо ложилась на эту архитектуру.

Почему вообще квантовый компьютер может быть эффективнее?

Если у нашего пространства много больших гор и впадин между ними...

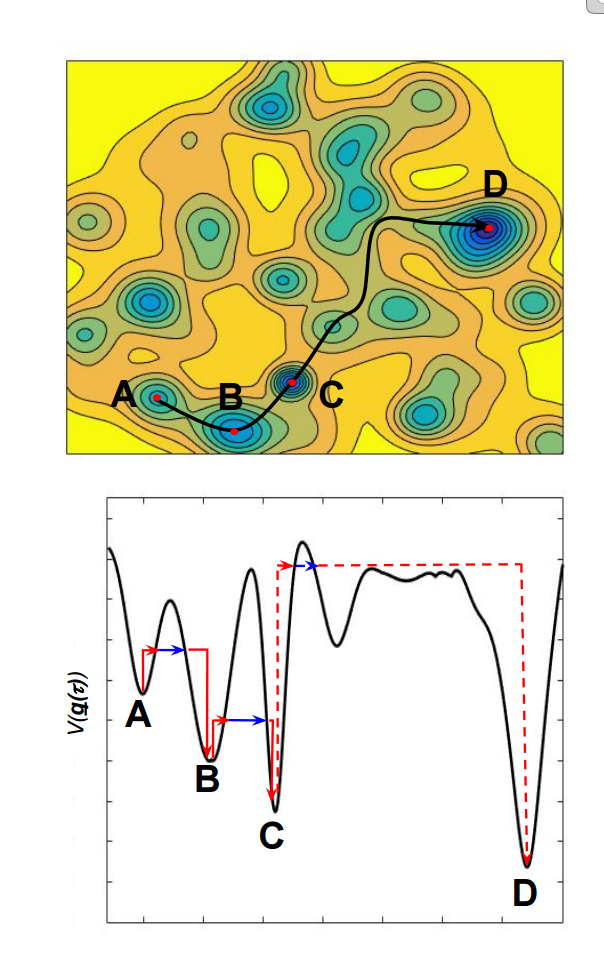То алгоритму нужно пройти через эти впадины в процессе оптимизации, и в отличие от simulated annealing, квантовый компьютер может "туннелировать" между достаточно узкими разломами.
Т.е. simulated annealing должен увеличить энергию системы чтобы выбраться наверх холма, а квантовый копмьютер может "туннелировать" сквозь стену не увеличивая энергию системы. Отчего сойтись быстрее - "увеличивать энергию" означает более долгий случайный поиск.
Расстояние, на котором туннельный переход может произойти, определяется параметрами системы - температурой компьютера (эти все процессы становятся квантовыми при ~10K), конкретными деталями физического лейаута итд итп.
Посему, нужна задача где много вот узких переходов такой длины, чтобы она преодолевалась D-Wave.

Ну хорошо, каким образом конструируется эта "хорошая" задача?

Основной элемент из которого они такую задачу собирают:

Это 8 кубитов одного знака, и 8 кубитов другого знака. Каждый в группе из 8 кубитов соединен с остальными связью с отрицательным весом (т.е. для минимизации энергии все в группе из 8 должны быть одного знака).
Между некоторыми кубитами из первой и второй группы тоже есть связь, тоже с отрицательным знаком (но более слабая), и для нее то, что изначально группы разного знака - плохо.
В идеале, в системе все кубиты должны быть одного знака, что приводит к минимуму энергии. Но флипаньем одного или двух битов туда попасть нельзя - нужно флипнуть все биты в группе из 8, чтобы получить лучшее значение. Это и создает такие высокие (но короткие) барьеры на ландшафте.

то есть они создают вот такую "удачную" задачу с помощью этой специальной конфигурацией связи кубитов?
Ага
а какой "реальной" задаче это соответствует?
Никакой!
Это все еще задача в рамках annealing (c h_i и J_ij), но практической ценности у нее нет никакой и быть не может.

Потом они повторяют эту конфигурацию на всех 1000 кубитах согласно связям, прошитым в железе:

Таким образом конструируются задачи разных размеров, где надо флипать кусками по 8 кубитов.

В работе сравнивается скорость D-Wave на этой задаче с simulated annealing и еще одним алгоритмом, Quantum Monte Carlo.
Quantum Monte Carlo - это алгоритм не для квантового компьютера, который, насколько я понимаю, пытается решить интеграл, описывающий квантовое уравнение системы, методом Монте Карло.

Ну и вот они сравнивают SA и QMC на одном ядре CPU и quantum annealing на D-Wave для достижения той же точности результата (95% от оптимального, кажись). SA в их задаче для этого, например, нужно 10⁹ запусков.

И вот теперь наконец-то мы готовы понять главный график из статьи:

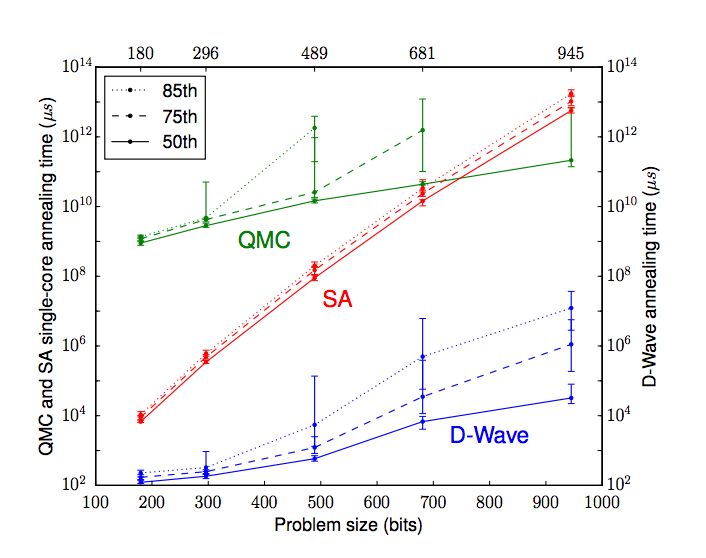
Это время выполнения задачи от количества бинарных переменных.

При максимальном размере задачи D-Wave действительно быстрее simulated annelaling в 10⁸ раз-
Но! Ассимптотически D-Wave не лучше QMC (то есть, и асимптотически лучше квантовый компьютер задачу не решает), но лучше SA.

у меня вот такой странный вопрос по этому графику, почему числа сверху такие неровные? это настоящий размер проблемы? как-то не делится на 8
Потому что в железе все несимметрично :)
Есть кубиты, у которых некоторых связей нет. На картинке полного графа видно, что есть некоторые выпадающие кластеры - где-то группа по 6, где-то 7.
Пикантности добавляет то, что у каждого экземпляра D-Wave этот граф немножко разный, потому что он зависит от yield defects.

Означает ли это что хотя бы эту вырожденную задачу квантовый компьютер решает лучше, чем обычный?

Нет! Лучше только если сравнивать с алгоритмами без эвристик.
Алгоритмы annealing с эвристиками (которые смотрят на связность графа итд) решают ее на одном CPU быстрее, чем D-Wave. Что неудивительно: задача на высоком уровне очень простая, если увидеть что надо флипать группами по 8.

Это подводит к нас к основной критике результата и неопределенности в светлом будущем.
Оптимистично можно надеяться, что в новом железе будет большая связность и большая точность коэффициентов coupling, что даст записывать более жизненные и сложные задачи (которые эвристиками решаться не будут).

Пессимистично можно сомневаться, получится ли вообще в ближайшем будущем построить что-то с такими параметрами, будет ли там вообще квантовый эффект, и будет ли у жизненных задач такой удачный ландшафт итд итп.

(больше подробностей, ада и угара здесь - http://www.scottaaronson.com/blog/?p=2555)

О чем еще можно сказать кроме этого...

• Good news - результат вроде бы доказывает, что какой-то квантовый процесс вообще в DWave происходит (это был предмет ожесточенных холиворов считай лет десять).
• Бороться за количество кубитов уже не нужно, нужно бороться за связи и точность.

Подытожив - можно расслабиться, внезапного рывка нет, это следующий шажок в освоении квантовых компьютеров, практическое применение еще далеко.
Можно продолжать писать на PHP и javascript.

Источник: geektimes.ru

Комментарии: