Математика цитрусовых

Предлагаю, если есть возможность, пойти на кухню, взять апельсин, очистить и проверить. Если лень или нет под рукой - воспользуемся скучной математикой: объем шара мы помним из школы. Пусть, скажем, толщина кожуры равна от радиуса, тогда , ; вычтем одно из другого, поделим объем кожуры на объем апельсина- получается, что кожуры что-то около 16%. Не так уж мало, кстати.

Как насчет апельсина в тысячемерном пространстве?

Пойти на кухню на этот раз не получится; подозреваю, что формулу наизусть тоже не все знают, но Википедия нам в помощь. Повторяем аналогичные вычисления, и с интересом обнаруживаем, что:
 

• во-первых, в тысячемерном гиперапельсине кожуры больше, чем мякоти
• а во-вторых, ее больше примерно в 246993291800602563115535632700000000000000 раз

То есть, каким бы странным и противоречивым это ни казалось, но почти весь объем гиперапельсина содержится в ничтожно тонком слое прямо под его поверхностью.

Начнем с этого, пожалуй.


 

Синопсис

Это вторая часть поста, где перед этим мы остановились на том, что нашли главный Грааль - апостериорную вероятность параметров модели. Вот она, еще раз, на всякий случай: . Вспомним еще раз, что - это параметры модели (веса нейронной сети, например), а - данные из датасета (я немного изменил нотацию, раньше вместо была , но тета нам понадобится попозже).

Так вот, апельсин - это как раз оно. Размеры этого posterior растут с такой же угрожающей быстротой, как и объем гиперапельсина; чем больше у нас параметров, тем «объемней» становится распределение. На самом деле, наверное, лучше представить даже не апельсин - давайте представим гору. В тысячемерном измерении. Да, я знаю, что это слегка непоследовательно, но энивей - вот, гора:
 

Эта всего в одномерном, правда. По заветам Хинтона, представить себе тысячемерную гору можно так: посмотреть на картинку выше и громко сказать «тысяча!» - или сколько там понадобится

Наш челлендж - это выяснить объем этой горы. При этом мы:
- не знаем, какой она формы (может быть какой угодно)
- (пока) владеем только одним способом измерения - стоя в точке, мы можем посчитать высоту до подножия (вероятность нахождения в этой точке)
- поверхность горы растет экспоненциально, когда растет - аналогично тому, как растет кожура гиперапельсина

Какой план?
 

План первый: сэмплинг

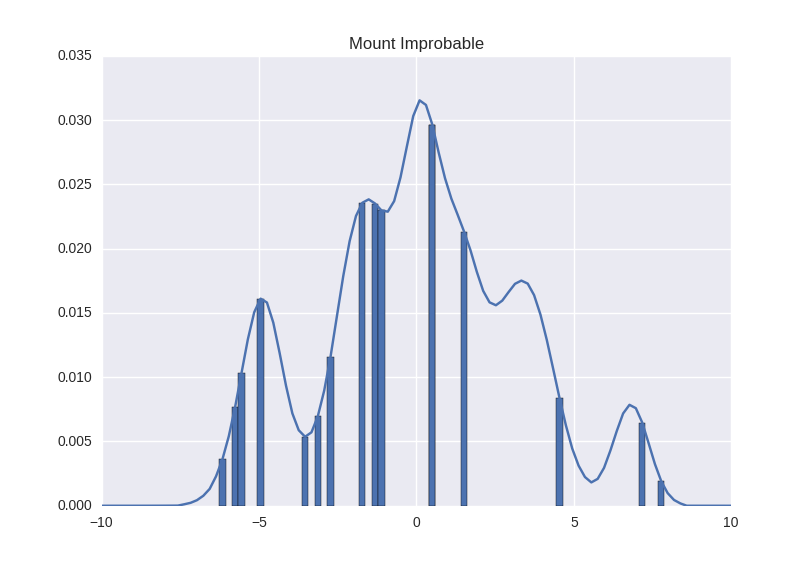
Нам, вообще говоря, совершенно не обязательно измерять гору прямо в каждой точке. Мы можем выбрать несколько случайных участков горы, сделать замеры и очертить по ним результат. Он будет не такой точный, зато нам придется сделать намного меньше измерений.
Можно довольно быстро заметить, что это мысль напрашивающаяся, но не очень нам поможет, когда наша многомерная гора начнет расти с увеличением числа измерений. Давайте вспомним, что поверхность горы равна <числу значений в одном измерении> в степени <числа измерений>. Сэмплинг поможет нам уменьшить основание степени - но показатель никуда не денется, и проблема все еще остается экспоненциальной.
 

План второй: аппроксимация

Главная проблема измерения горы не в том, что она большая (в плане числа измерений) - в конце концов, объем тысячемерного апельсина мы только что посчитали без особых затруднений по формуле из Википедии. Проблема в том, что для горы нет формулы. Мы не знаем аналитическое правило, по которому растет гора (в отличие от апельсина - он растет равномерно по все направлениям).

Ну ладно, а что если мы построим еще одну свою гору, которая будет похожа на искомую, но на этот раз с формулой? Примерно вот так:
 

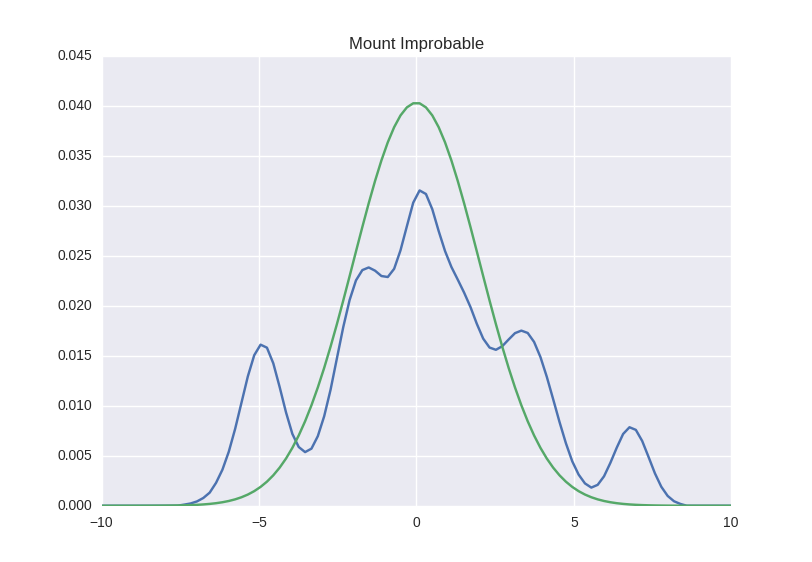
Ну- на самом деле черт его знает. Во-первых, пока не очень понятно, настолько точной может быть аппроксимация - на картинке она выглядит не очень-то. Во-вторых, мы пока не знаем, как это вообще сделать. Вот давайте для начала и разберемся.
 

Аппроксимация Лапласа

Еще раз нарисуем нашу теорему Байеса, только немного по-другому:
 

Я просто собрал произведение двух вероятностей справа от дроби в одну - так называемую совместную вероятность (и еще раз напомню, что мы слегка изменили нотацию на w вместо теты). Люди часто рассматривают это в таком смысле, что - наше «искомое» распределение, а - нормализующая константа, которая нужна, чтобы результат суммировался к одному. Так что давайте временно сфокусируемся на поиске .

Говорим «аппроксимация», вспоминаем ряды Тейлора. В соответствии с первым курсом матанализа любая функция раскладывается на бесконечную сумму опредленных полиномов. Запишем нашу функцию как , а раскладывать будем в некой точке , которая совпадает с максимумом распределения (мы не знаем, где оно, но это пока не важно). И заодно отпилим бесконечную сумму после слагаемого со степенью два:
 

(это прямо списанное один-в-один разложение в ряд Тейлора из википедии)

Теперь вспоминаем, что мы выбрали как точку максимума, а значит, производная в ней равна нулю. То есть второе слагаемое можно с чистой совестью выкинуть. Получаем
 

Ничего не напоминает? На самом деле у этой штуки такая же форма, как у логарифма от гауссиана. Чтобы это увидеть, можно записать
 

Чуть поменяем нотацию: мы хотели выбрать , а теперь пусть будет . Тогда , и получается, что наша искомая совместная вероятность может быть аппроксимирована гауссианом с центром в точке максимума и стандартным отклонением (обратная вторая производная в точке максимума или кривизна).

Если это было слишком много непонятных символов для одного раздела, просуммируем идею в трех коротких пунктах. Итак, если мы хотим найти наш объем горы, нам нужно:
- найти точку максимума
- измерить в ней кривизну (посчитать вторую производную; только внимание: производную по , а не )
- взять нормальную кривую с центром в точке максимума и стандартным отклонением - отрицательно-обратным к кривизне.

Искать точку максимума горы мы умеем и это гораздо легче, чем измерять ее всю. Собственно, а давайте применим магию к той же байесовской регрессии, с которой мы возились в прошлом посте!

Точку максимума мы искали в конце прошлого поста - это центр «байесовского пучка», «самая горячая линия» и т.д. Я, на всякий случай, еще раз приведу, как ее найти, но спрячу под спойлер, чтобы не пугать людей формулами:
 

Заголовок спойлера

Производную по можно посчитать аналитически, но поскольку я ужасный лентяй, я лучше забью все это в питон и пусть aurograd сделает работу за меня.
 

# b и w мы нашли через градиентный спуск с регуляризацией, как в конце прошлого поста # просто запихаем их в один массив ext_w = np.hstack([b, w])  # дописываем к данным единичку слева # это все делается для того, чтобы ext_data.dot(ext_w) # равнялось data.dot(w) + b  ext_data = np.ones((data.shape[0], data.shape[1] + 1)) ext_data[:, 1:] = data  # наша функция log joint, по которой надо брать производную # я немного упростил ее и раскрыл логарифмы def log_joint(w):     regression_value = ext_data.dot(w)     return (         np.sum(-np.power(target - regression_value, 2.) / (2 * np.power(1., 2.))) +         np.sum(-np.power(w, 2.) / (2 * np.power(1., 2.)))     )  from autograd import elementwise_grad  second_grad_log_joint = elementwise_grad(elementwise_grad(log_joint))  mu = ext_w sigma = -1. / second_grad_log_joint(ext_w) cov = np.diag(sigma)  # готово, теперь у нас есть распределение # some_value = multivariate_normal.pdf(some_point, mu, cov)...  

Когда у нас есть распределение, нарисовать его - дело техники; пользуемся примерно тем же способом, что и в прошлой части поста с небольшой модификацией (сэмплим распределение в разном удалении от центра). Получаем вот такую симпатичную картинку:
 

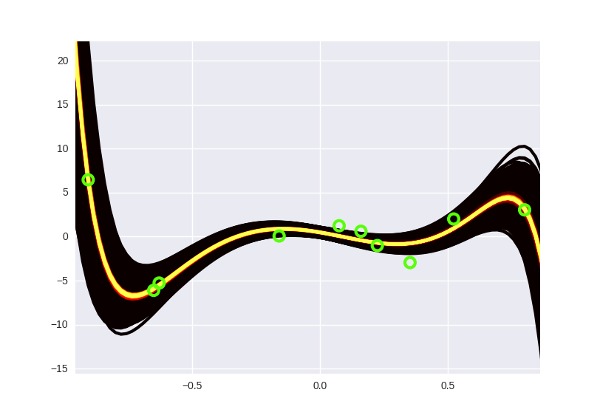
И между прочим, каждая кривая тут - полином 15 степени. Старая «брутфорсная» байесовская регрессия бы давно уже откинулась полежать на несколько лет компьютерного времени (там я кое-как выжимал пятую степень).

Аппроксимация Лапласа всем хороша - быстро, удобно, красиво - но одно плохо: она оценивается по точке максимума. Это как судить по всей горе, глядя на нее с вершины - при том, что мы не знаем, реально ли мы на вершине или застряли в локальном максимуме, и при том, что видно оттуда далеко не все (вдруг у нас на вершине все очень плоско и красиво, а под ней три километра сплошного обрыва?). В общем, придумали ее для нейронных сетей, как можно догадаться, не во времена Лапласа, а вовсе даже в 1991-м, но с тех пор она мир особо не завоевала. Так что давайте посмотрим на что-нибудь более модное и красивое.
 

Bayes by backprop: начало

Наконец мы добрались до того самого метода из заглавной статьи DeepMind. Авторы назвали его Bayes by backprop - удачи с переводом на русский язык, ага. Обратное байесораспространение?

Отправная точка здесь такая: представим, что у нас какая-то аппроксимация (вот где нам пригодился символ теты - это будут наши параметры аппроксимационного распределения), и пусть она будет какой-нибудь простой формы, тоже Гауссовой, скажем. Трюк вот в чем: попробуем записать выражение какой-нибудь «дистанции» от нашей аппроксимации до оригинальной горы, и минимизировать эту дистанцию. Поскольку обе величины - распределения вероятностей, заюзаем штуку, которую специально придумали для сравнения распределений: расстояние Кульбака-Лейблера. На самом деле это только звучит слегка страшно, а так это просто вот что:
 

Если внимательно посмореть на интеграл, то становится понятно, что он выглядит как матожидание - под интегралом какая-то штука, умноженная на , а интеграл взят по . Тогда можно записать его так:
 

Едем дальше: в знаменателе у нас стоит , а мы знаем, что по теореме Байеса оно равно . Засунем это в формулу повыше и заметим, что под матожиданием оказывается - которое не зависит от , и мы можем его из-под ожидания вынести:

Это мы сделали очень крутую вещь. Потому что если вы не забыли, вся эта штука равна разности аппроксимации и нашей горы. Управляемым параметром здесь является , и мы хотим подстроить ее так, чтобы разности оказалась минимальной. Так вот, в процессе этой минимизации нам не надо беспокоиться о
- потому что оно не зависит от . А это, между прочим, был главный проблемный компонент нашего posterior - чтобы его посчитать, нам как раз и приходилось обойти все точки горы и сложить их вместе (потому что , сумма по всем , и его по-другому особенно никак не получить).

Однако, едем дальше. Нас интересует поиск минимума того, что осталось:
 

Как мы обычно ищем минимумы? Ну, мы берем производную и делаем градиентный спуск. Есть идеи, как взять производную от этой фигни? У меня пока что-то не очень.
 

Bayes by backprop: продолжение

Тут наступает часть, в которую я так и не смог интуитивно въехать, поэтому придется сцепить зубы и следить за математикой. Часть, которая позволяет нам взять производную, называется reparameterization trick, и состоит из следующих шагов:
 

1. Допустим, взяли мы какую-то случайную величину . Ничего мы про нее не знаем, кроме того, что выбрана она так, что . Вот такое у нее свойство, и все пока про нее.
2. Вообще говоря, производная от матожидания не так страшна, как кажется: это всего лишь производная от интеграла, то есть, грубо говоря, от суммы, где суммирование идет по . Само по себе не страшно, но нудно, потому что мы опять возвращаемся к проблеме под названием «собрать в кучу все точки бесконечно растущего ». Давайте представим в общем виде, что под матожиданием какая-то функция , и напишем нашу производную:

Ничего особенного мы не сделали - просто раскрыли матожидание по определению из википедии, записали его опять в виде интеграла. Но погодите, видите в конце? Мы только что сказали, что оно равно . И-иии-
 

Теперь наш интеграл делается по эпсилону, а значит, мы можем загнать производную по
под знак интеграла.
 

Вот он reparametrization trick: была у нас производная от матожидания, стало матожидание от производной. Круто? Подозреваю, что если вы еще следуете за моими медленными ведениями пальцем по строчкам, то вам не очень круто, и может быть, даже не очень понятно, что изменилось - один фиг нам нужно интегрировать по , чего мы добились вообще?

Суть в том, что теперь мы можем аппроксимировать этот интеграл в нескольких точках (сэмплами). А раньше не могли. Раньше производную нужно было взять от всей суммы: сначала собрать вместе кучу точек, а потом ее дифференцировать, и там любая неточность при собирании могла увести нас при дифференцировании далеко-далеко не в ту сторону. А теперь мы можем дифференцировать в точках, а уже потом суммировать результаты - и значит, вполне можем обойтись частичной суммой.

Вот такие суровые порядки в мире приближенного вывода: тут нам нужны аппроксимации, чтобы вычислить производную, даже не само posterior-распределение. Ну ничего, мы почти у цели.
 

Bayes by backprop: алгоритм

До сих пор мы относились к как к абстрактным «параметрам»: пришло время их уточнить. Пусть наша аппроксимация будет гауссовой: тогда представим в виде - среднего значения, и - стандартного отклонения. Еще нам нужно определиться с - давайте сделаем его гауссовой случайной величиной с центром в нуле и стандартным отклонением 1, т.е. . Тогда чтобы выполнялось условия для репараметризации, пусть
 

( здесь означает поэлементное умножение). Для меня, правда, тут не очень очевидно, почему при этом (если кто-нибудь сможет на пальцах объяснить в комментах - буду очень благодарен), но примем этот кусочек статьи на веру.

Итого наше обратное байесораспространение состоит из следующих шагов:
 

1. Начинаем со случайных и для каждого веса нейронной сети (или коэффициента регрессии)
2. Сэмплим немного из
3. Получаем из него
4. Вспоминаем нашу функцию дистанции между «истинной горой» и аппроксимацией. Мы однажды обозначали ее как , но по-хорошему это . Я ее ниже все равно напишу как , так проще (держим в голове, что ).
5. Считаем производную по . Это будет:
    

   

   
   (откуда плюс? потому что - функция от двух переменных, и обе зависят от )
6. Считаем производную по :
    

   

7. Есть производные - дело фигурально в шляпе. Дальше старый добрый градиентный спуск:
    

   

Какие-нибудь результаты

Не знаю как вам, а мне уже надоел этот черно-желтый пучок, так что давайте пропустим эту обязательную стадию и сделаем что-нибудь более похожее на нейронную сеть. Авторы оригинальной статьи получили симпатичные результаты на MNIST-цифрах без всяких дополнительных извращений типа использования сверточных сетей - давайте попробуем подобраться к ним. И пожалуй, настало время отложить симпатичный autograd в сторонку и вооружиться чем-нибудь потяжелее вроде Theano. Дальше будет немного Theano-специфичного кода, так что если вы в нем не ориентируетесь - смело пролистывайте.

Достаем данные:
 

from sklearn.datasets import fetch_mldata from sklearn.cross_validation import train_test_split from sklearn import preprocessing  import numpy as np  mnist = fetch_mldata('MNIST original') N = 5000  data = np.float32(mnist.data[:]) / 255. idx = np.random.choice(data.shape[0], N) data = data[idx] target = np.int32(mnist.target[idx]).reshape(N, 1)  train_idx, test_idx = train_test_split(np.array(range(N)), test_size=0.05) train_data, test_data = data[train_idx], data[test_idx] train_target, test_target = target[train_idx], target[test_idx]  train_target = np.float32(preprocessing.OneHotEncoder(sparse=False).fit_transform(train_target)) 

Объявляем параметры. Тут применим небольшой трюк, про который есть в статье, но я сознательно не рассказывал. Дело вот в чем: для кажого веса сети у нас есть два параметра - мю и сигма, так? Небольшая проблемка может возникнуть с тем, что сигма должна всегда быть больше нуля (это стандартное отклонение гауссиана, которое отрицательным не может быть по определению). Во-первых, как ее инициализировать? Ну, можно взять случайные числа от чего-то очень близкого к нулю (типа 0.0001) до единицы. Во-вторых, а не заедет ли она в процессе градиетного спуска ниже нуля? Ну, вроде не должна, хотя за счет всяких арифметических неточностей после запятой может и. В общем, авторы предложили решить это элегантно - мы заменим сигму на логарифм от сигмы, и сделаем соответствующую поправку в формулу весов:

(зачем тут под логарифмом +1? видимо, с той же целью - чтобы случайно не взять логарифм от нуля).

А, ну и раньше мы все время говорили о весах как о , но у нас в нейронных сетях часто своя номенклатура - нулевой вес, там называется (bias). Не будем нарушать соглашение. Итак:
 

def init(shape):     return np.asarray(         np.random.normal(0, 0.05, size=shape),         dtype=theano.config.floatX     )  n_input = train_data.shape[1]  # L1 n_hidden_1 = 200 W1_mu = theano.shared(value=init((n_input, n_hidden_1))) W1_logsigma = theano.shared(value=init((n_input, n_hidden_1))) b1_mu = theano.shared(value=init((n_hidden_1,))) b1_logsigma = theano.shared(value=init((n_hidden_1,)))  # L2 n_hidden_2 = 200 W2_mu = theano.shared(value=init((n_hidden_1, n_hidden_2))) W2_logsigma = theano.shared(value=init((n_hidden_1, n_hidden_2))) b2_mu = theano.shared(value=init((n_hidden_2,))) b2_logsigma = theano.shared(value=init((n_hidden_2,)))  # L3 n_output = 10 W3_mu = theano.shared(value=init((n_hidden_2, n_output))) W3_logsigma = theano.shared(value=init((n_hidden_2, n_output))) b3_mu = theano.shared(value=init((n_output,))) b3_logsigma = theano.shared(value=init((n_output,))) 

Эту логсигму надо как-то уметь запихивать в формулу нормального распределения, поэтому сделаем под нее свою функцию. Заодно и обычную объявим:
 

def log_gaussian(x, mu, sigma):     return -0.5 * np.log(2 * np.pi) - T.log(T.abs_(sigma)) - (x - mu) ** 2 / (2 * sigma ** 2)   def log_gaussian_logsigma(x, mu, logsigma):     return -0.5 * np.log(2 * np.pi) - logsigma / 2. - (x - mu) ** 2 / (2. * T.exp(logsigma)) 

Настало время оценить наши вероятности. Делаем мы это, как и собирались раньше, сэмплингом - то есть крутимся в цикле, на каждой итерации получаем рандомно-инициализирующий эпсилон, превращаем его в веса и собираем вместе. Вообще для циклов в Theano есть scan, но: 1) его явно разрабатывал коллектив маниакальных инквизиторов с целью как можно сильнее сломать мозг пользователю и 2) для небольшого числа итераций нам и обычный цикл сгодится. Итого:
 

n_samples = 10 log_pw, log_qw, log_likelihood = 0., 0., 0. for _ in xrange(n_samples): epsilon_w1 = get_random((n_input, n_hidden_1), avg=0., std=sigma_prior) epsilon_b1 = get_random((n_hidden_1,), avg=0., std=sigma_prior) W1 = W1_mu + T.log(1. + T.exp(W1_logsigma)) * epsilon_w1 b1 = b1_mu + T.log(1. + T.exp(b1_logsigma)) * epsilon_b1 epsilon_w2 = get_random((n_hidden_1, n_hidden_2), avg=0., std=sigma_prior) epsilon_b2 = get_random((n_hidden_2,), avg=0., std=sigma_prior) W2 = W2_mu + T.log(1. + T.exp(W2_logsigma)) * epsilon_w2 b2 = b2_mu + T.log(1. + T.exp(b2_logsigma)) * epsilon_b2 epsilon_w3 = get_random((n_hidden_2, n_output), avg=0., std=sigma_prior) epsilon_b3 = get_random((n_output,), avg=0., std=sigma_prior) W3 = W3_mu + T.log(1. + T.exp(W3_logsigma)) * epsilon_w3 b3 = b3_mu + T.log(1. + T.exp(b3_logsigma)) * epsilon_b3 a1 = nonlinearity(T.dot(x, W1) + b1) a2 = nonlinearity(T.dot(a1, W2) + b2) h = T.nnet.softmax(nonlinearity(T.dot(a2, W3) + b3)) sample_log_pw, sample_log_qw, sample_log_likelihood = 0., 0., 0. for W, b, W_mu, W_logsigma, b_mu, b_logsigma in [(W1, b1, W1_mu, W1_logsigma, b1_mu, b1_logsigma), (W2, b2, W2_mu, W2_logsigma, b2_mu, b2_logsigma), (W3, b3, W3_mu, W3_logsigma, b3_mu, b3_logsigma)]: # first weight prior log_pw += log_gaussian(W, 0., sigma_prior).sum() log_pw += log_gaussian(b, 0., sigma_prior).sum() # then approximation log_qw += log_gaussian_logsigma(W, W_mu, W_logsigma * 2).sum() log_qw += log_gaussian_logsigma(b, b_mu, b_logsigma * 2).sum() # then the likelihood log_likelihood += log_gaussian(y, h, sigma_prior).sum() log_qw /= n_samples log_pw /= n_samples log_likelihood /= n_samples

Фух. Теперь собираем objective. Где-то в этом месте в посте должна быть пауза на две недели, потому что objective, который предлагается в статье (что-то типа

(log_qw - log_pw - log_likelihood / M).sum()) у меня нифига не работал и выдавал очень плохие результаты. Потом в какой-то момент я сообразил дочитать статью до конца и обнаружил, что авторы советуют работать с минибатчами и усреднять objective определенным образом. Точнее даже вот таким:
 

objective = ((1. / n_batches) * (log_qw - log_pw) - log_likelihood).sum() / batch_size 

Заодно советовали использовать оптимизатор Adam вместо обычного градиентного спуска. Никогда в жизни им не пользовался, поэтому удержимся от соблазна написать его самостоятельно и воспользуемся готовым.
 

from lasagne.updates import adam  all_params = [     W1_mu, W1_logsigma, b1_mu, b1_logsigma,     W2_mu, W2_logsigma, b2_mu, b2_logsigma,     W3_mu, W3_logsigma, b3_mu, b3_logsigma ] updates = adam(objective, all_params, learning_rate=0.001) 

Ну а дальше все стандартно - train-функция и идем непосредственно обучаться. Весь код можно посмотреть тут. Сильно больших процентов точности там не получается, правда, но и то хлеб.
 

epoch 0 cost 6.83701634889 Accuracy 0.764 epoch 1 cost -73.3193287832 Accuracy 0.876 epoch 2 cost -89.2973277879 Accuracy 0.9 epoch 3 cost -95.9793596695 Accuracy 0.924 epoch 4 cost -100.416764595 Accuracy 0.924 epoch 5 cost -104.000705026 Accuracy 0.928 epoch 6 cost -107.166556952 Accuracy 0.936 epoch 7 cost -110.469004896 Accuracy 0.928 epoch 8 cost -112.143595876 Accuracy 0.94 epoch 9 cost -113.680839646 Accuracy 0.948 

Оставлю ссылку на статью, на всякий случай, еще раз, потому что там много еще всего интересного: как перейти от аппроксимации гауссианом к чему-то более сложному, или например, как использовать эту штуку в reinforcement learning (ну это же DeepMind, в конце концов).
 

Q&A

1. Там в статье и вообще везде часто используется слово «вариационный», а в посте про это ничего не сказано.
   
   Тут я, к стыду своему, просто постеснялся: в свое время в школе у меня не было вариационного исчисления, и я слегка остерегаюсь использовать незнакомые термины, тем более что можно и без них обойтись. Но вообще да: про подход в целом можно почитать в разделе вариационных Байесовских методов. На пальцах, насколько я понимаю, смысл названия такой: вариационное исчисление работает с функциями так же, как обычный матанализ - с числами. То есть там, где мы в школе искали точку, в которой достигался минимум функции, здесь мы ищем функцию (ту самую ), которая минимизирует KL-дивергенцию, например.
2. В прошлом посте был вопрос - а при чем тут dropout и вообще, связан ли он как-то со всем этим делом?
   
   Еще как. Дропаут можно рассматривать как дешевую версию байесовскости, которая зато очень простая. Идея строится все на той же аналогии с ансамблями, про которую я упоминал в конце прошлого поста: вот представьте, что у вас есть нейронная сеть. Теперь представьте, что вы берете ее, случайно отрываете ей несколько нейронов, и откладываете в сторонку. После ~1000 таких операций вы получаете ансамбль из тысячи сетей, где каждая слегка отличается друг от друга случайным образом. Мы усредняем их предсказания, и получаем, что случайные отклонения местами компенсируют друг друга и дают актуальные предсказания. Теперь представьте, что у вас есть байесовская сеть, и вы тысячу раз достаете набор ее весов из неопределенности, и получаете такой же ансамбль слегка отличающихся друг от друга сетей.
   
   Чем байесовский подход круче - он позволяет использовать эту рандомность контролируемым образом. Вот посмотрите еще раз на картинку:
   
   
   
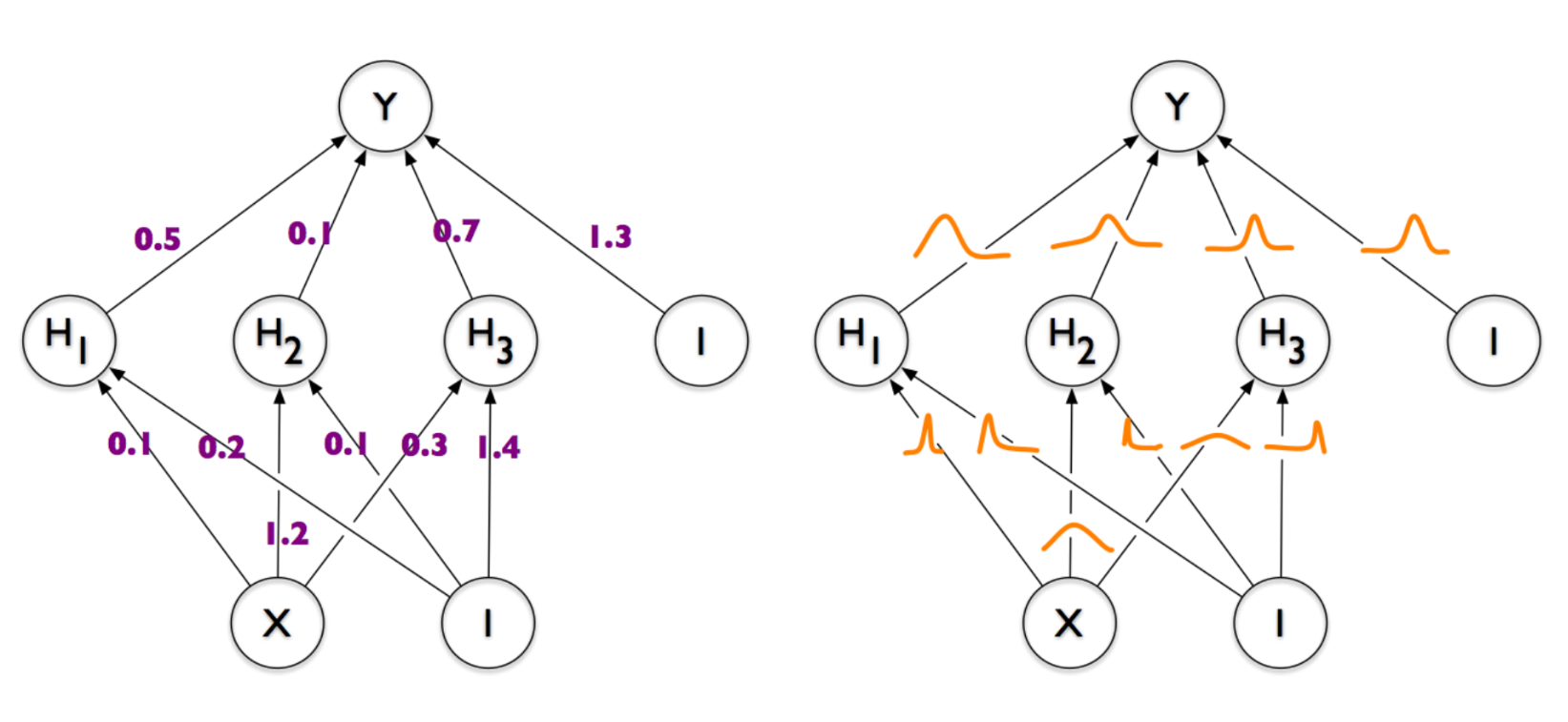
   Каждый вес тут - случайная величина, но случайности эти разные. Где-то пик гауссианы сильно сдвинут влево, где-то вправо, где-то он в центре и имеет большую дисперсию. Предположительно в результате обучения каждый вес приобретает такую форму, которая наиболее подходит для выполнения сетью своей задачи. То есть если у нас есть какой-то очень важный вес, например, который должен быть строго равен вон тому-то, иначе вся сеть поломается, то при сэмплинге весов этот нейрон, скорее вcего, останется на месте. В случае с дропаутом мы просто равномерно-случайным образом отключаем веса, и запросто можем этот важный вес грохнуть. Дропаут ничего не знает о его «важности», для него все веса одинаковые. На практике это выражается в том, что димпайндовская сеть дает лучшие результаты, чем сеть с дропаутом, хоть и ненамного.
   
   Чем дропаут круче - это тем, что он очень простой, конечно.
3. Нафига вы вообще всем этим занимаетесь? Нейронные сети, предположительно, должны быть построены по образу и подобию штуковин у нас в голове. Там-то уж явно нет никаких гауссовых весов, зато есть много всего, что вы, машинлернеры, вчистую игнорируете (временной фактор, дискретные спайки и прочая биология). Выкиньте свои учебники по терверу и покайтесь!
   
   Хороший способ, которым мне нравится думать про нейронные сети, включает в себя такую историческую цепочку:
    
   • люди в какой-то момент задумались, что всякое мышление и вообще процессы в мире можно организовать по цепочкам «причина-следствие». Что-то произошло, потом произошло что-то еще, и это все вместе повлияло на что-то третье.
   • они начали строить такие символьные модели типа обычных байесовских сетей (не путать с сабжем), и поняли, что такие модели могут отвечать на всякие самые разные вопросы («если на улице солнечно и Себастьян счастлив, какая вероятность того, что Себастьяну сегодня выдали зарплату?») и отвечать довольно хорошо.
   • но в такие модели все переменные приходилось вбивать руками. В какой-то момент пришел коннекционизм и сказал: а давайте просто насоздаем кучу случайных переменных и свяжем их все друг с другом, а потом как-то обучим эту модель, чтобы она нормально работала.
   
   И вот так получились в том числе нейронные сети. Они на самом деле не должны быть такими, как мокрые биологические сети у нас в голове. Они делаются для того, чтобы там где-то у себя внутри получить правильную комбинацию причин и следствий в виде нейронов, которые втыкаются один в другой. Каждый нейрон внутри - это потенциальный «фактор», какая-то переменная, ответственная за что-то, и байесовская магия помогает сделать эти факторы более полезными.
   
   Что делает каждый нейрон внутри нашей головы? Да черт его знает. Очень может быть, что и ничего особенного.
4. Что еще есть по этой теме?
   
   О, много всего:
    
   • Вариационные автоэнкодеры - по-моему, чуть ли не самая популярная модель, и по-хорошему, надо было начать с нее, но уж очень мне понравилась эта.
   • На самом деле если заглянуть чуть глубже в историю машинного обучения, то вариационные аппроксимации там торчат из каждого утюга. Скажем, в deep Bolztmann machine (которые особо нигде не используются, кажется, но энивей), или в штуке под названием NADE, которая переделывает машину Больцмана на языке обратного распространения ошибки.
   • Variational black box - я даже не знаю, что это, потому что наткнулся на него только дописывая пост, но мне уже нравится название и обещание во введении.
   • DRAW, до которой я никак не доберусь и которая выглядит просто потрясающе: рекуррентная сеть с attention-механизмом, которая может рисовать циферки как карандашом.
   • штука под названием Ladder Network, которая объединяет supervised и unsupervised learning

Комментарии: