Оптимизация планирования доставки грузов. Алгоритм кластеризации k-means (метод K-средних).

Что такое кластеризация? Это объединение объектов в непересекающиеся группы, называемые кластерами, на основе близости значений их атрибутов (признаков). В результате в каждом кластере будут находиться объекты, похожие по своим свойствам друг на друга и отличающиеся от тех, которые расположены в других кластерах. При этом, чем больше подобие объектов внутри кластера и чем сильнее их непохожесть на объекты в других кластерах, тем лучше кластеризация.

Взгляните на фото .. так выглядит бардак..  после того как дочка поиграла и бросила на полу в своей комнате вещи. При виде такого безобразия, ей тут же прилетает задача прибраться в комнате, а это значит что ей нужно произвести кластеризацию вещей по признаку, то есть игрушки отнести в одну группу, книжки- в другую, а карандаши  в третью и т.д., чтобы затем убрать все на свои места.

Признак, по которому мы собираем одни предметы в одну группу, а другие в другую, называется метрикой. Грубо говоря, метрика - это просто способ отделить один предмет от другого. Самый распространненый вариант - это когда метрикой является расстояние.
Кластеризация (деление на кластеры) может быть и немного другой. Например, если поставить задачу разделить все вещи на четыре кучи (кластера), то при этом наверняка игрушки попадут в одну кучу с книжками или карандашами, т.е перемешаются. Такой метод называется алгоритм кластеризации К-средних, то есть мы заранее задаем количество кластеров, а алгоритм сам разделяет объекты на это количество.

Описание алгоритма кластеризации "для чайников"

Описание  алгоритма кластеризации

Пример работы алгоритма

Одно время были книжки из серии "для чайников", и там по-простому говорилось о "сложных материях". Попробую объяснить по-простому, как работает сам алгоритм кластеризации. Он итерационый, то есть повторяется несколько раз, пока не «сойдется». Сходимость в данном случае значит, что с каждой итерацией (повторением вычислений) мы все точнее приближаемся к правильному ответу. А «сошелся» в данном случае значит, что мы нашли правильный ответ или мы очень близко к нему (то есть нашлось число с небольшой погрешностью, на которую мы плюем и топчем ногами). 

В данном случае мы будем работать с точками на плоскости размером 20 на 20 (не важно даже каких единиц).  Например, дано 50 точек, расположенных случайным образом. Нужно распределить эти точки по кластерам алгоритмом К-средних (или K-means).

Действуем так:

Сначала случайным образом выставляем на этой же плоскости несколько центров кластеров, например 4. Центр кластера называется центроидом. Без начального положения центроидов не удастся запустить алгоритм (увидите, почему). Как их расставить - дело ваше, можно самостоятельно вводить координаты, можно применить еще какой-нибудь алгоритм. Далее начинается вычисление кластеров в цикле. Делается это так:

1. 1. Сначала мы «привязываем» каждую точку к тому центроиду, к которому она ближе, т.к. центроид является центром кластера, то можно сказать, что мы относим каждую точку к тому кластеру, к центру которого она ближе.
   2. Когда все точки привязаны и ни одна от нас не убежала, нужно пересчитать координаты центроидов. Для этого мысленно вписываем весь кластер в прямоугольник и ставим центроид туда, где пересекутся его диагонали (в середину, короче). Квадратики - это центры кластеров. Линии от точек до центров нужны просто для наглядности, чтобы сразу видеть, к какому центру принадлежит точка.
       
   3. Повторяем для нового центра действия с шага 1 до тех пор, пока центроиды не перестанут менять своего положения. Если они перестали менять положение, значит алгоритм сошелся и мы теперь крутые перцы. Кстати, как правило алгоритм сходится где-то за 2-6 итераций. Но в теории возможно, что алгоритм не сойдется вообще, поэтому на всякий случай нужно включить в него «защиту» - прервать его после например 30 итераций. Это гарантирует, что программа не зависнет.

Теперь для тех, кто все-таки добрался до этого места и не сбежал, приведу более строгое математическое описание метода и пример расчета.

Описание алгоритма кластеризации

Для выборки данных, содержащей n записей (объектов), задается число кластеров k , которое должно быть сформировано. Затем алгоритм разбивает все объекты выборки на k разделов (k < n), которые и представляют собой кластеры. 

Одним из наиболее простых и эффективных алгоритмов кластеризации является алгоритм k-means (Mac-Queen, 1967) или в русскоязычном варианте k-средних (от англ. mean - среднее значение). Он состоит из четырех шагов, но сначала задается число кластеров k, которое должно быть сформировано из объектов исходной выборки.

1. Случайным образом выбирается k записей исходной выборки, которые будут служить начальными центрами кластеров l. Такие начальные точки, из которых потом «вырастает» кластер, часто называют «семенами» (от англ. seeds - семена, посевы). Каждая такая запись будет представлять собой своего рода «эмбрион» кластера, состоящий только из одного элемента.

2. Для каждого центройда  вычислить расстояния  до всех точек

Ключевым моментом алгоритма k-means является вычисление на каждой итерации расстояния между записями и центрами кластеров, что необходимо для определения, к какому из кластеров принадлежит данная запись. Правило, по которому производится вычисление расстояния в многомерном пространстве признаков, называется метрикой. Наиболее часто в практических задачах кластеризации используются следующие метрики. 

• Евклидово расстояние или метрика L2

где  - наборы (векторы) значений признаков двух записей.

Поскольку множество точек, равноудаленных от некоторого центра при использовании евклидовой метрики будет образовывать сферу (или круг в двумерном случае), то и кластеры, полученные с использованием евклидова расстояния, также будут иметь форму, близкую к сферической.

• Расстояние Манхэттена (англ.: Manhattan distance) или метрика L1

 

Фактически это кратчайшее расстояние между двумя точками, пройденное по линиям, параллельным осям координатной системы (см рис. ниже).

 

Преимущество метрики L1 заключается в том, что ее использование позволяет снизить влияние аномальных значений на работу алгоритмов. Кластеры, построенные на основе расстояния Манхэттена, стремятся к кубической форме. Иногда расстояние Манхэттена называют «расстояние городских кварталов» (англ.: city-block distance), из-за ассоциаций, возникающих с прямоугольными формами застройки, которая характерна для современных городов.

3. Сформировать кластеры, для каждого центройда  из множества Х отобрать подмножество точек Хк с минимальным расстоянием до  

Пример.  Для лучшего понимания методики воспользуемся геометрической интерпретацией определения, к какому из центров кластеров ближе всего расположена та или иная запись. Границей между двумя кластерами является точка, равноудаленная от четырех центров. Из геометрии известно, что множество точек, равноудаленных от двух точек A и B, будут образовывать прямую, перпендикулярную отрезку AB и пересекающую его по середине. Принцип поиска границ будущих кластеров поясняется с помощью рисунке. Для простоты рассматривается 2-мерный случай, когда пространство признаков содержит всего два измерения (X1,X2). Пусть на первом шаге были отобраны три точки A, B и C. Тогда линия 1, проходящая перпендикулярно отрезку AB через его середину, будет состоять из точек, равноудаленных от точек A и B. Аналогично строится прямая 2 для точек A и C, а также прямая 3 для точек B и C. 

Используя данные линии можно определить, к какому из центров оказывается ближе та или иная точка.

Однако, такая «геометрическая» интерпретация определения того, в «сферу влияния» какого центра кластера входит та или иная запись, полезна только для лучшего понимания. На практике для этого вычисляется расстояние от каждой записи до каждого центра в многомерном пространстве признаков, и выбирается то «семя», для которого данное расстояние минимально (более подробно это рассмотрено ниже).

4. Вычислить новые центроиды как среднее всех точек кластера Хк

где  - количество точек в кластере К

Например, если в кластер вошли три записи с наборами признаков , то координаты его центроида будут рассчитываться следующим образом:

Затем старый центр кластера смещается в его центроид. На рисунке центры тяжести кластеров представлены в виде крестиков.

Таким образом, центроиды становятся новыми центрами кластеров для следующей итерации.

Шаги 3 и 4 повторяются до тех пор, пока выполнение алгоритма не будет прервано либо не будет выполнено условие в соответствии с некоторым критерием сходимости. 

Остановка алгоритма производится тогда, когда границы кластеров и расположения центроидов не перестанут изменяться от итерации к итерации, т.е. на каждой итерации в каждом кластере будет оставаться один и тот же набор записей. На практике алгоритм k-means обычно находит набор стабильных кластеров за несколько десятков итераций.

Что касается критерия сходимости, то чаще всего используется критерий суммы квадратов ошибок между центроидом кластера и всеми вошедшими в него записями, т.е. 

где - произвольная точка данных, принадлежащая кластеру - центроид данного кластера. Иными словами, алгоритм алгоритм остановится тогда, когда ошибка E достигнет достаточно малого значения.

 Одним из основных недостатков, присущих этому алгоритму, является отсутствие четких критериев выбора числа кластеров, целевой функции их инициализации и модификации. Кроме этого, он является очень чувствительным к шумам и аномальным значениям в данных, поскольку они способны значительно повлиять на среднее значение, используемое при вычислении положений центроидов (см. рис. 1-4).

Чтобы снизить влияние таких факторов, как шумы и аномальные значения, иногда на каждой итерации используют не среднее значение признаков, а их медиану. Данная модификация алгоритма называется k-mediods (k-медиан).

Также можно рассмотреть функцию оценки Q качества работы кластеризатора

 где с - количество кластеров, di - среднее внутрикластерное расстояние, d0 - среднее межкластерное расстояние

Для получения наилучшего результата можно несколько раз выполнить алгоритм кластеризации после чего выбрать результат с наименьшим значением Q.

Свою популярность алгоритм k-means приобрел благодаря следующим свойствам.

Во-первых, это умеренные вычислительные затраты, которые растут линейно с увеличением числа записей исходной выборки данных. Вычислительная сложность алгоритма определяется как k *n *l , где k - число кластеров, n - число записей и l - число итераций. Поскольку k и l заданы, то вычислительные затраты возрастают пропорционально числу записей исходного множества.

Полезным свойством k-means является то, что результаты его работы не зависят от порядка следования записей в исходной выборке, а определяются только выбором исходных точек.

Пример работы алгоритма k-means

Пусть имеется набор из 8 точек данных в двумерном пространстве, из которого требуется получить два кластера. Значения точек приведены в табл. 1 и на рис. 5.

Шаг 1. 

Определим число кластеров, на которое требуется разбить исходное множество k=2.

Шаг 2.

Случайным образом выберем две точки, которые будут начальными центрами кластеров. Пусть это будут точки m1=(1;1) и m2=(2;1). На рис. 5 они закрашены черным цветом

Шаг 3. 

Проход 1.

Для каждой точки определим к ней ближайший центр кластера с помощью расстояния Евклида. В табл. 2 представлены вычисленные с помощью формулы  расстояния между центрами кластеров m1=(1;1), m2=(2;1) и каждой точкой исходного множества, а также указано, к какому кластеру принадлежит та или иная точка.

Таким образом, кластер 1 содержит точки A, E, G, а кластер 2 - точки B, C, D, F, H. Как только определятся члены кластеров, может быть рассчитана сумма квадратичных ошибок:

Шаг 4. 

Проход 1.

Для каждого кластера вычисляется его центроид, и центр кластера перемещается в него.

Центроид для кластера 1:  [(1+1+1)/3, (3+2+1)/3] = (1; 2). 

Центроид для кластера 2: [(3 + 4 + 5 + 4 + 2)/5, (3 + 3 + 3 + 2 + 1)/5] = (3,6; 2,4).

Расположение кластеров и центроидов после первого прохода алгоритма представлено на рис. 6.

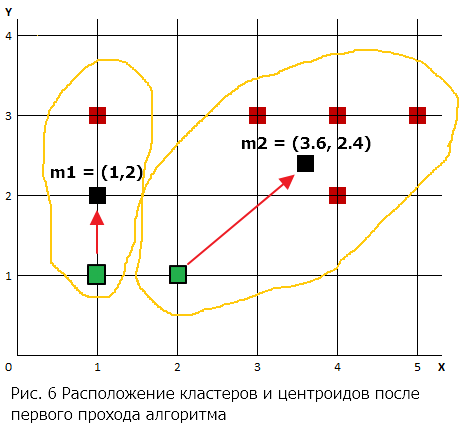
На рис. 6 начальные центры кластеров закрашены зеленым цветом , а центроиды, вычисленные при 1-м проходе алгоритма, - закрашены черным цветом. Они и будут являться новыми центрами кластеров, к которым будет определяться принадлежность точек данных на втором проходе.

Шаг 3.

Проход 2.

После того, как найдены новые центры кластеров, для каждой точки снова определяется ближайший к ней центр и ее отношение к соответствующему кластеру. Для это еще раз вычисляются евклидовы расстояния между точками и центрами кластеров. Результаты вычислений приведены в табл. 3.

Относительно большое изменение m2 привело к тому, что запись H оказалась ближе к центру m1, что автоматически сделало ее членом кластера 1. Все остальные записи остались в тех же кластерах, что и на предыдущем проходе алгоритма. Таким образом, кластер 1 будет A, E, G, H, а кластер 2 - B, C, D, F. Новая сумма квадратов ошибок составит:

,что показывает уменьшение ошибки относительно начального состояния центров кластеров (которая на первом проходе составляла 36). Это говорит об улучшении качества кластеризации,т.е. более высокую «кучность» объектов относительно центра кластера.

Шаг 4.

Проход 2.

Для каждого кластера вновь вычисляется его центроид, и центр кластера перемещается в него.

Новый центроид для 1-го кластера:  [(1+1+1+2)/4, (3+2+1+1)/4]=(1.25, 1.75).

Центроид для кластера 2: [(3 + 4 + 5 + 4)/4, (3 + 3 + 2 + 4)/4] = (4, 2.75).

Расположение кластеров и центроидов после второго прохода алгоритма представлено на рис. 7.

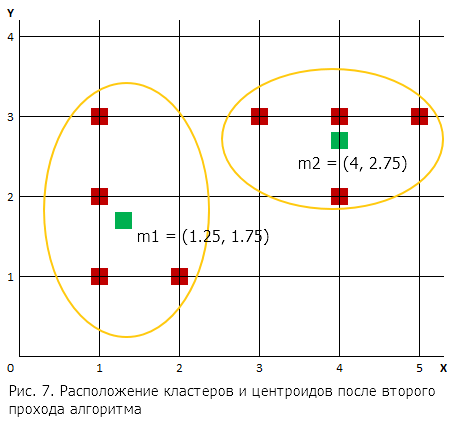
По сравнению предыдущим проходом центры кластеров изменились незначительно.

Шаг 3.

Проход 3.

Для каждой записи вновь ищется ближайший к ней центр кластера. Полученные на данном проходе расстояния представлены в табл. 4.

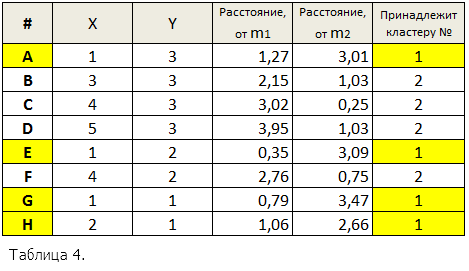
Следует отметить, что записей, сменивших кластер на данном проходе алгоритма, не было. Новая сумма квадратов ошибок составит

Таким образом, изменение суммы квадратов ошибок является незначительным по сравнению с предыдущим проходом.

Шаг 4.

Проход 3.

Для каждого кластера вновь вычисляется его центроид, и центр кластера перемещается в него. Но поскольку на данном проходе ни одна запись не изменила своего членства в кластерах, то положение центроида не поменялось, и алгоритм завершает свою работу.

Итоговое распределение на кластеры смотрите на рис. 7.

Итак, в этой статье  было показано, КАК ПОЛУЧИТЬ ОПТИМАЛЬНЫЕ МАРШРУТЫ ДЛЯ ЗАДАННОГО КОЛИЧЕСТВА А/ТРАНСПОРТА из указанного места отгрузки, при этом грузоподъемность транспорта не принималась во внимание. 

В следущей статье "Метод Кларка-Райта. Оптимальное планирование маршрутов грузоперевозок"  будет показано КАК УЗНАТЬ КОЛИЧЕСТВО НЕОБХОДИМОГО А/ТРАНСПОРТА С УЧЕТОМ ЕГО ГРУЗОПОДЪЕМНОСТИ ДЛЯ ФОРМИРОВАНИЯ ОПТИМАЛЬНЫХ МАРШРУТОВ.

Источник: infostart.ru

Комментарии: