Если вы полагаете, что фундаментальные исследования всегда скучны и с трудом находят применение на практике, то прочитайте эту статью. Старший научный сотрудник нашей лаборатории Сергей Муравьев, занимающийся автоматизацией решения задач кластеризации, рассказывает о собственном проекте, у которого, кажется, есть всё, что только можно пожелать: научная фундаментальность, хитрые задачи на пути к цели, а также впечатляюще широкие возможности применения.
Почему это круто
Кластерный анализ неформально можно определить как разбиение множества объектов так, чтобы похожие объекты попали в одно и то же подмножество, а объекты из разных подмножеств существенно различались. От обычной классификации по заданным признакам кластерный анализ отличается тем, что не алгоритм, а человек выявляет критерий кластеризации данных. Эта задача относится к классу «обучения без учителя» (англ. unsupervised learning), так как размеченного набора данных или какой-то заведомо известной информации о нём не предоставляется.
У задачи кластеризации нет общепризнанного математически корректного определения. Дело в количестве разнообразных применений: в маркетинге для сегментирования целевой аудитории, в медицине для классификации болезней, в рекомендательных системах при организации баз данных для поисковых запросов, при изучении социальной стратификации, для сегментирования изображений и распознавания образов, при обнаружении и сегментации артефактов различных периодов в археологии и много ещё для чего.
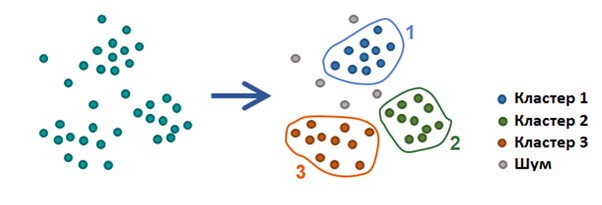
Универсальный алгоритм, который подходит для всех задач, построить невозможно (теорема Клейнберга). Принципиально невозможно найти решения задачи кластеризации, ведь существует множество критериев оценки качества разбиения, а число кластеров обычно неизвестно заранее. Поэтому алгоритмы кластеризации нужно подбирать и настраивать почти для каждой задачи отдельно.
Задача выбора и настройки алгоритма машинного обучения является экспертной, что достаточно затратно по времени, поскольку работа выполняется человеком фактически вручную. Автоматизация подбора и настройки алгоритмов кластеризации экономит множество интеллектуальных, временных и других ресурсов в разных областях применения кластерного анализа. Система, которая могла бы автоматически рекомендовать и настраивать подходящий алгоритм кластеризации для каждой задачи в отдельности, была бы весьма актуальна.
Как определить меру качества
Ключевая сложность, с которой пришлось столкнуться в процессе исследования, состояла в том, чтобы понять, как корректно подобрать меру качества, по которому сравниваются возможные решения. Эту сложность получилось преодолеть с помощью рекомендации меры качества разбиения для каждой задачи на основе принципа мета-обучения.
Основная идея мета-обучения состоит в сведении задачи выбора алгоритма к задаче обучения с учителем: задачи описываются мета-признаками, характеризующими свойства решаемой задачи, при этом агрегированные сведения о работе алгоритмов (лучший алгоритм, ранжирование над алгоритмами и т.д.) выступают целевой функцией в такой постановке. Это может быть как сам алгоритм, так и оценка его работы на конкретной задаче по какой-либо мере.
Таким образом удалось разработать методологию визуальной оценки мер на основе визуальной оценки разбиений и сведении задачи предсказания такой оценки для новых наборов данных к задаче классификации в пространстве мета-признаков, описывающих поставленную задачу кластеризации. Далее расскажу об этом подробнее.
Сравниваем разбиения
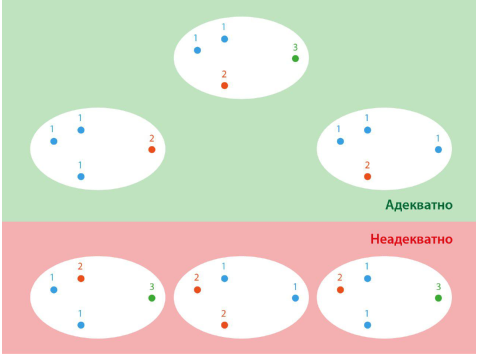
Берём алгоритмы кластеризации и применяем их к набору данных. Полученные разбиения можно оценивать как адекватные или неадекватные, а ещё можно проводить сравнения разбиений друг с другом, чтобы определить лучшие. На рисунке ниже приведён пример сравнения различных разбиений примитивного набора данных с точки зрения адекватности, а также с точки зрения сравнения разбиений друг с другом. Чем выше на рисунке расположено разбиение, тем оно лучше с точки зрения попарного сравнения с другими разбиениями.
Сравниваем меры качества
Основываясь на критериях оценки качества кластеризации с точки зрения визуального восприятия, я ввёл два критерия мер качества — критерий адекватности и критерий ранжирования.
Критерий адекватности меры — оценка адекватности лучшего разбиения заданного набора данных с точки зрения визуального восприятия.
Критерий ранжирования — нормированная функция расстояния между ранжированием разбиений, задаваемым мерой качества, и агрегированным ранжированием разбиений, задаваемым оценками на основе визуального восприятия. Область значения данной функции:
чем значение функции ближе к
, тем рассматриваемая мера качества лучше.
Для наглядности давайте рассмотрим пример с собранным мною набором данных из двухсот двумерных наборов данных 2D-200. Для каждого набора данных из 2D-200 были сформированы 14 разбиений. Эти разбиения были оценены пятью асессорами и девятнадцатью мерами качества. В итоге на наборе данных 2D-200 выявлены лучшие меры качества с точки зрения критериев и
Затем для каждой меры по всем элементам из 2D-200 были вычислены следующие величины:
— соотношение числа раз, когда мера отвечала критерию адекватности
к общему числу экспериментов;
— соотношение числа раз, когда мера была лучшей с точки зрения критерия ранжирования
к общему числу экспериментов.
Значения и
для всех мер качества на наборе данных наборов данных 2D-200 представлены в таблице ниже.
Мера | | | Мера |
|
|
DB |
|
| Sym |
|
|
Dunn |
|
| CI |
|
|
Silhouette |
|
| DB* |
|
|
CH |
|
| gD31 |
|
|
S_Dbw |
|
| gD41 |
|
|
SymDB |
|
| gD51 |
|
|
CS |
|
| gD33 |
|
|
COP |
|
| gD43 |
|
|
SV |
|
| gD53 |
|
|
OS |
|
|
Из таблицы видно, что ни одна рассмотренная мера не претендует на универсальность по введенным критериям, а значит, меру качества нужно рекомендовать для каждого набора данных отдельно.
Однако эффективная рекомендация из девятнадцати мер качества требует значительно большего числа наборов данных, чем представлено в 2D-200. Поэтому я построил множество из четырех самых лучших мер с точки зрения — среднего значения, вычисляемого на основе критерия ранжирования мер: мера Silhouette, мера Calinski-Harabasz, мера gD41 и мера OS. В таблице приведены значения
для всех исследованных мной внутренних мер качества.
Мера |
| Мера |
|
gD41 |
| gD53 |
|
gD43 |
| S_Dbw |
|
gD33 |
| Dunn |
|
OS |
| gD51 |
|
CH |
| CI |
|
Silhouette |
| CS |
|
SV |
| DB |
|
Sym |
| COP |
|
gD31 |
| DB* |
|
SymDB |
|
Классификатор, который рекомендует меру качества
Всякий раз производить данные вычисления довольно ресурсозатратно. Можно упростить задачу рекомендации меры качества, если свести её к задаче классификации. И я решил построить классификатор, который для нового набора данных предсказывает, какая из рассматриваемых мер качества будет лучше с точки зрения агрегированных оценок асессоров, если бы они действительно проходили описанный выше тест для этого набора данных. В качестве классификатора я использовал алгоритм случайного леса, который выбрал экспериментально, и который показывает качество классификации Интересно, что разработанный мета-классификатор сам по себе выступает новой мерой качества, назовём её Meta-CVI.
Как подобрать алгоритм
После того как мера качества известна, я определил два способа получения конечного разбиения, а именно построение эвристического или эволюционного алгоритмов кластеризации. В эвристических алгоритмах содержится неизменяемый критерий качества выстраиваемого разбиения, в эволюционных же критерий качества является гиперпараметром алгоритма. Гиперпараметры — это параметры, значения которых задаются до начала обучения, не изменяются в процессе обучения и не зависят от заданного набора данных. Примерами эвристических алгоритмов служат такие алгоритмы, как k-Means, иерархический алгоритм и DBSCAN. Эволюционные алгоритмы осуществляют непосредственный поиск в пространстве возможных разбиений с целью найти оптимальное по задаваемой в качестве параметра мере качества.
Эвристические алгоритмы
Проблема в том, что заранее невозможно предсказать, насколько качественное разбиение построит тот или иной алгоритм. Если уделять равное время настройке всех возможных для данной задачи алгоритмов, то получится, что большая часть времени при такой схеме будет потрачена на настройку заведомо неэффективных алгоритмов. Но если сосредоточиться лишь на одном алгоритме, то часть из тех, что могли бы обеспечить лучшее качество кластеризации, не будут рассматриваться.
Чтобы решить эту проблему, я разработал метод выбора и настройки алгоритмов на базе обучения с подкреплением MASSCAH. Этот метод сводится к задаче о многоруком бандите. Предлагается осуществлять поиск компромисса между исследованием и эксплуатацией процессов настройки параметров для различных алгоритмов кластеризации.
В задаче о многоруком бандите рассматривается агент, тянущий за ручки тотализатора, с каждой из которых связано некоторое неизвестное распределение награды. Каждый ход агент выбирает ручку и получает случайную награду из связанного с ней распределения. Цель агента — максимизировать полученную за несколько итераций награду.
Давайте формализуем задачу. Пусть задан некоторый временной бюджет на поиск лучшего алгоритма
Требуется разбить его на интервалы
таким образом, что при запуске процессов
с ограничением по времени
получается значение меры качества
такое, что:
гдеи
В этом случае каждой ручке бандита соответствует определённая модель алгоритма кластеризации из конечного множества вызову ручки
на итерации
— процесс оптимизации гиперпараметров этой модели в течение времени
В результате будет достигнуто качество кластеризации
Качество кластеризации определяется с помощью меры, оно и задает награду, получаемую по завершении итерации.
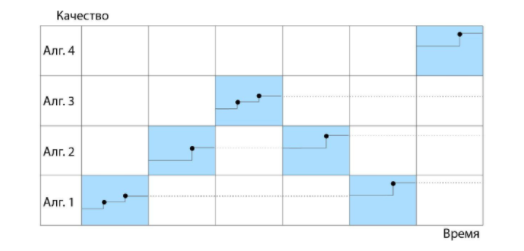
Иллюстрация работы метода выбора и настройки эвристического алгоритма MASSCAH представлена на рисунке ниже:

Эволюционные алгоритмы
Одним из ключевых аспектов работы эволюционных алгоритмов является вычисление функции приспособленности. В нашем случае — это внутренняя мера оценки разбиения. Важно научиться быстро её перерасчитывать, если структура кластеров изменилась. Переформулировать задачу можно так: пусть точка переместилась из кластера
в кластер
Каким образом можно инкрементально (то есть соответственно каждой новой конфигурации кластеров) перечитывать значение меры вместо того, чтобы вычислять его заново? Поскольку не для всех мер возможен точный инкрементальный перерасчёт за время, меньшее чем полный пересчет, я пересчитывал значение меры приблизительно, когда это невозможно сделать точно.
Основная идея состоит в том, чтобы сохранить большинство подсчитанных расстояний между элементами набора данных или расстояний между центроидами кластеров и элементами набора данных. Большинство внутренних мер качества разбиений используют расстояния между элементами, а также расстояния между элементами и центроидами кластеров. Объекты обычно описываются некоторым -мерным векторным пространством. Соответственно, центроидом кластера будет являться центр масс объектов в векторном пространстве, входящих в кластер. В таблице приведены сложностные оценки для полного и инкрементального подсчёта девятнадцати используемых в исследовании внутренних мер. Из таблицы видно, что асимптотическая сложность инкрементального пересчёта всех внутренних мер лучше, чем полный их пересчёт.
Мера | Полный пересчёт | Инкрементальный пересчёт | Точность пересчёта |
Dunn |
|
| точный пересчёт |
CH |
|
| аппроксимация |
CI |
|
| аппроксимация |
DB |
|
| аппроксимация |
Sil |
|
| точный пересчёт |
gD31 |
|
| точный пересчёт |
gD33 |
|
| аппроксимация |
gD41 |
|
| аппроксимация |
gD43 |
|
| аппроксимация |
gD51 |
|
| аппроксимация |
gD53 |
|
| аппроксимация |
CS |
|
| аппроксимация |
DB* |
|
| аппроксимация |
Sym |
|
| аппроксимация |
SymDB |
|
| аппроксимация |
COP |
|
| аппроксимация |
SV |
|
| аппроксимация |
OS |
|
| аппроксимация |
S_Dbw |
|
| аппроксимация |
Для эволюционных алгоритмов важен выбор стратегии, операций кроссовера и мутаций на каждой итерации. Анализируя работы различных эволюционных алгоритмов, я выяснил, что качество получаемого разбиения зависит в основном от выбираемых мутаций. Поэтому из нескольких тестируемых решил использовать самую эффективную по временистратегию, в которой на каждой итерации равновероятно выбирается одна из мутаций. Таким образом, нужно проводить лишь настройку
стратегии, а именно — выбор используемых мутаций для решаемой задачи кластеризации.

Принимая во внимание эту особенность, я придумал мета-классификатор, рекомендующий список мутаций для решаемой задачи кластеризации. По всем запускам алгоритма с равновероятно выбираемыми мутациями для каждого из используемых набора данных я посчитал степень «полезности» каждой мутации. Для каждого запуска алгоритма построил распределение, которое показывало, какое число раз та или иная мутация давала прирост с точки зрения функции приспособленности на каждой итерации. Потом я взял пять лучших мутаций и построил бинарный вектор, где лучшим мутациям соответствовала а остальным —
. Мета-признаковое описание каждого набора данных аналогично тому, которое использовалось мной для построения классификатора, предсказывающего меру качества. Таким образом был построен мета-классификатор, позволяющий для каждого набора данных рекомендовать набор мутаций, который нужно использовать в
алгоритме.
Ниже представлена таблица числа запусков алгоритма с автоматизацией и без неё, сгруппированная по оптимизируемым мерам качества. «Хуже» и «не хуже» означает, что автоматизированный алгоритм, соответственно, отстаёт либо не отстаёт от алгоритма без автоматической настройки параметров по качеству разбиений;
— среднее время работы алгоритма с автоматизацией и без неё соответственно.
Calinski-Harabasz | OS | gD41 | Silhouette | |||||
хуже | не хуже | хуже | не хуже | хуже | не хуже | хуже | не хуже | |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
Сравнение алгоритмов
Интересно сравнить алгоритм на основе выбора и настройки эвристических алгоритмов кластеризации MASSCAH с алгоритмом настройки эволюционного алгоритма кластеризации.
Я предположил, что два алгоритма получают одинаковые значения меры качества, если интервалы этих значений пересекаются. То есть была использована квантиль уровня
для нормального распределения. Временной бюджет алгоритма, запускаемого на определённых мере и наборе данных, задавался равным среднему времени работы автоматизированного эволюционного алгоритма на этих мере и наборе данных. Я запустил алгоритмы со всеми отобранными ранее четырьмя мерами качества: Silhouette, Calinski-Harabasz, gD41 и OS. Для каждой пары «мера – набор данных» производилось 10 запусков алгоритма. Полученные количества удачных и неудачных запусков приведены в таблице ниже.
Число положительных и отрицательных результатов сравнений алгоритмов на базе метода выбора и настройки эвристического алгоритма кластеризации на основе обучения с подкреплением, сгруппированные по мере качества разбиений. Столбец MASSCAH > Evo соответствует случаям, когда качество эволюционного алгоритма оказалось хуже, чем алгоритма на базе обучения с подкрепление, MASSCAH ? Evo — что качества сравнимы, MASSCAH < Evo — разработанный алгоритм опережает существующий результат.
| | |
| |
Мера CH |
|
|
|
Мера OS |
|
|
|
Мера Silhouette |
|
|
|
Мера gD41 |
|
|
|
Все меры |
|
|
|
Мера Meta-CVI |
|
|
|
Можно заметить, что успешность эволюционного алгоритма зависит от используемой меры, но по общему числу запусков он сравним с предложенным методом выбора и настройки гиперпараметров эвристического алгоритма кластеризации. Отдельно стоит заметить, что эволюционный алгоритм кластеризации с автоматически настраиваемыми параметрами опережает таковой без автоматической настройки параметров по измеренным характеристикам независимо от меры, однако при этом его производительность по сравнению с разработанным методом на основе обучения с подкреплением зависит от выбора меры оценки качества разбиения. Кроме того, расчёт числа удачных и неудачных запусков производился для предложенной мной меры Meta-CVI.
Как применить всё это на практике
После того как была определена мера качества, построены и оценены алгоритмы кластеризации, я решил объединить всё это в систему и разработать такой программный комплекс, который бы реализовал данные алгоритмы и позволял осуществлять оптимальное разбиение для данной задачи по выбранной мере качества.
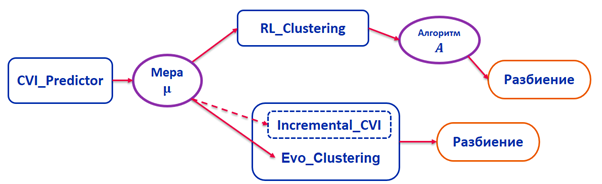
Этот программный комплекс состоит из нескольких пакетов. Пакет CVI_Predictor реализует алгоритм предсказания меры для конкретной задачи кластеризации на основе мета-обучения. Пакет RL_Clustering реализует различные алгоритмы на базе представленного в работе метода выбора и настройки эвристического алгоритма кластеризации. Пакет Evo_Clustering реализует эволюционный алгоритм кластеризации с параметрами, настраиваемыми при помощи мета-обучения. Пакет Incremental_CVI реализует инкрементальное вычисление мер качества разбиений. Весь комплекс можно скачать на GitHub.
Разработанную система автоматического выбора и оценки алгоритмов кластеризации и их параметров я защитил в рамках своей кандидатской диссертации в декабре 2019 года. Автореферат и диссертацию можно почитать здесь.
На сегодняшний день система автоматического выбора и оценки алгоритмов кластеризации и их параметров была успешно использована в рамках государственного задания №2.8866.2017/8.9 «Технология разработки программного обеспечения систем управления ответственными объектами на основе глубокого обучения и конечных автоматов». В рамках этого задания решалась задача нахождения формальной грамматики по некоторому конечному списку слов, которые принадлежат некоторому неизвестному формальному языку. В частности, была решена важная подзадача разметки «слов-примеров», по которым строится грамматика при помощи рекуррентных нейронных сетей.
Также система использовалась в рамках проекта компании Statanly для разработки алгоритма поиска документов ограниченного размера. В частности, решалась задача оценки кластеризации векторных представлений слов. Для этого использовался корпус русских слов Тайга.
Помимо этого, программный комплекс был применён для разработки рекомендательной системы выбора научного руководителя и темы исследования для абитуриентов Университета ИТМО.
В планах — разработка полноценной библиотеки, реализующей алгоритмы выбора и оценки алгоритмов кластеризации и их параметров. Кроме того, в будущем планируется дальнейшее исследование задачи кластеризации, а именно вопросов кластеризуемости наборов данных, описывающих каждую задачу. И я был бы рад пополнению в наших рядах сильных в техническом плане и амбициозных студентов.