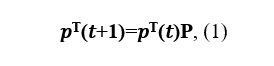PAGERANK: алгоритм ранжирования WEB-страниц

Итак, рассмотрим ориентированный взвешенный граф. Пусть у графа n вершин. Каждой паре вершин соответствует некоторый вес (вероятность перехода).

Стоит отметить, что типичные web-графы – это однородная дискретная марковская цепь, для которой выполняется условие неразложимости и условие апериодичности. Запишем уравнение Колмогорова-Чэпмена: где P – переходная матрица.

Предположим, что существует предел

Вектор v называют стационарным распределением вероятности.

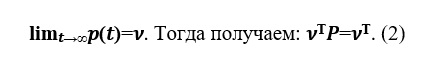
Именно из соотношения (2) и было предложено искать вектор ранжирования web-страниц в модели Брина-Пейджа.

Так как v является пределом

то стационарное распределение можно вычислить методом простых итераций (МПИ).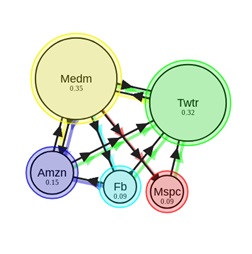

Для того чтобы перейти с одной web-страницы на другую, пользователь должен с определенной вероятностью выбрать, по какой именно ссылке перейти. В случае если у документа несколько исходящих ссылок, то будем считать, что пользователь переходит по каждой из них с одинаковой вероятностью. Ну и, наконец, есть еще коэффициент телепортации, который показывает нам, что с какой-то вероятностью пользователь может с текущего документа переместиться на другую страницу, не обязательно связанную напрямую со страницей, в которой мы находимся в данный момент. Пусть пользователь телепортируется с вероятностью ?, тогда, уравнение (1) примет вид

При 0 < ? < 1 уравнение гарантированно имеет единственное решение. На практике для вычисления PageRank обычно используют уравнение с ? = 0,15. Рассмотрим web-граф Google с сайта — ссылка. Данный web-граф содержит 875713 вершин, а это значит, что для двумерной матрицы P нужно выделить 714 Gb памяти. Оперативная память современных компьютеров на порядок меньше, поэтому компьютер начинает задействовать память жесткого диска, обращение к которой сильно замедляет работу программы вычисления PageRank. Но матрица P является разреженной матрицей — матрица с преимущественно нулевыми элементами. Для работы с разреженными матрицами в Python используется модуль sparse из библиотеки scipy, которая помогает матрице P занимать гораздо меньше памяти.

Применим данный алгоритм на этих данных. Узлы представляют собой веб-страницы, а направленные ребра-гиперссылки между ними. Для начала импортируем нужные нам библиотеки:

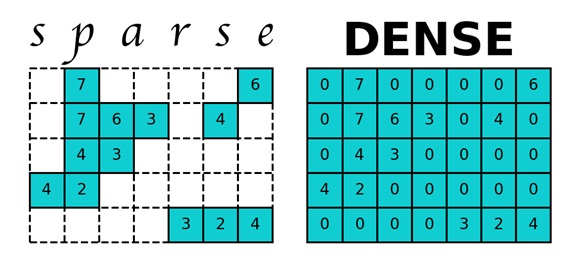
import cvxpy as cp import numpy as np import pandas as pd import time import numpy.linalg as ln from scipy.sparse import csr_matrix

Теперь перейдем к самой реализации:

#считываем данные с файла data = pd.read_csv("web-Google.txt", names = ['i','j'], sep="	", header=None) NODES = 916428 EDGES = 5105039 #представление разреженной матрицы NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES)) b = NEW.sum(axis=1) NEW = NEW.transpose() #начальные параметры p0 = np.ones((NODES,1))/NODES eps = 10**-5 delta = 0.15  ERROR = True k = 0 #сам алгоритм while (ERROR == True):     with np.errstate(divide='ignore'):               z = p0 / b     p1 = (1-delta) * NEW.dot(csr_matrix(z)) + delta * np.ones((NODES,1))/NODES     if (ln.norm(p1-p0) < eps):         ERROR = False     k = k + 1 #обновляем вектор  PageRank     p0 = p1 

На графиках можем видеть, как вектор p приходит к стационарному состоянию v:

С помощью вектора PageRank можно так же определять победителя на выборах. Небольшая часть участников Википедии-это администраторы, которые являются пользователями с доступом к дополнительным техническим функциям, помогающим в обслуживании. Для того, чтобы пользователь стал администратором, выдается запрос на администраторство, и сообщество Википедии посредством публичного обсуждения или голосования решает, кого продвигать на должность администратора. Задачу PageRank так же можно свести к задаче минимизации и решить с помощью метода условного градиента Франка–Вульфа, который заключается в следующем: выбираем одну из вершин симплекса и делаем точку старта в этой вершине. Реализация данного метода на данных — ссылка представлена ниже:

#считываем данные с файла data = pd.read_csv("grad.txt", names = ['i','j'], sep="	", header=None) NODES = 6301 EDGES = 20777 #представление разреженной матрицы NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES)) b = NEW.sum(axis=1) NEW = NEW.transpose() e = np.ones(NODES) with np.errstate(divide='ignore'):               z = e / b NEW = NEW.dot(csr_matrix(z))  #начальные параметры eps = 0.05 k=0 a_0 = 1 y = np.zeros((NODES,1)) p0 = np.ones((NODES,1))/NODES #первая итерация p0[0] = 0.1 y[np.argmin(df(p0))] = 1                p1 = (1-2/(1+k))*p0 + 2/(1+k)*y #последующие итерации while ((ln.norm(p1-p0) > eps)):         y = np.zeros((NODES,1))         k = k + 1         p0 = p1         y[np.argmin(df(p0))] = 1             p1 = (1-2/(1+k))*p0 + 2/(1+k)*y

Для эффективной работы реальной поисковой системы скорость вычисления вектора PageRank оказывается важнее точности его вычисления. МПИ не позволяет пожертвовать точностью в угоду скорости вычисления. Алгоритм Монте-Карло помогает в какой-то мере справиться с этой проблемой. Мы запускаем виртуального пользователя, который блуждает по страницам сайтам. Собирая статистику посещения им страниц сайта, спустя достаточно большой промежуток времени мы получаем для каждой страницы, сколько раз на ней был пользователь. Нормируя этот вектор, мы получаем искомый вектор PageRank. Продемонстрируем работу этого алгоритма на уже используемых данных.

#функция для случайного прохода по вершинам графа def get_edges(m, i):     if (i == NODES):         return random.randint(0, NODES)     else:         if (len(m.indices[m.indptr[i] : m.indptr[i+1]]) != 0):             return np.random.choice(m.indices[m.indptr[i] : m.indptr[i+1]])         else:             return NODES #считываем данные с файла        data = pd.read_csv("web-Google.txt", names = ['i','j'], sep="	", header=None) NODES = 916428 EDGES = 5105039  NEW = csr_matrix((np.ones(len(data['i'])),(data['i'],data['j'])),shape=(NODES,NODES)) #cам алгоритм, total – количество блужданий for total in range(1000000,2000000,100000): #начальные параметры     k = random.randint(0, NODES) #переменная для хранения PageRank     ans = np.zeros(NODES+1)     margin2 = np.zeros(NODES)     ans_prev = np.zeros(NODES)     for t in range(total):         j = get_edges(NEW, k)         ans[j] = ans[j]+1         k = j #удаляем введенную раньше для телепортации искусственную вершину      ans = np.delete(ans, len(ans)-1)     ans = ans/sum(ans)     for number in range(len(ans)):         margin2[number] = ans[number] - ans_prev[number]     ans_prev = ans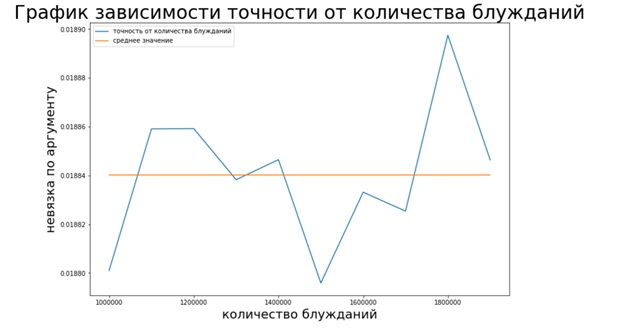

Как видно из графика метод Монте-Карло в отличие от двух предыдущих методов не является стабильным (отсутствует сходимость), однако он помогает оценить вектор Page Rank, не требуя на это много времени. Вывод: Таким образом, мы рассмотрели основные алгоритмы определения PageRank web-графов. Перед началом проектирования сайта стоит убедиться, что PageRank не растрачивается впустую, для этого стоит уделить внимание следующим вещам:

1. Внутренние ссылки показывают на то, как “ссылочный вес” аккумулирует на вашем сайте, поэтому сосредоточьте важную информацию на главной странице сайта, так как наверняка “главная” страница сайта обладает наиболее сильным PageRank.
2. Страницы-“сироты”, на которых нет ссылок с других страниц вашего сайта. Стараться избегать таких страниц.
3. Стоит указывать внешние ссылки, если от них есть польза для посетителя вашего сайта.
4. Битые внешние ссылки размывают общий вес страницы, поэтому необходимо периодически следить за ними и “чинить” при надобности.

Однако, это не означает, что вы должны зацикливаться на PageRank. Но, стоит помнить, что, обращая внимание на структуру сайта при его построении, особенности внутренних и внешних ссылок, вы оптимизируете сайт под PageRank.